2022-2023学年北师大版七年级数学下册 第四章 三角形期末单元自测题(含答案)
文档属性
| 名称 | 2022-2023学年北师大版七年级数学下册 第四章 三角形期末单元自测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 560.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 10:56:52 | ||
图片预览




文档简介
北师大版七年级数学下册 第四章 三角形 单元自测题
一、单选题
1.现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )
A.10cm B.30cm C.50cm D.70cm
2.某同学把三角形的玻璃打碎成了3块,现要到玻璃店配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去
C.带③去 D.①②③都带去
3.有下列两种图示均表示三角形分类,则正确的是( )
A.①对,②不对 B.②对,①不对
C.①、②都不对 D.①、②都对
4.画的边上的高,正确的是( )
A. B.
C. D.
5.如图,下列各组条件中,不能得到的是( )
A., B.,
C., D.,
6.如图,的两条角平分线,交于点P,若,则为( )
A.112° B.115° C.120° D.125°
7.如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )
A.当∠P=60°时,α=30° B.当∠P=60°时,β=40°
C.当=20°时,∠P=90° D.当β=0°时,∠P=90°
8.如图,点B、E、C、F四点共线,∠B =∠DEF,BE = CF,添加一个条件,不能判定 △ABC ≌ △DEF的是( )
A.∠A=∠D B.AB=DE C.AC∥DF D.AC=DF
9.如图,为了估计一池塘岸边两点A,B之间的距离,小丽同学在池塘一侧选取了一点P,测得PA=5m,PB=4m,那么点A与点B之间的距离不可能是( )
A.6.5m B.7.5m C.8.5m D.9.5m
10.已知下列条件,不能作出唯一三角形的是( )
A.两边及其夹角 B.两角及其夹边
C.三边 D.两边及除夹角外的另一个角
二、填空题
11.在中,若,,则是 三角形.(填“锐角”、“直角”、或“钝角”)
12.如图,有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接并延长到D,使,连接并延长到E,使,连接.经测量,,的长度分别为,,,则A,B之间的距离为 m;
13.若a,b,c是三角形的三边长,化简: .
14.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是 .
三、作图题
15.如图,在7×7正方形网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,点A、B都为格点,请分别仅用一把无刻度的直尺在所给的网格中画图,保留画图过程的痕迹.
(1)在如图1中找一格点C,画一条线段AB的平行线段CD;
(2)在图2中找一格点E,画出三角形ABE,使得S△ABE=4.
四、解答题
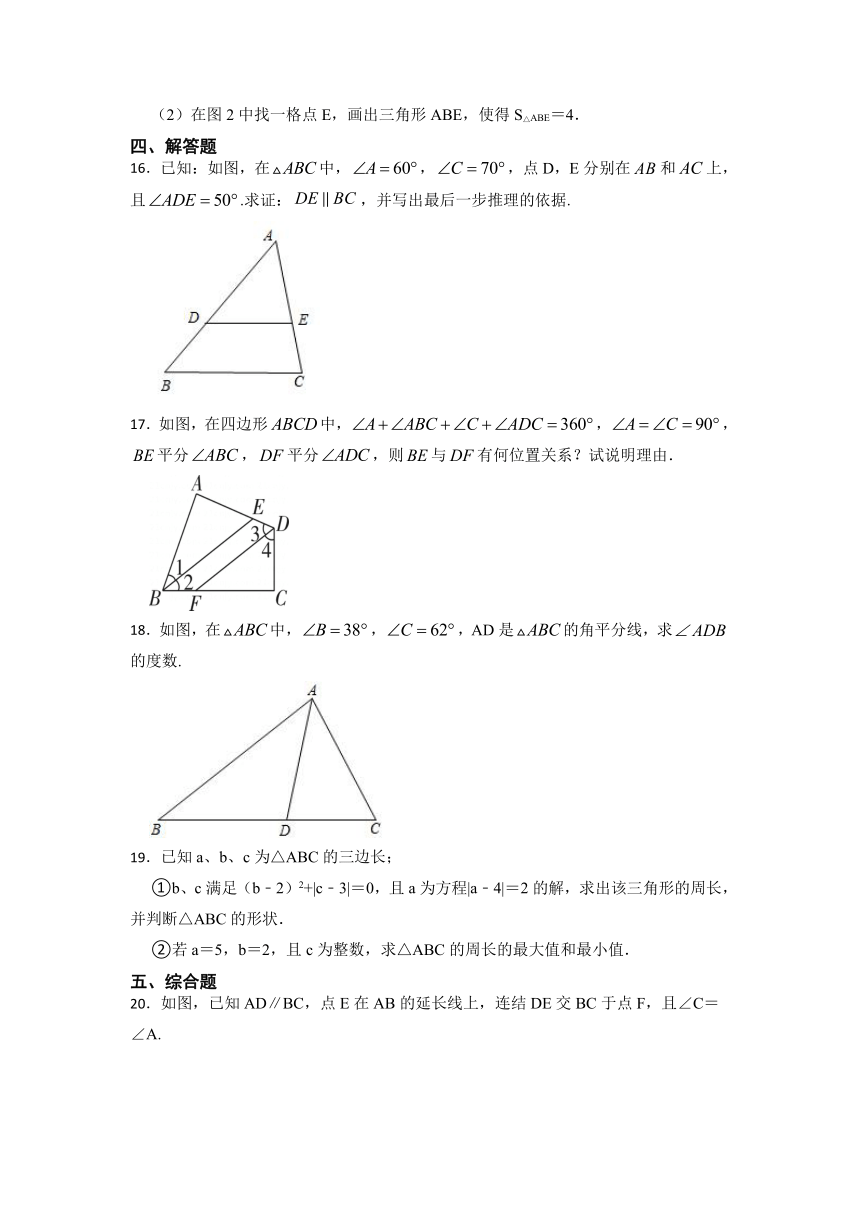
16.已知:如图,在中,,,点D,E分别在和上,且.求证:,并写出最后一步推理的依据.
17.如图,在四边形中,,,平分,平分,则与有何位置关系?试说明理由.
18.如图,在中,,,AD是的角平分线,求的度数.
19.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
五、综合题
20.如图,已知AD∥BC,点E在AB的延长线上,连结DE交BC于点F,且∠C=∠A.
(1)请说明∠E=∠CDE的理由;
(2)若∠1=75°,∠E=30°,求∠A的度数.
21.如图,已知,点A在MN上,点B、C在GH上.在△ABC中,∠ACB=90°,∠BAC=45°.点D、E在直线AB上,在△DEF中,∠DFE=90°,∠EDF=30°.
(1)图中∠BAN的度数是 °;
(2)将△DEF沿直线AB平移,如图2所示,当点F在MN上时,求∠AFE的度数;
(3)将△DEF沿直线AB平移,当以A、D、F为顶点的三角形中,有两个角相等时,请直接写出∠FAN的度数.
22.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合。
(1) 求证:△ADC≌△CEB;
(2) 求两堵木墙之间的距离。
23.已知BM、CN分别是△的两个外角的角平分线,、分别是 和的角平分线,如图①;、分别是和的三等分线(即,),如图②;依此画图,、分别是和的n等分线(即,),且为整数.
(1)若70°,求的度数;
(2)设,请用和n的代数式表示的大小,并写出表示的过程;
(3)当时,请直接写出+与的数量关系.
答案解析
1.【答案】B
【解析】【解答】解:根据三角形的三边关系,得
第三根木棒的长度应大于30-20=10(cm),而小于30+20=50(cm).
故答案为:B.
根据三角形三边关系定理可得“两边之差<第三边<两边之和”可得第三边的范围:10<第三边<50,然后根据各选项即可判断求解.
2.【答案】C
【解析】【解答】解:第①块只保留了原三角形的一个角和部分边,根据这块不能配一块与原来完全一样的;
第②块只保留了原三角形的部分边,根据这两块中的任意一块均不能配一块与原来完全一样的;
第③块不仅保留了原三角形的两个角还保留了一边,则可根据来配一块与原来一样的玻璃.
故答案为:C.
由于③保留两角一边,根据ASA可得全等三角形.
3.【答案】B
【解析】【解答】等腰三角形包括等边三角形,故①的分类不符合题意;图②中的三角形的分类符合题意.
故答案为:B.
根据三角形的分类求解即可。
4.【答案】A
【解析】【解答】解:画△ABC的BC边上的高,即过点A作BC边的垂线.
∴只有选项A符合题意,
故答案为:A.
根据高的定义逐项判断即可。
5.【答案】D
【解析】【解答】解:A、由,,AB=AB,满足SAS能证明,故A不符合题意;
B、,,AB=AB,满足SSS能证明,故B不符合题意;
C、,,AB=AB,满足SAS能证明,故C不符合题意;
D、,,AB=AB,满足SSA,不能证明,故D符合题意;
故答案为:D.
利用全等三角形的判定方法逐项判断即可。
6.【答案】B
【解析】【解答】解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
又∵BD、CE是△ABC的角平分线,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=×130°=65°,
∴∠BPC=180°-65°=115°.
故答案为:B.
根据角平分线的定义可得∠PBC+∠PCB=(∠ABC+∠ACB)=×130°=65°,再利用三角形的内角和求出∠BPC=180°-65°=115°即可。
7.【答案】B
【解析】【解答】解:∵∠ACP=2∠PCD=40°,
∴∠PCD=20°,
∴∠ACD=∠ACP+∠PCD=60°.
∵AB∥CD,
∴∠CAB=180°-∠ACD=120°.
∵∠BAP=α,∠CAP=α+β,
∴∠CAB=2α+β,
∴2α+β=120°,
∴α+β=120°-α,β=120°-2α.
∵∠P+∠CAP+∠ACP=180°,
∴∠P=180°-(α+β+40°)=140°-(α+β)=140°-(120°-α)=20°+α.
当∠P=60°时,20°+α=60°,此时α=40°,故A错误,B正确;
当β=20°时,120°-2α=20°,此时α=50°,
∴∠P=20°+α=70°,故C错误;
当β=0°时,120°-2α=0°,此时α=60°,
∴∠P=20°+α=80°,故D错误.
故答案为:B.
由已知条件可得∠PCD=20°,则∠ACD=∠ACP+∠PCD=60°,根据平行线的性质可得∠CAB=180°-∠ACD=120°,由角的和差关系可得∠CAB=2α+β,则2α+β=120°,进而可得α+β=120°-α,β=120°-2α,由内角和定理可得∠P=20°+α,据此判断.
8.【答案】D
【解析】【解答】解:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
A.∠A=∠D,∠B=∠DEF,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;
B.AB=DE,∠B=∠DEF,BC=EF,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
C.∵AC∥DF,∴∠ACB=∠F,
∠B=∠DEF,BC=EF,∠ACB=∠F,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
D.AC=DF,BC=EF,∠B=∠DEF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
故答案为:D.
根据题意先求出BC=EF,再利用全等三角形的判定方法对每个选项一一判断即可。
9.【答案】D
【解析】【解答】解:∵PA、PB、AB能构成三角形,
∴PA﹣PB<AB<PA+PB,即1m<AB<9m,故D正确.
故答案为:D.
三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出AB的范围,进而判断.
10.【答案】D
【解析】【解答】解:A、B、C分别符合全等三角形的判定SAS、ASA、SSS,故能作出唯一三角形;
D、已知两边及除夹角外的另一个角,不能作出唯一三角形,如等腰三角形底边上的任一点与顶点之间的线段两侧的三角形,错误;
故选D.
看是否符合所学的全等的公理或定理即可.
11.【答案】直角
【解析】【解答】解:∵,
∴,
设,则,根据题意得:
,
解得:,
则,
∴是直角三角形.
故答案为:直角.
先利用三角形的内角和及求出三角形的三个内角,再判断即可。
12.【答案】800
【解析】【解答】解:在△ABC和△EDC中,
∴△ABC≌△EDC(SAS),
∴AB=DE=800.
故答案为:800.
利用“SAS”证明△ABC≌△EDC,再利用全等三角形的性质可得AB=DE=800。
13.【答案】2c-2b
【解析】【解答】解:∵a,b,c是三角形的三边长,
∴,
∴
,
故答案为:2c-2b.
根据三角形三边关系定理“三角形任意两边之和大于第三边”可得a+c>b,a+b>c,于是可得a+c-b>0,c-a-b<0,然后根据绝对值的非负性可去绝对值求解.
14.【答案】2
【解析】【解答】解:∵FC∥AB,
∴∠A=∠ECF,
又∵∠AEC=∠CEF,
在△AED和△CEF中,
,
∴△AED≌△CEF(ASA),
∴AD=CF=5,
∴BD=AD-AB=5-3=2.
故答案为:2.
根据平行线的性质得出∠A=∠ECF,根据对顶角相等得出∠AEC=∠CEF,再利用ASA证明△AED≌△CEF,得出AD=CF=5,最后根据线段和差求BD长即可.
15.【答案】(1)解:如图,线段CD即为所求;
(2)解:如图,△ABE即为所求.
【解析】(1)根据题意作图即可;
(2)根据题意作三角形即可。
16.【答案】证明:∵在中,,,
∴,
∵,
∴,
∴(同位角相等,两直线平行).
【解析】利用三角形内角和定理求出∠B=50°,即得∠B=∠ADE,根据同位角相等,两直线平行即证结论.
17.【答案】结论:BE和DF的位置关系时平行
证明:∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABC=2∠2,∠ADC=2∠4,
∴2∠2+2∠4=180°,
∴∠2+∠4=90°,
∵∠4+∠DFC=90°,
∴∠2=∠DFC,
∴BE∥DF
【解析】利用已知可知∠ABC+∠ADC=180°,利用角平分线的性质可推出∠ABC=2∠2,∠ADC=2∠4,由此可证得∠2+∠4=90°,利用三角形的内角和定理可证得∠4+∠DFC=90°,利用余角的性质可得到∠2=∠DFC,利用同位角相等,两直线平行,可证得结论.
18.【答案】解:在中,(三角形内角和定理).
∵,(已知),
∴(等式的性质).
∵AD平分(已知),
∴(角平分线的定义).
在中,(三角形内角和定理).
∵(已知),(已证),
∴(等式的性质).
【解析】根据三角形的内角和定理算出∠BAC的度数,由角平分线定义算出∠BAD的度数,再由三角形内角和定理算出∠ADB的度数.
19.【答案】解:①∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|a﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴a=2,
∴△ABC的周长为:2+2+3=7,
∴△ABC是等腰三角形.
②∵a=5,b=2,c为整数,
∴5﹣2<c<2+5,
∴c的最小值为4,c的最大值为6,
∴△ABC的周长的最大值=5+2+6=13,最小值=5+2+4=11.
【解析】(1)利用绝对值的性质(任何有理数的绝对值都是大于或等于0的数,这是绝对值的非负性)以及偶次方的性质(非负性)得出b和c的值,进而利用三角形三边关系(两边之和大于第三边,两边之差小于第三边)及方程解的定义确定a的值,最后求出该三角形的周长,并判断△ABC的形状;
(2)利用三角形三边关系(两边之和大于第三边,两边之差小于第三边)列不等式,得出c的取值范围,确定c的最大值和最小值,进而求出△ABC的周长的最大值和最小值 .
20.【答案】(1)解:∵AD∥BC,
∴∠A=∠CBE,
∵∠C=∠A,
∴∠C=∠CBE,
∴CD∥AB,
∴∠E=∠CDE
(2)解:∵∠1=75°,
∴∠BFE=∠1=75°,
∵∠E=30°,
∴∠CBE=180°﹣∠BFE﹣∠E=75°,
∵AD∥BC,
∴∠A=∠CBE=75°
【解析】(1)根据平行线的性质可得∠A=∠CBE, 由已知条件可知∠C=∠A,则∠C=∠CBE,推出 CD∥AB, 然后根据平行线的性质进行解答;
(2)根据对顶角的性质可得∠BFE=∠1=75°, 由内角和定理可得∠CBE=180°-∠BFE-∠E=75°,根据平行线的性质可得 ∠A=∠CBE,据此解答.
21.【答案】(1)45
(2)解:由(1)得,即,
又∵∠EDF=30°,
∴,
∵∠DFE=90°,
∴
(3)15°或75°
【解析】【解答】解:(1)∵在△ABC中,∠ACB=90°,∠BAC=45°,
∴,
∵,
∴,
故答案为:;
(3)解:当时,如图所示,
∵∠EDF=30°,即,
∴,
由(1)得,
∴;
当时,如图所示,
∵∠EDF=30°,即,
∴,
∴,
由(1)得,
∴;
综上,∠FAN的度数为或.
(1)根据内角和定理可得∠ABC=45°,由平行线的性质可得∠BAN=∠ABC,据此解答;
(2)由(1)得∠BAN=45°,即∠BAF=45°,由内角和定理可得∠AFD的度数,然后根据∠AFE=∠AFD-∠DFE进行计算;
(3)当∠FAD=∠FDA=30°时,根据∠FAN=∠BAN-∠FAD进行求解;当∠AFD=∠FDA=30°时,由内角和定理可求出∠FAD的度数,然后根据∠FAN=∠FAD-∠BAN进行计算.
22.【答案】(1) 证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC在△ADC和△CEB中 ,
∴△ADC≌△CEB(AAS)
(2) 解:由题意得:AD=2×3=6cm,BE=7×2=14cm,
∵△ADC≌△CEB,
∴EC=AD=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
【解析】 (1) 同角或等角的余角相等可推到出 ∠DAC = ∠BCE ,再利用全等三角形的判定定理AAS证明出 △ADC≌△CEB ;
(2)由(1)的△ADC≌△CEB 可知 EC=AD , DC=BE ,根据题意可以得出AD=6,BE=14,继而求出DE=DC+CE=BE+AD=14+6=20.
23.【答案】(1)解:因为70°,
∵、分别是和的角平分线,
∴
∴
(2)解:在△中,+,
,,
,
,
故
(3)解:.
【解析】【解答】解:(3)理由如下: 因为BM、CN分别是△的两个外角的角平分线,
所以,,
所以+=--()
=---
=
=.
由(2)得,
所以,
所以+=,
所以2(+)=,
所以.
(1)由内角和定理可得∠A1BC+∠A1CB=110°,根据角平分线的概念可得∠A2BC=∠A1BC,∠A2CB=∠A1C B,则∠A2BC+∠A2CB=(∠A1BC+∠A1C B)=55°,再次利用内角和定理就可求出∠2的度数;
(2)由题意可得∠AnBC=∠A1BC,∠AnCB=∠A1C B,则∠AnBC+∠AnCB=(∠A1BC+∠A1C B)=(180°-α),然后根据内角和定理进行解答;
(3)由角平分线的概念以及邻补角的性质可得∠MBE=∠A1BE=(180°-∠A1BC),∠NCF=∠A1CF=(180°-∠A1 CB),则∠MBAn+∠NCAn=360°-∠MBE-∠NCF-(∠AnBC+∠AnCB)=(180°-∠A1)+∠An,然后结合(2)的结论进行解答.
一、单选题
1.现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )
A.10cm B.30cm C.50cm D.70cm
2.某同学把三角形的玻璃打碎成了3块,现要到玻璃店配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去
C.带③去 D.①②③都带去
3.有下列两种图示均表示三角形分类,则正确的是( )
A.①对,②不对 B.②对,①不对
C.①、②都不对 D.①、②都对
4.画的边上的高,正确的是( )
A. B.
C. D.
5.如图,下列各组条件中,不能得到的是( )
A., B.,
C., D.,
6.如图,的两条角平分线,交于点P,若,则为( )
A.112° B.115° C.120° D.125°
7.如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )
A.当∠P=60°时,α=30° B.当∠P=60°时,β=40°
C.当=20°时,∠P=90° D.当β=0°时,∠P=90°
8.如图,点B、E、C、F四点共线,∠B =∠DEF,BE = CF,添加一个条件,不能判定 △ABC ≌ △DEF的是( )
A.∠A=∠D B.AB=DE C.AC∥DF D.AC=DF
9.如图,为了估计一池塘岸边两点A,B之间的距离,小丽同学在池塘一侧选取了一点P,测得PA=5m,PB=4m,那么点A与点B之间的距离不可能是( )
A.6.5m B.7.5m C.8.5m D.9.5m
10.已知下列条件,不能作出唯一三角形的是( )
A.两边及其夹角 B.两角及其夹边
C.三边 D.两边及除夹角外的另一个角
二、填空题
11.在中,若,,则是 三角形.(填“锐角”、“直角”、或“钝角”)
12.如图,有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接并延长到D,使,连接并延长到E,使,连接.经测量,,的长度分别为,,,则A,B之间的距离为 m;
13.若a,b,c是三角形的三边长,化简: .
14.如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是 .
三、作图题
15.如图,在7×7正方形网格中的每个小正方形边长都为1个单位长度,我们把每个小正方形的顶点称为格点,点A、B都为格点,请分别仅用一把无刻度的直尺在所给的网格中画图,保留画图过程的痕迹.
(1)在如图1中找一格点C,画一条线段AB的平行线段CD;
(2)在图2中找一格点E,画出三角形ABE,使得S△ABE=4.
四、解答题
16.已知:如图,在中,,,点D,E分别在和上,且.求证:,并写出最后一步推理的依据.
17.如图,在四边形中,,,平分,平分,则与有何位置关系?试说明理由.
18.如图,在中,,,AD是的角平分线,求的度数.
19.已知a、b、c为△ABC的三边长;
①b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求出该三角形的周长,并判断△ABC的形状.
②若a=5,b=2,且c为整数,求△ABC的周长的最大值和最小值.
五、综合题
20.如图,已知AD∥BC,点E在AB的延长线上,连结DE交BC于点F,且∠C=∠A.
(1)请说明∠E=∠CDE的理由;
(2)若∠1=75°,∠E=30°,求∠A的度数.
21.如图,已知,点A在MN上,点B、C在GH上.在△ABC中,∠ACB=90°,∠BAC=45°.点D、E在直线AB上,在△DEF中,∠DFE=90°,∠EDF=30°.
(1)图中∠BAN的度数是 °;
(2)将△DEF沿直线AB平移,如图2所示,当点F在MN上时,求∠AFE的度数;
(3)将△DEF沿直线AB平移,当以A、D、F为顶点的三角形中,有两个角相等时,请直接写出∠FAN的度数.
22.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合。
(1) 求证:△ADC≌△CEB;
(2) 求两堵木墙之间的距离。
23.已知BM、CN分别是△的两个外角的角平分线,、分别是 和的角平分线,如图①;、分别是和的三等分线(即,),如图②;依此画图,、分别是和的n等分线(即,),且为整数.
(1)若70°,求的度数;
(2)设,请用和n的代数式表示的大小,并写出表示的过程;
(3)当时,请直接写出+与的数量关系.
答案解析
1.【答案】B
【解析】【解答】解:根据三角形的三边关系,得
第三根木棒的长度应大于30-20=10(cm),而小于30+20=50(cm).
故答案为:B.
根据三角形三边关系定理可得“两边之差<第三边<两边之和”可得第三边的范围:10<第三边<50,然后根据各选项即可判断求解.
2.【答案】C
【解析】【解答】解:第①块只保留了原三角形的一个角和部分边,根据这块不能配一块与原来完全一样的;
第②块只保留了原三角形的部分边,根据这两块中的任意一块均不能配一块与原来完全一样的;
第③块不仅保留了原三角形的两个角还保留了一边,则可根据来配一块与原来一样的玻璃.
故答案为:C.
由于③保留两角一边,根据ASA可得全等三角形.
3.【答案】B
【解析】【解答】等腰三角形包括等边三角形,故①的分类不符合题意;图②中的三角形的分类符合题意.
故答案为:B.
根据三角形的分类求解即可。
4.【答案】A
【解析】【解答】解:画△ABC的BC边上的高,即过点A作BC边的垂线.
∴只有选项A符合题意,
故答案为:A.
根据高的定义逐项判断即可。
5.【答案】D
【解析】【解答】解:A、由,,AB=AB,满足SAS能证明,故A不符合题意;
B、,,AB=AB,满足SSS能证明,故B不符合题意;
C、,,AB=AB,满足SAS能证明,故C不符合题意;
D、,,AB=AB,满足SSA,不能证明,故D符合题意;
故答案为:D.
利用全等三角形的判定方法逐项判断即可。
6.【答案】B
【解析】【解答】解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
又∵BD、CE是△ABC的角平分线,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=×130°=65°,
∴∠BPC=180°-65°=115°.
故答案为:B.
根据角平分线的定义可得∠PBC+∠PCB=(∠ABC+∠ACB)=×130°=65°,再利用三角形的内角和求出∠BPC=180°-65°=115°即可。
7.【答案】B
【解析】【解答】解:∵∠ACP=2∠PCD=40°,
∴∠PCD=20°,
∴∠ACD=∠ACP+∠PCD=60°.
∵AB∥CD,
∴∠CAB=180°-∠ACD=120°.
∵∠BAP=α,∠CAP=α+β,
∴∠CAB=2α+β,
∴2α+β=120°,
∴α+β=120°-α,β=120°-2α.
∵∠P+∠CAP+∠ACP=180°,
∴∠P=180°-(α+β+40°)=140°-(α+β)=140°-(120°-α)=20°+α.
当∠P=60°时,20°+α=60°,此时α=40°,故A错误,B正确;
当β=20°时,120°-2α=20°,此时α=50°,
∴∠P=20°+α=70°,故C错误;
当β=0°时,120°-2α=0°,此时α=60°,
∴∠P=20°+α=80°,故D错误.
故答案为:B.
由已知条件可得∠PCD=20°,则∠ACD=∠ACP+∠PCD=60°,根据平行线的性质可得∠CAB=180°-∠ACD=120°,由角的和差关系可得∠CAB=2α+β,则2α+β=120°,进而可得α+β=120°-α,β=120°-2α,由内角和定理可得∠P=20°+α,据此判断.
8.【答案】D
【解析】【解答】解:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
A.∠A=∠D,∠B=∠DEF,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;
B.AB=DE,∠B=∠DEF,BC=EF,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;
C.∵AC∥DF,∴∠ACB=∠F,
∠B=∠DEF,BC=EF,∠ACB=∠F,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;
D.AC=DF,BC=EF,∠B=∠DEF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
故答案为:D.
根据题意先求出BC=EF,再利用全等三角形的判定方法对每个选项一一判断即可。
9.【答案】D
【解析】【解答】解:∵PA、PB、AB能构成三角形,
∴PA﹣PB<AB<PA+PB,即1m<AB<9m,故D正确.
故答案为:D.
三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出AB的范围,进而判断.
10.【答案】D
【解析】【解答】解:A、B、C分别符合全等三角形的判定SAS、ASA、SSS,故能作出唯一三角形;
D、已知两边及除夹角外的另一个角,不能作出唯一三角形,如等腰三角形底边上的任一点与顶点之间的线段两侧的三角形,错误;
故选D.
看是否符合所学的全等的公理或定理即可.
11.【答案】直角
【解析】【解答】解:∵,
∴,
设,则,根据题意得:
,
解得:,
则,
∴是直角三角形.
故答案为:直角.
先利用三角形的内角和及求出三角形的三个内角,再判断即可。
12.【答案】800
【解析】【解答】解:在△ABC和△EDC中,
∴△ABC≌△EDC(SAS),
∴AB=DE=800.
故答案为:800.
利用“SAS”证明△ABC≌△EDC,再利用全等三角形的性质可得AB=DE=800。
13.【答案】2c-2b
【解析】【解答】解:∵a,b,c是三角形的三边长,
∴,
∴
,
故答案为:2c-2b.
根据三角形三边关系定理“三角形任意两边之和大于第三边”可得a+c>b,a+b>c,于是可得a+c-b>0,c-a-b<0,然后根据绝对值的非负性可去绝对值求解.
14.【答案】2
【解析】【解答】解:∵FC∥AB,
∴∠A=∠ECF,
又∵∠AEC=∠CEF,
在△AED和△CEF中,
,
∴△AED≌△CEF(ASA),
∴AD=CF=5,
∴BD=AD-AB=5-3=2.
故答案为:2.
根据平行线的性质得出∠A=∠ECF,根据对顶角相等得出∠AEC=∠CEF,再利用ASA证明△AED≌△CEF,得出AD=CF=5,最后根据线段和差求BD长即可.
15.【答案】(1)解:如图,线段CD即为所求;
(2)解:如图,△ABE即为所求.
【解析】(1)根据题意作图即可;
(2)根据题意作三角形即可。
16.【答案】证明:∵在中,,,
∴,
∵,
∴,
∴(同位角相等,两直线平行).
【解析】利用三角形内角和定理求出∠B=50°,即得∠B=∠ADE,根据同位角相等,两直线平行即证结论.
17.【答案】结论:BE和DF的位置关系时平行
证明:∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABC=2∠2,∠ADC=2∠4,
∴2∠2+2∠4=180°,
∴∠2+∠4=90°,
∵∠4+∠DFC=90°,
∴∠2=∠DFC,
∴BE∥DF
【解析】利用已知可知∠ABC+∠ADC=180°,利用角平分线的性质可推出∠ABC=2∠2,∠ADC=2∠4,由此可证得∠2+∠4=90°,利用三角形的内角和定理可证得∠4+∠DFC=90°,利用余角的性质可得到∠2=∠DFC,利用同位角相等,两直线平行,可证得结论.
18.【答案】解:在中,(三角形内角和定理).
∵,(已知),
∴(等式的性质).
∵AD平分(已知),
∴(角平分线的定义).
在中,(三角形内角和定理).
∵(已知),(已证),
∴(等式的性质).
【解析】根据三角形的内角和定理算出∠BAC的度数,由角平分线定义算出∠BAD的度数,再由三角形内角和定理算出∠ADB的度数.
19.【答案】解:①∵(b﹣2)2+|c﹣3|=0,
∴b﹣2=0,c﹣3=0,
解得:b=2,c=3,
∵a为方程|a﹣4|=2的解,
∴a﹣4=±2,
解得:a=6或2,
∵a、b、c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴a=2,
∴△ABC的周长为:2+2+3=7,
∴△ABC是等腰三角形.
②∵a=5,b=2,c为整数,
∴5﹣2<c<2+5,
∴c的最小值为4,c的最大值为6,
∴△ABC的周长的最大值=5+2+6=13,最小值=5+2+4=11.
【解析】(1)利用绝对值的性质(任何有理数的绝对值都是大于或等于0的数,这是绝对值的非负性)以及偶次方的性质(非负性)得出b和c的值,进而利用三角形三边关系(两边之和大于第三边,两边之差小于第三边)及方程解的定义确定a的值,最后求出该三角形的周长,并判断△ABC的形状;
(2)利用三角形三边关系(两边之和大于第三边,两边之差小于第三边)列不等式,得出c的取值范围,确定c的最大值和最小值,进而求出△ABC的周长的最大值和最小值 .
20.【答案】(1)解:∵AD∥BC,
∴∠A=∠CBE,
∵∠C=∠A,
∴∠C=∠CBE,
∴CD∥AB,
∴∠E=∠CDE
(2)解:∵∠1=75°,
∴∠BFE=∠1=75°,
∵∠E=30°,
∴∠CBE=180°﹣∠BFE﹣∠E=75°,
∵AD∥BC,
∴∠A=∠CBE=75°
【解析】(1)根据平行线的性质可得∠A=∠CBE, 由已知条件可知∠C=∠A,则∠C=∠CBE,推出 CD∥AB, 然后根据平行线的性质进行解答;
(2)根据对顶角的性质可得∠BFE=∠1=75°, 由内角和定理可得∠CBE=180°-∠BFE-∠E=75°,根据平行线的性质可得 ∠A=∠CBE,据此解答.
21.【答案】(1)45
(2)解:由(1)得,即,
又∵∠EDF=30°,
∴,
∵∠DFE=90°,
∴
(3)15°或75°
【解析】【解答】解:(1)∵在△ABC中,∠ACB=90°,∠BAC=45°,
∴,
∵,
∴,
故答案为:;
(3)解:当时,如图所示,
∵∠EDF=30°,即,
∴,
由(1)得,
∴;
当时,如图所示,
∵∠EDF=30°,即,
∴,
∴,
由(1)得,
∴;
综上,∠FAN的度数为或.
(1)根据内角和定理可得∠ABC=45°,由平行线的性质可得∠BAN=∠ABC,据此解答;
(2)由(1)得∠BAN=45°,即∠BAF=45°,由内角和定理可得∠AFD的度数,然后根据∠AFE=∠AFD-∠DFE进行计算;
(3)当∠FAD=∠FDA=30°时,根据∠FAN=∠BAN-∠FAD进行求解;当∠AFD=∠FDA=30°时,由内角和定理可求出∠FAD的度数,然后根据∠FAN=∠FAD-∠BAN进行计算.
22.【答案】(1) 证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC在△ADC和△CEB中 ,
∴△ADC≌△CEB(AAS)
(2) 解:由题意得:AD=2×3=6cm,BE=7×2=14cm,
∵△ADC≌△CEB,
∴EC=AD=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
【解析】 (1) 同角或等角的余角相等可推到出 ∠DAC = ∠BCE ,再利用全等三角形的判定定理AAS证明出 △ADC≌△CEB ;
(2)由(1)的△ADC≌△CEB 可知 EC=AD , DC=BE ,根据题意可以得出AD=6,BE=14,继而求出DE=DC+CE=BE+AD=14+6=20.
23.【答案】(1)解:因为70°,
∵、分别是和的角平分线,
∴
∴
(2)解:在△中,+,
,,
,
,
故
(3)解:.
【解析】【解答】解:(3)理由如下: 因为BM、CN分别是△的两个外角的角平分线,
所以,,
所以+=--()
=---
=
=.
由(2)得,
所以,
所以+=,
所以2(+)=,
所以.
(1)由内角和定理可得∠A1BC+∠A1CB=110°,根据角平分线的概念可得∠A2BC=∠A1BC,∠A2CB=∠A1C B,则∠A2BC+∠A2CB=(∠A1BC+∠A1C B)=55°,再次利用内角和定理就可求出∠2的度数;
(2)由题意可得∠AnBC=∠A1BC,∠AnCB=∠A1C B,则∠AnBC+∠AnCB=(∠A1BC+∠A1C B)=(180°-α),然后根据内角和定理进行解答;
(3)由角平分线的概念以及邻补角的性质可得∠MBE=∠A1BE=(180°-∠A1BC),∠NCF=∠A1CF=(180°-∠A1 CB),则∠MBAn+∠NCAn=360°-∠MBE-∠NCF-(∠AnBC+∠AnCB)=(180°-∠A1)+∠An,然后结合(2)的结论进行解答.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
