人教版数学八年级下册19.2.3一次函数与方程、不等式 说课课件 (共33张PPT)
文档属性
| 名称 | 人教版数学八年级下册19.2.3一次函数与方程、不等式 说课课件 (共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 830.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 12:57:20 | ||
图片预览







文档简介
(共33张PPT)
19.2.3一次函数与方程、不等式h
教学过程
教法学法
学情分析
教材分析
板书设计
教后反思
教材地位与作用重点难点132教学目标一、教材分析h 本节课是八年级下册第十九章第2节的第六课时,主要学习内容是一次函数和方程、不等式以及方程组的关系,它是用函数解决实际问题的工具,而且是数形结合的一个典范,对提升学生的思维品质有重要帮助.
1、教材地位与作用
hh
二、学情分析
八年级下期,学生已经有一定的数学感知能力, 而函数、方程和不等式是初中数学的核心内容,但他们没有建立这些知识的有效联系,因此要引导学生以函数图象为中介,用函数的观点看方程和不等式.
学法教法
学生
教师
开放
激趣
引导
自主
合作
探究
三、教法学法
(一)
创设情境,导入新课
(二)
合作交流,探索新知
(三)
练习巩固,逐步提高
(四)
引导总结,交流收获
四、教学过程
(一)创设情境 导入新课
雾霾天气对人类的健康造成了威胁,人们想了解PM2.5和海拔高度之间的关系,于是让1号探测气球从海拔-1m 处出发,以2 m/min 的速度上升进行测试.
(1)用式子分别表示 1号气球所在位置的海拔 y(m)与气球上升时间 x(min)的函数关系.
(2)什么时候,1号气球能到达海平面?
什么时候,在海平面以上?
什么时候,在海平面以下?
设计意图
简单明了的情景导入,贴近生活,能在短时间内使学生集中注意力,激发求知欲.
1、一次函数与一元一次方程
合作交流
探索新知
2、一次函数与一元一次不等式
3、一次函数与二元一次方程组
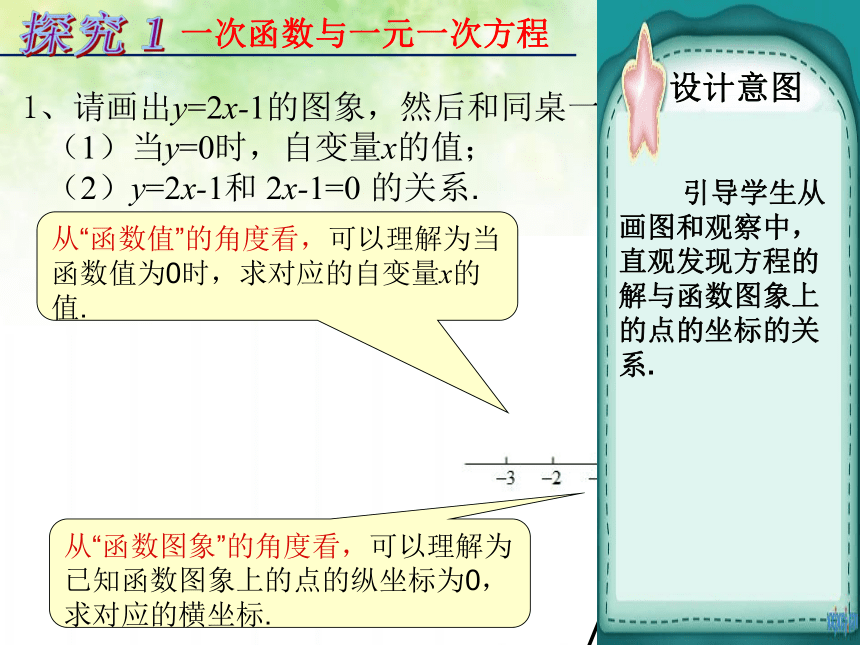
1、请画出y=2x-1的图象,然后和同桌一起讨论
(1)当y=0时,自变量x的值;
(2)y=2x-1和 2x-1=0 的关系.
y=2x-1
从“函数图象”的角度看,可以理解为已知函数图象上的点的纵坐标为0,求对应的横坐标.
一次函数与一元一次方程
探究1
从“函数值”的角度看,可以理解为当函数值为0时,求对应的自变量x的值.
设计意图
引导学生从画图和观察中,直观发现方程的解与函数图象上的点的坐标的关系.
y=-x+2
2、(1)请画出y=-x+2的图象,它与x轴的交点坐
标是什么?
(2)方程-x+2=0解是_ _;
(3)它们之间有什么联系?
x=2
方程ax+b=0的解就是函数y=ax+b的图象与x轴交点的横坐标.
一次函数与一元一次方程
探究1
ax+b=0的解
一次函数y=ax+b中,y=0时,x的值.
一次函数y=ax+b 的图象与x轴交点的横坐标 .
从形看
从数看
ax+b=0的解
归纳
数
形
结
合
一次函数y=ax+b与一元一次方程ax+b=0(a≠0)的关系
一次函数与一元一次方程
探究1
由特殊到一般
y=2x-1
快乐升级
一次函数与一元一次方程
探究1
x 时, y=3
=2
观察图象
x_ _时, y=-3
=-1
用函数的观点看:
解一元一次方程 ax +b =m 就是求当函数值为m时,对应的自变量的值.
m=0时,点在x轴上;
m>0时,点在x轴的上方;
m<0时,点在x轴的下方.
ax+b=0的解
一次函数y=ax+b中,y=0时,x的值.
一次函数y=ax+b 的图象上y= 0 时点的横坐标 .
从形看
从数看
ax+b=0的解
归纳
一次函数y=ax+b 与一元一次方程ax+b=0(a≠0)的关系
m
m
m
m
m
深入思考,揭示本质
一次函数与一元一次方程
探究1
设计意图
学生在经历了自主探索、合作交流后,总结了一次函数和一元一次方程的关系,在这个过程中体会到了数学学习的成功.
课堂练习1
1、函数y=ax+b的图象如图所示,
x
y
0
-3
2
x 时, y=0
x 时, y=2
2、(1)已知方程ax+b=0的解是x=1,则直线y=ax+b与x轴
的交点坐标为 .
(2)已知方程ax+b=5的解是x=3,可知点( , )
一定在函数y=ax+b的图象上.
一次函数与一元一次方程
探究1
课堂练习1
3、思考:
(1)方程x+5=2的解与函数y=x+3的图象和x轴
交点的横坐标为有什么关系?
(2)ax+n=m(a≠0)可看做哪条直线与x轴交点
的横坐标?
ax+n=m(a≠0)可通过合并同类项转化成y=kx+b(k≠0)的形式,也就是求相应的函数图象与x轴交点的横坐标.
再次升级
一次函数与一元一次方程
探究1
设计意图
思考的再度深入,使本质得以揭示。多次归纳是为了给本节课的重点,即一次函数与二元一次方程组关系的探究奠定基础.
一次函数与一元一次不等式
探究2
x 时, y>0
x 时, y<0
x 时, y=0
=0.5
>0.5
<0.5
观察图象
y=2x-1
一次函数与一元一次不等式
探究2
观察图象
x 时, y>1
x 时, y<1
>1
<1
用函数的观点看:
解一元一次不等式 ax +b >m 或ax +b由特殊到一般
快乐升级
y=2x-1
ax+b>0或ax+b<0的解集
一次函数y=ax+b中,y>0或y<0时,自变量x的取值范围.
直线y= ax+b上纵坐标大于0或小于0时,横坐标满足的条件.
从形看
从数看
ax+b>0或ax+b<0的解集
数形结合
归纳
一次函数y=ax+b 与一元一次不等式ax+b>0或ax+b<0 的关系(a≠0)
一次函数与一元一次不等式
探究2
m
m
m
m
m
m
m
m
m
m
设计意图
类比一次函数和方程的关系,学生可熟练总结出一次函数与一元一次不等式的关系,达到学以致用的目的.
一次函数y=ax+b的图象如图所示,请回答下列问题.
(1) x 时, y>0;
(2) x 时, y<4;
(3) x 时, y>6;
(4) x 时, y<-4.
课堂练习2
一次函数与一元一次不等式
探究2
设计意图
题型简单,但4个点的设计能很好地考察学生对一次函数和一元一次不等式关系的掌握情况.
为了更准确了解PM2.5和海拔高度之间的关系,又增加了2号探测气球,从海拔1m 处出发,以1 m/min 的速度上升进行测试.
(1)用式子分别表示 2号气球所在位置的海拔 y(m)与气球 上升时间 x(min)的函数关系.
(2)什么时候,1号气球和2号气球到达相同的海拔高度 ?
分析:
(1)y=x+1(x≥0)
(2) 1号气球和2号气球到达相同的海
拔高度 ,即当函数值一样时,
求两个函数的自变量值,以及函
数值.
一次函数与二元一次方程组
探究3
(1)由图象可看出直线 y=2x-1和 y=x+1的交点坐标为 .
请在同一直角坐标系中画y=2x-1和y=x+1的图象.
y =2x-1
y =x+1
(2)方程组 的解
是 .
一次函数与二元一次方程组
探究3
(2,3)
(3)函数y=2x-1、y=x+1和方程
组 有什么关系?
设计意图
引导学生用函数的观点,从数和形两方面深化对二元一次方程组解得认识,为形成一次函数与二元一次方程组关系的归纳提供样例.
自变量为何值时,两个函数的函数值相等,以及这个函数值是多少.
确定两条直线交点的坐标.
从形看
从数看
数形结合
一次函数与二元一次方程组的关系
归纳
二元一次方程组的解
二元一次方程组的解
一次函数与二元一次方程组
探究3
1、一次函数y=ax+c和y=kx+b的图象分别如图1、图2
所示,请写出方程组 的解分别
为(1) ; (2) .
课堂练习3
x
y
O
y=kx +b
4
y=ax +c
-2
x
y
O
y=kx +b
1
y=ax +c
2
一次函数与二元一次方程组
探究3
图1
图2
课堂检测
(三)练习巩固,逐步提高
1、函数y=kx+b(k<0)与x轴交于点(3,0),
关于x的不等式kx+b>0的解集是( )
A. x<3 B. x>3
C. x>0 D. x<0
2、函数y=x+5,当x为何值时,对应的函数值y
(1)等于3? (2)大于3? (3)小于3?
3、画图象解方程组
x
y
O
y=kx +b
3
设计意图
在习题的设置上,由浅入深,层层递进,突出由知识到能力的递进发展特性,全面考察了学生对本节课内容的掌握情况.
说一说你的收获和体会
(四)引导总结,交流收获
(1)请用函数的观点,从数形两方面说说你对一元
一次方程、一元一次不等式和二元一次方程组
有什么新的理解.
(2)这些知识你是如何得到的?
(3)你认为这些知识对以后的学习有什么帮助?
收获和体会
(四)引导总结,交流收获
分层作业
1、必做题:课本99页,第8题
2、选做题:
在同一直角坐标系中,画出函数3x+y=4和2x-y=1的图象,并结合图象回答,当x在什么范围时, 3x+y=4的函数值大于2x-y=1的函数值。
设计意图
分层作业是为了让每个孩子都能在本节课学有所获,体会到成功的喜悦.选做题是探讨一次函数和一元一次不等式组的关系,是对本节课内容的再次提升.
19.2.3 一次函数与方程、不等式
一次函数和方程的关系 练习
一次函数与不等式的关系
一次函数与方程组的关系
五、 板书设计
本节课通过情景引课,激发学生学习的兴趣,在探究中设置问题,引发学生对函数和方程、不等式关系的思考;在教学中注重培养学生用函数的观点看方程、不等式和方程组的习惯;同时也要熟练掌握读图的正确方法。这节课加强了知识间联系,对已有知识进行了整合。使学生看问题的角度和高度发生了变化,认识也更加深刻.
六、 教后反思
谢 谢 !
19.2.3一次函数与方程、不等式h
教学过程
教法学法
学情分析
教材分析
板书设计
教后反思
教材地位与作用重点难点132教学目标一、教材分析h 本节课是八年级下册第十九章第2节的第六课时,主要学习内容是一次函数和方程、不等式以及方程组的关系,它是用函数解决实际问题的工具,而且是数形结合的一个典范,对提升学生的思维品质有重要帮助.
1、教材地位与作用
hh
二、学情分析
八年级下期,学生已经有一定的数学感知能力, 而函数、方程和不等式是初中数学的核心内容,但他们没有建立这些知识的有效联系,因此要引导学生以函数图象为中介,用函数的观点看方程和不等式.
学法教法
学生
教师
开放
激趣
引导
自主
合作
探究
三、教法学法
(一)
创设情境,导入新课
(二)
合作交流,探索新知
(三)
练习巩固,逐步提高
(四)
引导总结,交流收获
四、教学过程
(一)创设情境 导入新课
雾霾天气对人类的健康造成了威胁,人们想了解PM2.5和海拔高度之间的关系,于是让1号探测气球从海拔-1m 处出发,以2 m/min 的速度上升进行测试.
(1)用式子分别表示 1号气球所在位置的海拔 y(m)与气球上升时间 x(min)的函数关系.
(2)什么时候,1号气球能到达海平面?
什么时候,在海平面以上?
什么时候,在海平面以下?
设计意图
简单明了的情景导入,贴近生活,能在短时间内使学生集中注意力,激发求知欲.
1、一次函数与一元一次方程
合作交流
探索新知
2、一次函数与一元一次不等式
3、一次函数与二元一次方程组
1、请画出y=2x-1的图象,然后和同桌一起讨论
(1)当y=0时,自变量x的值;
(2)y=2x-1和 2x-1=0 的关系.
y=2x-1
从“函数图象”的角度看,可以理解为已知函数图象上的点的纵坐标为0,求对应的横坐标.
一次函数与一元一次方程
探究1
从“函数值”的角度看,可以理解为当函数值为0时,求对应的自变量x的值.
设计意图
引导学生从画图和观察中,直观发现方程的解与函数图象上的点的坐标的关系.
y=-x+2
2、(1)请画出y=-x+2的图象,它与x轴的交点坐
标是什么?
(2)方程-x+2=0解是_ _;
(3)它们之间有什么联系?
x=2
方程ax+b=0的解就是函数y=ax+b的图象与x轴交点的横坐标.
一次函数与一元一次方程
探究1
ax+b=0的解
一次函数y=ax+b中,y=0时,x的值.
一次函数y=ax+b 的图象与x轴交点的横坐标 .
从形看
从数看
ax+b=0的解
归纳
数
形
结
合
一次函数y=ax+b与一元一次方程ax+b=0(a≠0)的关系
一次函数与一元一次方程
探究1
由特殊到一般
y=2x-1
快乐升级
一次函数与一元一次方程
探究1
x 时, y=3
=2
观察图象
x_ _时, y=-3
=-1
用函数的观点看:
解一元一次方程 ax +b =m 就是求当函数值为m时,对应的自变量的值.
m=0时,点在x轴上;
m>0时,点在x轴的上方;
m<0时,点在x轴的下方.
ax+b=0的解
一次函数y=ax+b中,y=0时,x的值.
一次函数y=ax+b 的图象上y= 0 时点的横坐标 .
从形看
从数看
ax+b=0的解
归纳
一次函数y=ax+b 与一元一次方程ax+b=0(a≠0)的关系
m
m
m
m
m
深入思考,揭示本质
一次函数与一元一次方程
探究1
设计意图
学生在经历了自主探索、合作交流后,总结了一次函数和一元一次方程的关系,在这个过程中体会到了数学学习的成功.
课堂练习1
1、函数y=ax+b的图象如图所示,
x
y
0
-3
2
x 时, y=0
x 时, y=2
2、(1)已知方程ax+b=0的解是x=1,则直线y=ax+b与x轴
的交点坐标为 .
(2)已知方程ax+b=5的解是x=3,可知点( , )
一定在函数y=ax+b的图象上.
一次函数与一元一次方程
探究1
课堂练习1
3、思考:
(1)方程x+5=2的解与函数y=x+3的图象和x轴
交点的横坐标为有什么关系?
(2)ax+n=m(a≠0)可看做哪条直线与x轴交点
的横坐标?
ax+n=m(a≠0)可通过合并同类项转化成y=kx+b(k≠0)的形式,也就是求相应的函数图象与x轴交点的横坐标.
再次升级
一次函数与一元一次方程
探究1
设计意图
思考的再度深入,使本质得以揭示。多次归纳是为了给本节课的重点,即一次函数与二元一次方程组关系的探究奠定基础.
一次函数与一元一次不等式
探究2
x 时, y>0
x 时, y<0
x 时, y=0
=0.5
>0.5
<0.5
观察图象
y=2x-1
一次函数与一元一次不等式
探究2
观察图象
x 时, y>1
x 时, y<1
>1
<1
用函数的观点看:
解一元一次不等式 ax +b >m 或ax +b
快乐升级
y=2x-1
ax+b>0或ax+b<0的解集
一次函数y=ax+b中,y>0或y<0时,自变量x的取值范围.
直线y= ax+b上纵坐标大于0或小于0时,横坐标满足的条件.
从形看
从数看
ax+b>0或ax+b<0的解集
数形结合
归纳
一次函数y=ax+b 与一元一次不等式ax+b>0或ax+b<0 的关系(a≠0)
一次函数与一元一次不等式
探究2
m
m
m
m
m
m
m
m
m
m
设计意图
类比一次函数和方程的关系,学生可熟练总结出一次函数与一元一次不等式的关系,达到学以致用的目的.
一次函数y=ax+b的图象如图所示,请回答下列问题.
(1) x 时, y>0;
(2) x 时, y<4;
(3) x 时, y>6;
(4) x 时, y<-4.
课堂练习2
一次函数与一元一次不等式
探究2
设计意图
题型简单,但4个点的设计能很好地考察学生对一次函数和一元一次不等式关系的掌握情况.
为了更准确了解PM2.5和海拔高度之间的关系,又增加了2号探测气球,从海拔1m 处出发,以1 m/min 的速度上升进行测试.
(1)用式子分别表示 2号气球所在位置的海拔 y(m)与气球 上升时间 x(min)的函数关系.
(2)什么时候,1号气球和2号气球到达相同的海拔高度 ?
分析:
(1)y=x+1(x≥0)
(2) 1号气球和2号气球到达相同的海
拔高度 ,即当函数值一样时,
求两个函数的自变量值,以及函
数值.
一次函数与二元一次方程组
探究3
(1)由图象可看出直线 y=2x-1和 y=x+1的交点坐标为 .
请在同一直角坐标系中画y=2x-1和y=x+1的图象.
y =2x-1
y =x+1
(2)方程组 的解
是 .
一次函数与二元一次方程组
探究3
(2,3)
(3)函数y=2x-1、y=x+1和方程
组 有什么关系?
设计意图
引导学生用函数的观点,从数和形两方面深化对二元一次方程组解得认识,为形成一次函数与二元一次方程组关系的归纳提供样例.
自变量为何值时,两个函数的函数值相等,以及这个函数值是多少.
确定两条直线交点的坐标.
从形看
从数看
数形结合
一次函数与二元一次方程组的关系
归纳
二元一次方程组的解
二元一次方程组的解
一次函数与二元一次方程组
探究3
1、一次函数y=ax+c和y=kx+b的图象分别如图1、图2
所示,请写出方程组 的解分别
为(1) ; (2) .
课堂练习3
x
y
O
y=kx +b
4
y=ax +c
-2
x
y
O
y=kx +b
1
y=ax +c
2
一次函数与二元一次方程组
探究3
图1
图2
课堂检测
(三)练习巩固,逐步提高
1、函数y=kx+b(k<0)与x轴交于点(3,0),
关于x的不等式kx+b>0的解集是( )
A. x<3 B. x>3
C. x>0 D. x<0
2、函数y=x+5,当x为何值时,对应的函数值y
(1)等于3? (2)大于3? (3)小于3?
3、画图象解方程组
x
y
O
y=kx +b
3
设计意图
在习题的设置上,由浅入深,层层递进,突出由知识到能力的递进发展特性,全面考察了学生对本节课内容的掌握情况.
说一说你的收获和体会
(四)引导总结,交流收获
(1)请用函数的观点,从数形两方面说说你对一元
一次方程、一元一次不等式和二元一次方程组
有什么新的理解.
(2)这些知识你是如何得到的?
(3)你认为这些知识对以后的学习有什么帮助?
收获和体会
(四)引导总结,交流收获
分层作业
1、必做题:课本99页,第8题
2、选做题:
在同一直角坐标系中,画出函数3x+y=4和2x-y=1的图象,并结合图象回答,当x在什么范围时, 3x+y=4的函数值大于2x-y=1的函数值。
设计意图
分层作业是为了让每个孩子都能在本节课学有所获,体会到成功的喜悦.选做题是探讨一次函数和一元一次不等式组的关系,是对本节课内容的再次提升.
19.2.3 一次函数与方程、不等式
一次函数和方程的关系 练习
一次函数与不等式的关系
一次函数与方程组的关系
五、 板书设计
本节课通过情景引课,激发学生学习的兴趣,在探究中设置问题,引发学生对函数和方程、不等式关系的思考;在教学中注重培养学生用函数的观点看方程、不等式和方程组的习惯;同时也要熟练掌握读图的正确方法。这节课加强了知识间联系,对已有知识进行了整合。使学生看问题的角度和高度发生了变化,认识也更加深刻.
六、 教后反思
谢 谢 !
