鲁教版(五四学制)数学八年级上册第四章图形的平移与旋转 综合素质评价(含解析)
文档属性
| 名称 | 鲁教版(五四学制)数学八年级上册第四章图形的平移与旋转 综合素质评价(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 689.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 13:03:37 | ||
图片预览



文档简介
第四章图形的平移与旋转 综合素质评价
一、选择题(每题3分,共36分)
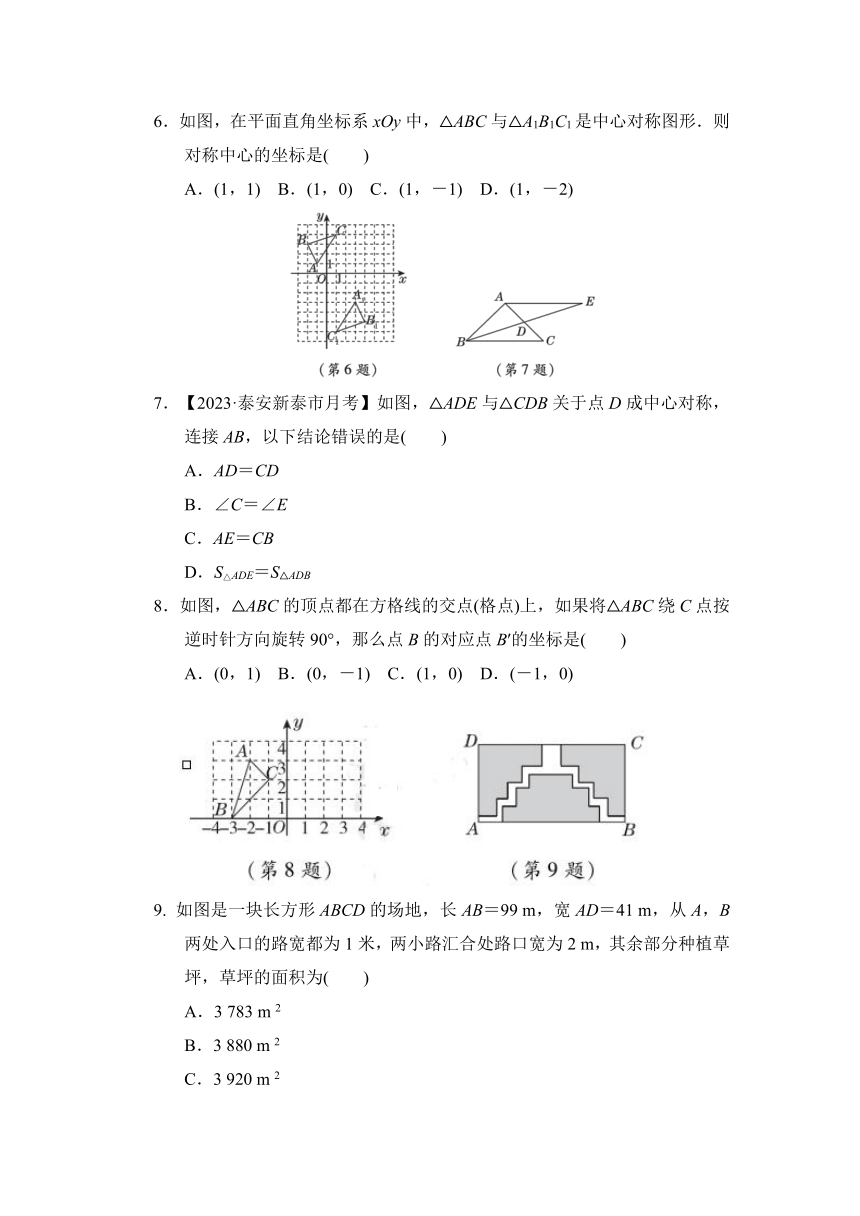
1.在下面四个选项的图形中,不能由如图所示的图形经过旋转或平移得到的是( )
2.【2022·郴州】下列图形既是轴对称图形又是中心对称图形的是( )
3.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,6),B(-3,-3).将线段AB平移后A点的对应点是A′(10,10),则点B的对应点B′的坐标为( )
A.(10,10)
B.(-3,-3)
C.(-3,3)
D.(7,1)
4.【2022·遵义】在平面直角坐标系中,点A(a,1)与点B(-2,b)关于原点成中心对称,则a+b的值为( )
A.-3 B.-1 C.1 D.3
5.如图,将△ABC绕点A逆时针旋转90°得到△ADE,点B,C的对应点分别为D,E,若AB=1,则BD的长为( )
A.1 B. C.2 D.2
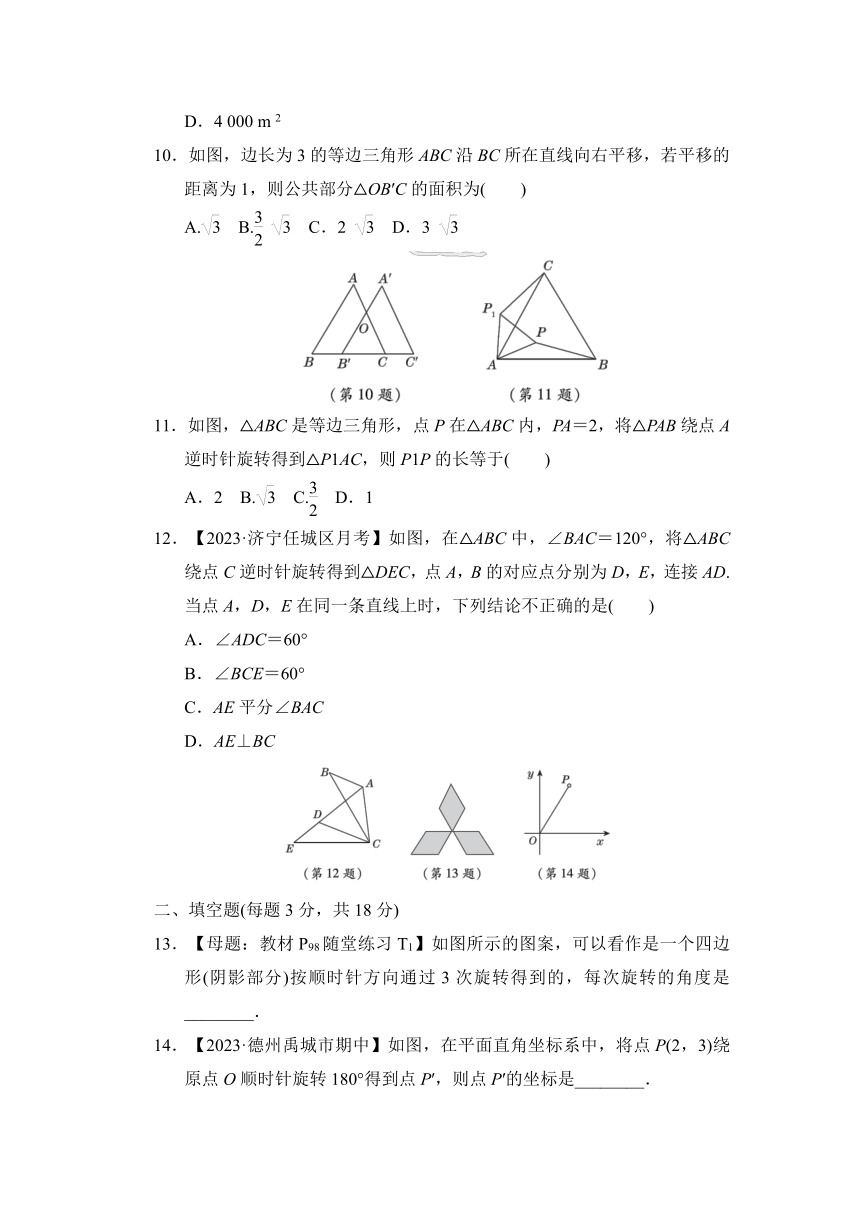
6.如图,在平面直角坐标系xOy中,△ABC与△A1B1C1是中心对称图形.则对称中心的坐标是( )
A.(1,1) B.(1,0) C.(1,-1) D.(1,-2)
7.【2023·泰安新泰市月考】如图,△ADE与△CDB关于点D成中心对称,连接AB,以下结论错误的是( )
A.AD=CD
B.∠C=∠E
C.AE=CB
D.S△ADE=S△ADB
8.如图,△ABC的顶点都在方格线的交点(格点)上,如果将△ABC绕C点按逆时针方向旋转90°,那么点B的对应点B′的坐标是( )
A.(0,1) B.(0,-1) C.(1,0) D.(-1,0)
9. 如图是一块长方形ABCD的场地,长AB=99 m,宽AD=41 m,从A,B两处入口的路宽都为1米,两小路汇合处路口宽为2 m,其余部分种植草坪,草坪的面积为( )
A.3 783 m 2
B.3 880 m 2
C.3 920 m 2
D.4 000 m 2
10.如图,边长为3的等边三角形ABC沿BC所在直线向右平移,若平移的距离为1,则公共部分△OB′C的面积为( )
A. B. C.2 D.3
11.如图,△ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )
A.2 B. C. D.1
12.【2023·济宁任城区月考】如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论不正确的是( )
A.∠ADC=60°
B.∠BCE=60°
C.AE平分∠BAC
D.AE⊥BC
二、填空题(每题3分,共18分)
13.【母题:教材P98随堂练习T1】如图所示的图案,可以看作是一个四边形(阴影部分)按顺时针方向通过3次旋转得到的,每次旋转的角度是________.
14.【2023·德州禹城市期中】如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转180°得到点P′,则点P′的坐标是________.
15.如图,射线AC,BD分别与直线l交于点A,B.现将射线AC沿直线l向右平移过点B,若∠1=46°,∠2=72°,则∠3的度数为________.
16.如图,射线OM,ON互相垂直,OA=8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连接AB,AB=5.将线段AB绕点O逆时针旋转得到线段A′B′,若点B′恰好落在射线ON上,则点A′到射线ON的距离d=________.
17.如图,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),AO=AB,将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′,B′在x轴上.则点B′的坐标是________.
18.一副三角板按如图所示叠放在一起,∠C=60°,∠OAB=45°,其中点B,D重合,若固定三角板AOB,将三角板ACD绕着公共顶点A顺时针旋转一周后停止,当旋转角为________时,CD∥AO.
三、解答题(23题12分,24题14分,其余每题10分,共66分)
19.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别是A(-1,4),B(-3,1).
(1)画出线段AB向右平移4个单位长度后的线段A1B1;
(2)画出线段AB绕原点O旋转180°后的线段A2B2.
20.【母题:教材P112习题T2】如图,在6×6的网格中已经涂色了三个小正方形,请按下列要求画图.
(1)在图①中涂色一个小正方形,使涂色的四个小正方形组成一个轴对称图形.
(2)在图②中涂色一个小正方形,使涂色的四个小正方形组成一个中心对称图形.
21.如图,△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.
22.如图,在△ABC中,AF⊥BC于点F.将△ABC绕点A顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上.
(1)若∠B=50°,求∠DAF的度数;
(2)若∠E=∠CAD,求证:AD=CD.
23.△ABC在平面直角坐标系中如图所示,每个顶点都在格点上.
(1)求△ABC的面积;
(2)若△ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+3,y0+4),请画出△ABC平移后得到的△A1B1C1,并写出点A1,B1,C1的坐标;
(3)在x轴上是否存在点Q,使以A1,B,Q三点为顶点的三角形的面积为3?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
24.已知△ABC是等腰直角三角形,∠ACB=90°,点D是平面内任意一点,CD绕着点C逆时针旋转90°到CE.
(1)如图①,若D为△ABC内一点,求证:AD=BE;
(2)如图②,若D为AB边上一点,AD=5,BD=12,求DE的长.
答案
一、1.A 2.B
3.D 【点拨】由点A(0,6),A′(10,10)可知平移方式是向右平移10个单位长度,向上平移4个单位长度,∴点B(-3,-3)向右平移10个单位长度,向上平移4个单位长度得到B′(-3+10,-3+4),即(7,1).
4.C
5.B 【点拨】∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴AD=AB,∠BAD=90°,
∴△ABD是等腰直角三角形.
由勾股定理,得BD=AB.
∵AB=1,∴BD=.
6.C 【点拨】连接AA1,CC1,两线交点即为对称中心.
7.B 【点拨】∵△ADE与△CDB关于点D成中心对称,
∴AD=CD,BD=ED,AE=CB,∠E=∠CBD,
∵BD=ED,∴S△ABD=S△ADE.
8.C 【点拨】如图,可知B′的坐标为(1,0).
9.B 【点拨】(99-2)×(41-1)=97×40=3 880(平方米),
∴种植草坪面积为3 880平方米.
10.A 【点拨】如图,过点O作OH⊥BC于点H,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
由平移的性质可知BB′=1,∠A′B′C′=∠ABC=60°,
∴B′C=3-1=2,△OB′C为等边三角形,
∴OC=2,∴OH=,
∴S△OB′C=×2×=.
11.A 【点拨】∵△ABC是等边三角形,
∴AC=AB,∠CAB=60°.
∵将△PAB绕点A逆时针旋转得到△P1AC,
∴AP1=AP,∠CAP1=∠BAP,
∴∠CAB=∠CAP+∠BAP=∠CAP+∠CAP1=60°,即∠PAP1=60°,
∴△APP1是等边三角形,
∴P1P=PA=2.
12.D 【点拨】由旋转的性质可知∠EDC=∠BAC=120°,
∴当点A,D,E在同一条直线上时,∠ADC=180°-∠EDC=60°,A正确;
由旋转的性质可知△BAC≌△EDC,
∴∠BCA=∠ECD,CA=CD.
又∵∠ADC=60°,
∴△ACD为等边三角形,∴∠ACD=60°.
∵∠BCA=∠ECD,
∴∠BCE=∠BCD+∠ECD=∠BCD+∠BCA=∠ACD=60°,B正确;
∵△ACD为等边三角形,∴∠DAC=60°.
∵∠BAC=120°,∴∠BAE=∠BAC-∠DAC=60°,
∴∠BAE=∠DAC,
∴AE平分∠BAC,故C正确.
二、13.120° 【点拨】每次旋转了360°÷3=120°.
14.(-2,-3) 15.62°
16. 【点拨】如图,连接OB,过点A作AC⊥OB交OB的延长线于点C.
∵l为OA的垂直平分线,
∴AD=OA=4,∠ADB=90°.
在Rt△ABD中,
BD===3.
由旋转可知,点A′到射线ON的距离d=AC,
∵OB·AC=OA·BD,
∴AC==.
17.(2,0) 【点拨】∵AO=AB,点A的横坐标为2,
∴OB=4,点B的坐标为(4,0),
要想让点O′,B′还在x轴上,只能左右平移.
∵点A的坐标是(2,2),移动到y轴上时,坐标变为(0,2),说明点A向左平移了2个单位长度,即横坐标减2,
∴点B也遵循点A的移动规律,则点B′的坐标是(2,0).
18.75°或255° 【点拨】如图①,当CD在OA的左侧,
CD∥AO时,旋转角为45°+30°=75°;
如图②,当CD在OA的右侧,CD∥OA时,旋转角为45°+180°+30°=255°.
三、19.解:(1)如图,线段A1B1即为所求.
(2)如图,线段A2B2即为所求.
20.解:(1)如图①所示.(答案不唯一)
(2)如图②所示.(答案不唯一)
21.解:(1)∵△ABC平移后得到△DEF,
∴∠ABC=∠E=60°.
在△ABC中,∠C=180°-∠A-∠ABC=180°-80°-60°=40°.
(2)OD=OB.理由如下:
∵AC=BC,∴∠A=∠ABC.
由平移的性质得∠A=∠EDF,
∴∠ABC=∠EDF,∴OD=OB.
22.(1)解:∵将△ABC绕点A顺时针旋转一定角度得到△ADE,∴AD=AB.
∵∠B=50°,∴∠ADF=∠B=50°.
∵AF⊥BC,
∴在Rt△ADF中,∠DAF=90°-50°=40°.
(2)证明:∵将△ABC绕点A顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上.∴∠C=∠E.
又∵∠E=∠CAD,
∴∠C=∠CAD.∴AD=CD.
23.解:(1)△ABC的面积=3×4-×3×1-×3×2-×4×1=5.5.
(2)如图,△A1B1C1即为所作.
A1(2,3),B1(5,5),C1(1,6).
(3)存在.
Q的坐标为(-1,0)或(5,0).
24.(1)证明:∵△ABC是等腰直角三角形,
∴∠ACB=90°,AC=BC,
∵CD绕着点C逆时针旋转90°到CE,
∴∠DCE=90°,CD=CE,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:∵△ABC是等腰直角三角形,
∴∠A=∠ABC=45°,
∵△ACD≌△BCE,
∴∠CBE=∠A=45°,AD=BE,
∴∠ABE=∠ABC+∠CBE=90°,
在Rt△BDE中,由勾股定理得BD2+BE2=DE2,
∴DE2=BD2+BE2=BD2+AD2=122+52=169,
∴DE=13.
一、选择题(每题3分,共36分)
1.在下面四个选项的图形中,不能由如图所示的图形经过旋转或平移得到的是( )
2.【2022·郴州】下列图形既是轴对称图形又是中心对称图形的是( )
3.如图,在平面直角坐标系中,点A,B的坐标分别为A(0,6),B(-3,-3).将线段AB平移后A点的对应点是A′(10,10),则点B的对应点B′的坐标为( )
A.(10,10)
B.(-3,-3)
C.(-3,3)
D.(7,1)
4.【2022·遵义】在平面直角坐标系中,点A(a,1)与点B(-2,b)关于原点成中心对称,则a+b的值为( )
A.-3 B.-1 C.1 D.3
5.如图,将△ABC绕点A逆时针旋转90°得到△ADE,点B,C的对应点分别为D,E,若AB=1,则BD的长为( )
A.1 B. C.2 D.2
6.如图,在平面直角坐标系xOy中,△ABC与△A1B1C1是中心对称图形.则对称中心的坐标是( )
A.(1,1) B.(1,0) C.(1,-1) D.(1,-2)
7.【2023·泰安新泰市月考】如图,△ADE与△CDB关于点D成中心对称,连接AB,以下结论错误的是( )
A.AD=CD
B.∠C=∠E
C.AE=CB
D.S△ADE=S△ADB
8.如图,△ABC的顶点都在方格线的交点(格点)上,如果将△ABC绕C点按逆时针方向旋转90°,那么点B的对应点B′的坐标是( )
A.(0,1) B.(0,-1) C.(1,0) D.(-1,0)
9. 如图是一块长方形ABCD的场地,长AB=99 m,宽AD=41 m,从A,B两处入口的路宽都为1米,两小路汇合处路口宽为2 m,其余部分种植草坪,草坪的面积为( )
A.3 783 m 2
B.3 880 m 2
C.3 920 m 2
D.4 000 m 2
10.如图,边长为3的等边三角形ABC沿BC所在直线向右平移,若平移的距离为1,则公共部分△OB′C的面积为( )
A. B. C.2 D.3
11.如图,△ABC是等边三角形,点P在△ABC内,PA=2,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )
A.2 B. C. D.1
12.【2023·济宁任城区月考】如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论不正确的是( )
A.∠ADC=60°
B.∠BCE=60°
C.AE平分∠BAC
D.AE⊥BC
二、填空题(每题3分,共18分)
13.【母题:教材P98随堂练习T1】如图所示的图案,可以看作是一个四边形(阴影部分)按顺时针方向通过3次旋转得到的,每次旋转的角度是________.
14.【2023·德州禹城市期中】如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转180°得到点P′,则点P′的坐标是________.
15.如图,射线AC,BD分别与直线l交于点A,B.现将射线AC沿直线l向右平移过点B,若∠1=46°,∠2=72°,则∠3的度数为________.
16.如图,射线OM,ON互相垂直,OA=8,点B位于射线OM的上方,且在线段OA的垂直平分线l上,连接AB,AB=5.将线段AB绕点O逆时针旋转得到线段A′B′,若点B′恰好落在射线ON上,则点A′到射线ON的距离d=________.
17.如图,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),AO=AB,将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′,B′在x轴上.则点B′的坐标是________.
18.一副三角板按如图所示叠放在一起,∠C=60°,∠OAB=45°,其中点B,D重合,若固定三角板AOB,将三角板ACD绕着公共顶点A顺时针旋转一周后停止,当旋转角为________时,CD∥AO.
三、解答题(23题12分,24题14分,其余每题10分,共66分)
19.如图,在平面直角坐标系中,线段AB的两个端点的坐标分别是A(-1,4),B(-3,1).
(1)画出线段AB向右平移4个单位长度后的线段A1B1;
(2)画出线段AB绕原点O旋转180°后的线段A2B2.
20.【母题:教材P112习题T2】如图,在6×6的网格中已经涂色了三个小正方形,请按下列要求画图.
(1)在图①中涂色一个小正方形,使涂色的四个小正方形组成一个轴对称图形.
(2)在图②中涂色一个小正方形,使涂色的四个小正方形组成一个中心对称图形.
21.如图,△ABC平移后得到△DEF.
(1)若∠A=80°,∠E=60°,求∠C的度数;
(2)若AC=BC,BC与DF相交于点O,则OD与OB相等吗?说明理由.
22.如图,在△ABC中,AF⊥BC于点F.将△ABC绕点A顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上.
(1)若∠B=50°,求∠DAF的度数;
(2)若∠E=∠CAD,求证:AD=CD.
23.△ABC在平面直角坐标系中如图所示,每个顶点都在格点上.
(1)求△ABC的面积;
(2)若△ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+3,y0+4),请画出△ABC平移后得到的△A1B1C1,并写出点A1,B1,C1的坐标;
(3)在x轴上是否存在点Q,使以A1,B,Q三点为顶点的三角形的面积为3?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
24.已知△ABC是等腰直角三角形,∠ACB=90°,点D是平面内任意一点,CD绕着点C逆时针旋转90°到CE.
(1)如图①,若D为△ABC内一点,求证:AD=BE;
(2)如图②,若D为AB边上一点,AD=5,BD=12,求DE的长.
答案
一、1.A 2.B
3.D 【点拨】由点A(0,6),A′(10,10)可知平移方式是向右平移10个单位长度,向上平移4个单位长度,∴点B(-3,-3)向右平移10个单位长度,向上平移4个单位长度得到B′(-3+10,-3+4),即(7,1).
4.C
5.B 【点拨】∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴AD=AB,∠BAD=90°,
∴△ABD是等腰直角三角形.
由勾股定理,得BD=AB.
∵AB=1,∴BD=.
6.C 【点拨】连接AA1,CC1,两线交点即为对称中心.
7.B 【点拨】∵△ADE与△CDB关于点D成中心对称,
∴AD=CD,BD=ED,AE=CB,∠E=∠CBD,
∵BD=ED,∴S△ABD=S△ADE.
8.C 【点拨】如图,可知B′的坐标为(1,0).
9.B 【点拨】(99-2)×(41-1)=97×40=3 880(平方米),
∴种植草坪面积为3 880平方米.
10.A 【点拨】如图,过点O作OH⊥BC于点H,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
由平移的性质可知BB′=1,∠A′B′C′=∠ABC=60°,
∴B′C=3-1=2,△OB′C为等边三角形,
∴OC=2,∴OH=,
∴S△OB′C=×2×=.
11.A 【点拨】∵△ABC是等边三角形,
∴AC=AB,∠CAB=60°.
∵将△PAB绕点A逆时针旋转得到△P1AC,
∴AP1=AP,∠CAP1=∠BAP,
∴∠CAB=∠CAP+∠BAP=∠CAP+∠CAP1=60°,即∠PAP1=60°,
∴△APP1是等边三角形,
∴P1P=PA=2.
12.D 【点拨】由旋转的性质可知∠EDC=∠BAC=120°,
∴当点A,D,E在同一条直线上时,∠ADC=180°-∠EDC=60°,A正确;
由旋转的性质可知△BAC≌△EDC,
∴∠BCA=∠ECD,CA=CD.
又∵∠ADC=60°,
∴△ACD为等边三角形,∴∠ACD=60°.
∵∠BCA=∠ECD,
∴∠BCE=∠BCD+∠ECD=∠BCD+∠BCA=∠ACD=60°,B正确;
∵△ACD为等边三角形,∴∠DAC=60°.
∵∠BAC=120°,∴∠BAE=∠BAC-∠DAC=60°,
∴∠BAE=∠DAC,
∴AE平分∠BAC,故C正确.
二、13.120° 【点拨】每次旋转了360°÷3=120°.
14.(-2,-3) 15.62°
16. 【点拨】如图,连接OB,过点A作AC⊥OB交OB的延长线于点C.
∵l为OA的垂直平分线,
∴AD=OA=4,∠ADB=90°.
在Rt△ABD中,
BD===3.
由旋转可知,点A′到射线ON的距离d=AC,
∵OB·AC=OA·BD,
∴AC==.
17.(2,0) 【点拨】∵AO=AB,点A的横坐标为2,
∴OB=4,点B的坐标为(4,0),
要想让点O′,B′还在x轴上,只能左右平移.
∵点A的坐标是(2,2),移动到y轴上时,坐标变为(0,2),说明点A向左平移了2个单位长度,即横坐标减2,
∴点B也遵循点A的移动规律,则点B′的坐标是(2,0).
18.75°或255° 【点拨】如图①,当CD在OA的左侧,
CD∥AO时,旋转角为45°+30°=75°;
如图②,当CD在OA的右侧,CD∥OA时,旋转角为45°+180°+30°=255°.
三、19.解:(1)如图,线段A1B1即为所求.
(2)如图,线段A2B2即为所求.
20.解:(1)如图①所示.(答案不唯一)
(2)如图②所示.(答案不唯一)
21.解:(1)∵△ABC平移后得到△DEF,
∴∠ABC=∠E=60°.
在△ABC中,∠C=180°-∠A-∠ABC=180°-80°-60°=40°.
(2)OD=OB.理由如下:
∵AC=BC,∴∠A=∠ABC.
由平移的性质得∠A=∠EDF,
∴∠ABC=∠EDF,∴OD=OB.
22.(1)解:∵将△ABC绕点A顺时针旋转一定角度得到△ADE,∴AD=AB.
∵∠B=50°,∴∠ADF=∠B=50°.
∵AF⊥BC,
∴在Rt△ADF中,∠DAF=90°-50°=40°.
(2)证明:∵将△ABC绕点A顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上.∴∠C=∠E.
又∵∠E=∠CAD,
∴∠C=∠CAD.∴AD=CD.
23.解:(1)△ABC的面积=3×4-×3×1-×3×2-×4×1=5.5.
(2)如图,△A1B1C1即为所作.
A1(2,3),B1(5,5),C1(1,6).
(3)存在.
Q的坐标为(-1,0)或(5,0).
24.(1)证明:∵△ABC是等腰直角三角形,
∴∠ACB=90°,AC=BC,
∵CD绕着点C逆时针旋转90°到CE,
∴∠DCE=90°,CD=CE,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:∵△ABC是等腰直角三角形,
∴∠A=∠ABC=45°,
∵△ACD≌△BCE,
∴∠CBE=∠A=45°,AD=BE,
∴∠ABE=∠ABC+∠CBE=90°,
在Rt△BDE中,由勾股定理得BD2+BE2=DE2,
∴DE2=BD2+BE2=BD2+AD2=122+52=169,
∴DE=13.
