鲁教版(五四学制)数学八年级上册第五章平行四边形 综合素质评价(含解析)
文档属性
| 名称 | 鲁教版(五四学制)数学八年级上册第五章平行四边形 综合素质评价(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 601.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 13:04:26 | ||
图片预览



文档简介
第五章平行四边形 综合素质评价
一、选择题(每题3分,共36分)
1.下列说法不正确的是( )
A.平行四边形两组对边分别平行
B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等
D.平行四边形的两组对边分别平行且相等
2.如图,将 ABCD的一边BC延长至点E,若∠1=80°,则∠A等于( )
A.80° B.120° C.100° D.110°
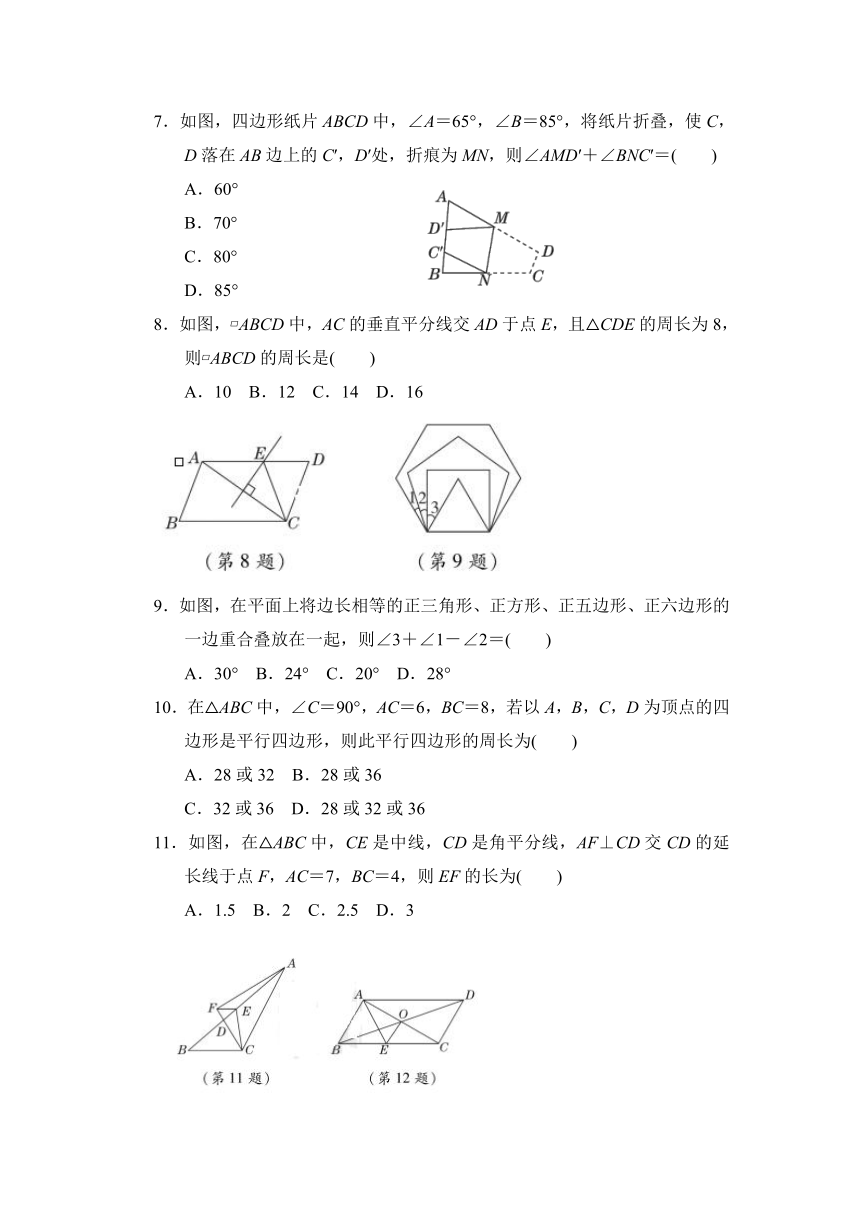
3.【2023·济南济阳区期末】一个多边形的每一个外角都是45°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
4.【2022·达州】如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF
5.【2022·大庆】如图,将 ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°,则∠A的度数为( )
A.108° B.109°
C.110° D.111°
6.已知直线a∥b,点M到直线a的距离是5 cm,到直线b的距离是3 cm,那么直线a和b之间的距离是( )
A.2 cm B.6 cm
C.8 cm D.2 cm或8 cm
7.如图,四边形纸片ABCD中,∠A=65°,∠B=85°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
A.60°
B.70°
C.80°
D.85°
8.如图, ABCD中,AC的垂直平分线交AD于点E,且△CDE的周长为8,则 ABCD的周长是( )
A.10 B.12 C.14 D.16
9.如图,在平面上将边长相等的正三角形、正方形、正五边形、正六边形的一边重合叠放在一起,则∠3+∠1-∠2=( )
A.30° B.24° C.20° D.28°
10.在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为( )
A.28或32 B.28或36
C.32或36 D.28或32或36
11.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD的延长线于点F,AC=7,BC=4,则EF的长为( )
A.1.5 B.2 C.2.5 D.3
12.【2023·济南期末】如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠ADO=30°;②S ABCD=AB·AC;③OB=AB;④S四边形OECD=S△AOD,其中成立的个数为( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每题3分,共18分)
13.【母题:教材P139随堂练习T2】【2022·南充】数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC,BC两边中点的距离DE为10 m(如图),则A,B两点的距离是________m.
14.【母题:教材P147习题T1】【2022·菏泽】如果正n边形的一个内角与一个外角的比是3∶2,则n=________.
15.如图,四边形ABCD中,AD∥BC,E是DC上一点,连接BE并延长交AD的延长线于点F,请你只添加一个条件:________________使得四边形BDFC为平行四边形.
16.【2023·济南历下区期末】如图,在 ABCD中,AC,BD相交于点O,∠ODA=90°,AC=10,BD=6,则BC的长为________.
17.如图,在正五边形ABCDE中,连接AC,BD交于点F,则∠AFB的度数为________.
18.如图①,平行四边形纸片ABCD的面积为120,AD=20.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙拼成一个轴对称图形(AD,CB重合),如图②所示,则拼成的图形中两对角线长度和为________.
三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)
19.【2022·桂林】如图,在 ABCD中,点E和点F是对角线BD上的两点,且BF=DE.
(1)求证:BE=DF;
(2)求证:△ABE≌△CDF.
20.【2023·烟台海阳市期末】如图,在△ABC中,AD是边BC的中线,F是AC上一点,且满足2AF=CF,连接BF与AD相交于点E.若G为线段BF上一动点,当点G在何位置时,四边形AFDG为平行四边形?请说明理由.
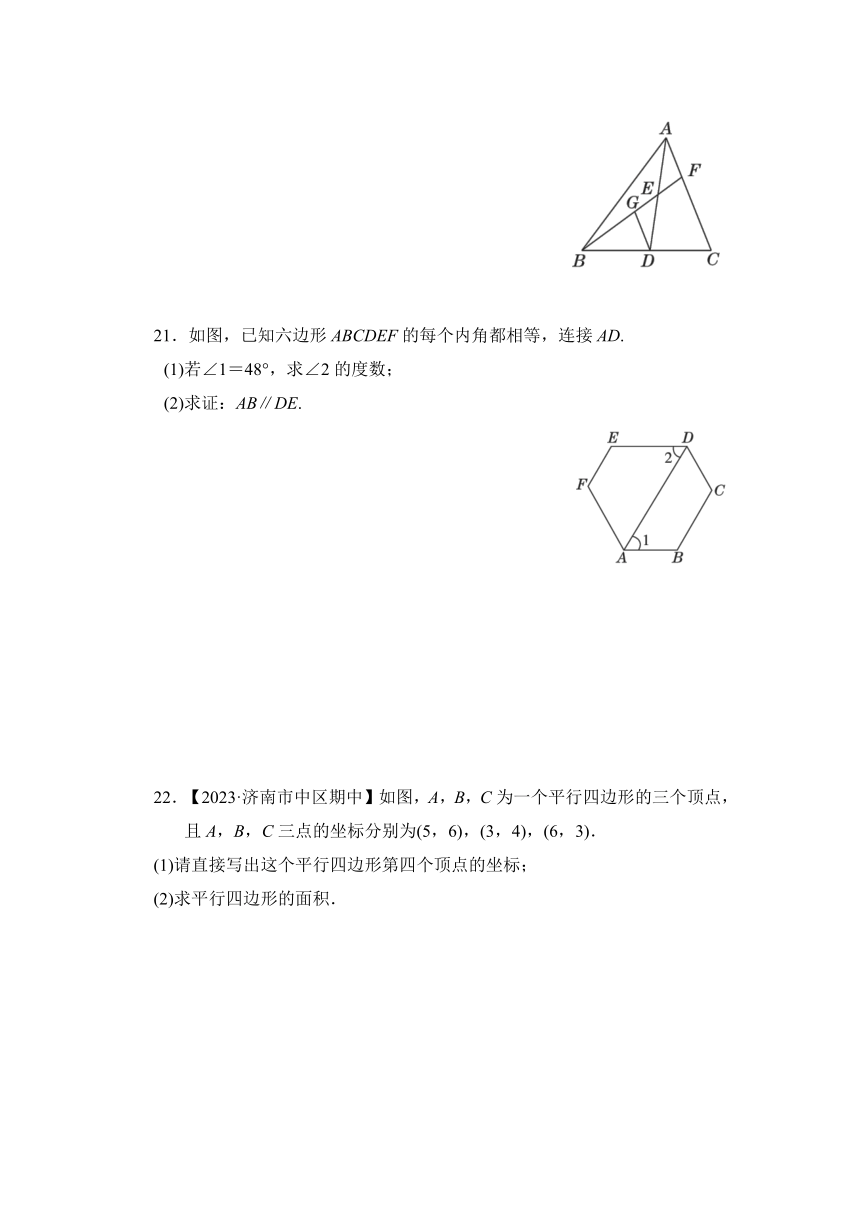
21.如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(2)求证:AB∥DE.
22.【2023·济南市中区期中】如图,A,B,C为一个平行四边形的三个顶点,且A,B,C三点的坐标分别为(5,6),(3,4),(6,3).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求平行四边形的面积.
23.如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=CF,BE与AF的交点为M,CE与DF的交点为N,连接MN,EF.
(1)求证:四边形ABFE为平行四边形;
(2)若AD=4 cm,求MN的长.
24.如图,在△ABC中,AB=AC,点D是边AB上的点,过点D作DE∥BC交AC于点E,连接BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH.
(2)当∠A为多少度时,FG⊥FH?并说明理由.
25.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②和图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=________.
答案
一、1.C 2.C 3.C 4.B
5.C 【点拨】∵四边形ABCD为平行四边形,
∴ AB∥CD,∴∠ABE=∠1=56°.
根据折叠可知∠ABD =∠EBD,
∴∠ABD =∠ABE=×56°=28°.
∵∠2=42°,
∴∠A =180°-∠ABD-∠2 =110°.
6.D 【点拨】当点M在直线a,b同侧时,直线a和b之间的距离为5-3=2(cm);
当点M在直线a,b异侧时,直线a和b之间的距离为5+3=8(cm).
7.A 【点拨】由折叠可知∠DMN=∠D′MN,
∠CNM=∠C′NM,
∵∠A+∠B+∠C+∠D=360°,∠A=65°,∠B=85°,
∴∠C+∠D=210°.
∵∠DMN+∠CNM+∠C+∠D=360°,
∴∠DMN+∠CNM=150°.
∵∠AMD′+∠BNC′+2∠DMN+2∠CNM=2×180°=360°,
∴∠AMD′+∠BNC′=60°.
8.D 【点拨】∵AC的垂直平分线交AD于点E,
∴AE=CE.
∵△CDE的周长=CD+DE+CE=CD+DE+AE=CD+AD=8,
∴ ABCD的周长=2(CD+AD)=16.故选D.
9.B 【点拨】如图.
∵正三角形、正方形、正五边形、正六边形的每个内角相等且分别为60°,90°,108°,120°,
∴∠AOE=∠1+∠2+∠3+∠DOE=120°,
∠DOE=60°,
∠2=∠BOE-∠COE=108°-90°=18°.
∴∠1+∠2+∠3=60°.
∴∠3+∠1-∠2=∠1+∠2+∠3-2∠2=60°-2×18°=24°.
10.D 【点拨】∵∠C=90°,AC=6,BC=8,
∴AB==10.
若以AC,BC为边,则平行四边形的周长=2(AC+BC)=2×(6+8)=28;
若以AC,AB为边,则平行四边形的周长=2(AC+AB)=2×(6+10)=32;
若以AB,BC为边,则平行四边形的周长=2(AB+BC)=2×(10+8)=36.
11.A 【点拨】如图,延长AF,CB交于点G.
∵CD是△ABC的角平分线,
∴∠ACF=∠BCF.
在△ACF和△GCF中,
∴△ACF≌△GCF(ASA).
∴CG=AC=7,AF=FG.
∴BG=CG-CB=3.
∵AE=EB,AF=FG,
∴EF=BG=1.5.
12.B 【点拨】∵四边形ABCD为平行四边形,∠ADC=60°,
∴OA=OC,OB=OD,∠ABC=60°,∠BAD=120°.
∵AE平分∠BAD,∴∠BAE=∠DAE=60°,
∴△ABE是等边三角形,
∴AB=AE=BE,∠AEB=60°.
∵AB=BC,∴BE=BC,
∴CE=BE=AE,∴∠ACE=∠CAE=30°,
∴∠OAB=90°,∠OAD=30°,
∴在Rt△AOB中,OB>OA,OB>AB,则③不成立;
∴OD>OA,
∴∠ADO≠∠OAD,即∠ADO≠30°,则①不成立;
∵∠OAB=90°,即AB⊥AC,
∴S ABCD=AB·AC,则②成立;
设 ABCD的面积为8a(a>0),
则S△AOD=S△COD=S△BOC=S ABCD=2a,
∵BE=CE,
∴S△BOE=S△COE=S△BOC=a,
∴S四边形OECD=S△COE+S△COD=3a=S△AOD,④成立.
综上,成立的个数为2个.
二、13.20 14.5 15.BD∥FC(答案不唯一)
16.4 【点拨】∵四边形ABCD是平行四边形,
AC=10,BD=6,
∴OA=OC=AC=5,OB=OD=BD=3.
∵∠ODA=90°,
∴AD===4,
∴BC=AD=4.
17.72° 【点拨】∵五边形ABCDE是正五边形,
∴∠BCD=∠ABC==108°,BA=BC,
∴∠BAC=∠BCA=36°.
同理∠CBD=36°,
∴∠AFB=∠BCA+∠CBD=72°.
18.26 【点拨】如图,连接EF,
则易得对角线EF⊥AD,
∵平行四边形纸片ABCD的面积为120,AD=20,
∴BC=AD=20,EF·AD=×120,
∴EF=6.
∴拼成的图形中两对角线长度和为20+6=26.
三、19.证明:(1)∵BF=DE ,
∴BF -EF=DE-EF ,即BE=DF .
(2)∵四边形ABCD是平行四边形,
∴ AB=DC,AB∥DC,
∴∠ABE=∠CDF .
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
20.解:点G为线段BF的中点时,四边形AFDG为平行四边形.理由如下:
∵AD是边BC的中线,
∴BD=CD.
∵点G为线段BF的中点,
∴DG是△BCF的中位线,
∴DG∥CF,2DG=CF,
∴DG∥AF.
∵2AF=CF,∴DG=AF,
∴四边形AFDG为平行四边形.
21.(1)解:∵六边形ABCDEF的每个内角都相等,
∴一个内角为=120°,
∴∠E=∠F=∠BAF=120°.
∵∠1=48°,
∴∠FAD=∠FAB-∠1=120°-48°=72°.
∵∠2+∠FAD+∠F+∠E=360°,
∴∠2=360°-∠FAD-∠F-∠E=360°-72°-120°-120°=48°.
(2)证明:∵∠1=120°-∠DAF,∠2=360°-120°-120°-∠DAF=
120°-∠DAF,
∴∠1=∠2,∴AB∥DE.
22.解:(1)如图,分三种情况:
当BC为对角线时,第四个顶点的坐标为(4,1);
当AB为对角线时,第四个顶点的坐标为(2,7);
当AC为对角线时,第四个顶点的坐标为(8,5).
综上所述:平行四边形第四个顶点的坐标为(2,7)或(4,1)或(8,5).
(2)∵S△ABC=3×3-×2×2-×3×1-×3×1=4,
∴S平行四边形=2S△ABC=2×4=8.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
又∵DE=CF,∴AE=BF.
∴四边形ABFE是平行四边形.
(2)解:∵DE=CF,AD∥BC,
∴四边形DEFC是平行四边形.∴DN=FN.
由(1)知四边形ABFE是平行四边形,
∴AM=MF.∴MN=AD=2 cm.
24.(1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,∴DB=EC.
∵点F,G,H分别为BE,DE,BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH.
(2)解:当∠A=90°时,FG⊥FH.
理由如下:如图,延长FG交AC于N,
∵FH是△BCE的中位线,
∴FH∥AC.
∵FG⊥FH,∴FN⊥AC,
∴∠FNC=90°.
∵FG是△EDB的中位线,
∴FG∥BD,即FN∥AB,
∴∠A=∠FNC=90°.
∴当∠A=90°时,FG⊥FH.
25.(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.∴AF=DE.
∵DF∥AC,∴∠FDB=∠C.
又∵AB=AC,∴∠B=∠C,
∴∠FDB=∠B,∴DF=BF,
∴DE+DF=AB=AC.
(2)解:图②中AC+DE=DF.
图③中AC+DF=DE.
(3)2或10
一、选择题(每题3分,共36分)
1.下列说法不正确的是( )
A.平行四边形两组对边分别平行
B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等
D.平行四边形的两组对边分别平行且相等
2.如图,将 ABCD的一边BC延长至点E,若∠1=80°,则∠A等于( )
A.80° B.120° C.100° D.110°
3.【2023·济南济阳区期末】一个多边形的每一个外角都是45°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
4.【2022·达州】如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF
5.【2022·大庆】如图,将 ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°,则∠A的度数为( )
A.108° B.109°
C.110° D.111°
6.已知直线a∥b,点M到直线a的距离是5 cm,到直线b的距离是3 cm,那么直线a和b之间的距离是( )
A.2 cm B.6 cm
C.8 cm D.2 cm或8 cm
7.如图,四边形纸片ABCD中,∠A=65°,∠B=85°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
A.60°
B.70°
C.80°
D.85°
8.如图, ABCD中,AC的垂直平分线交AD于点E,且△CDE的周长为8,则 ABCD的周长是( )
A.10 B.12 C.14 D.16
9.如图,在平面上将边长相等的正三角形、正方形、正五边形、正六边形的一边重合叠放在一起,则∠3+∠1-∠2=( )
A.30° B.24° C.20° D.28°
10.在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为( )
A.28或32 B.28或36
C.32或36 D.28或32或36
11.如图,在△ABC中,CE是中线,CD是角平分线,AF⊥CD交CD的延长线于点F,AC=7,BC=4,则EF的长为( )
A.1.5 B.2 C.2.5 D.3
12.【2023·济南期末】如图, ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠ADO=30°;②S ABCD=AB·AC;③OB=AB;④S四边形OECD=S△AOD,其中成立的个数为( )
A.1个
B.2个
C.3个
D.4个
二、填空题(每题3分,共18分)
13.【母题:教材P139随堂练习T2】【2022·南充】数学实践活动中,为了测量校园内被花坛隔开的A,B两点的距离,同学们在AB外选择一点C,测得AC,BC两边中点的距离DE为10 m(如图),则A,B两点的距离是________m.
14.【母题:教材P147习题T1】【2022·菏泽】如果正n边形的一个内角与一个外角的比是3∶2,则n=________.
15.如图,四边形ABCD中,AD∥BC,E是DC上一点,连接BE并延长交AD的延长线于点F,请你只添加一个条件:________________使得四边形BDFC为平行四边形.
16.【2023·济南历下区期末】如图,在 ABCD中,AC,BD相交于点O,∠ODA=90°,AC=10,BD=6,则BC的长为________.
17.如图,在正五边形ABCDE中,连接AC,BD交于点F,则∠AFB的度数为________.
18.如图①,平行四边形纸片ABCD的面积为120,AD=20.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙拼成一个轴对称图形(AD,CB重合),如图②所示,则拼成的图形中两对角线长度和为________.
三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)
19.【2022·桂林】如图,在 ABCD中,点E和点F是对角线BD上的两点,且BF=DE.
(1)求证:BE=DF;
(2)求证:△ABE≌△CDF.
20.【2023·烟台海阳市期末】如图,在△ABC中,AD是边BC的中线,F是AC上一点,且满足2AF=CF,连接BF与AD相交于点E.若G为线段BF上一动点,当点G在何位置时,四边形AFDG为平行四边形?请说明理由.
21.如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1=48°,求∠2的度数;
(2)求证:AB∥DE.
22.【2023·济南市中区期中】如图,A,B,C为一个平行四边形的三个顶点,且A,B,C三点的坐标分别为(5,6),(3,4),(6,3).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求平行四边形的面积.
23.如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=CF,BE与AF的交点为M,CE与DF的交点为N,连接MN,EF.
(1)求证:四边形ABFE为平行四边形;
(2)若AD=4 cm,求MN的长.
24.如图,在△ABC中,AB=AC,点D是边AB上的点,过点D作DE∥BC交AC于点E,连接BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH.
(2)当∠A为多少度时,FG⊥FH?并说明理由.
25.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②和图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=________.
答案
一、1.C 2.C 3.C 4.B
5.C 【点拨】∵四边形ABCD为平行四边形,
∴ AB∥CD,∴∠ABE=∠1=56°.
根据折叠可知∠ABD =∠EBD,
∴∠ABD =∠ABE=×56°=28°.
∵∠2=42°,
∴∠A =180°-∠ABD-∠2 =110°.
6.D 【点拨】当点M在直线a,b同侧时,直线a和b之间的距离为5-3=2(cm);
当点M在直线a,b异侧时,直线a和b之间的距离为5+3=8(cm).
7.A 【点拨】由折叠可知∠DMN=∠D′MN,
∠CNM=∠C′NM,
∵∠A+∠B+∠C+∠D=360°,∠A=65°,∠B=85°,
∴∠C+∠D=210°.
∵∠DMN+∠CNM+∠C+∠D=360°,
∴∠DMN+∠CNM=150°.
∵∠AMD′+∠BNC′+2∠DMN+2∠CNM=2×180°=360°,
∴∠AMD′+∠BNC′=60°.
8.D 【点拨】∵AC的垂直平分线交AD于点E,
∴AE=CE.
∵△CDE的周长=CD+DE+CE=CD+DE+AE=CD+AD=8,
∴ ABCD的周长=2(CD+AD)=16.故选D.
9.B 【点拨】如图.
∵正三角形、正方形、正五边形、正六边形的每个内角相等且分别为60°,90°,108°,120°,
∴∠AOE=∠1+∠2+∠3+∠DOE=120°,
∠DOE=60°,
∠2=∠BOE-∠COE=108°-90°=18°.
∴∠1+∠2+∠3=60°.
∴∠3+∠1-∠2=∠1+∠2+∠3-2∠2=60°-2×18°=24°.
10.D 【点拨】∵∠C=90°,AC=6,BC=8,
∴AB==10.
若以AC,BC为边,则平行四边形的周长=2(AC+BC)=2×(6+8)=28;
若以AC,AB为边,则平行四边形的周长=2(AC+AB)=2×(6+10)=32;
若以AB,BC为边,则平行四边形的周长=2(AB+BC)=2×(10+8)=36.
11.A 【点拨】如图,延长AF,CB交于点G.
∵CD是△ABC的角平分线,
∴∠ACF=∠BCF.
在△ACF和△GCF中,
∴△ACF≌△GCF(ASA).
∴CG=AC=7,AF=FG.
∴BG=CG-CB=3.
∵AE=EB,AF=FG,
∴EF=BG=1.5.
12.B 【点拨】∵四边形ABCD为平行四边形,∠ADC=60°,
∴OA=OC,OB=OD,∠ABC=60°,∠BAD=120°.
∵AE平分∠BAD,∴∠BAE=∠DAE=60°,
∴△ABE是等边三角形,
∴AB=AE=BE,∠AEB=60°.
∵AB=BC,∴BE=BC,
∴CE=BE=AE,∴∠ACE=∠CAE=30°,
∴∠OAB=90°,∠OAD=30°,
∴在Rt△AOB中,OB>OA,OB>AB,则③不成立;
∴OD>OA,
∴∠ADO≠∠OAD,即∠ADO≠30°,则①不成立;
∵∠OAB=90°,即AB⊥AC,
∴S ABCD=AB·AC,则②成立;
设 ABCD的面积为8a(a>0),
则S△AOD=S△COD=S△BOC=S ABCD=2a,
∵BE=CE,
∴S△BOE=S△COE=S△BOC=a,
∴S四边形OECD=S△COE+S△COD=3a=S△AOD,④成立.
综上,成立的个数为2个.
二、13.20 14.5 15.BD∥FC(答案不唯一)
16.4 【点拨】∵四边形ABCD是平行四边形,
AC=10,BD=6,
∴OA=OC=AC=5,OB=OD=BD=3.
∵∠ODA=90°,
∴AD===4,
∴BC=AD=4.
17.72° 【点拨】∵五边形ABCDE是正五边形,
∴∠BCD=∠ABC==108°,BA=BC,
∴∠BAC=∠BCA=36°.
同理∠CBD=36°,
∴∠AFB=∠BCA+∠CBD=72°.
18.26 【点拨】如图,连接EF,
则易得对角线EF⊥AD,
∵平行四边形纸片ABCD的面积为120,AD=20,
∴BC=AD=20,EF·AD=×120,
∴EF=6.
∴拼成的图形中两对角线长度和为20+6=26.
三、19.证明:(1)∵BF=DE ,
∴BF -EF=DE-EF ,即BE=DF .
(2)∵四边形ABCD是平行四边形,
∴ AB=DC,AB∥DC,
∴∠ABE=∠CDF .
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
20.解:点G为线段BF的中点时,四边形AFDG为平行四边形.理由如下:
∵AD是边BC的中线,
∴BD=CD.
∵点G为线段BF的中点,
∴DG是△BCF的中位线,
∴DG∥CF,2DG=CF,
∴DG∥AF.
∵2AF=CF,∴DG=AF,
∴四边形AFDG为平行四边形.
21.(1)解:∵六边形ABCDEF的每个内角都相等,
∴一个内角为=120°,
∴∠E=∠F=∠BAF=120°.
∵∠1=48°,
∴∠FAD=∠FAB-∠1=120°-48°=72°.
∵∠2+∠FAD+∠F+∠E=360°,
∴∠2=360°-∠FAD-∠F-∠E=360°-72°-120°-120°=48°.
(2)证明:∵∠1=120°-∠DAF,∠2=360°-120°-120°-∠DAF=
120°-∠DAF,
∴∠1=∠2,∴AB∥DE.
22.解:(1)如图,分三种情况:
当BC为对角线时,第四个顶点的坐标为(4,1);
当AB为对角线时,第四个顶点的坐标为(2,7);
当AC为对角线时,第四个顶点的坐标为(8,5).
综上所述:平行四边形第四个顶点的坐标为(2,7)或(4,1)或(8,5).
(2)∵S△ABC=3×3-×2×2-×3×1-×3×1=4,
∴S平行四边形=2S△ABC=2×4=8.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
又∵DE=CF,∴AE=BF.
∴四边形ABFE是平行四边形.
(2)解:∵DE=CF,AD∥BC,
∴四边形DEFC是平行四边形.∴DN=FN.
由(1)知四边形ABFE是平行四边形,
∴AM=MF.∴MN=AD=2 cm.
24.(1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,∴DB=EC.
∵点F,G,H分别为BE,DE,BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FG=BD,FH=CE,
∴FG=FH.
(2)解:当∠A=90°时,FG⊥FH.
理由如下:如图,延长FG交AC于N,
∵FH是△BCE的中位线,
∴FH∥AC.
∵FG⊥FH,∴FN⊥AC,
∴∠FNC=90°.
∵FG是△EDB的中位线,
∴FG∥BD,即FN∥AB,
∴∠A=∠FNC=90°.
∴当∠A=90°时,FG⊥FH.
25.(1)证明:∵DF∥AC,DE∥AB,
∴四边形AFDE是平行四边形.∴AF=DE.
∵DF∥AC,∴∠FDB=∠C.
又∵AB=AC,∴∠B=∠C,
∴∠FDB=∠B,∴DF=BF,
∴DE+DF=AB=AC.
(2)解:图②中AC+DE=DF.
图③中AC+DF=DE.
(3)2或10
