鲁教版(五四学制)数学八年级上册期末综合素质评价(二)(含解析)
文档属性
| 名称 | 鲁教版(五四学制)数学八年级上册期末综合素质评价(二)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 481.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 13:05:59 | ||
图片预览




文档简介
鲁教版数学八年级上册期末综合素质评价(二)
一、选择题(每题3分,共36分)
1.下列各组图形可以通过平移得到的是( )
2.【数学文化】剪纸是我国具有独特艺术风格的民间艺术,反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中,是中心对称图形的有( )
A.①②③ B.①②④ C.①③④ D.②③④
3.下列分式是最简分式的是( )
A. B. C. D.
4.一个多边形的内角和与外角和相加之后的结果是2 520°,则这个多边形的边数为( )
A.12 B.13 C.14 D.15
5.【2022·济南历下区期中】某单位招聘大堂经理,考核项目为个人形象、交际能力、专业知识三个项目,且权重之比为2∶3∶5,应聘者高颖三个方面的得分依次为80分、90分、80分,则她的最终得分为( )
A.79分 B.83分 C.85分 D.87分
6.【2023·淄博张店区月考】下列因式分解正确的是( )
A.a2+b2=(a+b)2
B.5m2-20mn=m(5m-20n)
C.-x2+y2=(y-x)(x+y)
D.a3-a=a(a2-1)
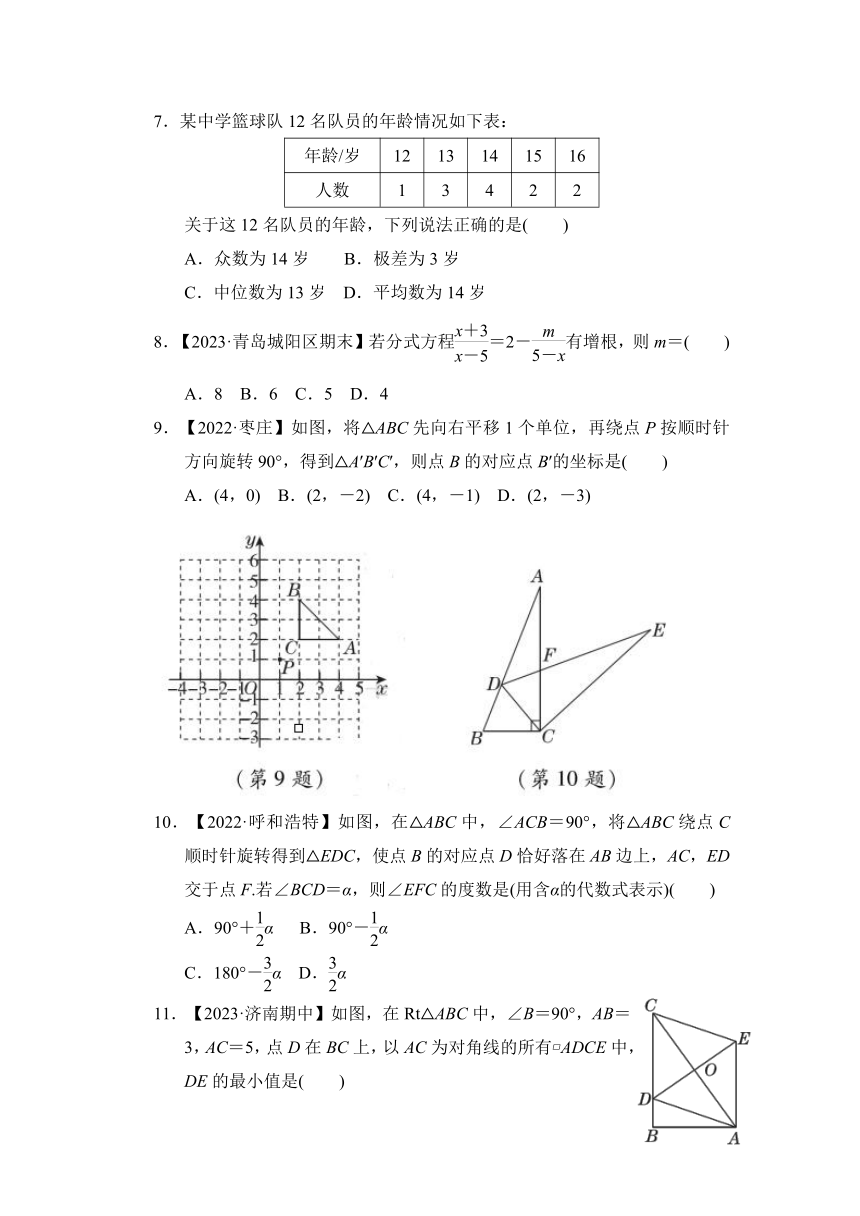
7.某中学篮球队12名队员的年龄情况如下表:
年龄/岁 12 13 14 15 16
人数 1 3 4 2 2
关于这12名队员的年龄,下列说法正确的是( )
A.众数为14岁 B.极差为3岁
C.中位数为13岁 D.平均数为14岁
8.【2023·青岛城阳区期末】若分式方程=2-有增根,则m=( )
A.8 B.6 C.5 D.4
9.【2022·枣庄】如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
A.(4,0) B.(2,-2) C.(4,-1) D.(2,-3)
10.【2022·呼和浩特】如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△EDC,使点B的对应点D恰好落在AB边上,AC,ED交于点F.若∠BCD=α,则∠EFC的度数是(用含α的代数式表示)( )
A.90°+α B.90°-α
C.180°-α D.α
11.【2023·济南期中】如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点D在BC上,以AC为对角线的所有 ADCE中,DE的最小值是( )
A.3 B.4
C.2 D.1
12. 【2023·烟台龙口市期末】如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBnCn的周长为( )
A.a B.a C.a D.a
二、填空题(每题3分,共18分)
13.【2022·赤峰】分解因式:2x3+4x2+2x=________.
14.【2023·泰安新泰市月考】当x=________时,分式的值为0.
15.如果一组数据的方差s=×[(x1-20)2+(x2-20)2+…+(x12-20)2],已知9是这组数据中的一个数据,现把9去掉,所得新的一组数据的平均数是________.
16.【2023·青岛市北区期中】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位长度后,得到△A′B′C′,连接A′C,则△A′B′C的周长为________________________________________.
17.如图, ABCD绕点A逆时针旋转32°,得到 AB′C′D′,点B′恰好落在BC边上,B′C′和CD交于点P,则∠B′PC的度数是________.
18.若关于x的分式方程=+2的解为正数,则m的取值范围是______________.
三、解答题(19题6分,20,22,24题每题8分,其余每题12分,共66分)
19.已知a,b,c为△ABC的三边长,求证:(a-c)2-b2是负数.
20.先化简,再求值:
(1)【2023·淄博高青县期中】÷,其中x=;
(2)÷,其中x满足x2-2x-2=0.
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,0),B(-4,1),C(-2,2).
(1)点B关于原点对称的点B′的坐标是________;
(2)平移△ABC,使平移后点A的对应点A1的坐标为(2,1),请画出平移后的△A1B1C1;
(3)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2.
22.【2022·丹东】为推动家乡学校篮球运动的发展,某公司计划出资12 000元购买一批篮球赠送给家乡的学校.实际购买时,每个篮球的价格比原价降低了20元,结果该公司出资10 000元就购买了和原计划一样多的篮球,每个篮球的原价是多少元?
23.【母题:教材P149复习题T7】如图,E,F分别是 ABCD的边AD,BC的中点.
(1)求证:BE=DF;
(2)连接AF,EC,分别交BE,DF于点M,N,判断四边形MFNE是不是平行四边形,说明理由.
24.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A按顺时针方向旋转60°得到△AB′C′,连接C′B,求:
(1)∠ABC′的度数;
(2)C′B的长.
25.【2022·襄阳】在“双减”背景下,某区教育部门想了解该区A,B两所学校九年级各500名学生的课后书面作业时长情况,从这两所学校分别随机抽取50名九年级学生的课后书面作业时长数据(保留整数),整理分析过程如下:
【收集数据】A学校50名九年级学生中,课后书面作业时长在70.5≤x<80.5组的具体数据如下:(单位:分钟)
74,72,72,73,74,75,75,75,75,
75,75,76,76,76,77,77,78,80.
【整理数据】不完整的两所学校的频数分布表如下,不完整的A学校频数直方图如图所示:
组别 50.5≤x<60.5 60.5≤x<70.5 70.5≤x<80.5 80.5≤x<90.5 90.5≤x<100.5
A学校 5 15 a 8 4
B学校 7 10 12 17 4
【分析数据】两组数据的平均数、众数、中位数、方差如下表:
特征数 平均数 众数 中位数 方差
A学校 74 75 b 127.36
B学校 74 85 73 144.12
根据以上信息,回答下列问题:
(1)本次调查是________调查(填“抽样”或“全面”);
(2)统计表中a=________,b=________;
(3)补全频数直方图;
(4)在这次调查中,课后书面作业时长波动较小的是______学校(填“A”或“B”);
(5)按规定,九年级学生每天课后书面作业时长不得超过90分钟,估计两所学校1 000名学生中,能在90分钟内(包括90分钟)完成当日课后书面作业的学生共有________人.
答案
一、1.C 2.A 3.D 4.C 5.B 6.C 7.A
8.A 【点拨】 =2-,
去分母,得x+3=2(x-5)+m,
解得x=13-m,
∵分式方程有增根,
∴x-5=0,∴x=5.
把x=5代入x=13-m,
得5=13-m,解得m=8.
9.C 【点拨】作出旋转后的图形如图.
∴点B′的坐标为(4,-1).
10.C 【点拨】由旋转的性质可知BC=CD,∠B=∠EDC,∠A=∠E,∠ACE=∠BCD.
∵∠BCD=α,
∴∠B=∠BDC==90°-,∠ACE=α.
∵∠ACB=90°,
∴∠A=90°-∠B=.∴∠E=.
∴∠EFC=180°-∠ECF-∠E=180°-α.
11.A 【点拨】∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,线段DE最短,此时OD⊥BC.
∴OD∥AB.
∵BD∥AE,∴四边形ABDE是平行四边形,
∴DE=AB=3.
12.A 【点拨】∵点A1,B1,C1分别为BC,AC,AB的中点,
∴B1C1=BC,A1C1=AC,A1B1=AB,
∴△A1B1C1的周长=a,
同理,△A2B2C2的周长=a=a,…
∴△AnBnCn的周长=a.
二、13.2x(x+1)2
14.-3 【点拨】∵分式的值为0,
∴
由①得x=±3,由②得x≠-2且x≠3,
∴x=-3.
15.21 【点拨】由题意知新的一组数据的平均数是(20×12-9)÷11=21.
16.12 【点拨】∵△ABC沿射线BC方向平移2个单位长度后,得到△A′B′C′,
∴BB′=2,A′B′=AB=4,∠A′B′C′=∠B=60°,
∴B′C=BC-BB′=6-2=4,
∴A′B′=B′C,
∴△A′B′C为等边三角形,
∴△A′B′C的周长=3B′C=12.
17.42° 【点拨】∵ ABCD绕点A逆时针旋转32°,得到 AB′C′D′,
∴AB=AB′,∠BAB′=32°,∠ABC=∠AB′C′,∠B+∠C=180°,
∴∠B=∠AB′B=74°,
∴∠C=106°,∠AB′C′=∠B=74°,
∴∠CB′P=32°,
∴∠B′PC=180°-∠C-∠CB′P=180°-106°-32°=42°.
18.m<-2且m≠-3 【点拨】去分母,得3x=-m+2(x-1),
去括号、移项、合并同类项,得
x=-m-2.
∵关于x的分式方程=+2的解为正数,
∴-m-2>0.∴m<-2.
由题意得x-1≠0,∴x≠1.∴-m-2≠1.
∴m≠-3.∴m<-2且m≠-3.
三、19.证明:∵a,b,c为△ABC的三边长,
∴a+b>c,b+c>a,
即a-c+b>0,a-c-b<0.
∴(a-c)2-b2=(a-c+b)(a-c-b)<0,
∴(a-c)2-b2是负数.
20.解:(1)原式=·
=
=,
当x=时,原式===-.
(2)原式=·
=·
=·
=.
∵x2-2x-2=0,
∴x2=2x+2=2(x+1),
∴原式==.
21.解:(1)(4,-1)
(2)如图,△A1B1C1即为所求.
(3)如图,△A2B2C2即为所求.
22.解:设每个篮球的原价是x元,则每个篮球的实际价格是(x-20)元,
根据题意,得=.解得x=120.
经检验x=120是原方程的根.
答:每个篮球的原价是120元.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵E,F分别是 ABCD的边AD,BC的中点,
∴DE=AD,BF=BC,
∴DE=BF.
∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
(2)解:四边形MFNE是平行四边形.理由如下:
如图,由(1)得四边形BEDF是平行四边形,
∴BE∥DF.
同理:四边形AECF是平行四边形,
∴AF∥EC,
∴四边形MFNE是平行四边形.
24.解:(1)连接BB′,
由题意,得AC′=B′C′,∠BAB′=60°,BA=B′A,
∴△ABB′为等边三角形.
∴∠ABB′=60°,AB=B′B.
在△ABC′和△B′BC′中,
∴△ABC′≌△B′BC′(SSS).
∴∠ABC′=∠B′BC′=30°.
(2)延长BC′交AB′于点M.
∵AB=B′B,∠MBB′=∠MBA.
∴BM⊥AB′,且AM=B′M.
在Rt△ABC中,∠C=90°,AC=BC=,
∴AB==2.
∴AB′=AB=2.
∴AM=1.
∴易得C′M=AM=1.
在Rt△ABM中,AM=1,AB=2,
∴BM==,
∴C′B=BM-C′M=-1.
25.解:(1)抽样
(2)18;74.5
(3)补全频数直方图如图.
(4)A
(5)920
一、选择题(每题3分,共36分)
1.下列各组图形可以通过平移得到的是( )
2.【数学文化】剪纸是我国具有独特艺术风格的民间艺术,反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中,是中心对称图形的有( )
A.①②③ B.①②④ C.①③④ D.②③④
3.下列分式是最简分式的是( )
A. B. C. D.
4.一个多边形的内角和与外角和相加之后的结果是2 520°,则这个多边形的边数为( )
A.12 B.13 C.14 D.15
5.【2022·济南历下区期中】某单位招聘大堂经理,考核项目为个人形象、交际能力、专业知识三个项目,且权重之比为2∶3∶5,应聘者高颖三个方面的得分依次为80分、90分、80分,则她的最终得分为( )
A.79分 B.83分 C.85分 D.87分
6.【2023·淄博张店区月考】下列因式分解正确的是( )
A.a2+b2=(a+b)2
B.5m2-20mn=m(5m-20n)
C.-x2+y2=(y-x)(x+y)
D.a3-a=a(a2-1)
7.某中学篮球队12名队员的年龄情况如下表:
年龄/岁 12 13 14 15 16
人数 1 3 4 2 2
关于这12名队员的年龄,下列说法正确的是( )
A.众数为14岁 B.极差为3岁
C.中位数为13岁 D.平均数为14岁
8.【2023·青岛城阳区期末】若分式方程=2-有增根,则m=( )
A.8 B.6 C.5 D.4
9.【2022·枣庄】如图,将△ABC先向右平移1个单位,再绕点P按顺时针方向旋转90°,得到△A′B′C′,则点B的对应点B′的坐标是( )
A.(4,0) B.(2,-2) C.(4,-1) D.(2,-3)
10.【2022·呼和浩特】如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△EDC,使点B的对应点D恰好落在AB边上,AC,ED交于点F.若∠BCD=α,则∠EFC的度数是(用含α的代数式表示)( )
A.90°+α B.90°-α
C.180°-α D.α
11.【2023·济南期中】如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点D在BC上,以AC为对角线的所有 ADCE中,DE的最小值是( )
A.3 B.4
C.2 D.1
12. 【2023·烟台龙口市期末】如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBnCn的周长为( )
A.a B.a C.a D.a
二、填空题(每题3分,共18分)
13.【2022·赤峰】分解因式:2x3+4x2+2x=________.
14.【2023·泰安新泰市月考】当x=________时,分式的值为0.
15.如果一组数据的方差s=×[(x1-20)2+(x2-20)2+…+(x12-20)2],已知9是这组数据中的一个数据,现把9去掉,所得新的一组数据的平均数是________.
16.【2023·青岛市北区期中】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC方向平移2个单位长度后,得到△A′B′C′,连接A′C,则△A′B′C的周长为________________________________________.
17.如图, ABCD绕点A逆时针旋转32°,得到 AB′C′D′,点B′恰好落在BC边上,B′C′和CD交于点P,则∠B′PC的度数是________.
18.若关于x的分式方程=+2的解为正数,则m的取值范围是______________.
三、解答题(19题6分,20,22,24题每题8分,其余每题12分,共66分)
19.已知a,b,c为△ABC的三边长,求证:(a-c)2-b2是负数.
20.先化简,再求值:
(1)【2023·淄博高青县期中】÷,其中x=;
(2)÷,其中x满足x2-2x-2=0.
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,0),B(-4,1),C(-2,2).
(1)点B关于原点对称的点B′的坐标是________;
(2)平移△ABC,使平移后点A的对应点A1的坐标为(2,1),请画出平移后的△A1B1C1;
(3)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2.
22.【2022·丹东】为推动家乡学校篮球运动的发展,某公司计划出资12 000元购买一批篮球赠送给家乡的学校.实际购买时,每个篮球的价格比原价降低了20元,结果该公司出资10 000元就购买了和原计划一样多的篮球,每个篮球的原价是多少元?
23.【母题:教材P149复习题T7】如图,E,F分别是 ABCD的边AD,BC的中点.
(1)求证:BE=DF;
(2)连接AF,EC,分别交BE,DF于点M,N,判断四边形MFNE是不是平行四边形,说明理由.
24.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A按顺时针方向旋转60°得到△AB′C′,连接C′B,求:
(1)∠ABC′的度数;
(2)C′B的长.
25.【2022·襄阳】在“双减”背景下,某区教育部门想了解该区A,B两所学校九年级各500名学生的课后书面作业时长情况,从这两所学校分别随机抽取50名九年级学生的课后书面作业时长数据(保留整数),整理分析过程如下:
【收集数据】A学校50名九年级学生中,课后书面作业时长在70.5≤x<80.5组的具体数据如下:(单位:分钟)
74,72,72,73,74,75,75,75,75,
75,75,76,76,76,77,77,78,80.
【整理数据】不完整的两所学校的频数分布表如下,不完整的A学校频数直方图如图所示:
组别 50.5≤x<60.5 60.5≤x<70.5 70.5≤x<80.5 80.5≤x<90.5 90.5≤x<100.5
A学校 5 15 a 8 4
B学校 7 10 12 17 4
【分析数据】两组数据的平均数、众数、中位数、方差如下表:
特征数 平均数 众数 中位数 方差
A学校 74 75 b 127.36
B学校 74 85 73 144.12
根据以上信息,回答下列问题:
(1)本次调查是________调查(填“抽样”或“全面”);
(2)统计表中a=________,b=________;
(3)补全频数直方图;
(4)在这次调查中,课后书面作业时长波动较小的是______学校(填“A”或“B”);
(5)按规定,九年级学生每天课后书面作业时长不得超过90分钟,估计两所学校1 000名学生中,能在90分钟内(包括90分钟)完成当日课后书面作业的学生共有________人.
答案
一、1.C 2.A 3.D 4.C 5.B 6.C 7.A
8.A 【点拨】 =2-,
去分母,得x+3=2(x-5)+m,
解得x=13-m,
∵分式方程有增根,
∴x-5=0,∴x=5.
把x=5代入x=13-m,
得5=13-m,解得m=8.
9.C 【点拨】作出旋转后的图形如图.
∴点B′的坐标为(4,-1).
10.C 【点拨】由旋转的性质可知BC=CD,∠B=∠EDC,∠A=∠E,∠ACE=∠BCD.
∵∠BCD=α,
∴∠B=∠BDC==90°-,∠ACE=α.
∵∠ACB=90°,
∴∠A=90°-∠B=.∴∠E=.
∴∠EFC=180°-∠ECF-∠E=180°-α.
11.A 【点拨】∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,线段DE最短,此时OD⊥BC.
∴OD∥AB.
∵BD∥AE,∴四边形ABDE是平行四边形,
∴DE=AB=3.
12.A 【点拨】∵点A1,B1,C1分别为BC,AC,AB的中点,
∴B1C1=BC,A1C1=AC,A1B1=AB,
∴△A1B1C1的周长=a,
同理,△A2B2C2的周长=a=a,…
∴△AnBnCn的周长=a.
二、13.2x(x+1)2
14.-3 【点拨】∵分式的值为0,
∴
由①得x=±3,由②得x≠-2且x≠3,
∴x=-3.
15.21 【点拨】由题意知新的一组数据的平均数是(20×12-9)÷11=21.
16.12 【点拨】∵△ABC沿射线BC方向平移2个单位长度后,得到△A′B′C′,
∴BB′=2,A′B′=AB=4,∠A′B′C′=∠B=60°,
∴B′C=BC-BB′=6-2=4,
∴A′B′=B′C,
∴△A′B′C为等边三角形,
∴△A′B′C的周长=3B′C=12.
17.42° 【点拨】∵ ABCD绕点A逆时针旋转32°,得到 AB′C′D′,
∴AB=AB′,∠BAB′=32°,∠ABC=∠AB′C′,∠B+∠C=180°,
∴∠B=∠AB′B=74°,
∴∠C=106°,∠AB′C′=∠B=74°,
∴∠CB′P=32°,
∴∠B′PC=180°-∠C-∠CB′P=180°-106°-32°=42°.
18.m<-2且m≠-3 【点拨】去分母,得3x=-m+2(x-1),
去括号、移项、合并同类项,得
x=-m-2.
∵关于x的分式方程=+2的解为正数,
∴-m-2>0.∴m<-2.
由题意得x-1≠0,∴x≠1.∴-m-2≠1.
∴m≠-3.∴m<-2且m≠-3.
三、19.证明:∵a,b,c为△ABC的三边长,
∴a+b>c,b+c>a,
即a-c+b>0,a-c-b<0.
∴(a-c)2-b2=(a-c+b)(a-c-b)<0,
∴(a-c)2-b2是负数.
20.解:(1)原式=·
=
=,
当x=时,原式===-.
(2)原式=·
=·
=·
=.
∵x2-2x-2=0,
∴x2=2x+2=2(x+1),
∴原式==.
21.解:(1)(4,-1)
(2)如图,△A1B1C1即为所求.
(3)如图,△A2B2C2即为所求.
22.解:设每个篮球的原价是x元,则每个篮球的实际价格是(x-20)元,
根据题意,得=.解得x=120.
经检验x=120是原方程的根.
答:每个篮球的原价是120元.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵E,F分别是 ABCD的边AD,BC的中点,
∴DE=AD,BF=BC,
∴DE=BF.
∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE=DF.
(2)解:四边形MFNE是平行四边形.理由如下:
如图,由(1)得四边形BEDF是平行四边形,
∴BE∥DF.
同理:四边形AECF是平行四边形,
∴AF∥EC,
∴四边形MFNE是平行四边形.
24.解:(1)连接BB′,
由题意,得AC′=B′C′,∠BAB′=60°,BA=B′A,
∴△ABB′为等边三角形.
∴∠ABB′=60°,AB=B′B.
在△ABC′和△B′BC′中,
∴△ABC′≌△B′BC′(SSS).
∴∠ABC′=∠B′BC′=30°.
(2)延长BC′交AB′于点M.
∵AB=B′B,∠MBB′=∠MBA.
∴BM⊥AB′,且AM=B′M.
在Rt△ABC中,∠C=90°,AC=BC=,
∴AB==2.
∴AB′=AB=2.
∴AM=1.
∴易得C′M=AM=1.
在Rt△ABM中,AM=1,AB=2,
∴BM==,
∴C′B=BM-C′M=-1.
25.解:(1)抽样
(2)18;74.5
(3)补全频数直方图如图.
(4)A
(5)920
同课章节目录
