生物人教版(2019)选择性必修2 1.2种群数量的变化(共26张ppt)
文档属性
| 名称 | 生物人教版(2019)选择性必修2 1.2种群数量的变化(共26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2023-06-18 07:47:54 | ||
图片预览



文档简介
(共26张PPT)
种群的数量增长
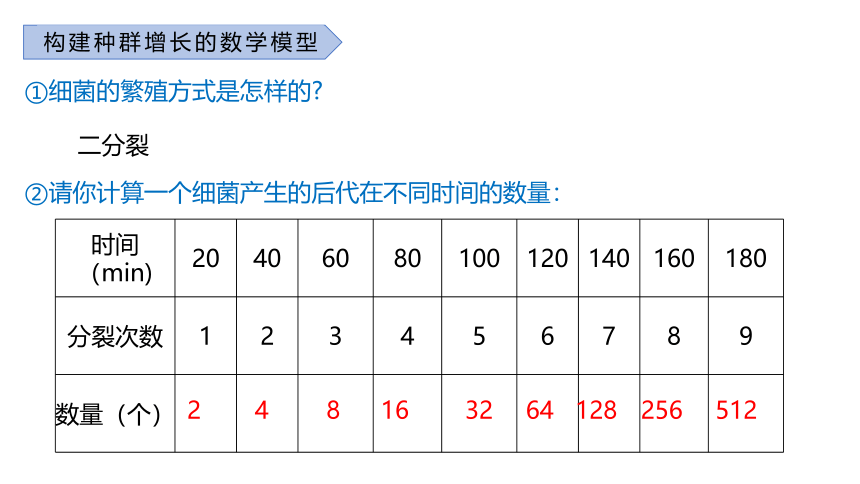
时间(min) 20 40 60 80 100 120 140 160 180
分裂次数 1 2 3 4 5 6 7 8 9
数量(个)
2
4
8
16
32
64
128
256
512
①细菌的繁殖方式是怎样的
二分裂
②请你计算一个细菌产生的后代在不同时间的数量:
构建种群增长的数学模型
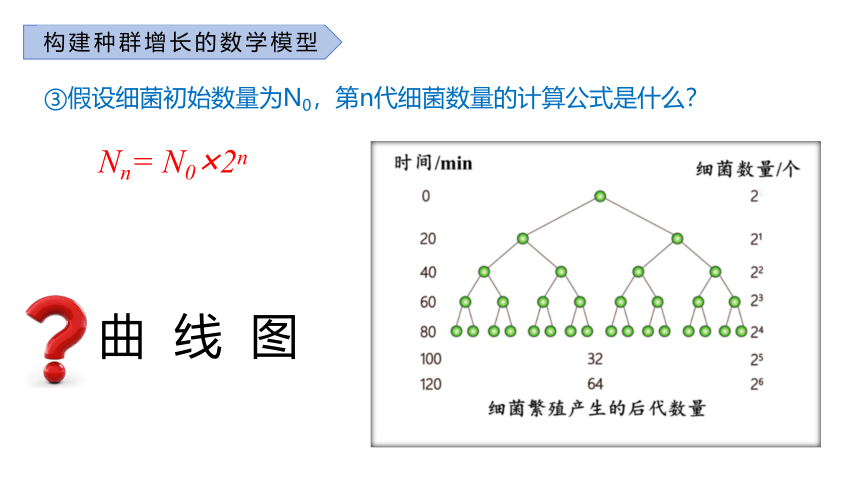
③假设细菌初始数量为N0,第n代细菌数量的计算公式是什么?
Nn= N0×2n
曲线图
构建种群增长的数学模型
构建种群增长的数学模型
以 为横坐标
以 为纵坐标
时间
细菌数量
0 20 40 60 80 100 120 140
551
501
451
401
351
201
151
51
1
时间/min
细菌数量/个
构建种群增长的数学模型
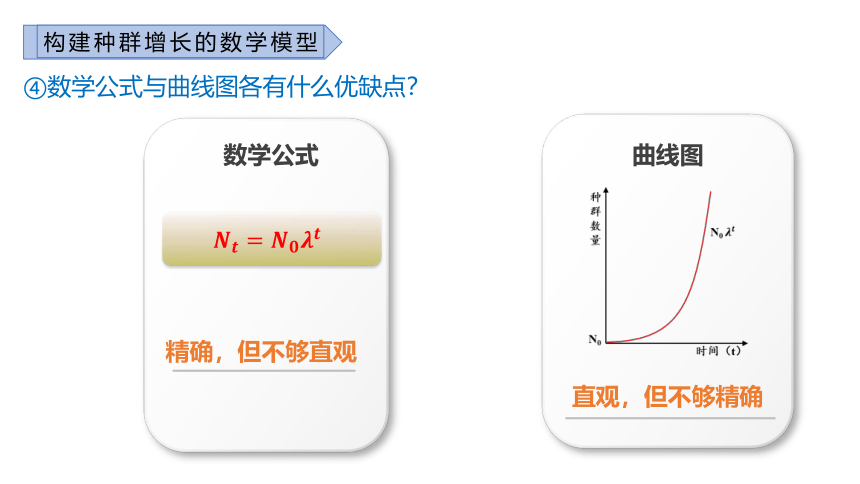
精确,但不够直观
数学公式
直观,但不够精确
曲线图
④数学公式与曲线图各有什么优缺点?
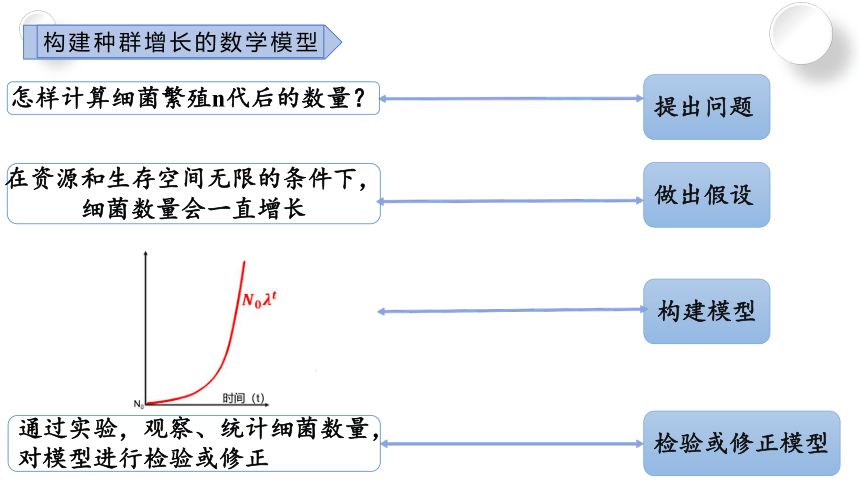
提出问题
做出假设
构建模型
检验或修正模型
怎样计算细菌繁殖n代后的数量?
在资源和生存空间无限的条件下,细菌数量会一直增长
通过实验,观察、统计细菌数量,对模型进行检验或修正
构建种群增长的数学模型
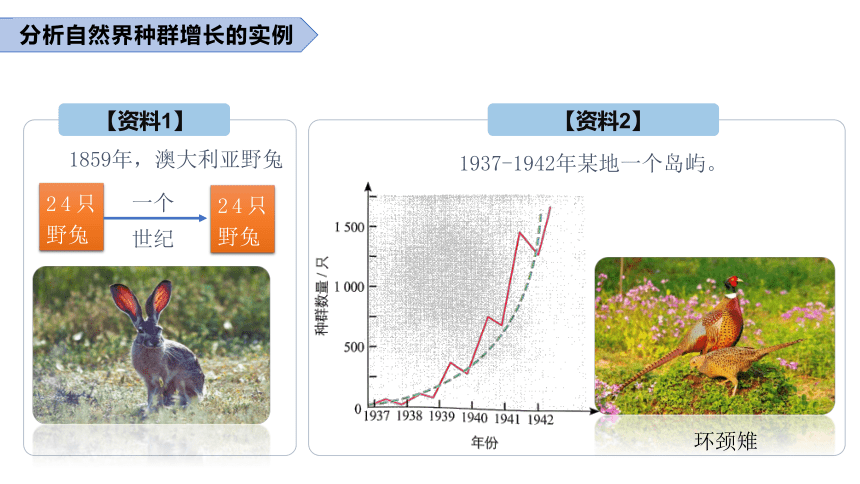
【资料1】
1859年,澳大利亚野兔
24只野兔
24只野兔
一个
世纪
1937-1942年某地一个岛屿。
【资料2】
环颈雉
分析自然界种群增长的实例
①这两个资料中的种群增长有什么共同点?
②种群出现这种增长的原因是什么?
③这种种群增长的趋势能不能一直持续下去?为什么?
这两个资料中,种群数量增长曲线都大致呈“J”形。
种群呈“J”形曲线增长的原因是食物和空间条件充裕、没有天敌、气候适宜等。
不能
理想条件
因为食物等资源和空间是有无限的。
分析自然界种群增长的实例
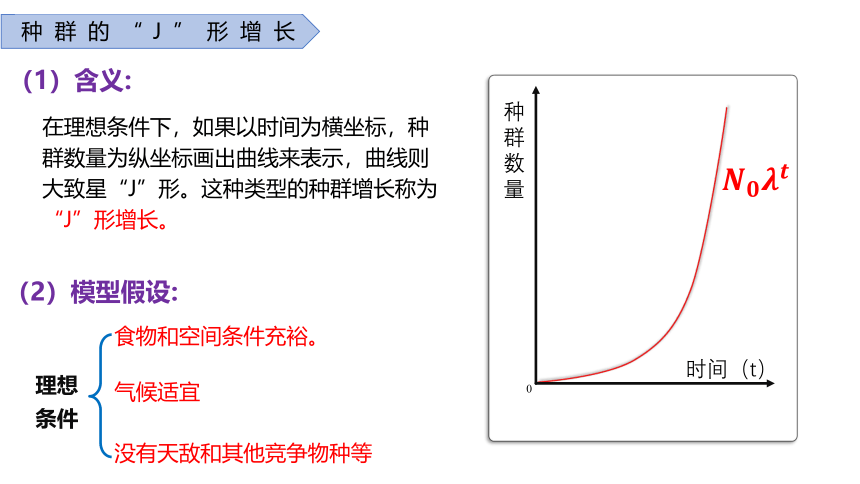
(1)含义:
在理想条件下,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致星“J”形。这种类型的种群增长称为“J”形增长。
(2)模型假设:
理想条件
食物和空间条件充裕。
气候适宜
没有天敌和其他竞争物种等
时间(t)
种群数量
0
种群的“J”形增长
(3)“J”形增长的数学模型:
N0 :为起始数量;
t:为时间;
Nt :表示t年后该种群的数量;
λ :表示该种群数量是前一年种群数量的倍数。
数学公式
t年后种群的数量为:
Nt=N0×λt
时间(t)
种群数量
0
种群的“J”形增长
①当入=1时,种群数量如何变化
②当入>1时,种群数量如何变化
③当入<1时,种群数量如何变化
④当入>1时,种群一定呈“J”形增长吗
种群数量不变(相对稳定)
种群数量增长
种群数量下降
不一定;只有入>1且为定值时,种群增长才为“J”形增长;
请据图分析,种群数量变化符合数学公式: Nt=N0×λt 时,种群增长曲线一定是“J”形吗
种群的“J”形增长
②增长速率:单位时间内增加的个体数量。
=
增长速率=
末数-初数
单位时间
Nt-Nt-1(个)
t(年)
实质就是“J”型曲线的斜率
请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率曲线模型。
时间(t)
种群数量
0
时间(t)
种群增长速率
0
Nt
种群“J”形曲线的增长速率
①增长率 =(现有个体数-原有个体数)÷种群原有个体数
=
×100%
增长率=
末数-初数
Nt-Nt-1
Nt-1
初数
λ-1
(λ>1,且不变)
请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率曲线模型。
时间(t)
种群数量
0
时间(t)
种群增长率
0
Nt
种群“J”形曲线的增长率
时间/d
种群数量/个
1 2 3 4 5 6
400
大草履虫种群的增长曲线
300
200
100
0
在0.5 mL培养液中放入5个大草履虫,每隔24 h统计一次大草履虫的数量。
种群的“S”形增长
种群的“S”形增长
1.尝试用语言描述一下这条曲线
2.大草履虫的种群增长曲线与“J”形曲线有什么不同?
时间(t)
种群数量
0
时间/d
种群数量/个
1 2 3 4 5 6
400
大草履虫种群的增长曲线
300
200
100
0
“S”形
种群的“S”形增长
种群的“S”形增长
时间/d
种群数量/个
1 2 3 4 5 6
400
大草履虫种群的增长曲线
300
200
100
0
3. 造成曲线变平缓的原因是什么?
种群密度增加
种内竞争加剧
敌害数量增加
出生率降低,死亡率升高
出生率=死亡率
停止增长
资源、空间有限
种群的“S”形增长
时间/d
种群数量/个
1 2 3 4 5 6
400
K= 375
大草履虫种群的增长曲线
300
200
100
0
4. “K“这个数值意味着什么?
一定的环境条件所能维持的种群最大数量称为环境容纳量,又称K 值。
5. 哪一个阶段种群数量增长最快??
大概K/2处
1/2K
种群的“S”形增长
=N0: ,
K/2: ,
=K/2: ,
K/2: ,
=K: ,
大草履虫种群的增长曲线
种群增长速率
t1
K
t2
1/2K
t0
增长速率:单位时间内的新增个体数
增长速率=
末数-初数
单位时间
增长速率=0
增长速率逐渐增大
增长速率最大
增长速率逐渐减小
增长速率=0
0
斜率
种群“S”形曲线的增长速率
增长率 :单位时间内新增个体数占原有个体数的比值
=
增长率=
出生数 - 死亡数
原种群个体总数
出生率 - 死亡率
种群增长率
t1
K
t2
t0
0
大草履虫种群的增长曲线
种群“S”形曲线的增长率
“J”形增长 “S”形增长
条件
增长模型
K值
食物和空间条件充裕、气候适宜、没有天敌和其他竞争物种等理想条件。
资源和空间有限、受气候变化影响、受其他生物制约。
有K值
无K值
“S”形与“J”形曲线的区别
阴影表示环境阻力,两条曲线数量差表示被淘汰的个体数。
在“S”形增长曲线的开始部分可以视为“J”形曲线吗?
不能,因为环境阻力一开始就存在
“S”形与“J”形曲线的联系
同种生物的K值是固定不变的吗?
环境遭到破坏时,K值下降
K值一定是种群数量的最大值吗?
K值并不一定是种群数量的最大值
种群数量在K值附近上下波动,若超过K值,环境被破坏。
K值会随着环境的改变而发生变化
环境条件状况改善时,K值上升
环境容纳量:一定的环境条件所能维持的种群最大数量称为环境容纳量.
环境容纳量(K值)
大熊猫数量锐减的原因是什么?
野生动物资源保护措施
栖息地遭到破坏,活动范围减小、食物减少——环境阻力变大
K值减小
建立自然保护区,减小环境阻力,提高环境容纳量(K值)
给予更宽广的生存空间,改善栖息环境
环境容纳量的应用
繁殖力强、破坏力大
2.有害生物的防治
出生率
死亡率
降低种群数量
降低环境容纳量
捕杀(老鼠夹等)、老鼠药等
增大环境阻力
在K/2前防治
环境容纳量的应用
种群数量在K值附近上下波动,若超过K值,环境被破坏。
草原最大载畜量不超过K值
合理确定载畜量
环境容纳量的应用
渔业捕捞后的种群数量要控制在?
K值
K/2值
最短时间恢复种群数量,有利于持续获得较大收获量。
种群增长速率
t1
K
t2
1/2K
t0
环境容纳量的应用
种群的数量增长
时间(min) 20 40 60 80 100 120 140 160 180
分裂次数 1 2 3 4 5 6 7 8 9
数量(个)
2
4
8
16
32
64
128
256
512
①细菌的繁殖方式是怎样的
二分裂
②请你计算一个细菌产生的后代在不同时间的数量:
构建种群增长的数学模型
③假设细菌初始数量为N0,第n代细菌数量的计算公式是什么?
Nn= N0×2n
曲线图
构建种群增长的数学模型
构建种群增长的数学模型
以 为横坐标
以 为纵坐标
时间
细菌数量
0 20 40 60 80 100 120 140
551
501
451
401
351
201
151
51
1
时间/min
细菌数量/个
构建种群增长的数学模型
精确,但不够直观
数学公式
直观,但不够精确
曲线图
④数学公式与曲线图各有什么优缺点?
提出问题
做出假设
构建模型
检验或修正模型
怎样计算细菌繁殖n代后的数量?
在资源和生存空间无限的条件下,细菌数量会一直增长
通过实验,观察、统计细菌数量,对模型进行检验或修正
构建种群增长的数学模型
【资料1】
1859年,澳大利亚野兔
24只野兔
24只野兔
一个
世纪
1937-1942年某地一个岛屿。
【资料2】
环颈雉
分析自然界种群增长的实例
①这两个资料中的种群增长有什么共同点?
②种群出现这种增长的原因是什么?
③这种种群增长的趋势能不能一直持续下去?为什么?
这两个资料中,种群数量增长曲线都大致呈“J”形。
种群呈“J”形曲线增长的原因是食物和空间条件充裕、没有天敌、气候适宜等。
不能
理想条件
因为食物等资源和空间是有无限的。
分析自然界种群增长的实例
(1)含义:
在理想条件下,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致星“J”形。这种类型的种群增长称为“J”形增长。
(2)模型假设:
理想条件
食物和空间条件充裕。
气候适宜
没有天敌和其他竞争物种等
时间(t)
种群数量
0
种群的“J”形增长
(3)“J”形增长的数学模型:
N0 :为起始数量;
t:为时间;
Nt :表示t年后该种群的数量;
λ :表示该种群数量是前一年种群数量的倍数。
数学公式
t年后种群的数量为:
Nt=N0×λt
时间(t)
种群数量
0
种群的“J”形增长
①当入=1时,种群数量如何变化
②当入>1时,种群数量如何变化
③当入<1时,种群数量如何变化
④当入>1时,种群一定呈“J”形增长吗
种群数量不变(相对稳定)
种群数量增长
种群数量下降
不一定;只有入>1且为定值时,种群增长才为“J”形增长;
请据图分析,种群数量变化符合数学公式: Nt=N0×λt 时,种群增长曲线一定是“J”形吗
种群的“J”形增长
②增长速率:单位时间内增加的个体数量。
=
增长速率=
末数-初数
单位时间
Nt-Nt-1(个)
t(年)
实质就是“J”型曲线的斜率
请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率曲线模型。
时间(t)
种群数量
0
时间(t)
种群增长速率
0
Nt
种群“J”形曲线的增长速率
①增长率 =(现有个体数-原有个体数)÷种群原有个体数
=
×100%
增长率=
末数-初数
Nt-Nt-1
Nt-1
初数
λ-1
(λ>1,且不变)
请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率曲线模型。
时间(t)
种群数量
0
时间(t)
种群增长率
0
Nt
种群“J”形曲线的增长率
时间/d
种群数量/个
1 2 3 4 5 6
400
大草履虫种群的增长曲线
300
200
100
0
在0.5 mL培养液中放入5个大草履虫,每隔24 h统计一次大草履虫的数量。
种群的“S”形增长
种群的“S”形增长
1.尝试用语言描述一下这条曲线
2.大草履虫的种群增长曲线与“J”形曲线有什么不同?
时间(t)
种群数量
0
时间/d
种群数量/个
1 2 3 4 5 6
400
大草履虫种群的增长曲线
300
200
100
0
“S”形
种群的“S”形增长
种群的“S”形增长
时间/d
种群数量/个
1 2 3 4 5 6
400
大草履虫种群的增长曲线
300
200
100
0
3. 造成曲线变平缓的原因是什么?
种群密度增加
种内竞争加剧
敌害数量增加
出生率降低,死亡率升高
出生率=死亡率
停止增长
资源、空间有限
种群的“S”形增长
时间/d
种群数量/个
1 2 3 4 5 6
400
K= 375
大草履虫种群的增长曲线
300
200
100
0
4. “K“这个数值意味着什么?
一定的环境条件所能维持的种群最大数量称为环境容纳量,又称K 值。
5. 哪一个阶段种群数量增长最快??
大概K/2处
1/2K
种群的“S”形增长
=N0: ,
K/2: ,
=K/2: ,
K/2: ,
=K: ,
大草履虫种群的增长曲线
种群增长速率
t1
K
t2
1/2K
t0
增长速率:单位时间内的新增个体数
增长速率=
末数-初数
单位时间
增长速率=0
增长速率逐渐增大
增长速率最大
增长速率逐渐减小
增长速率=0
0
斜率
种群“S”形曲线的增长速率
增长率 :单位时间内新增个体数占原有个体数的比值
=
增长率=
出生数 - 死亡数
原种群个体总数
出生率 - 死亡率
种群增长率
t1
K
t2
t0
0
大草履虫种群的增长曲线
种群“S”形曲线的增长率
“J”形增长 “S”形增长
条件
增长模型
K值
食物和空间条件充裕、气候适宜、没有天敌和其他竞争物种等理想条件。
资源和空间有限、受气候变化影响、受其他生物制约。
有K值
无K值
“S”形与“J”形曲线的区别
阴影表示环境阻力,两条曲线数量差表示被淘汰的个体数。
在“S”形增长曲线的开始部分可以视为“J”形曲线吗?
不能,因为环境阻力一开始就存在
“S”形与“J”形曲线的联系
同种生物的K值是固定不变的吗?
环境遭到破坏时,K值下降
K值一定是种群数量的最大值吗?
K值并不一定是种群数量的最大值
种群数量在K值附近上下波动,若超过K值,环境被破坏。
K值会随着环境的改变而发生变化
环境条件状况改善时,K值上升
环境容纳量:一定的环境条件所能维持的种群最大数量称为环境容纳量.
环境容纳量(K值)
大熊猫数量锐减的原因是什么?
野生动物资源保护措施
栖息地遭到破坏,活动范围减小、食物减少——环境阻力变大
K值减小
建立自然保护区,减小环境阻力,提高环境容纳量(K值)
给予更宽广的生存空间,改善栖息环境
环境容纳量的应用
繁殖力强、破坏力大
2.有害生物的防治
出生率
死亡率
降低种群数量
降低环境容纳量
捕杀(老鼠夹等)、老鼠药等
增大环境阻力
在K/2前防治
环境容纳量的应用
种群数量在K值附近上下波动,若超过K值,环境被破坏。
草原最大载畜量不超过K值
合理确定载畜量
环境容纳量的应用
渔业捕捞后的种群数量要控制在?
K值
K/2值
最短时间恢复种群数量,有利于持续获得较大收获量。
种群增长速率
t1
K
t2
1/2K
t0
环境容纳量的应用
