平面与平面的位置关系[上学期]
图片预览



文档简介
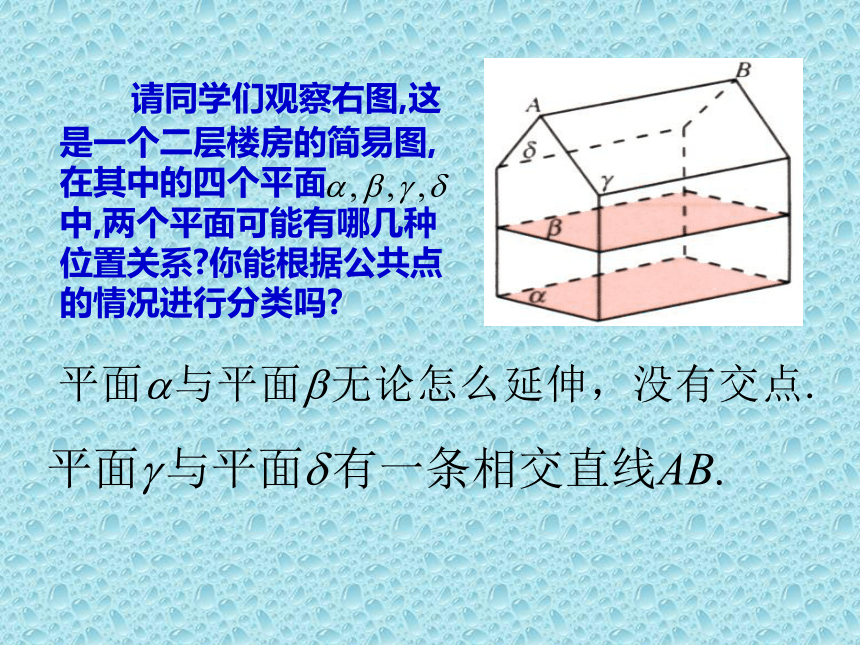
课件18张PPT。平面与平面的位置关系深大附中 请同学们观察右图,这是一个二层楼房的简易图,在其中的四个平面
中,两个平面可能有哪几种位置关系?你能根据公共点的情况进行分类吗? 如果两个平面没有公共点,我们就
说这两个平面互相平行. 如果两个平面有一个公共点,由公
理2可知,那么它们相交于经过这个点
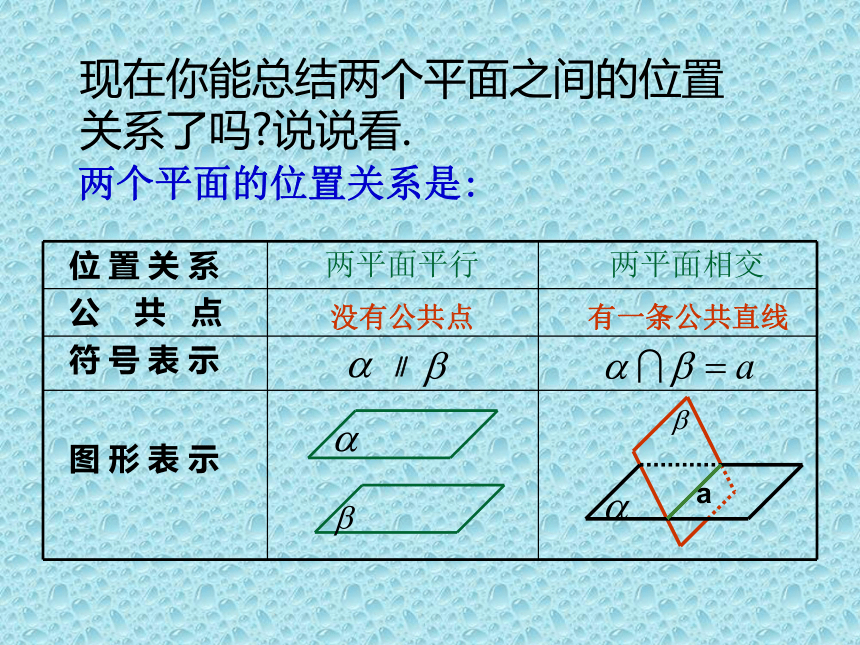
的一条直线.面面平行的定义:现在你能总结两个平面之间的位置
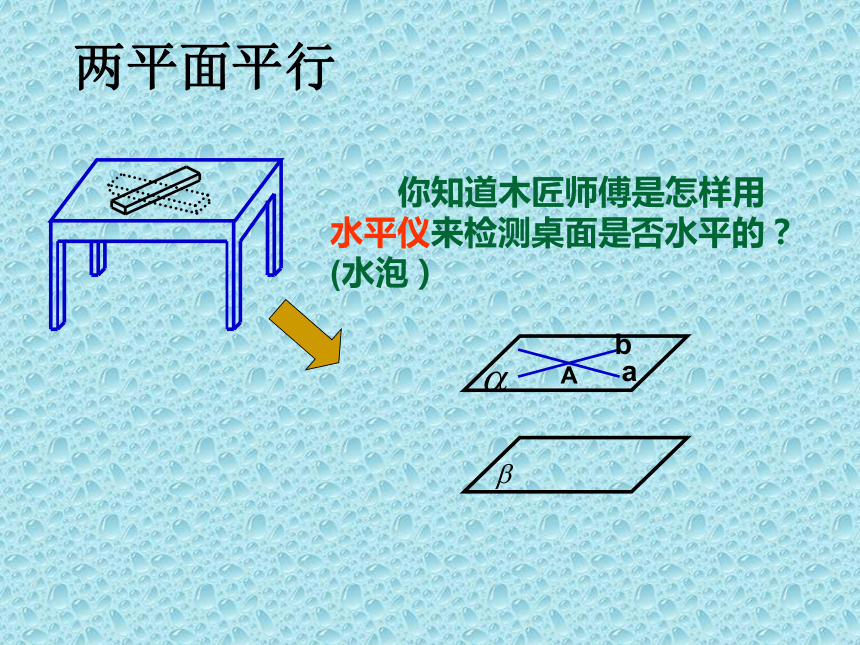
关系了吗?说说看.两个平面的位置关系是:没有公共点有一条公共直线∥两平面平行 你知道木匠师傅是怎样用
水平仪来检测桌面是否水平的?
(水泡)探究思考:(两平面平行) (两平面相交) (两平面平行) (两平面相交) 两个平面平行的判定定理: 如果一个平面内有两条相交直线都平行
于另一个平面,那么这两个平面平行.符号语言:且 a∥ , b∥ ,则 ∥ 图形语言:例1.如图,在长方体ABCD-A1B1C1D1中,
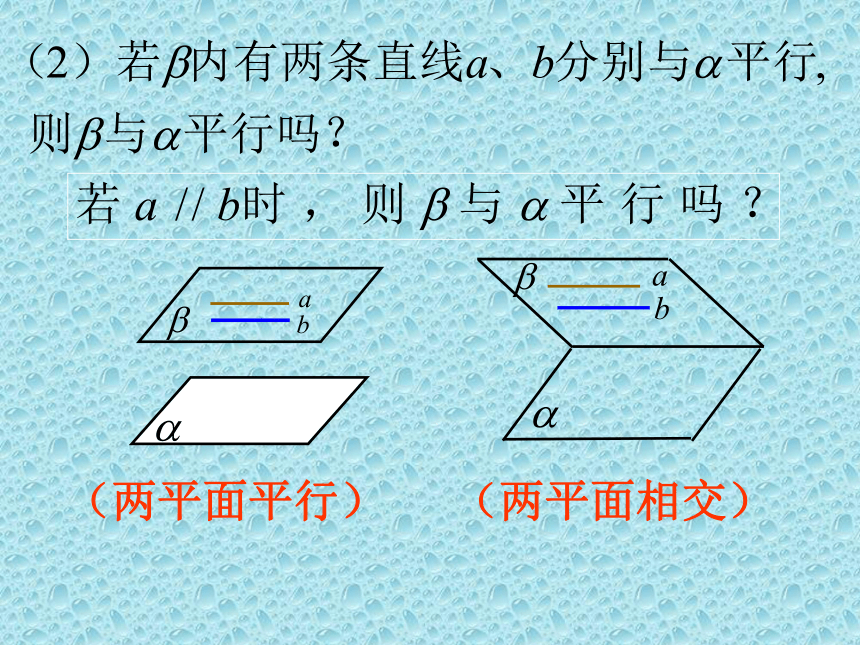
求证:平面C1DB∥平面AB1D1.分析:只要证到一个平面内有两条相交直线和另一个平面平行即可.例题讲解:如果两个平面平行,那么:(1)一个平面内的直线是否平行于另一个平面? (2)分别在两个平面内的两条直线是否平行? 对于第一个问题根据线面平行和面面平行的概
念可知正确.第二个问题有两中可能:分别是平行或异面.合作探究:两个平面平行的性质定理: 如果两个平行平面同时和第三个平面相交,
那么它们的交线平行.已知: ∥
求证: ∥证明:因为 ∥ ,
所以 与 没有公共点,
因而交线 , 也没有公共点,
又因为 , 都在平面 内,
所以 ∥ 例2.求证:如果一条直线垂直于两个平行平
面中的一个平面,那么它也垂直于另一个平面.已知: ∥ , ,
求证: .分析:要证 ,只要证明 垂直
于平面 内的任意一条直线或某两
条相交直线.数学应用:思考:如何做辅助线?面面平行中有关的概念: 与两个平行平面都垂直的直线,叫做这两个平行平面的公垂线. 它夹在这两个平行平面间的线段,叫做这两个平行平面的公垂线段.根据两个平面平行的性质定理,有AA′∥BB′.所以四边形ABB′A′是平行四边形,
故AA′=BB′. 结论:由两个平行平面的公垂线都相等,我们
把公垂线的长度叫做两个平行平面间的距离.1.判断下列命题是否正确,并说明理由.(3).平行于同一条直线的两个平面平行. ( )(4).过已知平面外一点,有且只有一个平面与已知平面平行. ( )(5).过已知平面外一条直线,必能作出与已知平面平行的平面. ( )(2).若平面 内有无数条直线与平面 平行,则 与 平行. ( )(1).若平面 内的两条直线分别与平面 平行,则 与 平行. ( ) 2.六棱柱的表面中,互相平行的面最多
有_________对.××××√4巩固练习: 3.如图,设E,F,E1,F1分别是长方体
ABCD-A1B1C1D1的棱AB,CD,A1B1,
C1D1的中点.
求证:平面ED1∥平面BF1.分析:在其中一个平面内找两条
相交直线平行另一个平面即可.4.求证:夹在两个平行平面间的平行线段相等.已知: ∥ ,AA′∥ BB′,
A∈ ,A ∈ ,B ∈ ,B′∈ ,
求证: AA′= BB′. 课堂小结1.空间两个平面的位置关系.2.两个平行平面的判定定理.3.两个平行平面的性质定理. 4.两个平行平面的公垂线的概念,
公垂线段的概念以及两个平行
平面的距离.谢谢观赏!
中,两个平面可能有哪几种位置关系?你能根据公共点的情况进行分类吗? 如果两个平面没有公共点,我们就
说这两个平面互相平行. 如果两个平面有一个公共点,由公
理2可知,那么它们相交于经过这个点
的一条直线.面面平行的定义:现在你能总结两个平面之间的位置
关系了吗?说说看.两个平面的位置关系是:没有公共点有一条公共直线∥两平面平行 你知道木匠师傅是怎样用
水平仪来检测桌面是否水平的?
(水泡)探究思考:(两平面平行) (两平面相交) (两平面平行) (两平面相交) 两个平面平行的判定定理: 如果一个平面内有两条相交直线都平行
于另一个平面,那么这两个平面平行.符号语言:且 a∥ , b∥ ,则 ∥ 图形语言:例1.如图,在长方体ABCD-A1B1C1D1中,
求证:平面C1DB∥平面AB1D1.分析:只要证到一个平面内有两条相交直线和另一个平面平行即可.例题讲解:如果两个平面平行,那么:(1)一个平面内的直线是否平行于另一个平面? (2)分别在两个平面内的两条直线是否平行? 对于第一个问题根据线面平行和面面平行的概
念可知正确.第二个问题有两中可能:分别是平行或异面.合作探究:两个平面平行的性质定理: 如果两个平行平面同时和第三个平面相交,
那么它们的交线平行.已知: ∥
求证: ∥证明:因为 ∥ ,
所以 与 没有公共点,
因而交线 , 也没有公共点,
又因为 , 都在平面 内,
所以 ∥ 例2.求证:如果一条直线垂直于两个平行平
面中的一个平面,那么它也垂直于另一个平面.已知: ∥ , ,
求证: .分析:要证 ,只要证明 垂直
于平面 内的任意一条直线或某两
条相交直线.数学应用:思考:如何做辅助线?面面平行中有关的概念: 与两个平行平面都垂直的直线,叫做这两个平行平面的公垂线. 它夹在这两个平行平面间的线段,叫做这两个平行平面的公垂线段.根据两个平面平行的性质定理,有AA′∥BB′.所以四边形ABB′A′是平行四边形,
故AA′=BB′. 结论:由两个平行平面的公垂线都相等,我们
把公垂线的长度叫做两个平行平面间的距离.1.判断下列命题是否正确,并说明理由.(3).平行于同一条直线的两个平面平行. ( )(4).过已知平面外一点,有且只有一个平面与已知平面平行. ( )(5).过已知平面外一条直线,必能作出与已知平面平行的平面. ( )(2).若平面 内有无数条直线与平面 平行,则 与 平行. ( )(1).若平面 内的两条直线分别与平面 平行,则 与 平行. ( ) 2.六棱柱的表面中,互相平行的面最多
有_________对.××××√4巩固练习: 3.如图,设E,F,E1,F1分别是长方体
ABCD-A1B1C1D1的棱AB,CD,A1B1,
C1D1的中点.
求证:平面ED1∥平面BF1.分析:在其中一个平面内找两条
相交直线平行另一个平面即可.4.求证:夹在两个平行平面间的平行线段相等.已知: ∥ ,AA′∥ BB′,
A∈ ,A ∈ ,B ∈ ,B′∈ ,
求证: AA′= BB′. 课堂小结1.空间两个平面的位置关系.2.两个平行平面的判定定理.3.两个平行平面的性质定理. 4.两个平行平面的公垂线的概念,
公垂线段的概念以及两个平行
平面的距离.谢谢观赏!
