河南省安阳市名校2022-2023学年高一下学期6月阶段测试数学试题(含答案)
文档属性
| 名称 | 河南省安阳市名校2022-2023学年高一下学期6月阶段测试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 784.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-18 00:00:00 | ||
图片预览



文档简介
安阳市名校2022-2023学年高一下学期6月阶段测试
数学试题
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设向量,,且,则向量与b的夹角为( )
A. B. C. D.
2.已知复数为纯虚数(其中i为虚数单位),则实数( )
A.-3 B.3 C. D.
3.用斜二测画法画水平放置的的直观图,得到如图所示的等腰直角三角形.已知点O'是斜边B'C'的中点,且,则中BC边上的高为( )
A.1 B.2 C. D.
4.在三棱柱中,平面ABC,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
5.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番。为更好地了解该地区农村的经济收入变化情况,统计了该地区系农村建设前后农村的经济收入构成比例。得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
6.为了了解某校九年级1600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.根据统计图的数据,下列结论错误的是( )
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约为320
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约为32
7.某班学生在一次数学考试中的成绩分布如表:
分数段
人数 2 5 6 8 12 6 4 2
那么分数在中的频率约是(精确到0.01)( )
A.0.18 B.0.47 C.0.50 D.0.38
8.《史记》中讲述了田忌与齐王赛马的故事:“田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.”若双方各自拥有上等马、中等马、下等马各1匹,从中随机选1匹进行1场比赛,则齐王的马获胜的概率为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.在中,角A,B,C所对的边分别为a,b,c,若,,,则下列结论正确的是( )
A. B.
C. D.中的面积为
10.如图,正方体的棱长为1,线段上有两个动点E,F,且,则下列结论正确的是( )
A.
B.平面ABCD
C.的面积与的面积相等
D.三棱锥的体积为定值
11.某学校为了调查学生一周在生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在内的学生有60人,则下列说法正确的是( )
A.样本中支出在内的频率为0.03
B.样本中支出不少于40元的人数为132
C.n的值为200
D.若该校有2000名学生,则定有600人支出在内
12.甲罐中有3个红球、2个白球,乙罐中有4个红球、1个白球,先从甲罐中随机取出1个球放入乙罐,分别以,表示从甲罐中取出的球是红球、白球的事件,再从乙罐中随机取出1个球,以B表示从乙罐中取出的球是红球的事件,下列说法正确的是( )
A. B. 事件B与事件相互独立
C.事件B与事件相互独立 D.,互斥
三、填空题:本题共4小题,每小题5分,共20分。
13.若复数z满足(i为虚数单位),则______.
14.已知四棱锥的底面ABCD是边长为a的正方形,且平面ABCD,,点M为线段PC上的动点(不包含端点),则当三棱锥的外接球的表面积最小时,CM的长为__________.
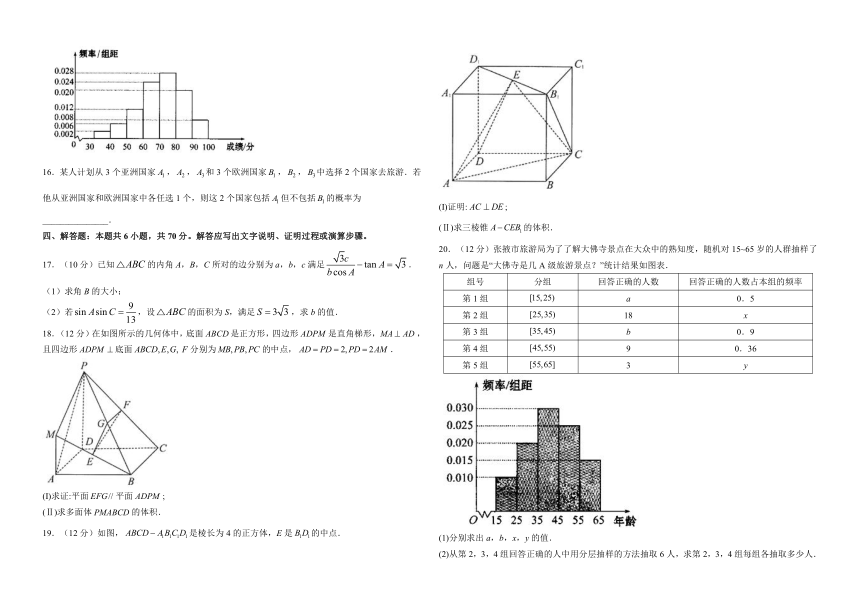
15.某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是_________.
16.某人计划从3个亚洲国家,,和3个欧洲国家,,中选择2个国家去旅游.若他从亚洲国家和欧洲国家中各任选1个,则这2个国家包括但不包括的概率为_______________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)已知的内角A,B,C所对的边分别为a,b,c满足.
(1)求角B的大小;
(2)若,设的面积为S,满足,求b的值.
18.(12分)在如图所示的几何体中,底面是正方形,四边形是直角梯形,,且四边形底面分别为的中点,.
(I)求证:平面平面;
(Ⅱ)求多面体的体积.
19.(12分)如图,是棱长为4的正方体,E是的中点.
(I)证明:;
(Ⅱ)求三棱锥的体积.
20.(12分)张掖市旅游局为了了解大佛寺景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,问题是“大佛寺是几A级旅游景点?”统计结果如图表.
组号 分组 回答正确的人数 回答正确的人数占本组的频率
第1组 a 0.5
第2组 18 x
第3组 b 0.9
第4组 9 0.36
第5组 3 y
(1)分别求出a,b,x,y的值.
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人.
21.(12分)某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,并整理得到如下频率分布直方图.
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率.
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间内的人数.
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
22.(12分)某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表如图,其中“√”表示购买,“×”表示未购买.
甲 乙 丙 丁
100 √ × √ √
217 × √ × √
200 √ √ √ ×
300 √ × √ ×
85 √ × × ×
98 × √ × ×
(1)估计顾客同时购买乙和丙的概率.
(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率.
(3)如果顾客购买了甲,那么该顾客同时购买乙、丙、丁中那种商品的可能性最大?
答案以及解析
1.答案:D
解析:由,,,得,解得,则,设向量与b的夹角为,,则,.故选D.
2.答案:A
解析:,
因为z为纯虚数,则,解得.故选A.
3.答案:D
解析:直观图是等腰直角三角形,,,.根据直观图中平行于y轴的长度变为原来的一半,的BC边上的高.故选D.
4.答案:D
解析:平面ABC,,又,,又,,平面,该三棱柱可以补形成长方体,连接,,则,是与所成的角或其补角.令,则,在中,,,由余弦定理得.故选D.
5.答案:A
解析:设建设前总经济收入为100则建设后总经济收入为200
对于A,建设前种植收入为,建设后种植收入为故A借误:
对于B,建设前其他收入为,建设后其他收入为,故B正确
对于C,建设前养殖收入为,建设后养殖收入为,故C正确:
对于D,建设后,养殖收入占,第三产业收入占故D正确:
6.答案:D
解析:由题图可知,该校九年级学生1分钟仰卧起坐的次数的中位数是次,众数是27.5次,1分钟仰卧起坐的次数超过30次的频率为0.2,所以该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人,故A,B,C正确;1分钟仰卧起坐的次数少于20次的频率为0.1,所以该校九年级学生1分钟仰卧起坐的次数少于20次的约有160人,故D错误.
7.答案:A
解析:班级总人数为,成绩在中的有8人,其频率为.
8.答案:A
解析:记田忌的上等马、中等马、下等马分别为a,b,c,齐王的上等马、中等马、下等马分别为A,B,C.由题意可知,所有的基本事件有aA,bA,cA,aB,bB,cB,aC,bC,cC,共9种,其中田忌可以获胜的事件有aB,aC,bC,共3种,则齐王的马获胜的概率.故选A.
9.答案:BC
解析:由,得.由,得,.若,则,与矛盾,故,A错误,则,由,,得,,所以,所以,故,B正确.由正弦定理,得,C正确,所以的面积为,D错误.
10.答案:ABD
解析:A项,为正方体平面,故A项正确;
B项,显然,即,所以平面ABCD,故B项正确;
C项,易证是边长为的正三角形,故点A到的距离,而点B到的距离,所以,,故C项错误;
D项,显然点A到平面BEF的距离,所以为定值,故D项正确.
11.答案:BC
解析:样本中支出在内的频率为,故A错误;样本中支出不少于40元的人数为,故B正确;,故n的值为200,故C正确;若该校有2000名学生,则可能有人支出在内,故D错误.故选BC.
12.答案:AD
解析:根据题意画出树状图,得到有关事件的样本点数:
因此,,,故A正确;
又,,故B错误;同理,C错误;
显然,不可能同时发生,故,互斥,故D正确.故选AD.
13.答案:
解析:由,
得,
所以,则,
所以.
故答案为:.
14.答案:
解析:连接MA,由题意可知三棱锥的外接球即四棱锥的外接球,则当三棱锥外接球的表面积最小时,四棱锥外接球的半径最小.设四棱锥外接球的球心为O,半径为R,连接AC与BD交于点.当O与不重合时,连接,易知平面ABCD,则,
连接OC,在中,.当O与重合时,,所以当三棱锥的外接球的表面积最小时,O与重合,.设CM的中点为N,连接,易知,则,
所以,解得,所以.
15.答案:600
解析:由题意知,在该次数学考试中成绩小于60分的频率为,故这3000名学生在该次数学考试中成绩小于60分的学生数是.
16.答案:
解析:从3个非洲国家和3个欧洲国家中各任选1个,所有样本点为,,,,,,,,,共9种.其中包括但不包括的事件所包含的样本点有,,共2种,所以所求事件的概率.
17、(1)答案:
解析:由,得,
根据正弦定理,得.
因为,
所以,
所以.
因为,所以,所以,则.
(2)答案:
解析:由,得.
又由正弦定理得,
所以,解得.
18.答案:(I)见解析
(Ⅱ)
解析:(I)证明:分别为的中点,
.
又∵四边形是正方形,
,
.
平面平面,
平面平面.
又平面,
∴平面平面.
(Ⅱ)∵四边形是直角梯形,,
.
又∵四边形底面,平面平面平面,
平面,
是四棱锥的高,
.
∵四边形是正方形,
.
平面平面,
.
又平面.
平面,即是三棱锥的高,
,
∴多面体的体积.
19.答案:(I)见解析
(Ⅱ)
解析:(I)证明:连接.
∵四边形是正方形,
.
在正方体中,
平面,
又平面,
.
又平面,平面,
平面.
又平面,
.
(Ⅱ)设与交于点F,连接.
在正方体中,.
又分别是的中点,
,
∴四边形是平行四边形,
.
过平面平面,
平面.
又正方体的棱长为4,
.
20.答案:(1).
(2)第2组2人,第3组3人,第4组1人.
解析:(1)由频率分布表中第4组数据可知,第4组总人数为,
结合频率分布直方图可知.
所以.
,.
(2)因为第2,3,4组回答正确的共有54人,所以利用分层随机抽样在54人中抽取6人,每组分别抽取的人数为第2组:;第3组:;第4组:.
21.答案:(1)概率估计为0.4
(2)估计为20
(3)比例为
解析:(1)根据频率分布直方图可知,样本中分数不小于70的频率为,
所以样本中分数小于70的频率为,所以从总体的400名学生中随机抽取一人,其分数小于70的概率估计为0.4.
(2)根据题意,样本中分数不小于50的频率为,
分数在区间内的人数为,
所以总体中分数在区间内的人数估计为.
(3)由题意可知,样本中分数不小于70的学生人数为,
所以样本中分数不小于70的男生人数为,
所以样本中的男生人数为,女生人数为,
所以样本中男生和女生人数的比例为,所以根据分层抽样原理,估计总体中男生和女生人数的比例为.
22.答案:(1)同时购买乙和丙的概率为0.2
(2)同时购买3种商品的概率估计为0.3
(3)同时购买丙的可能性最大
解析:(1)从统计表可以看出,在这1000位顾客中有200位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为.
(2)从统计表可以看出,在这1000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品.
所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为.
(3)与(1)同理,可得顾客同时购买甲和乙的概率可以估计为,
顾客同时购买甲和丙的概率可以估计为,
1000顾客同时购买甲和丁的概率可以估计为.
所以如果顾客购买了甲,那么该顾客同时购买丙的可能性最大.
数学试题
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设向量,,且,则向量与b的夹角为( )
A. B. C. D.
2.已知复数为纯虚数(其中i为虚数单位),则实数( )
A.-3 B.3 C. D.
3.用斜二测画法画水平放置的的直观图,得到如图所示的等腰直角三角形.已知点O'是斜边B'C'的中点,且,则中BC边上的高为( )
A.1 B.2 C. D.
4.在三棱柱中,平面ABC,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
5.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番。为更好地了解该地区农村的经济收入变化情况,统计了该地区系农村建设前后农村的经济收入构成比例。得到如下饼图:
则下面结论中不正确的是( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
6.为了了解某校九年级1600名学生的体能情况,随机抽查了部分学生,测试1分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.根据统计图的数据,下列结论错误的是( )
A.该校九年级学生1分钟仰卧起坐的次数的中位数为26.25次
B.该校九年级学生1分钟仰卧起坐的次数的众数为27.5次
C.该校九年级学生1分钟仰卧起坐的次数超过30次的人数约为320
D.该校九年级学生1分钟仰卧起坐的次数少于20次的人数约为32
7.某班学生在一次数学考试中的成绩分布如表:
分数段
人数 2 5 6 8 12 6 4 2
那么分数在中的频率约是(精确到0.01)( )
A.0.18 B.0.47 C.0.50 D.0.38
8.《史记》中讲述了田忌与齐王赛马的故事:“田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.”若双方各自拥有上等马、中等马、下等马各1匹,从中随机选1匹进行1场比赛,则齐王的马获胜的概率为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.在中,角A,B,C所对的边分别为a,b,c,若,,,则下列结论正确的是( )
A. B.
C. D.中的面积为
10.如图,正方体的棱长为1,线段上有两个动点E,F,且,则下列结论正确的是( )
A.
B.平面ABCD
C.的面积与的面积相等
D.三棱锥的体积为定值
11.某学校为了调查学生一周在生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在内的学生有60人,则下列说法正确的是( )
A.样本中支出在内的频率为0.03
B.样本中支出不少于40元的人数为132
C.n的值为200
D.若该校有2000名学生,则定有600人支出在内
12.甲罐中有3个红球、2个白球,乙罐中有4个红球、1个白球,先从甲罐中随机取出1个球放入乙罐,分别以,表示从甲罐中取出的球是红球、白球的事件,再从乙罐中随机取出1个球,以B表示从乙罐中取出的球是红球的事件,下列说法正确的是( )
A. B. 事件B与事件相互独立
C.事件B与事件相互独立 D.,互斥
三、填空题:本题共4小题,每小题5分,共20分。
13.若复数z满足(i为虚数单位),则______.
14.已知四棱锥的底面ABCD是边长为a的正方形,且平面ABCD,,点M为线段PC上的动点(不包含端点),则当三棱锥的外接球的表面积最小时,CM的长为__________.
15.某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是_________.
16.某人计划从3个亚洲国家,,和3个欧洲国家,,中选择2个国家去旅游.若他从亚洲国家和欧洲国家中各任选1个,则这2个国家包括但不包括的概率为_______________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)已知的内角A,B,C所对的边分别为a,b,c满足.
(1)求角B的大小;
(2)若,设的面积为S,满足,求b的值.
18.(12分)在如图所示的几何体中,底面是正方形,四边形是直角梯形,,且四边形底面分别为的中点,.
(I)求证:平面平面;
(Ⅱ)求多面体的体积.
19.(12分)如图,是棱长为4的正方体,E是的中点.
(I)证明:;
(Ⅱ)求三棱锥的体积.
20.(12分)张掖市旅游局为了了解大佛寺景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,问题是“大佛寺是几A级旅游景点?”统计结果如图表.
组号 分组 回答正确的人数 回答正确的人数占本组的频率
第1组 a 0.5
第2组 18 x
第3组 b 0.9
第4组 9 0.36
第5组 3 y
(1)分别求出a,b,x,y的值.
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人.
21.(12分)某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,并整理得到如下频率分布直方图.
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率.
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间内的人数.
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
22.(12分)某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成统计表如图,其中“√”表示购买,“×”表示未购买.
甲 乙 丙 丁
100 √ × √ √
217 × √ × √
200 √ √ √ ×
300 √ × √ ×
85 √ × × ×
98 × √ × ×
(1)估计顾客同时购买乙和丙的概率.
(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率.
(3)如果顾客购买了甲,那么该顾客同时购买乙、丙、丁中那种商品的可能性最大?
答案以及解析
1.答案:D
解析:由,,,得,解得,则,设向量与b的夹角为,,则,.故选D.
2.答案:A
解析:,
因为z为纯虚数,则,解得.故选A.
3.答案:D
解析:直观图是等腰直角三角形,,,.根据直观图中平行于y轴的长度变为原来的一半,的BC边上的高.故选D.
4.答案:D
解析:平面ABC,,又,,又,,平面,该三棱柱可以补形成长方体,连接,,则,是与所成的角或其补角.令,则,在中,,,由余弦定理得.故选D.
5.答案:A
解析:设建设前总经济收入为100则建设后总经济收入为200
对于A,建设前种植收入为,建设后种植收入为故A借误:
对于B,建设前其他收入为,建设后其他收入为,故B正确
对于C,建设前养殖收入为,建设后养殖收入为,故C正确:
对于D,建设后,养殖收入占,第三产业收入占故D正确:
6.答案:D
解析:由题图可知,该校九年级学生1分钟仰卧起坐的次数的中位数是次,众数是27.5次,1分钟仰卧起坐的次数超过30次的频率为0.2,所以该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人,故A,B,C正确;1分钟仰卧起坐的次数少于20次的频率为0.1,所以该校九年级学生1分钟仰卧起坐的次数少于20次的约有160人,故D错误.
7.答案:A
解析:班级总人数为,成绩在中的有8人,其频率为.
8.答案:A
解析:记田忌的上等马、中等马、下等马分别为a,b,c,齐王的上等马、中等马、下等马分别为A,B,C.由题意可知,所有的基本事件有aA,bA,cA,aB,bB,cB,aC,bC,cC,共9种,其中田忌可以获胜的事件有aB,aC,bC,共3种,则齐王的马获胜的概率.故选A.
9.答案:BC
解析:由,得.由,得,.若,则,与矛盾,故,A错误,则,由,,得,,所以,所以,故,B正确.由正弦定理,得,C正确,所以的面积为,D错误.
10.答案:ABD
解析:A项,为正方体平面,故A项正确;
B项,显然,即,所以平面ABCD,故B项正确;
C项,易证是边长为的正三角形,故点A到的距离,而点B到的距离,所以,,故C项错误;
D项,显然点A到平面BEF的距离,所以为定值,故D项正确.
11.答案:BC
解析:样本中支出在内的频率为,故A错误;样本中支出不少于40元的人数为,故B正确;,故n的值为200,故C正确;若该校有2000名学生,则可能有人支出在内,故D错误.故选BC.
12.答案:AD
解析:根据题意画出树状图,得到有关事件的样本点数:
因此,,,故A正确;
又,,故B错误;同理,C错误;
显然,不可能同时发生,故,互斥,故D正确.故选AD.
13.答案:
解析:由,
得,
所以,则,
所以.
故答案为:.
14.答案:
解析:连接MA,由题意可知三棱锥的外接球即四棱锥的外接球,则当三棱锥外接球的表面积最小时,四棱锥外接球的半径最小.设四棱锥外接球的球心为O,半径为R,连接AC与BD交于点.当O与不重合时,连接,易知平面ABCD,则,
连接OC,在中,.当O与重合时,,所以当三棱锥的外接球的表面积最小时,O与重合,.设CM的中点为N,连接,易知,则,
所以,解得,所以.
15.答案:600
解析:由题意知,在该次数学考试中成绩小于60分的频率为,故这3000名学生在该次数学考试中成绩小于60分的学生数是.
16.答案:
解析:从3个非洲国家和3个欧洲国家中各任选1个,所有样本点为,,,,,,,,,共9种.其中包括但不包括的事件所包含的样本点有,,共2种,所以所求事件的概率.
17、(1)答案:
解析:由,得,
根据正弦定理,得.
因为,
所以,
所以.
因为,所以,所以,则.
(2)答案:
解析:由,得.
又由正弦定理得,
所以,解得.
18.答案:(I)见解析
(Ⅱ)
解析:(I)证明:分别为的中点,
.
又∵四边形是正方形,
,
.
平面平面,
平面平面.
又平面,
∴平面平面.
(Ⅱ)∵四边形是直角梯形,,
.
又∵四边形底面,平面平面平面,
平面,
是四棱锥的高,
.
∵四边形是正方形,
.
平面平面,
.
又平面.
平面,即是三棱锥的高,
,
∴多面体的体积.
19.答案:(I)见解析
(Ⅱ)
解析:(I)证明:连接.
∵四边形是正方形,
.
在正方体中,
平面,
又平面,
.
又平面,平面,
平面.
又平面,
.
(Ⅱ)设与交于点F,连接.
在正方体中,.
又分别是的中点,
,
∴四边形是平行四边形,
.
过平面平面,
平面.
又正方体的棱长为4,
.
20.答案:(1).
(2)第2组2人,第3组3人,第4组1人.
解析:(1)由频率分布表中第4组数据可知,第4组总人数为,
结合频率分布直方图可知.
所以.
,.
(2)因为第2,3,4组回答正确的共有54人,所以利用分层随机抽样在54人中抽取6人,每组分别抽取的人数为第2组:;第3组:;第4组:.
21.答案:(1)概率估计为0.4
(2)估计为20
(3)比例为
解析:(1)根据频率分布直方图可知,样本中分数不小于70的频率为,
所以样本中分数小于70的频率为,所以从总体的400名学生中随机抽取一人,其分数小于70的概率估计为0.4.
(2)根据题意,样本中分数不小于50的频率为,
分数在区间内的人数为,
所以总体中分数在区间内的人数估计为.
(3)由题意可知,样本中分数不小于70的学生人数为,
所以样本中分数不小于70的男生人数为,
所以样本中的男生人数为,女生人数为,
所以样本中男生和女生人数的比例为,所以根据分层抽样原理,估计总体中男生和女生人数的比例为.
22.答案:(1)同时购买乙和丙的概率为0.2
(2)同时购买3种商品的概率估计为0.3
(3)同时购买丙的可能性最大
解析:(1)从统计表可以看出,在这1000位顾客中有200位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为.
(2)从统计表可以看出,在这1000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品.
所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为.
(3)与(1)同理,可得顾客同时购买甲和乙的概率可以估计为,
顾客同时购买甲和丙的概率可以估计为,
1000顾客同时购买甲和丁的概率可以估计为.
所以如果顾客购买了甲,那么该顾客同时购买丙的可能性最大.
同课章节目录
