类比推理[下学期]
图片预览









文档简介
课件32张PPT。类比推理(1)归纳推理的前提是几个已知的特殊现象,
归纳所得的结论是尚属未知的一般现象,
该结论超越了前提所包容的范围。(2)归纳推理得到结论的真实性需要经过证明
或实践检验。(3)归纳推理是一种具有创造性的推理。通过
归纳法得到的猜想,可以作为进一步研究
的起点,它帮助人们发现问题和提出问题。复习归纳推理的特点: 传说鲁班一次去林中伐木时被一株齿形的茅草划破了手。
是什么东西这么锋利?
他认真研究了该茅草的结构特点,原来草的边沿带有细且密的小齿,联想到自己的伐木工作,他喜出望外,何不制造一种带齿的工具来伐木?
这桩倒霉事使他发明了锯子。这个推理过程是归纳推理吗?二、类比推理的定义 两类对象具有某些类似特征,由其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.
类比推理是由特殊到特殊的推理。例1、试根据等式的性质猜想不等式的性质。等式的性质:
(1) a=b?a+c=b+c;
(2) a=b? ac=bc;
(3) a=b?a2=b2;等等。猜想不等式的性质:问:这样猜想出的结论是否一定正确?可能存在生命火星上有生命吗?二者特征对比:类比推理的一般步骤:⑴ 观察发现类比对象;
⑵ 用一类对象的已知特征去推测另一类对象与之相应的特征,从而得出一个猜想。观察、比较联想、类推猜想新结论类比推理的特点:
1.类比是从A事物的已知属性,推测B事物的未知属性, 以旧有的认识为基础,类比出新的结果.
2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.
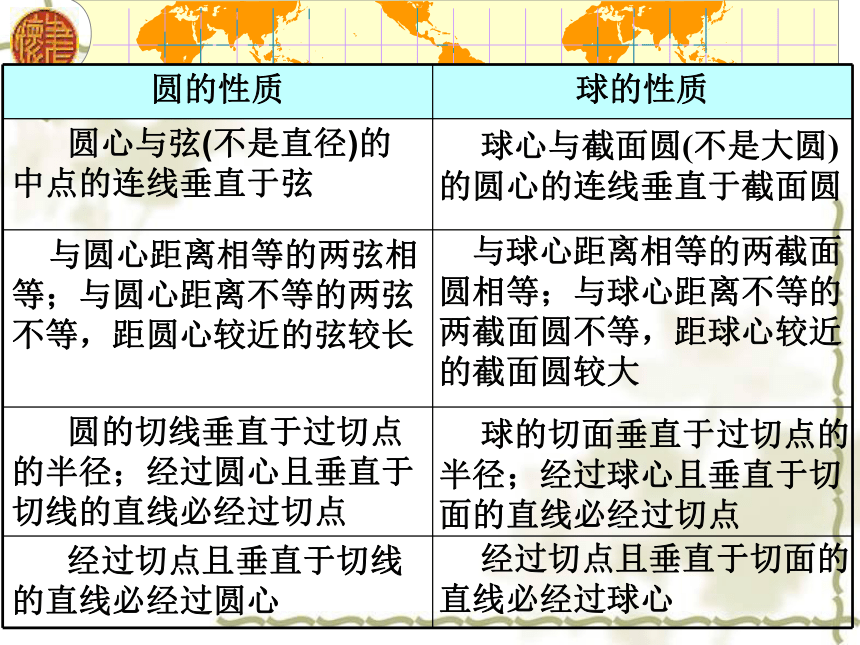
3.类比的结果是猜测的不一定可靠,但它却有发现的功能.例2、试将平面上的圆与空间的球进行类比.圆的定义:
球的定义: 空间中到一个定点的距离等于定长的点的集合.圆
弦
直径周长
面积球
截面圆大圆表面积体积平面内到一个定点的距离等于定长的点的集合. 球心与截面圆(不是大圆)的圆心的连线垂直于截面圆 与球心距离相等的两截面圆相等;与球心距离不等的两截面圆不等,距球心较近的截面圆较大 球的切面垂直于过切点的半径;经过球心且垂直于切面的直线必经过切点 经过切点且垂直于切面的直线必经过球心圆的有关运算球的有关运算以点(x0,y0)为圆心, r为半径
的圆的方程为
(x-x0)2+(y-y0)2 = r2以点(x0,y0,z0)为球心,
r为半径的球的方程为
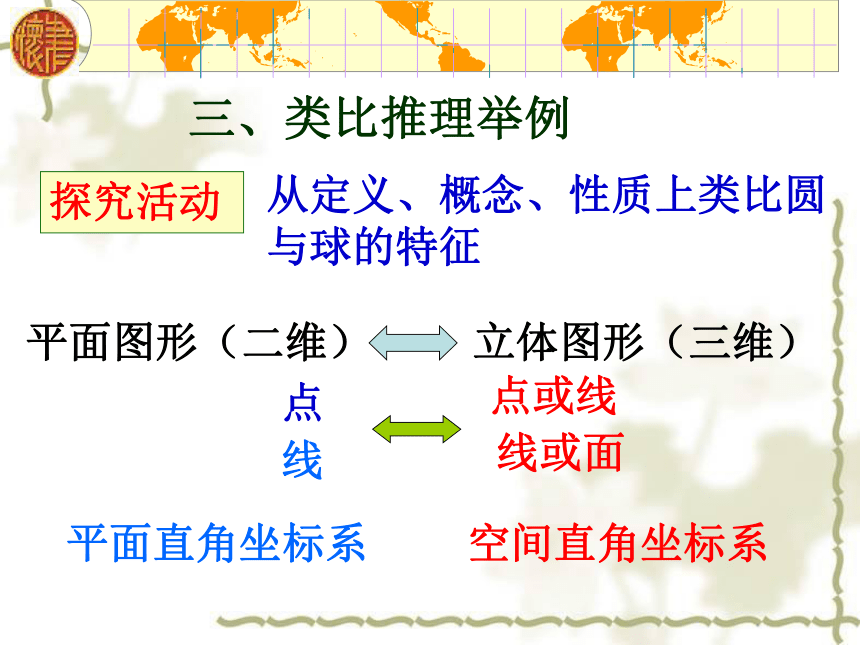
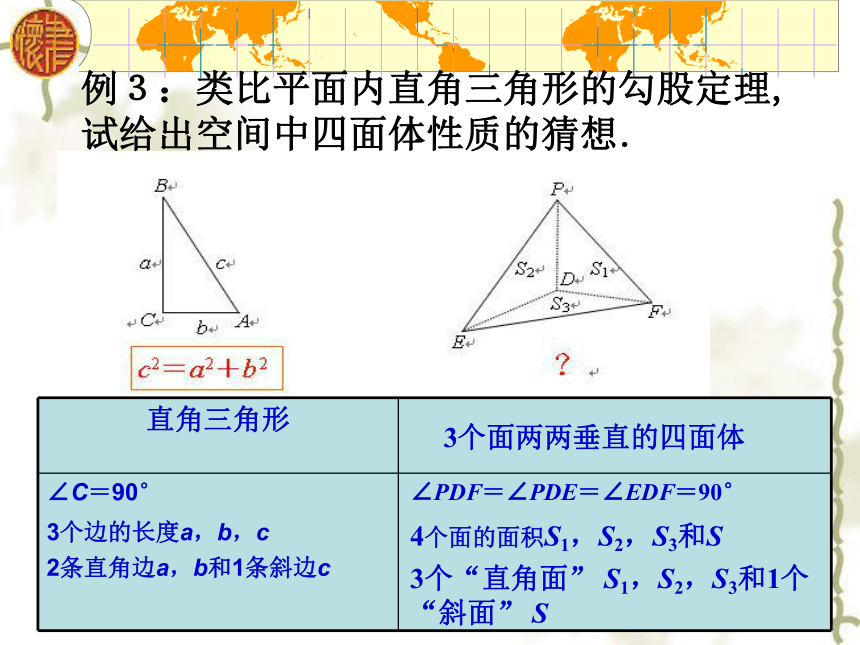
(x-x0)2+(y-y0)2+(z-z0)2 = r2球的体积球的表面积圆的周长 圆的面积平面图形(二维)立体图形(三维)点点或线线线或面平面直角坐标系空间直角坐标系三、类比推理举例例3:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S例题讲解c2=a2+b2几何中常见的类比对象三角形四面体(各面均为三角形)四边形六面体(各面均为四边形)圆球代数中常见的类比对象等差数列等比数列方程函数不等式交集,并集,补集或,且,非运算例4:设M,N是椭圆上关于原点对称的两点,点P是椭圆上任意一点,当直线PM,PN的斜率存在时,则KPM与KPN的积为与点P无关的定值。试对双曲线写出类似的性质并加以证明。类似性质为:设M,N是双曲线上关于原点对称的两点,点P是双曲线上任意一点,当直线PM,PN的斜率存在时,则KPM与KPN的积为与点P无关的定值。证明:设三点坐标分别为,则有求差得斜率积所以对应斜率的积是常数。练习1:(2005年全国)计算机中常用的十六进位制是逢16进1的计算制,采用数字0-9和字母A-F共16个计数符号,这些符号与十进制的数的对应关系如下表;例如用16进位制表示E+D=1B,则A×B=( )AA.6E B.72 C.5F D.0B图(1)图(2)练习2 类比推理:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.(简称:类比)四、小结1、类比推理的定义:2、类比推理的特点:1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.即类比推理是由特殊到特殊的推理.3.类比的结果是猜测性的不一定可靠,但它却有发现的功能.观察、比较联想、类推猜想新结论3、类比推理的一般步骤:4、类比推理的一般模式:所以B类事物可能具有性质d’.A类事物具有性质a,b,c,d,B类事物具有性质a’,b’,c’,(a,b,c与a’,b’,c’相似或相同)⑴ 观察发现类比对象;
⑵ 用一类对象的已知特征去推测另一类对象与之相应的特征,从而得出一个猜想。
类比推理具有“可靠性和猜想性”。归纳推理和类比推理的共同点 归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.合情推理 通俗地说,合情推理是指“合乎情理”的推理。合情推理的作用 数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论。 证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向作业:
(1)类比平面向量与空间向量的性质
(2)类比等差数列与等比数列的性质B例4.在平面上,设ha,hb,hc是三角形ABC三条边上的高,P为三角形内任一点,P到相应三边的距离分别为pa,pb,pc,我们可以得到结论:
试通过类比,写出在空间中的类似结论.ABCPpapbpcABCDP①②③④⑤⑥若 , 则 ①②③④⑤⑥若 , 则 ⑦⑦利用平面向量的性质类比得空间向量的性质利用等差数列性质类比等比数列性质n+m=p+q时,
am+an= ap+aqn+m=p+q时,
aman= apaq任意实数a、b都有等差中项 ,为当且仅当a、b同号时才有等比中项 ,为成等差数列成等比数列序号等差,项等差序号等差,项等比平面与空间中的余弦定理平面:三角形ABC中,空间:四面体A-BCD中,设二面角B-AC-D,C-AD-B,D-AB-C的大小依次为1.(03年新课程)在平面几何里,有勾股定理:
“设△ABC的两边AB、AC互相垂直,
则AB2+AC2=BC2.” 拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则
.练习1
归纳所得的结论是尚属未知的一般现象,
该结论超越了前提所包容的范围。(2)归纳推理得到结论的真实性需要经过证明
或实践检验。(3)归纳推理是一种具有创造性的推理。通过
归纳法得到的猜想,可以作为进一步研究
的起点,它帮助人们发现问题和提出问题。复习归纳推理的特点: 传说鲁班一次去林中伐木时被一株齿形的茅草划破了手。
是什么东西这么锋利?
他认真研究了该茅草的结构特点,原来草的边沿带有细且密的小齿,联想到自己的伐木工作,他喜出望外,何不制造一种带齿的工具来伐木?
这桩倒霉事使他发明了锯子。这个推理过程是归纳推理吗?二、类比推理的定义 两类对象具有某些类似特征,由其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.
类比推理是由特殊到特殊的推理。例1、试根据等式的性质猜想不等式的性质。等式的性质:
(1) a=b?a+c=b+c;
(2) a=b? ac=bc;
(3) a=b?a2=b2;等等。猜想不等式的性质:问:这样猜想出的结论是否一定正确?可能存在生命火星上有生命吗?二者特征对比:类比推理的一般步骤:⑴ 观察发现类比对象;
⑵ 用一类对象的已知特征去推测另一类对象与之相应的特征,从而得出一个猜想。观察、比较联想、类推猜想新结论类比推理的特点:
1.类比是从A事物的已知属性,推测B事物的未知属性, 以旧有的认识为基础,类比出新的结果.
2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.
3.类比的结果是猜测的不一定可靠,但它却有发现的功能.例2、试将平面上的圆与空间的球进行类比.圆的定义:
球的定义: 空间中到一个定点的距离等于定长的点的集合.圆
弦
直径周长
面积球
截面圆大圆表面积体积平面内到一个定点的距离等于定长的点的集合. 球心与截面圆(不是大圆)的圆心的连线垂直于截面圆 与球心距离相等的两截面圆相等;与球心距离不等的两截面圆不等,距球心较近的截面圆较大 球的切面垂直于过切点的半径;经过球心且垂直于切面的直线必经过切点 经过切点且垂直于切面的直线必经过球心圆的有关运算球的有关运算以点(x0,y0)为圆心, r为半径
的圆的方程为
(x-x0)2+(y-y0)2 = r2以点(x0,y0,z0)为球心,
r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2 = r2球的体积球的表面积圆的周长 圆的面积平面图形(二维)立体图形(三维)点点或线线线或面平面直角坐标系空间直角坐标系三、类比推理举例例3:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S例题讲解c2=a2+b2几何中常见的类比对象三角形四面体(各面均为三角形)四边形六面体(各面均为四边形)圆球代数中常见的类比对象等差数列等比数列方程函数不等式交集,并集,补集或,且,非运算例4:设M,N是椭圆上关于原点对称的两点,点P是椭圆上任意一点,当直线PM,PN的斜率存在时,则KPM与KPN的积为与点P无关的定值。试对双曲线写出类似的性质并加以证明。类似性质为:设M,N是双曲线上关于原点对称的两点,点P是双曲线上任意一点,当直线PM,PN的斜率存在时,则KPM与KPN的积为与点P无关的定值。证明:设三点坐标分别为,则有求差得斜率积所以对应斜率的积是常数。练习1:(2005年全国)计算机中常用的十六进位制是逢16进1的计算制,采用数字0-9和字母A-F共16个计数符号,这些符号与十进制的数的对应关系如下表;例如用16进位制表示E+D=1B,则A×B=( )AA.6E B.72 C.5F D.0B图(1)图(2)练习2 类比推理:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.(简称:类比)四、小结1、类比推理的定义:2、类比推理的特点:1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.即类比推理是由特殊到特殊的推理.3.类比的结果是猜测性的不一定可靠,但它却有发现的功能.观察、比较联想、类推猜想新结论3、类比推理的一般步骤:4、类比推理的一般模式:所以B类事物可能具有性质d’.A类事物具有性质a,b,c,d,B类事物具有性质a’,b’,c’,(a,b,c与a’,b’,c’相似或相同)⑴ 观察发现类比对象;
⑵ 用一类对象的已知特征去推测另一类对象与之相应的特征,从而得出一个猜想。
类比推理具有“可靠性和猜想性”。归纳推理和类比推理的共同点 归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.合情推理 通俗地说,合情推理是指“合乎情理”的推理。合情推理的作用 数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论。 证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向作业:
(1)类比平面向量与空间向量的性质
(2)类比等差数列与等比数列的性质B例4.在平面上,设ha,hb,hc是三角形ABC三条边上的高,P为三角形内任一点,P到相应三边的距离分别为pa,pb,pc,我们可以得到结论:
试通过类比,写出在空间中的类似结论.ABCPpapbpcABCDP①②③④⑤⑥若 , 则 ①②③④⑤⑥若 , 则 ⑦⑦利用平面向量的性质类比得空间向量的性质利用等差数列性质类比等比数列性质n+m=p+q时,
am+an= ap+aqn+m=p+q时,
aman= apaq任意实数a、b都有等差中项 ,为当且仅当a、b同号时才有等比中项 ,为成等差数列成等比数列序号等差,项等差序号等差,项等比平面与空间中的余弦定理平面:三角形ABC中,空间:四面体A-BCD中,设二面角B-AC-D,C-AD-B,D-AB-C的大小依次为1.(03年新课程)在平面几何里,有勾股定理:
“设△ABC的两边AB、AC互相垂直,
则AB2+AC2=BC2.” 拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则
.练习1
