直线的方程(1)课件[上学期]
图片预览






文档简介
课件15张PPT。欢迎指导!新沂市第二中学 胡芝艳欢迎指导!欢迎指导!欢迎指导!欢迎指导新沂二中 胡芝艳 一 情景设置1、直线的位置可以如何确定? ⑴、两点 2、若直线L经过点A(-1,3)斜率为-2,点P在直线L上运动,那么点P的坐标(x,y)满足什么条件?(1)、P(x,y)不同于A时,
(2)、P(x,y)与A重合时,x=-1,y=3也满足上式。⑵、一个点和一个方向即平面解析几何初步2.1.2 直线的方程(1)
一般地,设直线L经过已知点P1(x1,y1),并且它的斜率是k,
0xyl ①当点P(x,y)是直线L上不同于P1的任意一点时。根据经过两点的直线斜率公式,得二 建构数学:②当P点与P1重合时,有x=x1,y=y1,此时满足y-y1=k(x
-x1),所以直线L上所有点的坐标都满足y-y1=k(x-x1),
③不在直线L上的点,显然不满足(y-y1)/(x-x1)=k 即
不满足y-y1=k(x-x1),因此y-y1=k(x-x1)是直线L的方程。
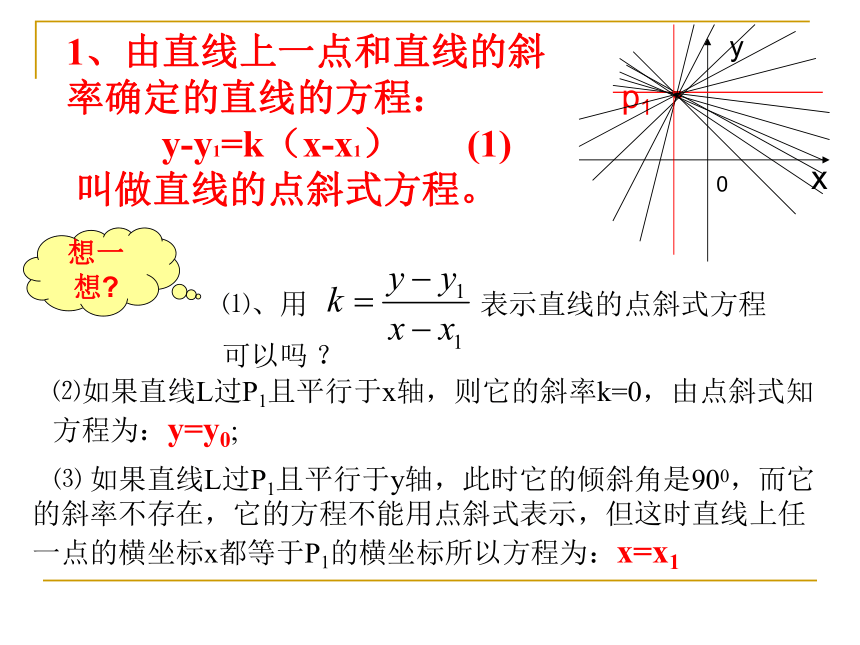
直线上任意一点P的坐标是(x,y),1、由直线上一点和直线的斜率确定的直线的方程:
y-y1=k(x-x1) (1)
叫做直线的点斜式方程。 ⑶ 如果直线L过P1且平行于y轴,此时它的倾斜角是900,而它的斜率不存在,它的方程不能用点斜式表示,但这时直线上任一点的横坐标x都等于P1的横坐标所以方程为:x=x1⑵如果直线L过P1且平行于x轴,则它的斜率k=0,由点斜式知方程为:y=y0;⑴、用 表示直线的点斜式方程可以吗 ?xy0·p1想一想?应用数学:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2, 即x-y + 5 = 00xy-55.P1⑶、一条直线经过点A(0,5),倾斜角为00;求下列直线的方程:
⑴、经过点(4,-2),斜率为3;
⑵、斜率为 /2,与X轴交点的横坐标为-7;
y= (x+7)/20xy5. y=53x-y-14=0动动手.⑷已知直线L的斜率是k,与y轴的交点是P(0,b),求直线方程。解:代入点斜式方程,得直线L的方程: y - b =k( x - 0)即 y = k x + b (2)2、我们把直线L与y轴交点(0,b)的纵坐标b叫做直线 L在y轴上的截距。方程(2)由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。想一想:⑴、方程(2)你以前见过吗?⑵、当直线的倾斜角为00时,直线方程如何表示?3⑶、倾斜角为900时,直线能用斜截式表示吗?⑷、截距就是距离,对吗?y=bx=x1例2:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4 即5 x - y + 4 = 0应用数学:动动手:写出下列直线的斜截式方程:(1)、斜率为-2,在y轴上截距为-2;(2)、与y轴交于(0,-2),倾斜角为450 。y=-2x-2y= x-2例3:已知直线L过A(3,-5)和B(-2,5), 求直线L的方程。解:∵直线L过点A(3,-5)和B(-2,5)将A(3,-5),k=-2代入点斜式,得y-(-5) =-2 ( x-3 )
即 2x + y -1 = 0解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1 例4:求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程。
直线过点(1,2)代入点斜式方程得y- 2 = x - 1 或y-2=-(x-1)即x-y+1=0或x+y-1=0四、练习巩固1、根据下列条件,分别写出直线的方程:
(1)、经过点(3,1),斜率为1/2;(2)、过点P(2,-4)倾斜角为900;(3)、过点(1,2),且斜率与直线
y=-2x+3的斜率相等。2、直线y=k(x+1) (k>0)的图象可能是( )XXXXYYYY0000111-1-1(A)(B)(C)(D)BX-2y-1=0X=2y=-2x+43、直线方程可表示成点斜式方程的条件是( )(A)直线的斜率存在
(B)直线的斜率不存在
(C)直线不过原点
(D)不同于上述答案A1、在同一直角坐标系中作出直线y=2, y=x+2, y=-x+2, y=3x+2, y=-3x+2,根据所作的直线,你能推测直线y=kx+2有什么特点吗?2、在同一直角坐标系中作出直线y=2x,y=2x+1, y=2x-1, y=2x+4, y=2x-4,根据所作的直线,你能推测直线y=2x+b有什么特点吗?xxyy002思考:
1、已知直线上的一点和直线的斜率可以 写出直线的点斜式方程:y-y1=k(x-x1)2、若是知道直线的斜率和直线在y轴上的截距可以写出直线的斜截式方程:y=kx+b3、直线的斜率不存在,若知道直线过一定点,则直线的方程为:x=x1六、作业:课本第79页 习题2.1(1) 第1、2题五、课堂小结:谢谢再见
(2)、P(x,y)与A重合时,x=-1,y=3也满足上式。⑵、一个点和一个方向即平面解析几何初步2.1.2 直线的方程(1)
一般地,设直线L经过已知点P1(x1,y1),并且它的斜率是k,
0xyl ①当点P(x,y)是直线L上不同于P1的任意一点时。根据经过两点的直线斜率公式,得二 建构数学:②当P点与P1重合时,有x=x1,y=y1,此时满足y-y1=k(x
-x1),所以直线L上所有点的坐标都满足y-y1=k(x-x1),
③不在直线L上的点,显然不满足(y-y1)/(x-x1)=k 即
不满足y-y1=k(x-x1),因此y-y1=k(x-x1)是直线L的方程。
直线上任意一点P的坐标是(x,y),1、由直线上一点和直线的斜率确定的直线的方程:
y-y1=k(x-x1) (1)
叫做直线的点斜式方程。 ⑶ 如果直线L过P1且平行于y轴,此时它的倾斜角是900,而它的斜率不存在,它的方程不能用点斜式表示,但这时直线上任一点的横坐标x都等于P1的横坐标所以方程为:x=x1⑵如果直线L过P1且平行于x轴,则它的斜率k=0,由点斜式知方程为:y=y0;⑴、用 表示直线的点斜式方程可以吗 ?xy0·p1想一想?应用数学:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2, 即x-y + 5 = 00xy-55.P1⑶、一条直线经过点A(0,5),倾斜角为00;求下列直线的方程:
⑴、经过点(4,-2),斜率为3;
⑵、斜率为 /2,与X轴交点的横坐标为-7;
y= (x+7)/20xy5. y=53x-y-14=0动动手.⑷已知直线L的斜率是k,与y轴的交点是P(0,b),求直线方程。解:代入点斜式方程,得直线L的方程: y - b =k( x - 0)即 y = k x + b (2)2、我们把直线L与y轴交点(0,b)的纵坐标b叫做直线 L在y轴上的截距。方程(2)由直线的斜率k与它在y轴上的截距b确定,所以方程(2)叫做直线的斜截式方程,简称斜截式。想一想:⑴、方程(2)你以前见过吗?⑵、当直线的倾斜角为00时,直线方程如何表示?3⑶、倾斜角为900时,直线能用斜截式表示吗?⑷、截距就是距离,对吗?y=bx=x1例2:斜率是5,在y轴上的截距是4的直线方程。解:由已知得k =5, b= 4,代入斜截式方程y= 5x + 4 即5 x - y + 4 = 0应用数学:动动手:写出下列直线的斜截式方程:(1)、斜率为-2,在y轴上截距为-2;(2)、与y轴交于(0,-2),倾斜角为450 。y=-2x-2y= x-2例3:已知直线L过A(3,-5)和B(-2,5), 求直线L的方程。解:∵直线L过点A(3,-5)和B(-2,5)将A(3,-5),k=-2代入点斜式,得y-(-5) =-2 ( x-3 )
即 2x + y -1 = 0解:∵直线与坐标轴组成一等腰直角三角形 ∴k=±1 例4:求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程。
直线过点(1,2)代入点斜式方程得y- 2 = x - 1 或y-2=-(x-1)即x-y+1=0或x+y-1=0四、练习巩固1、根据下列条件,分别写出直线的方程:
(1)、经过点(3,1),斜率为1/2;(2)、过点P(2,-4)倾斜角为900;(3)、过点(1,2),且斜率与直线
y=-2x+3的斜率相等。2、直线y=k(x+1) (k>0)的图象可能是( )XXXXYYYY0000111-1-1(A)(B)(C)(D)BX-2y-1=0X=2y=-2x+43、直线方程可表示成点斜式方程的条件是( )(A)直线的斜率存在
(B)直线的斜率不存在
(C)直线不过原点
(D)不同于上述答案A1、在同一直角坐标系中作出直线y=2, y=x+2, y=-x+2, y=3x+2, y=-3x+2,根据所作的直线,你能推测直线y=kx+2有什么特点吗?2、在同一直角坐标系中作出直线y=2x,y=2x+1, y=2x-1, y=2x+4, y=2x-4,根据所作的直线,你能推测直线y=2x+b有什么特点吗?xxyy002思考:
1、已知直线上的一点和直线的斜率可以 写出直线的点斜式方程:y-y1=k(x-x1)2、若是知道直线的斜率和直线在y轴上的截距可以写出直线的斜截式方程:y=kx+b3、直线的斜率不存在,若知道直线过一定点,则直线的方程为:x=x1六、作业:课本第79页 习题2.1(1) 第1、2题五、课堂小结:谢谢再见
