河南省濮阳市名校2022-2023学年高一下学期6月月考数学试题(含答案)
文档属性
| 名称 | 河南省濮阳市名校2022-2023学年高一下学期6月月考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 04:40:20 | ||
图片预览



文档简介
濮阳市名校2022-2023学年高一下学期6月月考
数学试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若把数据,改变为,则它们的( )
A.平均数与方差均不改变 B.平均数改变,方差保持不变
C.平均数不变,方差改变 D.平均数与方差均改变
3.向量,,,若A,B,C三点共线,则k的值为( )
A.-2 B.11 C.-2或11 D.2或11
4.若m,n是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,则
B.若,,则
C.若,,,,则
D.若,,,则
5.国家射击运动员甲在某次训练中10次射击成绩(单位:环)如下:7,5,9,7,4,8,9,9,7,5,则下列关于这组数据说法不正确的是( )
A.第70百分位数为8 B.平均数为7
C.方差为 D.众数为7和9
6.“五月的风”是坐落在山东省青岛市五四广场的标志性雕塑,重达500余吨,是我国目前最大的钢质城市雕塑,如图所示.现测量该雕塑的高度时,选取了与该雕塑底B在同一水平面内的两个测量基点C与D,测得,,,在C点测得该雕塑顶端A的仰角为40°,则该雕塑的高度约为(参考数据:取)( )
A.26m B.28m C.30m D.32m
7.在三棱锥中,平面ABC,,且,,,若球O在三棱锥的内部且与四个面都相切(称球O为三棱锥的内切球),则球O的表面积为( )
A. B. C. D.
8.十七世纪法国数学家、被誉为业余数学家之王的皮埃尔·德·费马提出了一个著名的几何问题:已知一个三角形,求作一点,使其与这个三角形的三个顶点的距离之和最小.它的答案是:当三角形的三个角均小于120°时,所求的点为三角形的正等角中心,即该点与三角形的三个顶点的连线两两成120°角;当三角形有一内角大于或等于120°时,所求点为三角形最大内角的顶点,在费马问题中所求的点称为费马点.已知a,b,c分别是三个内角A,B,C的对边,且,,若点P为的费马点,则( )
A.-2 B.-3 C.-4 D.-6
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下面是关于复数的四个命题,其中真命题为( )
A. B.
C.z的共轭复数为 D.z的虚部为-1
10.广东某高校为传承粤语文化,举办了主题为“粤唱粤美好”的校园粤语歌手比赛,在比赛中由A,B两个评委小组(各9人)给参赛选手打分.根据两个评委小组对同一名选手的打分绘制成如图所示折线图,则下列说法正确的是( )
A.A组打分的众数为47 B.B组打分的中位数为75
C.A组的意见相对一致 D.B组打分的均值小于A组打分的均值
11.记的内角A,B,C的对边分别为a,b,c,,,则( )
A.为钝角三角形 B.C为最大的内角
C. D.
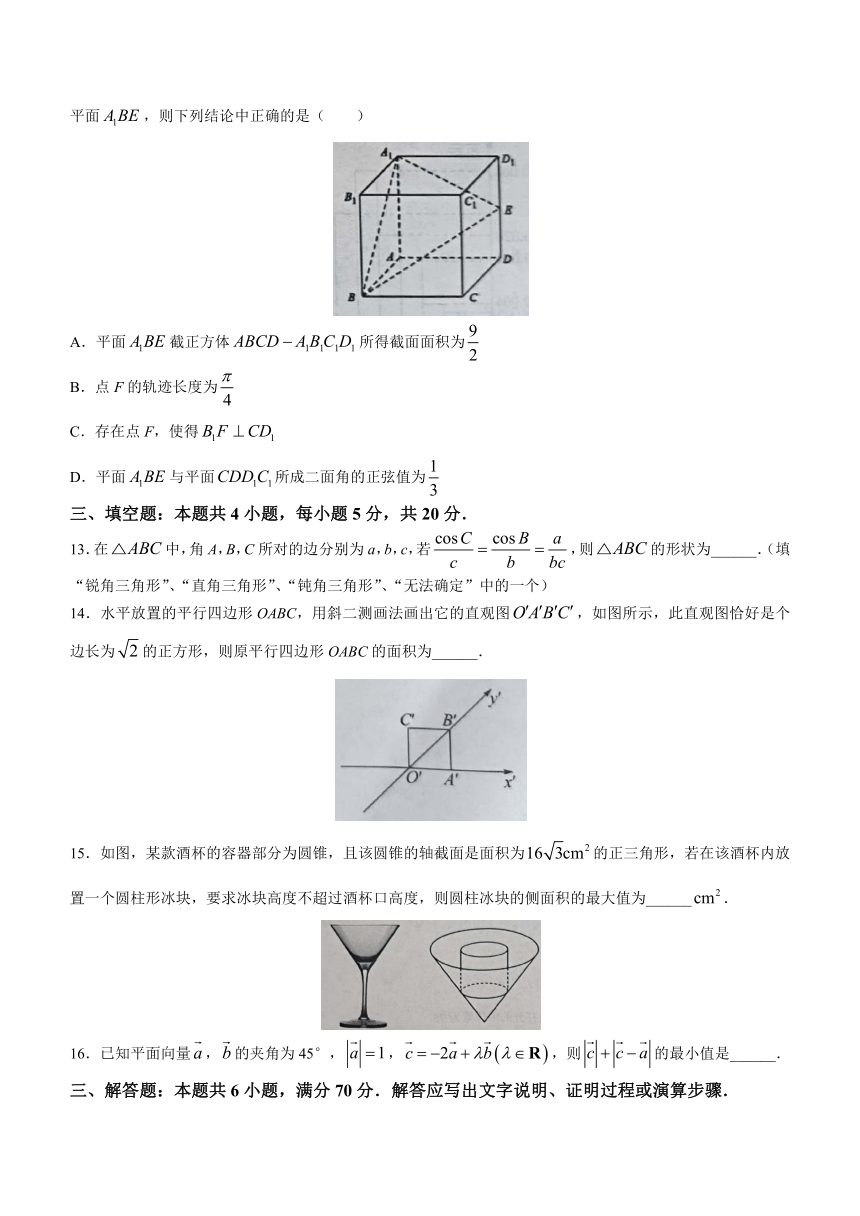
12.如图,正方体的棱长为2,E是棱的中点,F是侧面上的动点,且满足平面,则下列结论中正确的是( )
A.平面截正方体所得截面面积为
B.点F的轨迹长度为
C.存在点F,使得
D.平面与平面所成二面角的正弦值为
三、填空题:本题共4小题,每小题5分,共20分.
13.在中,角A,B,C所对的边分别为a,b,c,若,则的形状为______.(填“锐角三角形”、“直角三角形”、“钝角三角形”、“无法确定”中的一个)
14.水平放置的平行四边形OABC,用斜二测画法画出它的直观图,如图所示,此直观图恰好是个边长为的正方形,则原平行四边形OABC的面积为______.
15.如图,某款酒杯的容器部分为圆锥,且该圆锥的轴截面是面积为的正三角形,若在该酒杯内放置一个圆柱形冰块,要求冰块高度不超过酒杯口高度,则圆柱冰块的侧面积的最大值为______.
16.已知平面向量,的夹角为45°,,,则的最小值是______.
三、解答题:本题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)新冠肺炎疫情期间,某地为了解本地居民对当地防疫工作的满意度,从本地居民中随机抽取若干居民进行评分(满分为100分),根据调查数据制成如下频率分布直方图.
(1)求频率分布直方图中a的值;
(2)根据频率分布直方图估计本次评测分数的平均数(同一组中的数据用该组区间的中点值作代表,并精确到0.1).
18.(本小题12分)已知平面向量,满足,,,且.
(1)求;
(2)设向量,,记,求的值.
19.(本小题12分)如图所示,在正六棱锥中,O为底面中心,,.
(1)求该正六棱锥的体积和侧面积;
(2)若该正六棱锥的顶点都在球M的表面上,求球M的表面积和体积.
20.(本小题12分)在中,.
(1)求A;
(2)若点D在BC边上,,,求的面积.
21.(本小题12分)如图,在直角梯形OABC中,,,.F为AB上靠近B的三等分点,OF交AC于D,E为线段BC上的一个动点(包含端点).
(1)若,求实数t的值;
(2)设,求的取值范围.
22.(本小题12分)如图所示,正四棱锥中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,问在棱AD上是否存在一点F,使侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
濮阳市名校2022-2023学年高一下学期6月月考
数学试卷参考答案
一、二、选择题
1 2 3 4 5 6 7 8 9 10 11 12
D B C D A C A B BD AC BC AC
8.解析:,
即 ,
又 ,
,
即 ,
, 又.
由三角形内角和性质知:△ABC内角均小于120°,结合题设易知:P点一定在三角形的内部,
再由余弦定理知, ,,
,
.
由等号左右两边同时乘以可得:
,
.
三、填空题
13.直角三角形14.15.16.
四、解答题
17.解析:(1),
. .....................................................4分
平均数为
. ...10分
18.解析:(1)由题知,..............1分
所以;..............5分
(2)因为,..............7分
,同理可求得,..............10分
所以................................12分
19.解析:(1)由条件可知正六边形ABCDEF的边长为4,
所以底面积为,
该正六棱锥的体积为,...............................3分
正六棱锥的侧棱长为,
侧面等腰三角形的面积为,
故该正六棱锥的侧面积为;...............................6分
(2)球心M一定在直线SO上,设球M的半径为R,
则,又,
所以,解得, ...............................8分
所以球M的表面积为,..............................10分
体积为................................12分
20.解析:(1)由正弦定理边角互化可知,,即,
所以,...............................4分
又,所以;...............................5分
(2)点是的中点,
,即(Ⅰ).................7分
,即,...............................9分
化简为,即,(Ⅱ)
由(Ⅰ)(Ⅱ)两式可得,...............................10分
所以................................12分
21.解析:(1)由题意得,
则
故,由共起点的三向量终点共线的充要条件知,
,则;...............................4分
(2)由已知,
因P是线段BC上动点,则令,.........................5分
,........7分
又,不共线,则有,
,
在上递增,...........................10分
所以,,,
故的取值范围是. ..............................12分
22.解析:(1)取的中点,连接、,
由正四棱锥的性质可知平面,平面,则,
依条件可知,则为所求二面角的平面角. ...........2分
面,则为侧棱与底面所成的角,
则,设,则,所以,,
则,因为,故. ............5分
(2)延长交于,则为的中点,取的中点,连接、.
因为,为的中点,则,
同理可得,
,故平面,
平面,
平面平面,.................7分
又,,
所以,为正三角形,为的中点,则,
又因为平面平面,平面平面,平面,
所以,平面,.................10分
取的中点,连接,
、分别为、的中点,则且,
因为且,、分别为、的中点,则且,
为的中点,则且,故且,
所以,四边形为平行四边形,则,故⊥平面.
因此,是的四等分点,靠近A点的位置. ..........................12分
数学试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若把数据,改变为,则它们的( )
A.平均数与方差均不改变 B.平均数改变,方差保持不变
C.平均数不变,方差改变 D.平均数与方差均改变
3.向量,,,若A,B,C三点共线,则k的值为( )
A.-2 B.11 C.-2或11 D.2或11
4.若m,n是两条不同的直线,,是两个不同的平面,则下列命题正确的是( )
A.若,,则
B.若,,则
C.若,,,,则
D.若,,,则
5.国家射击运动员甲在某次训练中10次射击成绩(单位:环)如下:7,5,9,7,4,8,9,9,7,5,则下列关于这组数据说法不正确的是( )
A.第70百分位数为8 B.平均数为7
C.方差为 D.众数为7和9
6.“五月的风”是坐落在山东省青岛市五四广场的标志性雕塑,重达500余吨,是我国目前最大的钢质城市雕塑,如图所示.现测量该雕塑的高度时,选取了与该雕塑底B在同一水平面内的两个测量基点C与D,测得,,,在C点测得该雕塑顶端A的仰角为40°,则该雕塑的高度约为(参考数据:取)( )
A.26m B.28m C.30m D.32m
7.在三棱锥中,平面ABC,,且,,,若球O在三棱锥的内部且与四个面都相切(称球O为三棱锥的内切球),则球O的表面积为( )
A. B. C. D.
8.十七世纪法国数学家、被誉为业余数学家之王的皮埃尔·德·费马提出了一个著名的几何问题:已知一个三角形,求作一点,使其与这个三角形的三个顶点的距离之和最小.它的答案是:当三角形的三个角均小于120°时,所求的点为三角形的正等角中心,即该点与三角形的三个顶点的连线两两成120°角;当三角形有一内角大于或等于120°时,所求点为三角形最大内角的顶点,在费马问题中所求的点称为费马点.已知a,b,c分别是三个内角A,B,C的对边,且,,若点P为的费马点,则( )
A.-2 B.-3 C.-4 D.-6
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下面是关于复数的四个命题,其中真命题为( )
A. B.
C.z的共轭复数为 D.z的虚部为-1
10.广东某高校为传承粤语文化,举办了主题为“粤唱粤美好”的校园粤语歌手比赛,在比赛中由A,B两个评委小组(各9人)给参赛选手打分.根据两个评委小组对同一名选手的打分绘制成如图所示折线图,则下列说法正确的是( )
A.A组打分的众数为47 B.B组打分的中位数为75
C.A组的意见相对一致 D.B组打分的均值小于A组打分的均值
11.记的内角A,B,C的对边分别为a,b,c,,,则( )
A.为钝角三角形 B.C为最大的内角
C. D.
12.如图,正方体的棱长为2,E是棱的中点,F是侧面上的动点,且满足平面,则下列结论中正确的是( )
A.平面截正方体所得截面面积为
B.点F的轨迹长度为
C.存在点F,使得
D.平面与平面所成二面角的正弦值为
三、填空题:本题共4小题,每小题5分,共20分.
13.在中,角A,B,C所对的边分别为a,b,c,若,则的形状为______.(填“锐角三角形”、“直角三角形”、“钝角三角形”、“无法确定”中的一个)
14.水平放置的平行四边形OABC,用斜二测画法画出它的直观图,如图所示,此直观图恰好是个边长为的正方形,则原平行四边形OABC的面积为______.
15.如图,某款酒杯的容器部分为圆锥,且该圆锥的轴截面是面积为的正三角形,若在该酒杯内放置一个圆柱形冰块,要求冰块高度不超过酒杯口高度,则圆柱冰块的侧面积的最大值为______.
16.已知平面向量,的夹角为45°,,,则的最小值是______.
三、解答题:本题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)新冠肺炎疫情期间,某地为了解本地居民对当地防疫工作的满意度,从本地居民中随机抽取若干居民进行评分(满分为100分),根据调查数据制成如下频率分布直方图.
(1)求频率分布直方图中a的值;
(2)根据频率分布直方图估计本次评测分数的平均数(同一组中的数据用该组区间的中点值作代表,并精确到0.1).
18.(本小题12分)已知平面向量,满足,,,且.
(1)求;
(2)设向量,,记,求的值.
19.(本小题12分)如图所示,在正六棱锥中,O为底面中心,,.
(1)求该正六棱锥的体积和侧面积;
(2)若该正六棱锥的顶点都在球M的表面上,求球M的表面积和体积.
20.(本小题12分)在中,.
(1)求A;
(2)若点D在BC边上,,,求的面积.
21.(本小题12分)如图,在直角梯形OABC中,,,.F为AB上靠近B的三等分点,OF交AC于D,E为线段BC上的一个动点(包含端点).
(1)若,求实数t的值;
(2)设,求的取值范围.
22.(本小题12分)如图所示,正四棱锥中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,问在棱AD上是否存在一点F,使侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.
濮阳市名校2022-2023学年高一下学期6月月考
数学试卷参考答案
一、二、选择题
1 2 3 4 5 6 7 8 9 10 11 12
D B C D A C A B BD AC BC AC
8.解析:,
即 ,
又 ,
,
即 ,
, 又.
由三角形内角和性质知:△ABC内角均小于120°,结合题设易知:P点一定在三角形的内部,
再由余弦定理知, ,,
,
.
由等号左右两边同时乘以可得:
,
.
三、填空题
13.直角三角形14.15.16.
四、解答题
17.解析:(1),
. .....................................................4分
平均数为
. ...10分
18.解析:(1)由题知,..............1分
所以;..............5分
(2)因为,..............7分
,同理可求得,..............10分
所以................................12分
19.解析:(1)由条件可知正六边形ABCDEF的边长为4,
所以底面积为,
该正六棱锥的体积为,...............................3分
正六棱锥的侧棱长为,
侧面等腰三角形的面积为,
故该正六棱锥的侧面积为;...............................6分
(2)球心M一定在直线SO上,设球M的半径为R,
则,又,
所以,解得, ...............................8分
所以球M的表面积为,..............................10分
体积为................................12分
20.解析:(1)由正弦定理边角互化可知,,即,
所以,...............................4分
又,所以;...............................5分
(2)点是的中点,
,即(Ⅰ).................7分
,即,...............................9分
化简为,即,(Ⅱ)
由(Ⅰ)(Ⅱ)两式可得,...............................10分
所以................................12分
21.解析:(1)由题意得,
则
故,由共起点的三向量终点共线的充要条件知,
,则;...............................4分
(2)由已知,
因P是线段BC上动点,则令,.........................5分
,........7分
又,不共线,则有,
,
在上递增,...........................10分
所以,,,
故的取值范围是. ..............................12分
22.解析:(1)取的中点,连接、,
由正四棱锥的性质可知平面,平面,则,
依条件可知,则为所求二面角的平面角. ...........2分
面,则为侧棱与底面所成的角,
则,设,则,所以,,
则,因为,故. ............5分
(2)延长交于,则为的中点,取的中点,连接、.
因为,为的中点,则,
同理可得,
,故平面,
平面,
平面平面,.................7分
又,,
所以,为正三角形,为的中点,则,
又因为平面平面,平面平面,平面,
所以,平面,.................10分
取的中点,连接,
、分别为、的中点,则且,
因为且,、分别为、的中点,则且,
为的中点,则且,故且,
所以,四边形为平行四边形,则,故⊥平面.
因此,是的四等分点,靠近A点的位置. ..........................12分
同课章节目录
