数学人教A版(2019)必修第二册9.1.1简单随机抽样(共47张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册9.1.1简单随机抽样(共47张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 20:48:42 | ||
图片预览










文档简介
(共47张PPT)
(第一课时)
9.1.1 简单随机抽样
简单随机抽样定义
一天,妈妈叫儿子去买一盒饼。临出门前嘱咐儿子要买咸口味的饼。儿子拿着钱出门了,过了好一会儿,儿子才回到家。
“都是咸口味的吗?”妈妈问。
“都是咸口味的。”
“你这么肯定?”
儿子递过一盒空的饼盒,兴奋地说:
“我每个都尝过啦。”
— 开心小故事 —
简单随机抽样定义
思考①
在这则笑话中,儿子采用的是什么调查方式?
思考②
思考:你知道我国有哪些数据是普查的吗?
普查:对每一个调查对象都进行调查的方法,称为全面调查。
人口普查,经济普查,农业普查,工业普查
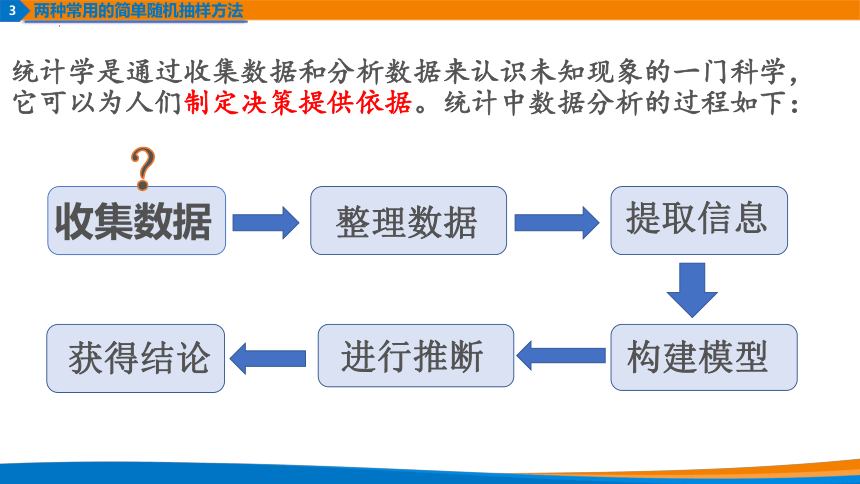
统计学是通过收集数据和分析数据来认识未知现象的一门科学,它可以为人们制定决策提供依据。统计中数据分析的过程如下:
收集数据
整理数据
提取信息
构建模型
进行推断
获得结论
?
两种常用的简单随机抽样方法
3
人口普查流程:
一、准备工作
二、摸底工作
三、登记工作
四、对比复查工作
五、质量控制工作
六、现场验收
2019年11月,经李克强总理签批,国务院印发《关于开展第七次全国人口普查的通知》。根据《中华人民共和国统计法》和《全国人口普查条例》规定,国务院决定于2020年开展第七次全国人口普查。普查标准时点是2020年11月1日零时,彻查人口出生变动情况以及房屋情况。
统计相关概念
1
普查
像人口普查这样,对每一个调查对象都进行调查的方法,称为全面调查,又叫普查.
我们把调查对象的全体称为总体,组成总体的每一个调查对象称为个体.
为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,
每一个调查对象的相应指标作为个体.
例.
在全国人口普查中:
总体:
个体:
全国所有居民.
每一个居民.
/全国所有居民的性别、年龄等.
/每一个居民的性别、年龄等.
思考1.
普查有何优缺点?
优点:数据全面
缺点:花费高、效率低,可能具有破坏性
统计相关概念
1
该调查方式为普查吗?
不是
抽样调查
为什么不进行普查?
统计相关概念
1
抽样调查
根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和推断的调查方法,称为抽样调查.
两种基本的抽样方法——
简单随机抽样
从总体中抽取的那部分个体称为样本,
样本中包含的个体数称为样本容量,简称样本量.
调查样本获得的变量值称为样本的观测数据,简称样本数据.
分层随机抽样
花费少,效率高
思考2
抽样调查有何优缺点?
你能举出一些适合用抽样调查的例子吗?
优点:花费少、效率高;缺点:结果与实际情况可能有误差
在一次数学课堂上,陈老师请四位同学列举出生活中运用全面调查或抽样调查的例子.
小凉:为了了解玉米种子的发芽情况,采用抽样调查.
小爽:为了了解全班同学是否给父母洗过脚,采用全面调查.
小夏:为了了解某批导弹的射程,采用全面调查.
小天:为了了解全国中学生安全自救知识的掌握情况,采用抽样调查.
你认为以上四位同学所列举的事例的调查方式错误的是
A.小凉 B.小爽 C.小夏 D.小天
例1
√
下列调查方式,你认为最合适的是
A.了解北京每天的流动人口数,采用抽样调查
B.旅客上飞机前的安检,采用抽样调查
C.了解北京居民“建党百年庆祝大会”期间的出行方式,采用全面调查
D.日光灯管厂要检测一批灯管的使用寿命,采用全面调查
跟踪训练1
√
9.1.1 简单随机抽样
假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同,你能通过抽样调查的方法估计袋中红球所占的比例吗?
放回的摸球
探究.
用摸到红球的频率估计口袋中红球所占的比例。
不放回的摸球
思考3
为什么能用摸到红球的频率估计口袋中红球所占的比例?
每一个小球被摸到的概率相等
简单随机抽样
2
放回摸球的效率高,还是不放回摸球的效率高?
思考4
不放回
简单随机抽样
2
简单随机抽样
一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤n<N)个个体作为样本,如果抽取是放回的,且每次抽取时总体内的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做放回简单随机抽样,如果抽取是不放回的,且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做不放回简单随机抽样.放回简单随机抽样和不放回简单随机抽样统称为简单随机抽样.通过简单随机抽样获得的样本称为简单随机样本.
说明:
1.除非特殊声明,本章所称的简单随机抽样指不放回简单随机抽样.
2.从总体中,逐个不放回地抽取n个个体作为样本和一次性抽取n个个体作为样本,两种方法是等价的.
各个个体被抽到的概率都相等
在简单随机抽样中,某一个个体被抽到的可能性
A.与第几次抽样有关,第一次抽到的可能性大一些
B.与第几次抽样无关,每次抽到的可能性都相等
C.与第几次抽样有关,最后一次抽到的可能性要大些
D.与第几次抽样无关,每次都是等可能地抽取,但各次抽取的可能性不
一定
例2
√
在简单随机抽样中,每一个个体被抽到的可能性都相等,与第几次抽样无关,故A,C,D不正确,B正确.
(2)从总体容量为N的一批零件中,通过简单随机抽样抽取一个容量为30的样本,若每个零件被抽到的可能性为0.25,则N的值为
A.120 B.200 C.150 D.100
√
两种简单随机抽样方法
3
1.抽签法
1.先给712名学生编号,例如按1~712进行编号.
编号
2.然后把所有编号写在外观、质地等无差别的小纸片(也可以是卡片、小球等)上作为号签,并将这些小纸片放在一个不透明的盒里,充分搅拌.最后从盒中不放回地逐个抽取号签.
3.使与号签上的编号对应的学生进入样本,直到抽足样本所需要的人数.
抽签
取样
一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级的平均身高,以便设定可调节课桌椅的标准高度。已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本?
例题
两种简单随机抽样方法
3
一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级的平均身高,以便设定可调节课桌椅的标准高度。已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本?
2.随机数法
1.先给712名学生编号,例如按1~712进行编号.
2.用随机数工具产生1~712范围内的整数随机数,把产生的随机数作为抽中的编号.
3.使与编号对应的学生进入样本.重复上述过程,直到抽足样本所需要的人数.
编号
产生随机数
取样
例题
两种简单随机抽样方法
3
思考5
如何生成随机数?
(1) 用随机试验生成随机数
准备10个大小、质地一样的小球,小球上分别写上数字0,1,2,3,…,9,把它们放入一个不透明的袋中.从袋中有放回摸取3次,每次摸取前充分搅拌,并把第一、二、三次摸到的数字分别作为百、十、个位数,这样就生成了一个三位随机数.如果这个三位数在1~712范围内,就代表对应编号的学生被抽中,否则舍弃编号.这样产生的随机数可能会有重复.
如果生成的随机数有重复,即同一编号被多次抽到,可以剔除重复的编号并重新产生随机数,直到产生的不同编号个数等于样本所需要的人数.
如果生成的随机数有重复,该如何解决?
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
①用计算器生成随机数
random随机的
integer
整数
该方法生成的随机数可能重复
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
②用电子表格软件生成随机数
该方法生成的随机数可能重复
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
③用R统计软件生成随机数
样本
不放回
该方法生成的随机数不重复
有放回
该方法生成的随机数可能重复
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
③用R统计软件生成随机数
除了上述软件以外,还有很多能够产生随机数的软件,
一般的抽签软件,如:抽签助手,抽签器等;
专业的统计软件,如:SAS,SPSS,S-Plus,State等;
综合性较强的数学软件,如:MATLAB,Mathematica,GeoGebra等.
小贴士
样本
不放回
两种简单随机抽样方法
3
抽样方法 优点 缺点
抽签法 简单易行 总体量较大时,
制作号签成本高,
“均匀搅拌”困难.
随机数法 利用信息技术产生随机数方便、快捷、效率高,可节省成本. 随机试验和部分软件可能会产生重复随机数,需要剔除重复编号并重新产生.
思考6
比较随机数法与抽签法,它们各有什么优点和缺点?
为了了解某校高三学生每天的作业量,通过简单随机抽样从该校高三学生中抽取了60名学生,通过调查发现这60名学生每天完成作业平均用时2小时,则可以推测该校高三学生每天完成作业所需时间的平均数
A.一定为2小时 B.高于2小时
C.低于2小时 D.约为2小时
跟踪训练4
√
样本平均数具有随机性,只能估计总体平均数.
两种简单随机抽样方法
3
思考7
用简单随机抽样的方法抽取样本,样本量是否越大越好?
对于样本的代表性,一般说来,样本量大的会好于样本量小的.
从调查的成本角度,样本量大会导致人力、费用、时间等成本的增加.
因此,抽样调查中样本量的选择要根据实际问题的需要,在精度和费用两者间进行权衡,
并不一定是越大越好.
两种简单随机抽样方法
3
练习
教材P177 练习1~4
1.在以下调查中,总体、个体各是什么?哪些适合用全面调查?哪些适合用抽样调查?
(1) 调查一个班级学生每周的体育锻炼时间;
(2) 调查一个地区结核病的发病率;
(3) 调查一批炮弹的杀伤半径;
(4) 调查一个水库所有鱼中草鱼所占的比例.
总体:全班学生,个体:这个班的每一位学生,
适合用全面调查.
总体:整个地区的居民,个体:这个地区的每一位居民,
适合用抽样调查.
总体:这批炮弹,个体:这批炮弹的每一个炮弹,
适合用抽样调查.
总体:这个水库里所有的鱼,个体:这个水库里的每一条鱼,
适合用抽样调查.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
变1.(多选)为了了解全校240名高一学生的身高情况,从中抽取了40名学生进行测量.下列说法正确的是
A.总体是240名学生 B.个体是每一名学生
C.样本是任意40名学生 D.样本容量是40
√
√
√
在这个问题中,总体是240名学生,个体是每一名学生,样本是抽取的40名学生,样本容量是40.
两种简单随机抽样方法
3
练习
教材P177 练习1~4
2.如图,由均匀材质制成的一个正20面体(每个面都是正三角形),将20个平面平分成10组,第1组标上0,第2组标上1,…,第10组标上9.
是;
是.
投掷正20面体,若把朝上一面的数字作为投掷结果,则出现0,1,2,…,9是等可能的吗?
(2) 三个正20面体分别涂上红、黄、蓝三种颜色,分别代表百位、十位、个位,同时投掷可以产生一个三位数(百位为0的也看作三位数),它是000~999范围内的随机数吗?
两种简单随机抽样方法
3
练习
教材P177 练习1~4
3.实验室的笼子里共有100只小白鼠,现要从中抽取10只作试验用.下列两种情况是否属于简单随机抽样?请说明理由.
(1) 每次不经任何挑选地抓一只,抓满10只为止;
(2) 将笼中的100只小白鼠按1~100编号,任意选出编号范围内的10个不重复数字,把相应编号的小白鼠作为试验用的小白鼠.
是,
每次抽取时,没进入样本的各个个体被抽到的概率相同,
不放回简单随机抽样;
是,
该抽样方法类等同于简单随机抽样中的抽签法.
两种简单随机抽样方法
3
练习
教材P177 练习1~4
4.如果计算器只能生成[0,1)内的随机数,你有办法把它转化为1~100范围内的整数随机数吗?转化为1~712范围内的整数随机数呢?
记r为生成的[0,1)内的随机数
则x为1~100范围内的整数随机数;
同理,令y为712r+1的整数部分,则y为1~712范围内的整数随机数.
令x为100r+1的整数部分,
(也可写作x=[100r+1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.从某批零件中抽取50个,然后再从抽取的50个中抽出40个进行合格检查,发现合格品有36个,则可以推测该批产品的合格率为
A.36% B.72% C.90% D.25%
√
问题1 下面是用随机数法从树人中学高一年级学生中抽取的一个容量为50的简单随机样本,他们的身高变量值(单位:cm)如下:
156.0 166.0 157.0 155.0 162.0 168.0 173.0 155.0 157.0 160.0
175.0 177.0 158.0 155.0 161.0 158.0 161.5 166.0 174.0 170.0
162.0 155.0 156.0 158.0 183.0 164.0 173.0 155.5 176.0 171.0
164.5 160.0 149.0 172.0 165.0 176.0 176.0 168.5 171.0 169.0
156.0 171.0 151.0 158.0 156.0 165.0 158.0 175.0 165.0 171.0
试求树人中学高一年级学生的平均身高大约为多少?
探究新知
解:由这些样本观测数据,我们可以计算出样本的平均数为
上面我们通过简单随机抽样得到部分学生的平均身高,并用样本平均身高来估计树人中学高一年级学生的平均身高.
由此可以估计树人中学高一年级学生的平均身高为164.3cm左右.
探究新知
4.总体平均数与样本平均数
(1)总体平均数:
一般地,总体中有N个个体,它们的变量值分别为 Y1,Y2,…,YN,则称 为总体均值,又称总体平均数.
频数
频率
探究新知
4.总体平均数与样本平均数
(1)总体平均数:
一般地,总体中有N个个体,它们的变量值分别为 Y1,Y2,…,YN,则称 为总体均值,又称总体平均数.
总体均值加权平均数的形式:
探究新知
(2)样本平均数:
如果从总体中抽取一个容量为n的样本,它们的变量值分别为 y1,y2,…,yn,则称 为样本均值,又称样本平均数.
样本均值加权平均数的形式:
例题讲解
例5 某公司的人员构成及工资数如下:
经理1人,周工资4000元;高层管理人员3人,周工资均为1000元;高级技工4人,周工资均为900元;工人6人,周工资均为700元;学徒1人,周工资为500元.计算该公司员工周工资的平均数.
探究新知
探究:小明想考察一下简单随机抽样的估计效果, 他从树人中学医务室得到了高一年级学生身高的所有数据, 计算出整个年级学生的平均身高为165.0cm. 然后, 小明用简单随机抽样的方法, 从这些数据中抽取了样本量为50和100的样本各10个, 分别计算出样本平均数, 如下表所示, 从小明多次抽样所得的结果中, 你有什么发现?
抽样序号 1 2 3 4 5 6 7 8 9 10
样本量为50的平均数 165.2 162.8 164.4 164.4 165.6 164.8 165.3 164.7 165.7 165.0
样本量为100的平均数 164.4 165.0 164.7 164.9 164.6 164.9 165.1 165.2 165.1 165.2
为了更方便地观察数据,以便我们分析样本平均数的特点以及与总体平均数的关系,我们把这20次试验的平均数用图形表示出来,如右图所示. 图中的红线表示树人中学高一年级全体学生身高的平均数.
探究新知
总体平均数是总体的一项重要特征. 另外,某类个体在总体中所占的比例也是人们关心的一项总体特征,例如全部产品中合格品所占的比例、赞成某项政策的人在整个人群中所占的比例等.
从试验结果看,不管样本量为50,还是为100,不同样本的平均数往往是不同的. 由于样本的选取是随机的,因此样本平均数也具有随机性,这与总体平均数是一个确定的数不同.
虽然在所有20个样本平均数中,与总体平均数完全一致的很少,但除了样本量为50的第2个样本外,样本平均数偏离总体平均数都不超过1cm,
即大部分样本平均数离总体平均数不远,在总体平均数附近波动.
比较样本量为50和样本量为100的样本平均数,还可以发现样本量为100的波动幅度明显小于样本量为50的,这与我们对增加样本量可以提高估计效果的认识是一致的.
探究新知
问题2 眼睛是心灵的窗户,保护好视力非常重要. 树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
全体学生构成调查的总体,每一位学生是个体,学生的视力是考察的变量.
为了便于问题的描述,我们记“视力不低于5.0”为1,“视力低于5.0”为0,则第i个(i=1,2,...,2174)学生的视力变量值为
探究新知
例如,现在,我们从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 1 1 1 0 1 1 0 1 1
1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0
由样本平均数,我们估计在树人中学全体学生中,“视力不低于5.0”的比例约为0.54.
探究新知
简单随机抽样的优缺点:
在实际应用中,简单随机抽样有一定局限性.
例如,当总体很大时,编号等准备工作耗费时间、人工,甚至难以做到;抽中个体较为分散,要找到样本中的个体进行调查会遇到很多困难;简单随机抽样没有其他辅助信息,估计效率不是很高.
简单随机抽样方法简单、直观,用样本平均数估计总体平均数也比较方便. 简单随机抽样是一种基本抽样方法,是其他抽样方法的基础.
因此,在规模较大的调查中,直接采用简单随机抽样的并不多,一般是把简单随机抽样和其他抽样方法组合使用.
优点:
缺点:
课堂练习
(1)计算芳芳上学期平时的平均成绩;(2)如果学期的总评成绩按右图所示的比例计算,请计算出芳芳该学期的总评成绩.
1.芳芳在九年级上学期的数学成绩如下表所示:
答:芳芳上学期平时的平均成绩是86分.
(2)86×10%+90×30%+85×60%=86.6.
答:芳芳该学期的总评成绩是86.6分.
测验类别 平时 期中考试 期末考试
测验1 测验2 测验3 测验4 成绩 88 72 98 86 90 85
2.已知一组数据x1, x2, x3, x4, x5的平均数是2,那么另一组数据2x1-1,2x2-1,2x3-1,2x4-1,2x5-1的平均数为________.
课堂练习
3
解析:因为数据x1, x2, x3, x4, x5的平均数是2,所以
所以数据2x1-1, 2x2-1,2x3-1,2x4-1,2x5-1的平均数为
探究新知
平均数的求解方法
(1)利用公式求解:平均数反映了一组数据的整体水平,平均数的大小与一组数据中每个数据均有联系,任何一个数据的变动都会相应引起平均数的变动. 所以求平均数时,要严格代入公式求解.
(2)利用平均数的性质求解:若x1, x2, x3,……, xn的平均数为
则ax1+b, ax2+b, ax3+b,…, axn+b的平均数为
方法规律
课堂小结
抽签法
2.最常用的简单随机抽样
随机数法(随机试验、信息技术)
一般地,设一个总体含有N个个体,从中逐个地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,这种抽样方法叫做简单随机抽样.
1.简单随机抽样的概念
3.总体均值与样本均值
在1936年美国总统选举前,一份颇有名气的杂志(Literary Digest)的工作人员做了一次民意测验.调查兰顿(A.Landon)(当时任堪萨斯州州长)和罗斯福(F.D.Roosevelt)(当时的总统)中谁将当选下一届总统,为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发放了调查表。(注意:在1936年电话和汽车只有少数富人有), 通过分析收回的调查表,显示兰顿非常受欢迎,于是此杂志预测兰顿将在选举中获胜.
实际选举结果正好相反,最后罗斯福在选举中获胜,其数据如下:
候选人 预测结果(%) 选举结果(%)
罗斯福 43 62
兰顿 57 38
课外延伸
5
作业:请你查找相关资料,并结合自己的分析,完成一篇调查报告,
报告至少应该包含以下两个方面内容:
1.分析该预测结果出错的原因;2.如何更好的进行选举民意调查.
(第一课时)
9.1.1 简单随机抽样
简单随机抽样定义
一天,妈妈叫儿子去买一盒饼。临出门前嘱咐儿子要买咸口味的饼。儿子拿着钱出门了,过了好一会儿,儿子才回到家。
“都是咸口味的吗?”妈妈问。
“都是咸口味的。”
“你这么肯定?”
儿子递过一盒空的饼盒,兴奋地说:
“我每个都尝过啦。”
— 开心小故事 —
简单随机抽样定义
思考①
在这则笑话中,儿子采用的是什么调查方式?
思考②
思考:你知道我国有哪些数据是普查的吗?
普查:对每一个调查对象都进行调查的方法,称为全面调查。
人口普查,经济普查,农业普查,工业普查
统计学是通过收集数据和分析数据来认识未知现象的一门科学,它可以为人们制定决策提供依据。统计中数据分析的过程如下:
收集数据
整理数据
提取信息
构建模型
进行推断
获得结论
?
两种常用的简单随机抽样方法
3
人口普查流程:
一、准备工作
二、摸底工作
三、登记工作
四、对比复查工作
五、质量控制工作
六、现场验收
2019年11月,经李克强总理签批,国务院印发《关于开展第七次全国人口普查的通知》。根据《中华人民共和国统计法》和《全国人口普查条例》规定,国务院决定于2020年开展第七次全国人口普查。普查标准时点是2020年11月1日零时,彻查人口出生变动情况以及房屋情况。
统计相关概念
1
普查
像人口普查这样,对每一个调查对象都进行调查的方法,称为全面调查,又叫普查.
我们把调查对象的全体称为总体,组成总体的每一个调查对象称为个体.
为了强调调查目的,也可以把调查对象的某些指标的全体作为总体,
每一个调查对象的相应指标作为个体.
例.
在全国人口普查中:
总体:
个体:
全国所有居民.
每一个居民.
/全国所有居民的性别、年龄等.
/每一个居民的性别、年龄等.
思考1.
普查有何优缺点?
优点:数据全面
缺点:花费高、效率低,可能具有破坏性
统计相关概念
1
该调查方式为普查吗?
不是
抽样调查
为什么不进行普查?
统计相关概念
1
抽样调查
根据一定目的,从总体中抽取一部分个体进行调查,并以此为依据对总体的情况作出估计和推断的调查方法,称为抽样调查.
两种基本的抽样方法——
简单随机抽样
从总体中抽取的那部分个体称为样本,
样本中包含的个体数称为样本容量,简称样本量.
调查样本获得的变量值称为样本的观测数据,简称样本数据.
分层随机抽样
花费少,效率高
思考2
抽样调查有何优缺点?
你能举出一些适合用抽样调查的例子吗?
优点:花费少、效率高;缺点:结果与实际情况可能有误差
在一次数学课堂上,陈老师请四位同学列举出生活中运用全面调查或抽样调查的例子.
小凉:为了了解玉米种子的发芽情况,采用抽样调查.
小爽:为了了解全班同学是否给父母洗过脚,采用全面调查.
小夏:为了了解某批导弹的射程,采用全面调查.
小天:为了了解全国中学生安全自救知识的掌握情况,采用抽样调查.
你认为以上四位同学所列举的事例的调查方式错误的是
A.小凉 B.小爽 C.小夏 D.小天
例1
√
下列调查方式,你认为最合适的是
A.了解北京每天的流动人口数,采用抽样调查
B.旅客上飞机前的安检,采用抽样调查
C.了解北京居民“建党百年庆祝大会”期间的出行方式,采用全面调查
D.日光灯管厂要检测一批灯管的使用寿命,采用全面调查
跟踪训练1
√
9.1.1 简单随机抽样
假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同,你能通过抽样调查的方法估计袋中红球所占的比例吗?
放回的摸球
探究.
用摸到红球的频率估计口袋中红球所占的比例。
不放回的摸球
思考3
为什么能用摸到红球的频率估计口袋中红球所占的比例?
每一个小球被摸到的概率相等
简单随机抽样
2
放回摸球的效率高,还是不放回摸球的效率高?
思考4
不放回
简单随机抽样
2
简单随机抽样
一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤n<N)个个体作为样本,如果抽取是放回的,且每次抽取时总体内的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做放回简单随机抽样,如果抽取是不放回的,且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等,我们把这样的抽样方法叫做不放回简单随机抽样.放回简单随机抽样和不放回简单随机抽样统称为简单随机抽样.通过简单随机抽样获得的样本称为简单随机样本.
说明:
1.除非特殊声明,本章所称的简单随机抽样指不放回简单随机抽样.
2.从总体中,逐个不放回地抽取n个个体作为样本和一次性抽取n个个体作为样本,两种方法是等价的.
各个个体被抽到的概率都相等
在简单随机抽样中,某一个个体被抽到的可能性
A.与第几次抽样有关,第一次抽到的可能性大一些
B.与第几次抽样无关,每次抽到的可能性都相等
C.与第几次抽样有关,最后一次抽到的可能性要大些
D.与第几次抽样无关,每次都是等可能地抽取,但各次抽取的可能性不
一定
例2
√
在简单随机抽样中,每一个个体被抽到的可能性都相等,与第几次抽样无关,故A,C,D不正确,B正确.
(2)从总体容量为N的一批零件中,通过简单随机抽样抽取一个容量为30的样本,若每个零件被抽到的可能性为0.25,则N的值为
A.120 B.200 C.150 D.100
√
两种简单随机抽样方法
3
1.抽签法
1.先给712名学生编号,例如按1~712进行编号.
编号
2.然后把所有编号写在外观、质地等无差别的小纸片(也可以是卡片、小球等)上作为号签,并将这些小纸片放在一个不透明的盒里,充分搅拌.最后从盒中不放回地逐个抽取号签.
3.使与号签上的编号对应的学生进入样本,直到抽足样本所需要的人数.
抽签
取样
一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级的平均身高,以便设定可调节课桌椅的标准高度。已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本?
例题
两种简单随机抽样方法
3
一家家具厂要为树人中学高一年级制作课桌椅,他们事先想了解全体高一年级的平均身高,以便设定可调节课桌椅的标准高度。已知树人中学高一年级有712名学生,如果要通过简单随机抽样的方法调查高一年级学生的平均身高,应该怎样抽取样本?
2.随机数法
1.先给712名学生编号,例如按1~712进行编号.
2.用随机数工具产生1~712范围内的整数随机数,把产生的随机数作为抽中的编号.
3.使与编号对应的学生进入样本.重复上述过程,直到抽足样本所需要的人数.
编号
产生随机数
取样
例题
两种简单随机抽样方法
3
思考5
如何生成随机数?
(1) 用随机试验生成随机数
准备10个大小、质地一样的小球,小球上分别写上数字0,1,2,3,…,9,把它们放入一个不透明的袋中.从袋中有放回摸取3次,每次摸取前充分搅拌,并把第一、二、三次摸到的数字分别作为百、十、个位数,这样就生成了一个三位随机数.如果这个三位数在1~712范围内,就代表对应编号的学生被抽中,否则舍弃编号.这样产生的随机数可能会有重复.
如果生成的随机数有重复,即同一编号被多次抽到,可以剔除重复的编号并重新产生随机数,直到产生的不同编号个数等于样本所需要的人数.
如果生成的随机数有重复,该如何解决?
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
①用计算器生成随机数
random随机的
integer
整数
该方法生成的随机数可能重复
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
②用电子表格软件生成随机数
该方法生成的随机数可能重复
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
③用R统计软件生成随机数
样本
不放回
该方法生成的随机数不重复
有放回
该方法生成的随机数可能重复
两种简单随机抽样方法
3
思考5
如何生成随机数?
(2) 用信息技术生成随机数
③用R统计软件生成随机数
除了上述软件以外,还有很多能够产生随机数的软件,
一般的抽签软件,如:抽签助手,抽签器等;
专业的统计软件,如:SAS,SPSS,S-Plus,State等;
综合性较强的数学软件,如:MATLAB,Mathematica,GeoGebra等.
小贴士
样本
不放回
两种简单随机抽样方法
3
抽样方法 优点 缺点
抽签法 简单易行 总体量较大时,
制作号签成本高,
“均匀搅拌”困难.
随机数法 利用信息技术产生随机数方便、快捷、效率高,可节省成本. 随机试验和部分软件可能会产生重复随机数,需要剔除重复编号并重新产生.
思考6
比较随机数法与抽签法,它们各有什么优点和缺点?
为了了解某校高三学生每天的作业量,通过简单随机抽样从该校高三学生中抽取了60名学生,通过调查发现这60名学生每天完成作业平均用时2小时,则可以推测该校高三学生每天完成作业所需时间的平均数
A.一定为2小时 B.高于2小时
C.低于2小时 D.约为2小时
跟踪训练4
√
样本平均数具有随机性,只能估计总体平均数.
两种简单随机抽样方法
3
思考7
用简单随机抽样的方法抽取样本,样本量是否越大越好?
对于样本的代表性,一般说来,样本量大的会好于样本量小的.
从调查的成本角度,样本量大会导致人力、费用、时间等成本的增加.
因此,抽样调查中样本量的选择要根据实际问题的需要,在精度和费用两者间进行权衡,
并不一定是越大越好.
两种简单随机抽样方法
3
练习
教材P177 练习1~4
1.在以下调查中,总体、个体各是什么?哪些适合用全面调查?哪些适合用抽样调查?
(1) 调查一个班级学生每周的体育锻炼时间;
(2) 调查一个地区结核病的发病率;
(3) 调查一批炮弹的杀伤半径;
(4) 调查一个水库所有鱼中草鱼所占的比例.
总体:全班学生,个体:这个班的每一位学生,
适合用全面调查.
总体:整个地区的居民,个体:这个地区的每一位居民,
适合用抽样调查.
总体:这批炮弹,个体:这批炮弹的每一个炮弹,
适合用抽样调查.
总体:这个水库里所有的鱼,个体:这个水库里的每一条鱼,
适合用抽样调查.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
变1.(多选)为了了解全校240名高一学生的身高情况,从中抽取了40名学生进行测量.下列说法正确的是
A.总体是240名学生 B.个体是每一名学生
C.样本是任意40名学生 D.样本容量是40
√
√
√
在这个问题中,总体是240名学生,个体是每一名学生,样本是抽取的40名学生,样本容量是40.
两种简单随机抽样方法
3
练习
教材P177 练习1~4
2.如图,由均匀材质制成的一个正20面体(每个面都是正三角形),将20个平面平分成10组,第1组标上0,第2组标上1,…,第10组标上9.
是;
是.
投掷正20面体,若把朝上一面的数字作为投掷结果,则出现0,1,2,…,9是等可能的吗?
(2) 三个正20面体分别涂上红、黄、蓝三种颜色,分别代表百位、十位、个位,同时投掷可以产生一个三位数(百位为0的也看作三位数),它是000~999范围内的随机数吗?
两种简单随机抽样方法
3
练习
教材P177 练习1~4
3.实验室的笼子里共有100只小白鼠,现要从中抽取10只作试验用.下列两种情况是否属于简单随机抽样?请说明理由.
(1) 每次不经任何挑选地抓一只,抓满10只为止;
(2) 将笼中的100只小白鼠按1~100编号,任意选出编号范围内的10个不重复数字,把相应编号的小白鼠作为试验用的小白鼠.
是,
每次抽取时,没进入样本的各个个体被抽到的概率相同,
不放回简单随机抽样;
是,
该抽样方法类等同于简单随机抽样中的抽签法.
两种简单随机抽样方法
3
练习
教材P177 练习1~4
4.如果计算器只能生成[0,1)内的随机数,你有办法把它转化为1~100范围内的整数随机数吗?转化为1~712范围内的整数随机数呢?
记r为生成的[0,1)内的随机数
则x为1~100范围内的整数随机数;
同理,令y为712r+1的整数部分,则y为1~712范围内的整数随机数.
令x为100r+1的整数部分,
(也可写作x=[100r+1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.从某批零件中抽取50个,然后再从抽取的50个中抽出40个进行合格检查,发现合格品有36个,则可以推测该批产品的合格率为
A.36% B.72% C.90% D.25%
√
问题1 下面是用随机数法从树人中学高一年级学生中抽取的一个容量为50的简单随机样本,他们的身高变量值(单位:cm)如下:
156.0 166.0 157.0 155.0 162.0 168.0 173.0 155.0 157.0 160.0
175.0 177.0 158.0 155.0 161.0 158.0 161.5 166.0 174.0 170.0
162.0 155.0 156.0 158.0 183.0 164.0 173.0 155.5 176.0 171.0
164.5 160.0 149.0 172.0 165.0 176.0 176.0 168.5 171.0 169.0
156.0 171.0 151.0 158.0 156.0 165.0 158.0 175.0 165.0 171.0
试求树人中学高一年级学生的平均身高大约为多少?
探究新知
解:由这些样本观测数据,我们可以计算出样本的平均数为
上面我们通过简单随机抽样得到部分学生的平均身高,并用样本平均身高来估计树人中学高一年级学生的平均身高.
由此可以估计树人中学高一年级学生的平均身高为164.3cm左右.
探究新知
4.总体平均数与样本平均数
(1)总体平均数:
一般地,总体中有N个个体,它们的变量值分别为 Y1,Y2,…,YN,则称 为总体均值,又称总体平均数.
频数
频率
探究新知
4.总体平均数与样本平均数
(1)总体平均数:
一般地,总体中有N个个体,它们的变量值分别为 Y1,Y2,…,YN,则称 为总体均值,又称总体平均数.
总体均值加权平均数的形式:
探究新知
(2)样本平均数:
如果从总体中抽取一个容量为n的样本,它们的变量值分别为 y1,y2,…,yn,则称 为样本均值,又称样本平均数.
样本均值加权平均数的形式:
例题讲解
例5 某公司的人员构成及工资数如下:
经理1人,周工资4000元;高层管理人员3人,周工资均为1000元;高级技工4人,周工资均为900元;工人6人,周工资均为700元;学徒1人,周工资为500元.计算该公司员工周工资的平均数.
探究新知
探究:小明想考察一下简单随机抽样的估计效果, 他从树人中学医务室得到了高一年级学生身高的所有数据, 计算出整个年级学生的平均身高为165.0cm. 然后, 小明用简单随机抽样的方法, 从这些数据中抽取了样本量为50和100的样本各10个, 分别计算出样本平均数, 如下表所示, 从小明多次抽样所得的结果中, 你有什么发现?
抽样序号 1 2 3 4 5 6 7 8 9 10
样本量为50的平均数 165.2 162.8 164.4 164.4 165.6 164.8 165.3 164.7 165.7 165.0
样本量为100的平均数 164.4 165.0 164.7 164.9 164.6 164.9 165.1 165.2 165.1 165.2
为了更方便地观察数据,以便我们分析样本平均数的特点以及与总体平均数的关系,我们把这20次试验的平均数用图形表示出来,如右图所示. 图中的红线表示树人中学高一年级全体学生身高的平均数.
探究新知
总体平均数是总体的一项重要特征. 另外,某类个体在总体中所占的比例也是人们关心的一项总体特征,例如全部产品中合格品所占的比例、赞成某项政策的人在整个人群中所占的比例等.
从试验结果看,不管样本量为50,还是为100,不同样本的平均数往往是不同的. 由于样本的选取是随机的,因此样本平均数也具有随机性,这与总体平均数是一个确定的数不同.
虽然在所有20个样本平均数中,与总体平均数完全一致的很少,但除了样本量为50的第2个样本外,样本平均数偏离总体平均数都不超过1cm,
即大部分样本平均数离总体平均数不远,在总体平均数附近波动.
比较样本量为50和样本量为100的样本平均数,还可以发现样本量为100的波动幅度明显小于样本量为50的,这与我们对增加样本量可以提高估计效果的认识是一致的.
探究新知
问题2 眼睛是心灵的窗户,保护好视力非常重要. 树人中学在“全国爱眼日”前,想通过简单随机抽样的方法,了解一下全校2174名学生中视力不低于5.0的学生所占的比例,你觉得该怎样做?总体、个体、变量分别是什么?
全体学生构成调查的总体,每一位学生是个体,学生的视力是考察的变量.
为了便于问题的描述,我们记“视力不低于5.0”为1,“视力低于5.0”为0,则第i个(i=1,2,...,2174)学生的视力变量值为
探究新知
例如,现在,我们从树人中学所有学生中抽取一个容量为50的简单随机样本,其视力变量取值如下:1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 1 1 1 0 1 1 0 1 1
1 1 0 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 0 0
由样本平均数,我们估计在树人中学全体学生中,“视力不低于5.0”的比例约为0.54.
探究新知
简单随机抽样的优缺点:
在实际应用中,简单随机抽样有一定局限性.
例如,当总体很大时,编号等准备工作耗费时间、人工,甚至难以做到;抽中个体较为分散,要找到样本中的个体进行调查会遇到很多困难;简单随机抽样没有其他辅助信息,估计效率不是很高.
简单随机抽样方法简单、直观,用样本平均数估计总体平均数也比较方便. 简单随机抽样是一种基本抽样方法,是其他抽样方法的基础.
因此,在规模较大的调查中,直接采用简单随机抽样的并不多,一般是把简单随机抽样和其他抽样方法组合使用.
优点:
缺点:
课堂练习
(1)计算芳芳上学期平时的平均成绩;(2)如果学期的总评成绩按右图所示的比例计算,请计算出芳芳该学期的总评成绩.
1.芳芳在九年级上学期的数学成绩如下表所示:
答:芳芳上学期平时的平均成绩是86分.
(2)86×10%+90×30%+85×60%=86.6.
答:芳芳该学期的总评成绩是86.6分.
测验类别 平时 期中考试 期末考试
测验1 测验2 测验3 测验4 成绩 88 72 98 86 90 85
2.已知一组数据x1, x2, x3, x4, x5的平均数是2,那么另一组数据2x1-1,2x2-1,2x3-1,2x4-1,2x5-1的平均数为________.
课堂练习
3
解析:因为数据x1, x2, x3, x4, x5的平均数是2,所以
所以数据2x1-1, 2x2-1,2x3-1,2x4-1,2x5-1的平均数为
探究新知
平均数的求解方法
(1)利用公式求解:平均数反映了一组数据的整体水平,平均数的大小与一组数据中每个数据均有联系,任何一个数据的变动都会相应引起平均数的变动. 所以求平均数时,要严格代入公式求解.
(2)利用平均数的性质求解:若x1, x2, x3,……, xn的平均数为
则ax1+b, ax2+b, ax3+b,…, axn+b的平均数为
方法规律
课堂小结
抽签法
2.最常用的简单随机抽样
随机数法(随机试验、信息技术)
一般地,设一个总体含有N个个体,从中逐个地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,这种抽样方法叫做简单随机抽样.
1.简单随机抽样的概念
3.总体均值与样本均值
在1936年美国总统选举前,一份颇有名气的杂志(Literary Digest)的工作人员做了一次民意测验.调查兰顿(A.Landon)(当时任堪萨斯州州长)和罗斯福(F.D.Roosevelt)(当时的总统)中谁将当选下一届总统,为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发放了调查表。(注意:在1936年电话和汽车只有少数富人有), 通过分析收回的调查表,显示兰顿非常受欢迎,于是此杂志预测兰顿将在选举中获胜.
实际选举结果正好相反,最后罗斯福在选举中获胜,其数据如下:
候选人 预测结果(%) 选举结果(%)
罗斯福 43 62
兰顿 57 38
课外延伸
5
作业:请你查找相关资料,并结合自己的分析,完成一篇调查报告,
报告至少应该包含以下两个方面内容:
1.分析该预测结果出错的原因;2.如何更好的进行选举民意调查.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
