4.2.2 指数函数的图象及性质 课件(共23张PPT)
文档属性
| 名称 | 4.2.2 指数函数的图象及性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 09:47:30 | ||
图片预览



文档简介
(共23张PPT)
4.2 指数函数
4.2.1 指数函数的图象及性质
指数函数的概念
一般地,形如 的函数叫做指数函数,其中 是自变量,函数的定义域是_____.
复 习
1.用列表,描点法画出指数函数图象,能从数形两方面认识指数函数的性质;
2.通过观察、总结指数函数的图像与性质;掌握底数对指数函数图象的影响;
3.学会利用指数函数单调性来比较大小;
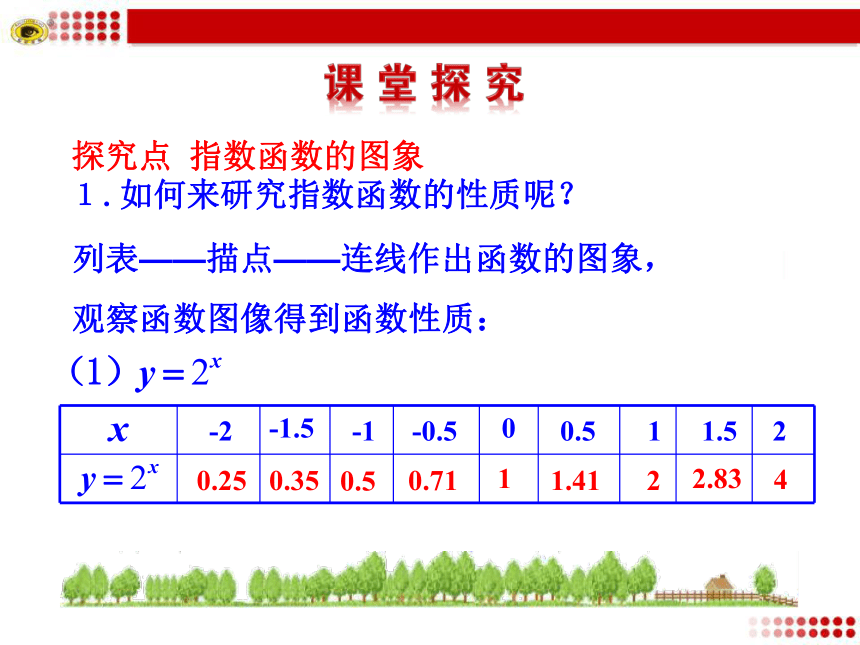
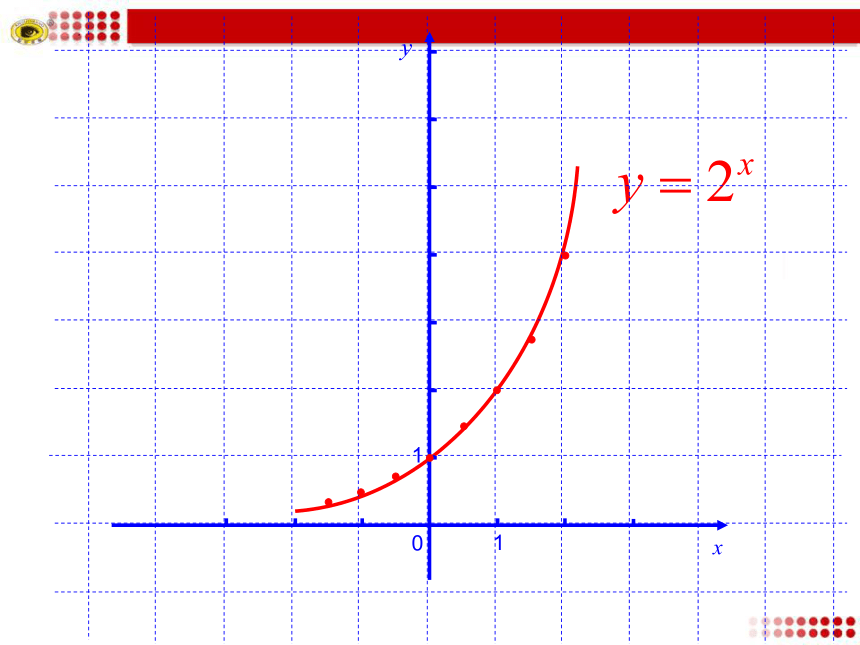
列表——描点——连线作出函数的图象,
观察函数图像得到函数性质:
1.如何来研究指数函数的性质呢?
探究点 指数函数的图象
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0.5
0.25
0.35
0.71
1
1.41
2
2.83
4
0
1
1
0
1
1
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
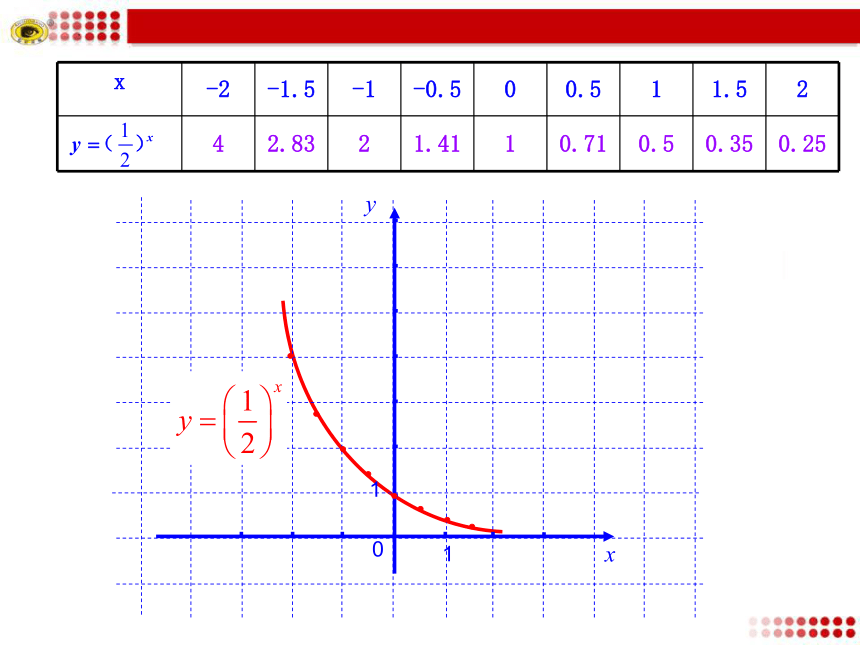
4 2.83 2 1.41 1 0.71 0.5 0.35 0.25
0
1
1
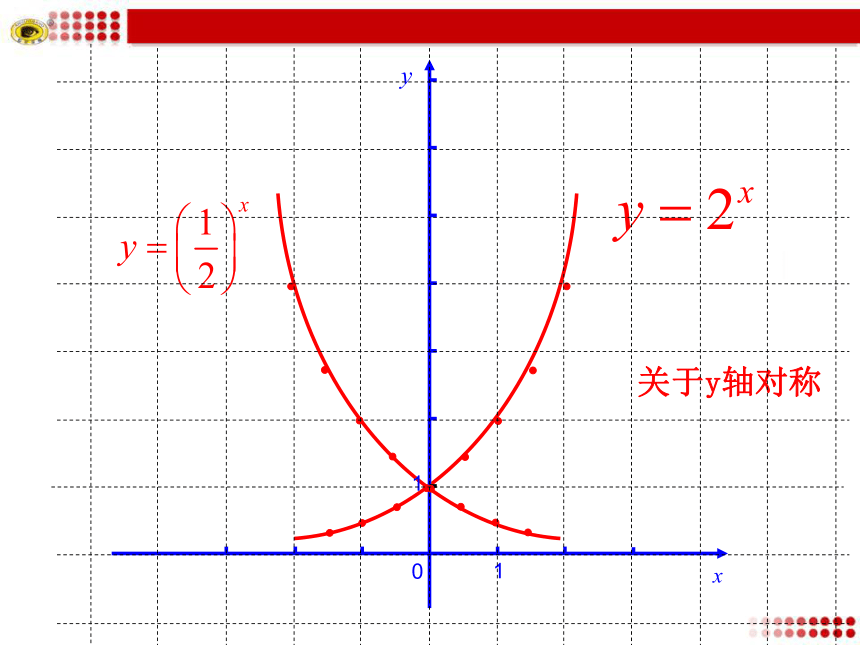
关于y轴对称
…
0.037
0.11
0.33
1
3
9
27
…
y=3-x
…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
3
2
1
0
-1
-2
-3
…
x
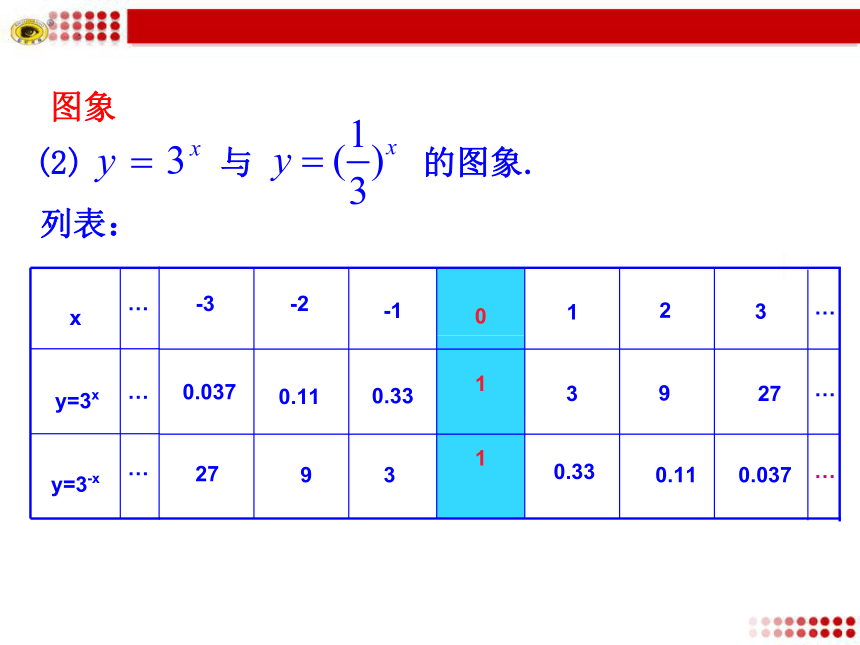
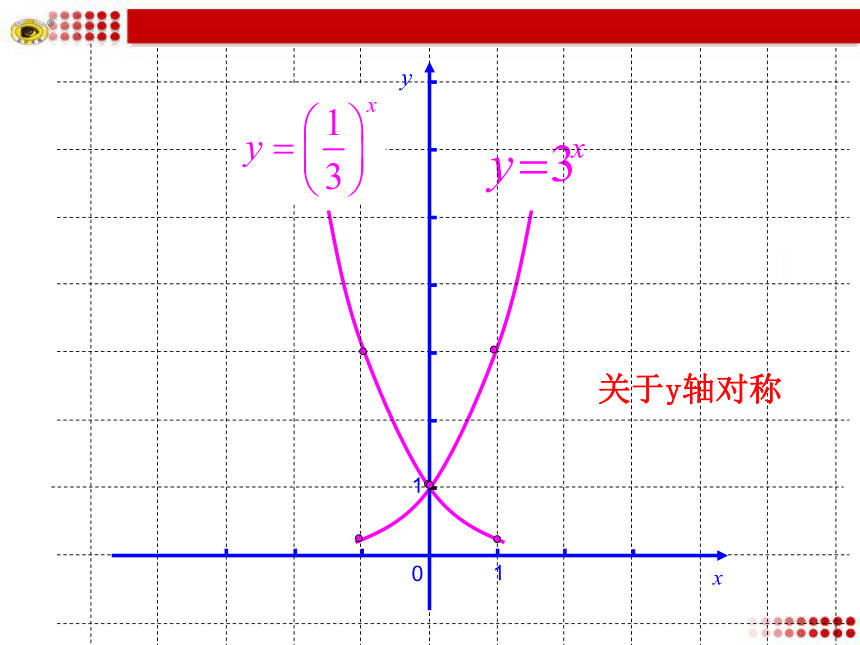
(2) 与 的图象.
列表:
图象
0
1
1
关于y轴对称
0
1
1
小结:底数互为倒数的指数函数的图象关于y轴对称
0
1
1
0
1
1
0
1
0
1
y=ax (0y=ax (a>1)
0
1
0
1
图象共同特征:
(1)图象可向左、右两方无限伸展
(3)都经过坐标为(0,1)的点
(2)图象都在x轴上方
图象在R上单调递增
图象在R上单调递减
(2)在R上是减函数
(1)过定点(0,1),即x=0时,y=1
性质
(0,+∞)
值域
R
定义
域
图象
a>1
0探究点 指数函数的性质
(2)在R上是增函数
0
1
0
1
例1.比较下列各题中两个值的大小
解:(1)根据函数y=1.7x的性质:y=1.7x在R上单调递增,∵2.5<3 ∴1.72.5<1.73。
(2)根据函数y=0.8x的性质:y=0.8x在R上单调递减,∵-0.1>-0.2 ∴0.8-0.1<0.8-0.2。
(3)根据函数y=1.7x的性质,1.70.3>1.70=1,
根据函数y=0.9x的性质,0.93.1<0.90=1,
所以1.70.3>0.93.1
根据指数函数的性质
用“>”或“<”填空:
>
>
<
<
【变式练习】
1.函数y=ax-3+2(a>0且a≠1)的图象一定经过点
P,则P点的坐标为( )
A.(-2,-3) B.(3,3)
C.(3,2) D.(-3,-2)
【解析】因为y=ax-3+2(a>0且a≠1),
所以当x-3=0,即x=3时,y=3,
所以函数y=ax-3+2(a>0且a≠1)的图象过定点
P(3,3).
【解析】c,d大于1
且c>d
a,b大于0小于1
且b<a
∴b<a<1<d<c
结论:在第一象限,离x轴越远底数越大
2.如图,指数函数:A. y=ax B.y=bx C.y=cx D. y=dx
的图象,则a,b,c,d与1的大小关系是________________.
x
y
B
D
C
A
O
b<a<1<d<c
3.如图的曲线是C1、C2、C3、C4是指数函数 的
图象,而 ,则图象C1、C2、C3、C4
对应的函数图象的底数依次是________________
解析:在第一象限,图象离x轴越远
底数越大。
4.若0∴
∵
∴
解:根据函数 的性质:
∵ , ∴ 在R上单调递减
∴不等式的解集为
5.若 ,求x的取值范围.
解:根据函数 的性质:
(1)当 时, 在R上单调递减,
∵
∴
∴
(2)当 时, 在R上单调递增,
∵
∴
∴
综上所述:当 时,x的取值范围为
当 时, x的取值范围为
一般地,函数y=ax(a>0,且a≠1)叫做指数函数.
1.指数函数的定义
2.指数函数的图象和性质
底数
图象
定义域
R
值域
性质
(1)过定点(0,1),即x=0时,y=1
(2)在R上是减函数 (2)在R上是增函数
水若长流能成河,山因积石方为高
4.2 指数函数
4.2.1 指数函数的图象及性质
指数函数的概念
一般地,形如 的函数叫做指数函数,其中 是自变量,函数的定义域是_____.
复 习
1.用列表,描点法画出指数函数图象,能从数形两方面认识指数函数的性质;
2.通过观察、总结指数函数的图像与性质;掌握底数对指数函数图象的影响;
3.学会利用指数函数单调性来比较大小;
列表——描点——连线作出函数的图象,
观察函数图像得到函数性质:
1.如何来研究指数函数的性质呢?
探究点 指数函数的图象
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0.5
0.25
0.35
0.71
1
1.41
2
2.83
4
0
1
1
0
1
1
x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
4 2.83 2 1.41 1 0.71 0.5 0.35 0.25
0
1
1
关于y轴对称
…
0.037
0.11
0.33
1
3
9
27
…
y=3-x
…
27
9
3
1
0.33
0.11
0.037
…
y=3x
…
3
2
1
0
-1
-2
-3
…
x
(2) 与 的图象.
列表:
图象
0
1
1
关于y轴对称
0
1
1
小结:底数互为倒数的指数函数的图象关于y轴对称
0
1
1
0
1
1
0
1
0
1
y=ax (0
0
1
0
1
图象共同特征:
(1)图象可向左、右两方无限伸展
(3)都经过坐标为(0,1)的点
(2)图象都在x轴上方
图象在R上单调递增
图象在R上单调递减
(2)在R上是减函数
(1)过定点(0,1),即x=0时,y=1
性质
(0,+∞)
值域
R
定义
域
图象
a>1
0
(2)在R上是增函数
0
1
0
1
例1.比较下列各题中两个值的大小
解:(1)根据函数y=1.7x的性质:y=1.7x在R上单调递增,∵2.5<3 ∴1.72.5<1.73。
(2)根据函数y=0.8x的性质:y=0.8x在R上单调递减,∵-0.1>-0.2 ∴0.8-0.1<0.8-0.2。
(3)根据函数y=1.7x的性质,1.70.3>1.70=1,
根据函数y=0.9x的性质,0.93.1<0.90=1,
所以1.70.3>0.93.1
根据指数函数的性质
用“>”或“<”填空:
>
>
<
<
【变式练习】
1.函数y=ax-3+2(a>0且a≠1)的图象一定经过点
P,则P点的坐标为( )
A.(-2,-3) B.(3,3)
C.(3,2) D.(-3,-2)
【解析】因为y=ax-3+2(a>0且a≠1),
所以当x-3=0,即x=3时,y=3,
所以函数y=ax-3+2(a>0且a≠1)的图象过定点
P(3,3).
【解析】c,d大于1
且c>d
a,b大于0小于1
且b<a
∴b<a<1<d<c
结论:在第一象限,离x轴越远底数越大
2.如图,指数函数:A. y=ax B.y=bx C.y=cx D. y=dx
的图象,则a,b,c,d与1的大小关系是________________.
x
y
B
D
C
A
O
b<a<1<d<c
3.如图的曲线是C1、C2、C3、C4是指数函数 的
图象,而 ,则图象C1、C2、C3、C4
对应的函数图象的底数依次是________________
解析:在第一象限,图象离x轴越远
底数越大。
4.若0
∵
∴
解:根据函数 的性质:
∵ , ∴ 在R上单调递减
∴不等式的解集为
5.若 ,求x的取值范围.
解:根据函数 的性质:
(1)当 时, 在R上单调递减,
∵
∴
∴
(2)当 时, 在R上单调递增,
∵
∴
∴
综上所述:当 时,x的取值范围为
当 时, x的取值范围为
一般地,函数y=ax(a>0,且a≠1)叫做指数函数.
1.指数函数的定义
2.指数函数的图象和性质
底数
图象
定义域
R
值域
性质
(1)过定点(0,1),即x=0时,y=1
(2)在R上是减函数 (2)在R上是增函数
水若长流能成河,山因积石方为高
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
