18.1.2 平行四边形的判定 教案 课时 2(含答案)
文档属性
| 名称 | 18.1.2 平行四边形的判定 教案 课时 2(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 444.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 22:59:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章《平行四边形》教案
18.1.2平行四边形的判定
第2课时
教学目标:
理解并掌握三角形中位线的概念及性质,并能熟练地应用三角形中位线的性质进行有关的证明和计算.
重点:
运用三角形中位线的性质解决问题.
难点:
三角形中位线性质的证明.
教学流程:
一、导入新课
想一想:平行四边形的相关知识?
答案:围绕思维导图进行回顾
.
导言:我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质研究平行四边形的有关问题,下面我们利用平行四边形研究三角形的有关问题.
二、新课讲解
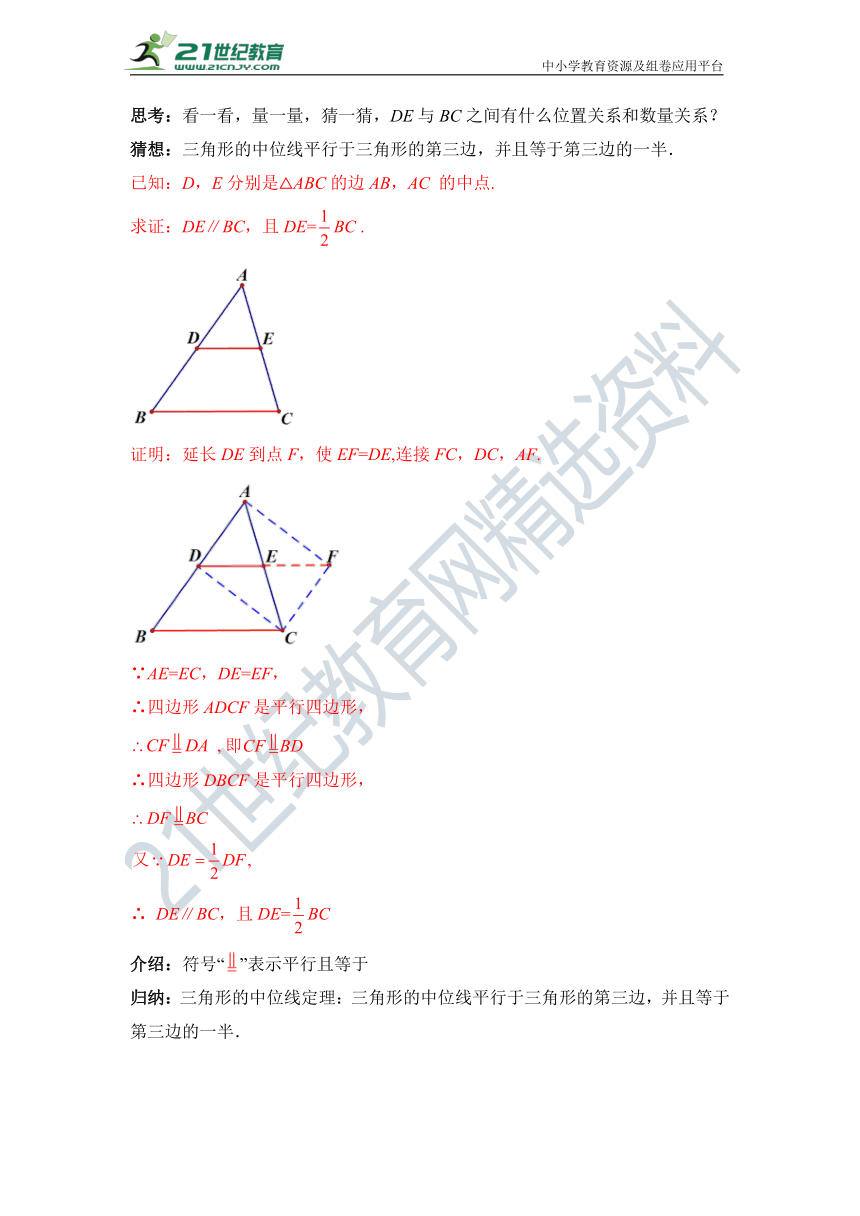
观察:如图,△ABC中,D,E分别是边AB,AC 的中点,连接DE.
指出:连接三角形两边中点的线段叫做三角形的中位线.
思考:看一看,量一量,猜一猜,DE与BC之间有什么位置关系和数量关系?
猜想:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:D,E分别是△ABC的边AB,AC 的中点.
求证:DE∥BC,且DE=BC .
证明:延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,
∴四边形DBCF是平行四边形,
∴ DE∥BC,且DE=BC
介绍:符号“”表示平行且等于
归纳:三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
符号语言:
在△ABC中,
∵D,E分别是边AB,AC的中点,
∴DE∥BC,且DE=BC .
例1:如图,在△ABC中,∠C=90°,AC=8,CB=6,D,E,F分别是BC,AC,AB的中点,则Rt△ABC的中位线分别是___________;四边形AEDF的周长为________.
答案:DE,DF,18
例2:在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接BD,
∵点E,F, G,H分别是边AB、BC、CD、DA的中点。
∴EH为△ABD的中位线,
∴EH∥BD, EH=BD.
同理:FG∥BD, FG=BD,
∴EH∥FG,EH=FG
∴四边形EFGH是平行四边形。
例3:如图,A, B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A, B两点间的距离 根据是什么
解:取AC的中点E,BC的中点F,连接EF,量得EF的长,则A, B两点间的距离可求出,
理由如下:
∵E,F分别是AC,BC的中点,
∴EF是△ABC的中位线,
∴AB=2EF,
设EF=a,则AB=2a.
三、巩固提升
1.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
答案:C
2.如图,为测量池塘边A,B两点间的距离,小明在池塘的一侧选取一点O,测得OA,OB的中点分别是点D,E,且DE=14米,则A,B间的距离是( )
A.30米 B.28米 C.26米 D.24米
答案:B
3.如图,点D,E,F分别是△ABC各边的中点,连接DE,EF,DF.若△ABC的周长为30,则△DEF的周长为________.
答案:15
4.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不变
D.线段EF的长与点P的位置有关
答案:C
5.如图,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接BD,
∵E,H分别是AB,AD的中点,
∴EH是△ABD的中位线,
∴EH=BD,EH∥BD,
同理可证FG=BD,FG∥BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
四、课堂小结
今天我们学习了哪些知识?
1.什么是三角形的中位线?
2.说一说三角形 中位线定理的内容?
五、布置作业
教材P50页习题18.1第5题.
第18章《平行四边形》教案
18.1.2平行四边形的判定
第2课时
教学目标:
理解并掌握三角形中位线的概念及性质,并能熟练地应用三角形中位线的性质进行有关的证明和计算.
重点:
运用三角形中位线的性质解决问题.
难点:
三角形中位线性质的证明.
教学流程:
一、导入新课
想一想:平行四边形的相关知识?
答案:围绕思维导图进行回顾
.
导言:我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质研究平行四边形的有关问题,下面我们利用平行四边形研究三角形的有关问题.
二、新课讲解
观察:如图,△ABC中,D,E分别是边AB,AC 的中点,连接DE.
指出:连接三角形两边中点的线段叫做三角形的中位线.
思考:看一看,量一量,猜一猜,DE与BC之间有什么位置关系和数量关系?
猜想:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:D,E分别是△ABC的边AB,AC 的中点.
求证:DE∥BC,且DE=BC .
证明:延长DE到点F,使EF=DE,连接FC,DC,AF.
∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,
∴四边形DBCF是平行四边形,
∴ DE∥BC,且DE=BC
介绍:符号“”表示平行且等于
归纳:三角形的中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
符号语言:
在△ABC中,
∵D,E分别是边AB,AC的中点,
∴DE∥BC,且DE=BC .
例1:如图,在△ABC中,∠C=90°,AC=8,CB=6,D,E,F分别是BC,AC,AB的中点,则Rt△ABC的中位线分别是___________;四边形AEDF的周长为________.
答案:DE,DF,18
例2:在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接BD,
∵点E,F, G,H分别是边AB、BC、CD、DA的中点。
∴EH为△ABD的中位线,
∴EH∥BD, EH=BD.
同理:FG∥BD, FG=BD,
∴EH∥FG,EH=FG
∴四边形EFGH是平行四边形。
例3:如图,A, B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A, B两点间的距离 根据是什么
解:取AC的中点E,BC的中点F,连接EF,量得EF的长,则A, B两点间的距离可求出,
理由如下:
∵E,F分别是AC,BC的中点,
∴EF是△ABC的中位线,
∴AB=2EF,
设EF=a,则AB=2a.
三、巩固提升
1.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
答案:C
2.如图,为测量池塘边A,B两点间的距离,小明在池塘的一侧选取一点O,测得OA,OB的中点分别是点D,E,且DE=14米,则A,B间的距离是( )
A.30米 B.28米 C.26米 D.24米
答案:B
3.如图,点D,E,F分别是△ABC各边的中点,连接DE,EF,DF.若△ABC的周长为30,则△DEF的周长为________.
答案:15
4.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减小
C.线段EF的长不变
D.线段EF的长与点P的位置有关
答案:C
5.如图,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接BD,
∵E,H分别是AB,AD的中点,
∴EH是△ABD的中位线,
∴EH=BD,EH∥BD,
同理可证FG=BD,FG∥BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
四、课堂小结
今天我们学习了哪些知识?
1.什么是三角形的中位线?
2.说一说三角形 中位线定理的内容?
五、布置作业
教材P50页习题18.1第5题.
