三角形性质应用 1[下学期]

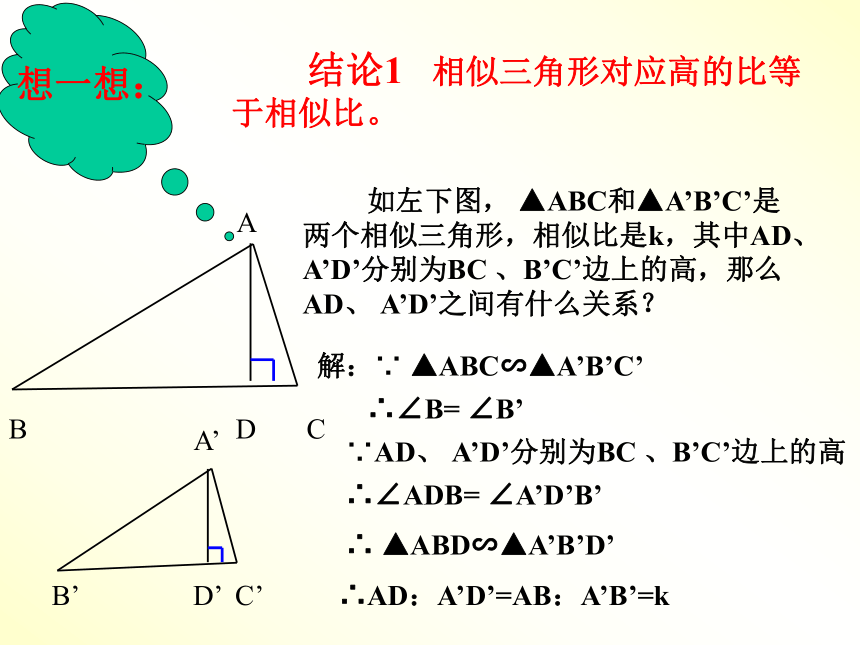
课件23张PPT。相似三角形的性质初二备课组1、相似三角形有那些性质？2、相似三角形有哪些判定 方式？对应线段成比例，对应角相等。⑴ 定义判定1 两角分别对应相等的两三角形相似。⑶ 判定2 两边分别对应成比例，并且夹角相等的两个三角形相似。⑷ 判定3 三边对应成比例的两个三角形相似。？？想一想： 如左下图， ▲ABC和▲A’B’C’是两个相似三角形，相似比是k，其中AD、 A’D’分别为BC 、B’C’边上的高，那么AD、 A’D’之间有什么关系？解：∵ ▲ABC∽▲A’B’C’∴∠B= ∠B’∵AD、 A’D’分别为BC 、B’C’边上的高∴∠ADB= ∠A’D’B’ ∴ ▲ABD∽▲A’B’D’∴AD：A’D’=AB：A’B’=k 结论1 相似三角形对应高的比等于相似比。试一试：
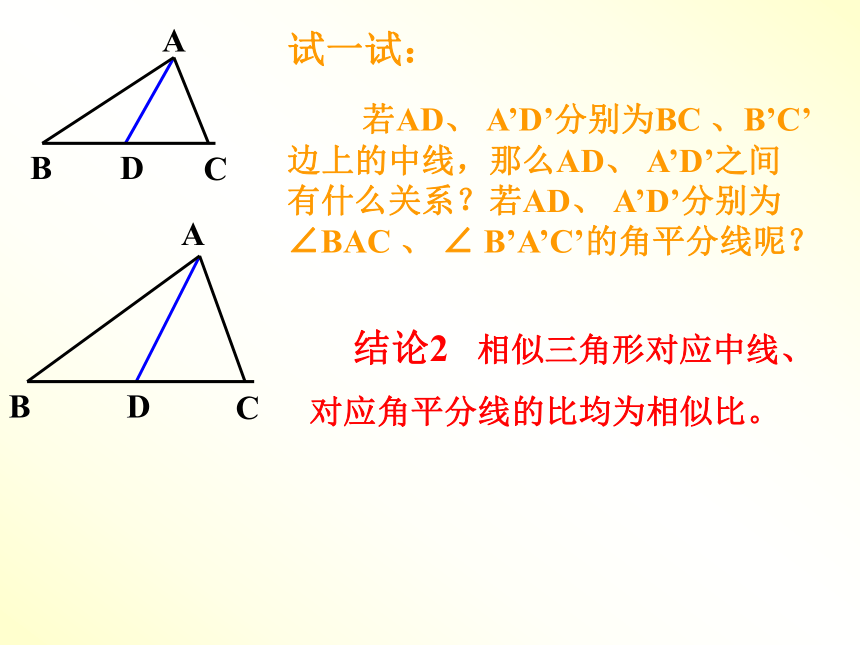
若AD、 A’D’分别为BC 、B’C’边上的中线，那么AD、 A’D’之间有什么关系？若AD、 A’D’分别为∠BAC 、 ∠ B’A’C’的角平分线呢？
结论2 相似三角形对应中线、
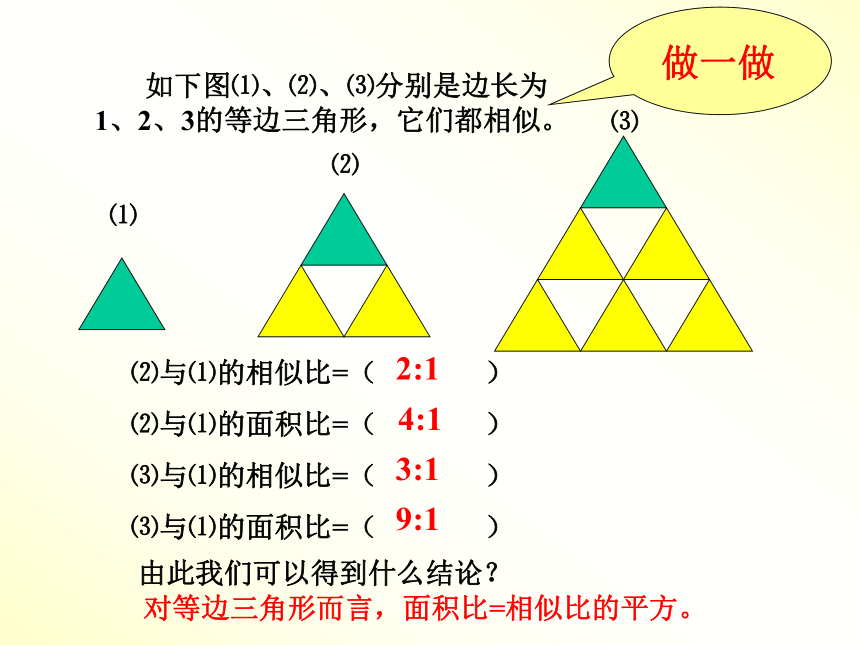
对应角平分线的比均为相似比。做一做 如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形，它们都相似。⑵与⑴的相似比=（ ）
⑵与⑴的面积比=（ ）
⑶与⑴的相似比=（ ）
⑶与⑴的面积比=（ ） 由此我们可以得到什么结论？ 对等边三角形而言，面积比=相似比的平方。2:14:13:19:1 动动你聪明的
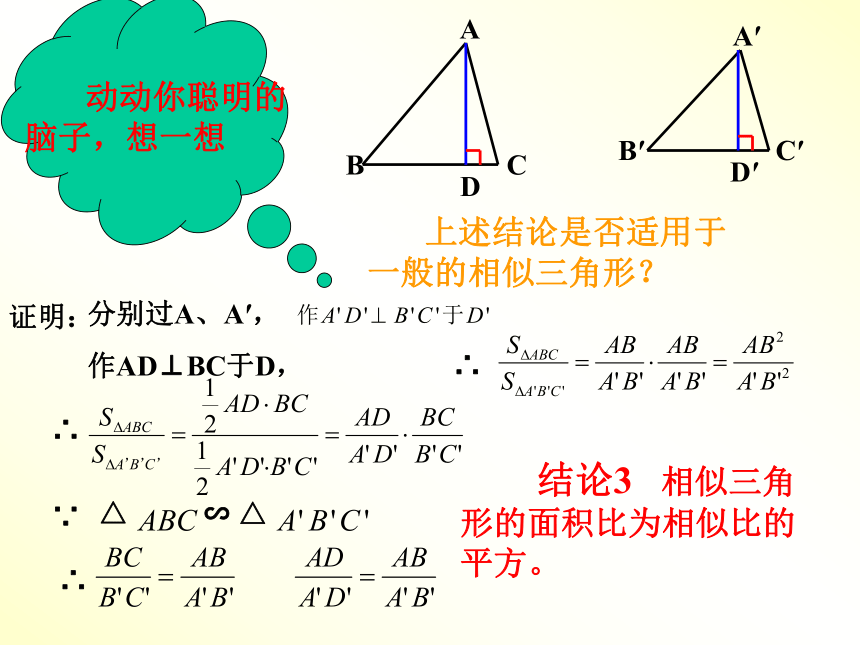
脑子，想一想
上述结论是否适用于一般的相似三角形？DD′证明：分别过A、A′，
作AD⊥BC于D，∵∴∴∴ 结论3 相似三角形的面积比为相似比的平方。相似多边形的面积也有同样的结论吗？想一想（可以以相似四边形为例说明）？两个相似三角形的周长比是多少？结论4 相似三角形的周长比就是相似比。请回答 1、若两个三角形的相似比为3：5，则这两个三角形对应高的比为（ ），对应角平分线的比为( ），周长之比为（ ），对应中线之比为（ ）。 2、把一个三角形改成和它相似的三角形，如果面积扩大为原来的100倍，那么边长扩大为原来的几倍？ 3、已知两个等边三角形的边长之比为2：3，且它们的面积之和为26cm2，则较小的等边三角形的面积为多少？3：53：53：510倍8cm23：5 1、如图，△ABC中，点D、E、F分别在边AB、AC、BC上，DE∥BC，EF∥AB，AE∕EC＝2∕3，S △ABC=S，求S□BFED。例题：求：BC、AC、 、 例2：如图所示，D、E分别是AC、AB上的点，已知△ABC的面积为　　　，　　　　求四边形BCDE的面积。AEBDC展示风采：1、连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.1:21:43.如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
4、如图，点D、E分别是△ABC边AB、AC上的点，且DE∥BC，BD＝2AD，那么△ADE的周长︰△ABC的周长＝　　　　。 6、如图在 ABCD中，E是BC的中点，F是BE的中点，AE与DF交于点H，过点H作MN⊥AD，垂足为M，
交BC于N，则NH:MH=______。 1:43、存在探索型 如图, DE是Rt△ABC的中位线，AF平行于BC，在射线AF上是否存在点M，使△MEC与△ADE相似,若存在,请先确定点 M,再证明这两个三角形相似，若不存在，请说明理由.证明：连结MC，　　　　　　　　　　　∵DE是△ABC的中位线，　　　　　∴DE∥BC，AE＝EC，　　　　　　又∵ME⊥AC, 　　　　　　　　　　∴AM＝CM，　　　　　　　　　　　∴ ∠1= ∠2 ，　　　　　　　　　　　∵∠B=90°，　　　　　　　　　　　∴ ∠4＝ ∠B= 90°，　　　　 　　　　∵AF ∥BC，AM ∥DE, 　　　　　　∴ ∠1= ∠2 ，　　　　　　　　　　　∴ ∠3= ∠2 ,　　　　　　　　　　　∵ ∠ADE＝ ∠MEC=90 ° ， 　　∴ △ADE ∽△MEC．123M解:存在.过点E作AC的垂线,与AF交于一点,即M点(或作∠MCA= ∠AED).4小结 这节课我们学习了相似三角形的一些重要性质： 1、相似三角形对应高、相似三角形对应中线、相似三角形对应角平分线的比等于相似比。 2、相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方。谢谢课外练习题：1 ．已知，在梯形ABCD中，AD∥BC，
点E、F分别在AB、AC上，EF∥BC,EF交AC于G，
若EB=DF，AE=9，CF=4。
求：BE、CD和的值。
2．如图，平行四边形ABCD中，E是CB延长线上一点，
DE交AB于F。
求证：AD·AB＝AF·CE
3．如图，已知矩形ABCD的对角线AC、BD相交于O，
OF⊥AC于O，交AB于E，交CB的延长线于F。
求证：OB是OE与OF的比例中项。