2022-2023学年华东师大版八年级数学下册期末综合复习《第17章函数及其图象》(含答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学下册期末综合复习《第17章函数及其图象》(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 326.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-20 14:24:50 | ||
图片预览



文档简介
2022-2023学年华东师大版八年级数学下册《第17章函数及其图象》
期末综合复习训练题(附答案)
一、单选题
1.下列曲线中不能表示y是x的函数的是( )
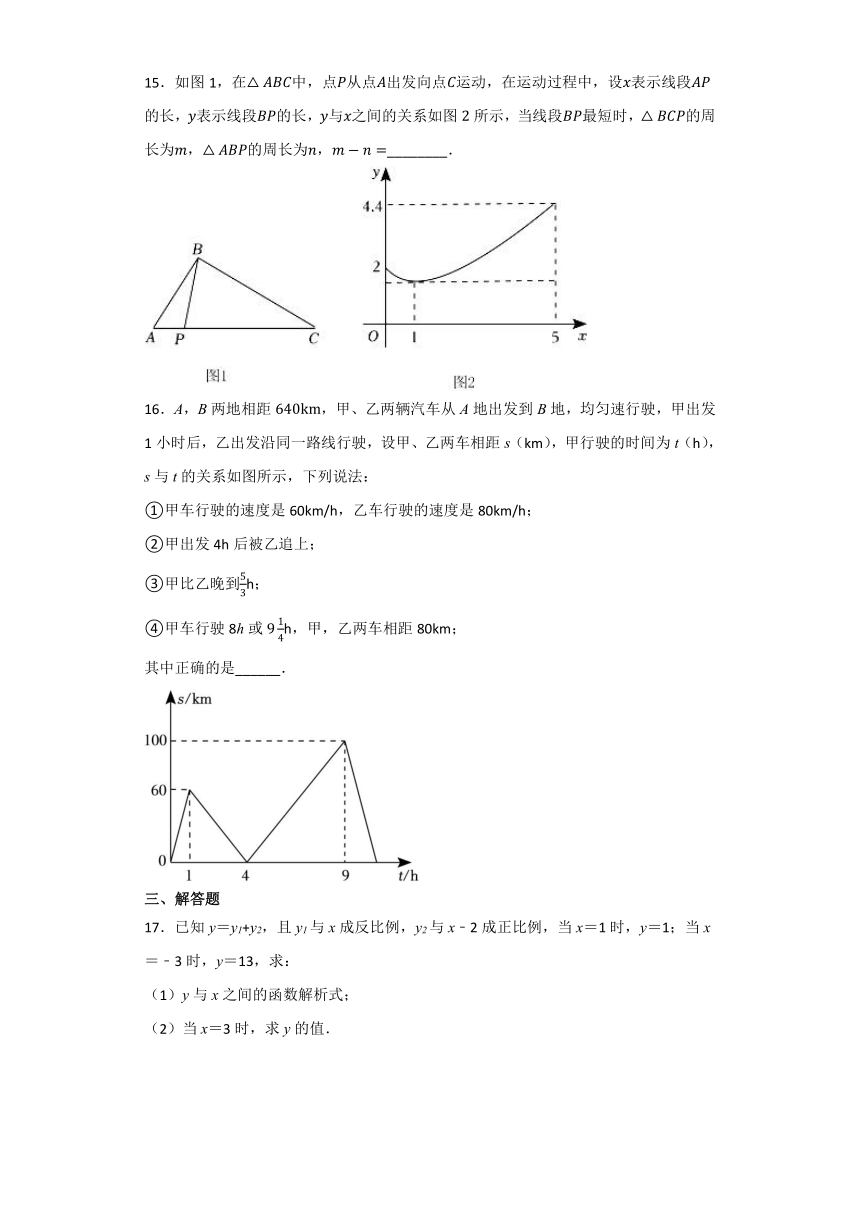
A.B.C.D.
2.若点在第二象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.关于反比例函数的图象,下列说法正确的是( )
A.图象经过点 B.图象分布在第二、四象限
C.两个分支关于x轴成轴对称 D.当时,y随x的增大而增大
4.油箱中存油升,油从油箱中均匀流出,流速为升/分钟,剩余油量(升)与流出时间t(分钟)的函数关系是( )
A. B. C. D.
5.两条直线,关于轴对称,经过点,经过点,则这两条直线,的交点坐标为( )
A. B. C. D.
6.某游客为爬上千米高的山顶看日出,先用小时爬了千米休息小时后,用小时爬上山顶.游客爬山所用时间与山高间的函数关系用图形表示是( )
A. B. C. D.
7.如图,双曲线与直线相交于、两点,点坐标为,则点坐标为( )
A. B. C. D.
8.已知一次函数和的图像都经过点,且与y轴交于点,为坐标系原点,那么的面积是( )
A. B. C. D.
二、填空题
9.某市居民用电价格是元/(千瓦·时),居民应付电费为元,用电量为千瓦·时,其中常量是 ________,变量是 ______________.
10.若点B的坐标为,轴,且,则点A的坐标为________.
11.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t(小时)之间的函数关系式的是________.
12.如图,一次函数(,k,b为常数)的图象与x轴交于点,则关于x的不等式的解集是___.
13.如图,Rt△BOC的一条直角边在x轴正半轴上,双曲线过的斜边的中点,与另一直角边相交于点,若的面积是6,则k的值是_______.
14.一艘轮船和一艘快艇沿相同路线从甲港出发匀速行驶至乙港,行驶路程随时间变化的图象如图,则快艇比轮船每小时多行_____千米.
15.如图1,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示线段的长,与之间的关系如图所示,当线段最短时,的周长为,的周长为,________.
16.A,B两地相距,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到h;
④甲车行驶8h或h,甲,乙两车相距80km;
其中正确的是______.
三、解答题
17.已知y=y1+y2,且y1与x成反比例,y2与x﹣2成正比例,当x=1时,y=1;当x=﹣3时,y=13,求:
(1)y与x之间的函数解析式;
(2)当x=3时,求y的值.
18.如图,甲,乙两名短跑运动员在一次100米赛跑中的路程(m)与时间(s)的关系图象,则:
(1)甲,乙两人中先到达终点的是 ;
(2)乙在这次赛跑中的速度为 m/s.
(3)当先到达终点运动员冲线瞬间,另外一名运动员与他的距离是 米.
19.灞河元朔大桥其设计理念以“千古一舟”为题,象征“舟行古今、跨越时代”的文化内涵,融合西安市花石榴花造型,与奥体中心建筑造型遥相呼应.某天晓玲和小华在元朔大桥上散步,晓玲从大桥上的点A走向点B,同时小华从点B走向点A,晓玲、小华距A点的路程y(米)与行走时间x(分钟)之间的关系如图所示,请结合图象回答下列问题:
(1)晓玲从点A走向点B用了______分钟;
(2)求小华距A点的路程y(米)与行走时间x(分钟)之间的关系式;
(3)求晓玲与小华相遇时距点A的路程.
20.用橡胶或聚脂薄膜材斜制成气球,并充以比空气密度小的氢气或氦气,用以携带仪器升空,进行高空气象观测.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压与气体体积成反比例函数,其图象如图所示.
(1)求这个函数的表达式.
(2)当气体体积为时,气压是多少?
(3)当气球内的气压大于时,气球将煤炸,为了安全起见,气体的体积应不小于多少?
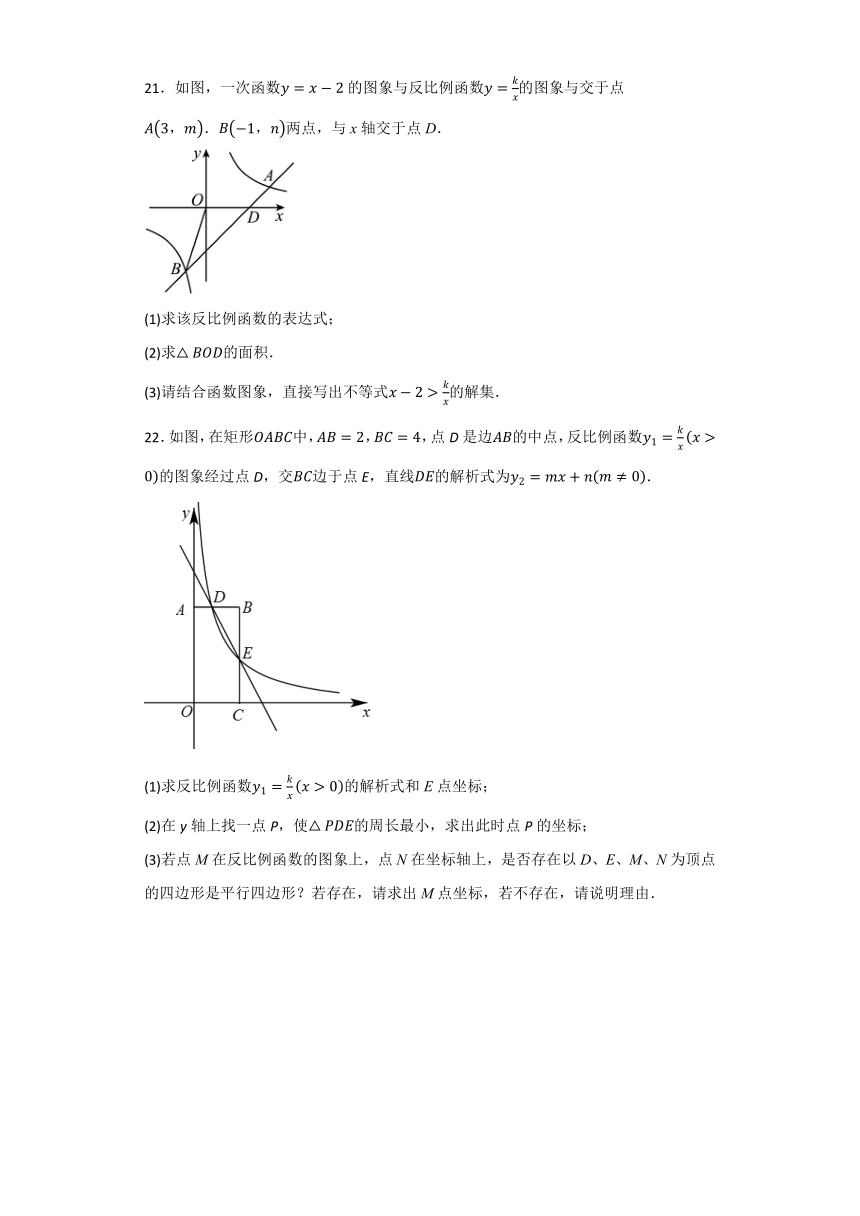
21.如图,一次函数的图象与反比例函数的图象与交于点.两点,与x轴交于点D.
(1)求该反比例函数的表达式;
(2)求的面积.
(3)请结合函数图象,直接写出不等式的解集.
22.如图,在矩形中,,,点D是边的中点,反比例函数的图象经过点D,交边于点E,直线的解析式为.
(1)求反比例函数的解析式和E点坐标;
(2)在y轴上找一点P,使的周长最小,求出此时点P的坐标;
(3)若点M在反比例函数的图象上,点N在坐标轴上,是否存在以D、E、M、N为顶点的四边形是平行四边形?若存在,请求出M点坐标,若不存在,请说明理由.
参考答案
1.解:对于A,C,D选项,给出一个x的值,只有一个y与之相对应,所以不符合题意,对于B,给出一个x的值,不是只有一个y值与之相对应,所以符合题意.
故选:B.
2.解:∵点在第二象限,
∴,
∴,
∴点在第三象限;
故选:C.
3.解:A、当时,,即图象经过点,原说法正确,故此选项符合题意;
B、,图象分布在第一、三象限,原说法错误,故此选项不符合题意;
C、反比例函数的图象可知,图象不关于x轴成轴对称,原说法错误,故此选项不符合题意;
D、,图象分布在第一、三象限,在每个象限内,随的增大而减小,即当时,y随x的增大而减小,原说法错误,故此选项不符合题意.
故选:A.
4.解:由题意得:流出油量是,
则剩余油量:,
故选:B.
5.解:∵直线,,关于y轴对称,
∴点关于y轴的对称点在直线上.
设直线的解析式为,
把点,代入得,
解得,
.令,则,
∴直线,的交点坐标为.
故选:D.
6.解:选项,小时,随着时间的变化,路程也在变化;小时,随着时间的变化,路程不变;小时,随着时间的变化,路程也在变化;及之后,路程在增加,不符合题意;
选项,小时,随着时间的变化,路程也在变化;不符合题意;
选项,小时,随着时间的变化,路程也在变化;不符合题意;
选项,小时,随着时间的变化,路程也在变化;小时,随着时间的变化,路程不变;小时,随着时间的变化,路程也在变化;到小时时,到达山顶,符合题意;
故选:.
7.解:∵双曲线与直线相交于、两点,
∴点与关于原点对称,
∵点坐标为,
∴点的坐标为.
故选:B.
8.解:在中,令,则,
∴,代入中,
得,
∴,
∴,
∴,
故选B.
9.解:由题意,可知:常量是0.58,变量是;
故答案为:0.58;
10.解:∵点B的坐标为,轴,
∴设点A的坐标为,
∵,
∴,
∴或;
∴点A的坐标为 或;
故答案为: 或.
11.解:由题意可得:这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t(小时)之间的函数关系式的是;
故答案为.
12.解:由图象和题意可知:
函数图象在x轴上方(含x轴)对应的x的范围是,
故答案为:.
13.解:设点C的坐标为,则,
,
,解得,
,
点是OB的中点,
,即,
又点在双曲线上,
,
故答案为:4.
14.解:由函数图象,得:
轮船的速度为:,
快艇的速度为:,
∴快艇比轮船每小时多行千米,
故答案为:20.
15.解:当线段最短时,,
从图2可得:,,,,
的周长:
的周长:
故答案为:.
16.解:①由图可得,甲车行驶的速度是,
根据图像可知:甲先出发,甲出发4h后被乙追上,
∴,
∴,
即乙车行驶的速度是,故①②正确;
③由图可得,当乙到达地时,甲乙相距,
∴甲比乙晚到,故③正确;
④由图可得,当乙车在甲车前,且未到达地时,则,解得;
当乙车到达地后时,,解得,
∴甲车行驶或,甲,乙两车相距,故④错误.
故答案为①②③.
17.解:(1)根据题意设y1=,y2=b(x﹣2),即y=y1+y2=+b(x﹣2),
将x=1时,y=1;x=﹣3时,y=13分别代入得:,
解得:k=﹣,b=﹣,
∴解析式为:y=﹣﹣(x﹣2);
(2)将x=3代入解析式得,y=﹣﹣=﹣3,
∴当x=3时,y的值为-3.
18.解:(1)根据图象可知甲运动员用了12s,乙运动员用了12.5s跑完100m,所以甲运动员先到达终点;
故答案为:甲;
(2)根据图象可知乙运动员的速度是.
故答案为:8;
(3)根据图象可知,甲运动员12s时冲线,乙运动员与甲的距离是.
故答案为:4.
19.解:(1)根据题意,晓玲从大桥上的点A走向点B,故晓玲随着时间的增大距A点的路程也增大,故直线表示的是晓玲距A点的路程y(米)与行走时间x(分钟)之间的关系,由图可知,时,晓玲走到了点B的位置.
(2)根据题意,直线表示的是小华距A点的路程y(米)与行走时间x(分钟)之间的关系
故设直线解析式为
代入,,
得
解得
直线解析式为且.
(3)故设直线解析式为
代入,
得
解得
直线解析式为且.
当晓玲与小华相遇时,即直线与直线的交点位置
故
求解得
故晓玲与小华相遇时,距点A的路程为360米.
20.(1)解:设,将点代入,
可得,
∴,故;
(2)当时,,
∴当气体体积为时,气压是;
(3)当时,,
∴为了安全起见,气体的体积应不小于
21.(1)解:把的坐标代入,得:,
∴,
把的坐标代入,得:,
∴反比例函数的解析式为;
(2)解:设直线的解析式为,
把的坐标代入,得:,
∴,
把,代入,得
,解得:,
∴一次函数的解析式为.
在中,令,则,
即直线与x轴交于点.
∴;
(3)解:由图象得,当或时,一次函数图象位于反比例函数的图象的上方,
∴不等式的解集为或.
22.解:(1)是的中点,且
在反比例函数的图象上
反比例函数解析式:
在反比例函数的图象上
和在直线:上
解得:
的解析式为:
(2)作点D关于y轴的对称点,连接交y轴于点P,连接.
点D与点关于y轴的对称
此时的周长最小为:
设直线的解析式:
和在直线上
解得:
直线的解析式:
当时,
的坐标为:
(3)点M在反比例函数的图象上,点N在坐标轴上
①若点N在x轴上,设,
(1)当和为对角线,即
,
解得:
此时:,, DEMN四点共线,故舍去,
不存在满足条件的平行四边形
(2)当和为对角线,即
,
解得:
此时:,,存在满足条件的平行四边形
(3)当和为对角线,即
,
解得:
此时:,,存在满足条件的平行四边形
②若点N在y轴上,设,
(1)当为对角线,即
解得:
此时:,,存在满足条件的平行四边形
(2)当DN和ME为对角线,即
解得:
此时:,,存在满足条件的平行四边形
(3)当DM和NE为对角线,即
,
解得:
此时:,,此时,DEMN四点共线,故舍去
不存在满足条件的平行四边形
综上所述,点M的坐标为或,
期末综合复习训练题(附答案)
一、单选题
1.下列曲线中不能表示y是x的函数的是( )
A.B.C.D.
2.若点在第二象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.关于反比例函数的图象,下列说法正确的是( )
A.图象经过点 B.图象分布在第二、四象限
C.两个分支关于x轴成轴对称 D.当时,y随x的增大而增大
4.油箱中存油升,油从油箱中均匀流出,流速为升/分钟,剩余油量(升)与流出时间t(分钟)的函数关系是( )
A. B. C. D.
5.两条直线,关于轴对称,经过点,经过点,则这两条直线,的交点坐标为( )
A. B. C. D.
6.某游客为爬上千米高的山顶看日出,先用小时爬了千米休息小时后,用小时爬上山顶.游客爬山所用时间与山高间的函数关系用图形表示是( )
A. B. C. D.
7.如图,双曲线与直线相交于、两点,点坐标为,则点坐标为( )
A. B. C. D.
8.已知一次函数和的图像都经过点,且与y轴交于点,为坐标系原点,那么的面积是( )
A. B. C. D.
二、填空题
9.某市居民用电价格是元/(千瓦·时),居民应付电费为元,用电量为千瓦·时,其中常量是 ________,变量是 ______________.
10.若点B的坐标为,轴,且,则点A的坐标为________.
11.一枝蜡烛长20厘米,点燃后每小时燃烧掉5厘米,则这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t(小时)之间的函数关系式的是________.
12.如图,一次函数(,k,b为常数)的图象与x轴交于点,则关于x的不等式的解集是___.
13.如图,Rt△BOC的一条直角边在x轴正半轴上,双曲线过的斜边的中点,与另一直角边相交于点,若的面积是6,则k的值是_______.
14.一艘轮船和一艘快艇沿相同路线从甲港出发匀速行驶至乙港,行驶路程随时间变化的图象如图,则快艇比轮船每小时多行_____千米.
15.如图1,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示线段的长,与之间的关系如图所示,当线段最短时,的周长为,的周长为,________.
16.A,B两地相距,甲、乙两辆汽车从A地出发到B地,均匀速行驶,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距s(km),甲行驶的时间为t(h),s与t的关系如图所示,下列说法:
①甲车行驶的速度是60km/h,乙车行驶的速度是80km/h;
②甲出发4h后被乙追上;
③甲比乙晚到h;
④甲车行驶8h或h,甲,乙两车相距80km;
其中正确的是______.
三、解答题
17.已知y=y1+y2,且y1与x成反比例,y2与x﹣2成正比例,当x=1时,y=1;当x=﹣3时,y=13,求:
(1)y与x之间的函数解析式;
(2)当x=3时,求y的值.
18.如图,甲,乙两名短跑运动员在一次100米赛跑中的路程(m)与时间(s)的关系图象,则:
(1)甲,乙两人中先到达终点的是 ;
(2)乙在这次赛跑中的速度为 m/s.
(3)当先到达终点运动员冲线瞬间,另外一名运动员与他的距离是 米.
19.灞河元朔大桥其设计理念以“千古一舟”为题,象征“舟行古今、跨越时代”的文化内涵,融合西安市花石榴花造型,与奥体中心建筑造型遥相呼应.某天晓玲和小华在元朔大桥上散步,晓玲从大桥上的点A走向点B,同时小华从点B走向点A,晓玲、小华距A点的路程y(米)与行走时间x(分钟)之间的关系如图所示,请结合图象回答下列问题:
(1)晓玲从点A走向点B用了______分钟;
(2)求小华距A点的路程y(米)与行走时间x(分钟)之间的关系式;
(3)求晓玲与小华相遇时距点A的路程.
20.用橡胶或聚脂薄膜材斜制成气球,并充以比空气密度小的氢气或氦气,用以携带仪器升空,进行高空气象观测.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压与气体体积成反比例函数,其图象如图所示.
(1)求这个函数的表达式.
(2)当气体体积为时,气压是多少?
(3)当气球内的气压大于时,气球将煤炸,为了安全起见,气体的体积应不小于多少?
21.如图,一次函数的图象与反比例函数的图象与交于点.两点,与x轴交于点D.
(1)求该反比例函数的表达式;
(2)求的面积.
(3)请结合函数图象,直接写出不等式的解集.
22.如图,在矩形中,,,点D是边的中点,反比例函数的图象经过点D,交边于点E,直线的解析式为.
(1)求反比例函数的解析式和E点坐标;
(2)在y轴上找一点P,使的周长最小,求出此时点P的坐标;
(3)若点M在反比例函数的图象上,点N在坐标轴上,是否存在以D、E、M、N为顶点的四边形是平行四边形?若存在,请求出M点坐标,若不存在,请说明理由.
参考答案
1.解:对于A,C,D选项,给出一个x的值,只有一个y与之相对应,所以不符合题意,对于B,给出一个x的值,不是只有一个y值与之相对应,所以符合题意.
故选:B.
2.解:∵点在第二象限,
∴,
∴,
∴点在第三象限;
故选:C.
3.解:A、当时,,即图象经过点,原说法正确,故此选项符合题意;
B、,图象分布在第一、三象限,原说法错误,故此选项不符合题意;
C、反比例函数的图象可知,图象不关于x轴成轴对称,原说法错误,故此选项不符合题意;
D、,图象分布在第一、三象限,在每个象限内,随的增大而减小,即当时,y随x的增大而减小,原说法错误,故此选项不符合题意.
故选:A.
4.解:由题意得:流出油量是,
则剩余油量:,
故选:B.
5.解:∵直线,,关于y轴对称,
∴点关于y轴的对称点在直线上.
设直线的解析式为,
把点,代入得,
解得,
.令,则,
∴直线,的交点坐标为.
故选:D.
6.解:选项,小时,随着时间的变化,路程也在变化;小时,随着时间的变化,路程不变;小时,随着时间的变化,路程也在变化;及之后,路程在增加,不符合题意;
选项,小时,随着时间的变化,路程也在变化;不符合题意;
选项,小时,随着时间的变化,路程也在变化;不符合题意;
选项,小时,随着时间的变化,路程也在变化;小时,随着时间的变化,路程不变;小时,随着时间的变化,路程也在变化;到小时时,到达山顶,符合题意;
故选:.
7.解:∵双曲线与直线相交于、两点,
∴点与关于原点对称,
∵点坐标为,
∴点的坐标为.
故选:B.
8.解:在中,令,则,
∴,代入中,
得,
∴,
∴,
∴,
故选B.
9.解:由题意,可知:常量是0.58,变量是;
故答案为:0.58;
10.解:∵点B的坐标为,轴,
∴设点A的坐标为,
∵,
∴,
∴或;
∴点A的坐标为 或;
故答案为: 或.
11.解:由题意可得:这枝蜡烛点燃后剩下的长度h(厘米)与点燃时间t(小时)之间的函数关系式的是;
故答案为.
12.解:由图象和题意可知:
函数图象在x轴上方(含x轴)对应的x的范围是,
故答案为:.
13.解:设点C的坐标为,则,
,
,解得,
,
点是OB的中点,
,即,
又点在双曲线上,
,
故答案为:4.
14.解:由函数图象,得:
轮船的速度为:,
快艇的速度为:,
∴快艇比轮船每小时多行千米,
故答案为:20.
15.解:当线段最短时,,
从图2可得:,,,,
的周长:
的周长:
故答案为:.
16.解:①由图可得,甲车行驶的速度是,
根据图像可知:甲先出发,甲出发4h后被乙追上,
∴,
∴,
即乙车行驶的速度是,故①②正确;
③由图可得,当乙到达地时,甲乙相距,
∴甲比乙晚到,故③正确;
④由图可得,当乙车在甲车前,且未到达地时,则,解得;
当乙车到达地后时,,解得,
∴甲车行驶或,甲,乙两车相距,故④错误.
故答案为①②③.
17.解:(1)根据题意设y1=,y2=b(x﹣2),即y=y1+y2=+b(x﹣2),
将x=1时,y=1;x=﹣3时,y=13分别代入得:,
解得:k=﹣,b=﹣,
∴解析式为:y=﹣﹣(x﹣2);
(2)将x=3代入解析式得,y=﹣﹣=﹣3,
∴当x=3时,y的值为-3.
18.解:(1)根据图象可知甲运动员用了12s,乙运动员用了12.5s跑完100m,所以甲运动员先到达终点;
故答案为:甲;
(2)根据图象可知乙运动员的速度是.
故答案为:8;
(3)根据图象可知,甲运动员12s时冲线,乙运动员与甲的距离是.
故答案为:4.
19.解:(1)根据题意,晓玲从大桥上的点A走向点B,故晓玲随着时间的增大距A点的路程也增大,故直线表示的是晓玲距A点的路程y(米)与行走时间x(分钟)之间的关系,由图可知,时,晓玲走到了点B的位置.
(2)根据题意,直线表示的是小华距A点的路程y(米)与行走时间x(分钟)之间的关系
故设直线解析式为
代入,,
得
解得
直线解析式为且.
(3)故设直线解析式为
代入,
得
解得
直线解析式为且.
当晓玲与小华相遇时,即直线与直线的交点位置
故
求解得
故晓玲与小华相遇时,距点A的路程为360米.
20.(1)解:设,将点代入,
可得,
∴,故;
(2)当时,,
∴当气体体积为时,气压是;
(3)当时,,
∴为了安全起见,气体的体积应不小于
21.(1)解:把的坐标代入,得:,
∴,
把的坐标代入,得:,
∴反比例函数的解析式为;
(2)解:设直线的解析式为,
把的坐标代入,得:,
∴,
把,代入,得
,解得:,
∴一次函数的解析式为.
在中,令,则,
即直线与x轴交于点.
∴;
(3)解:由图象得,当或时,一次函数图象位于反比例函数的图象的上方,
∴不等式的解集为或.
22.解:(1)是的中点,且
在反比例函数的图象上
反比例函数解析式:
在反比例函数的图象上
和在直线:上
解得:
的解析式为:
(2)作点D关于y轴的对称点,连接交y轴于点P,连接.
点D与点关于y轴的对称
此时的周长最小为:
设直线的解析式:
和在直线上
解得:
直线的解析式:
当时,
的坐标为:
(3)点M在反比例函数的图象上,点N在坐标轴上
①若点N在x轴上,设,
(1)当和为对角线,即
,
解得:
此时:,, DEMN四点共线,故舍去,
不存在满足条件的平行四边形
(2)当和为对角线,即
,
解得:
此时:,,存在满足条件的平行四边形
(3)当和为对角线,即
,
解得:
此时:,,存在满足条件的平行四边形
②若点N在y轴上,设,
(1)当为对角线,即
解得:
此时:,,存在满足条件的平行四边形
(2)当DN和ME为对角线,即
解得:
此时:,,存在满足条件的平行四边形
(3)当DM和NE为对角线,即
,
解得:
此时:,,此时,DEMN四点共线,故舍去
不存在满足条件的平行四边形
综上所述,点M的坐标为或,
