22.4(1)几何证明之角的相等[上学期]
文档属性
| 名称 | 22.4(1)几何证明之角的相等[上学期] |
|
|
| 格式 | zip | ||
| 文件大小 | 41.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-09 00:00:00 | ||
图片预览

文档简介
第二十二章 几何证明
22.4几何证明举例
教学目的:
1、 掌握几何证明的基本方法,学会分析、推理论证,强调每一步推理言必有据
2、 运用学过的平行线判定及性质,全等三角形判定性质,等腰三角形判定性质等进行正确的推理论证。
教学重点:掌握几何证明的推理方法,做到言必有据
教学难点:证明题目的思路
教学过程:
如何证明角相等?
例:与平行线有关的证明角相等。
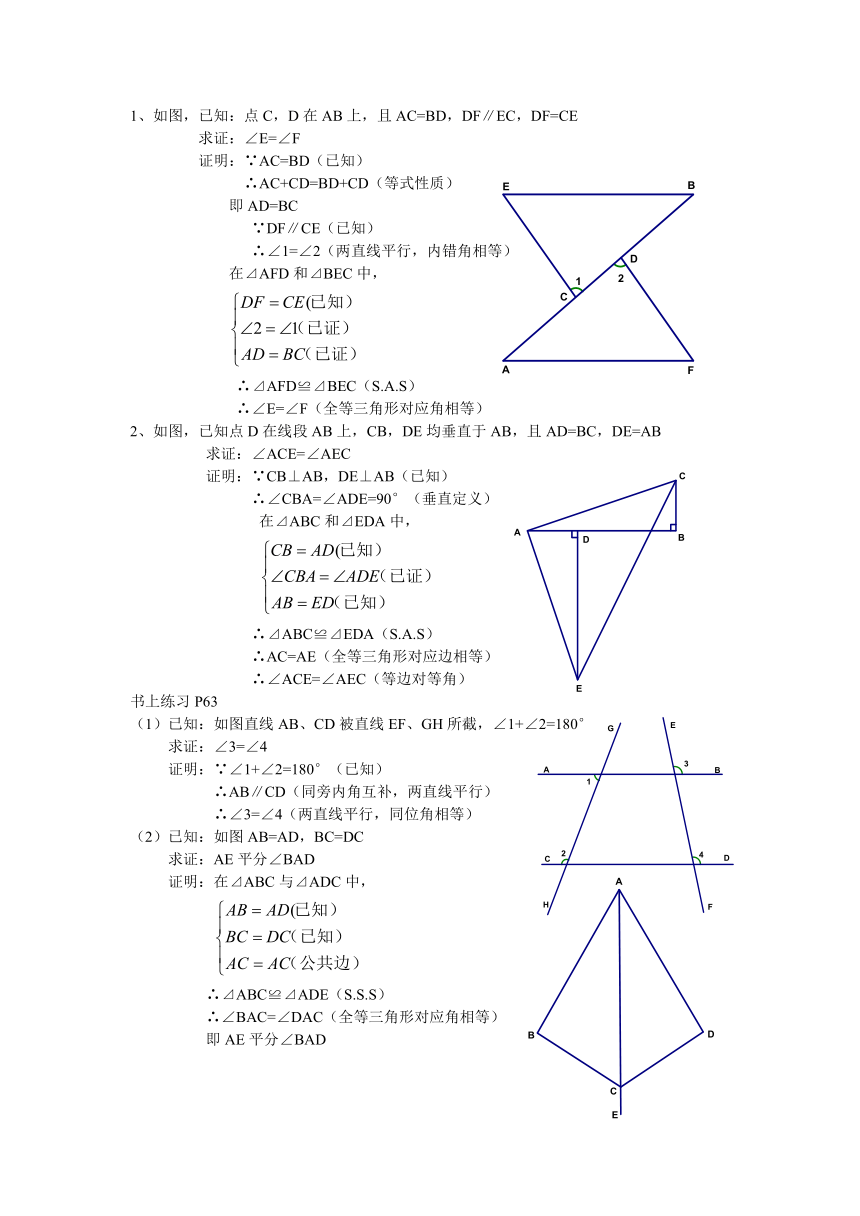
1、已知:如图,∠1=∠2
求证:∠3=∠4
证明:∵∠1 = ∠2(已知)
∴AB∥CD(同位角相等,两直线平行)
∴∠3=∠5(两直线平行,同位角相等)
∵∠4=∠5(对顶角相等)
∴∠3=∠4(等量代换)
2、如图,已知⊿ABC的外角平分线AD∥BC
求证:∠B=∠C
证明:∵AD平分EAC(已知)
∴∠1=∠2(角平分线定义)
∵AD∥BC(已知)
∴∠1=∠B(两直线平行,同位角相等
∠2=∠C(两直线平行,内错角相等)
∴∠B=∠C(等量代换)
3、 如图,已知:∠1=∠2,∠C=∠D
求证:∠A=∠F
证明一:∵∠1=∠3,∠2=∠4(对顶角相等)
∴∠1=∠2(已知)
∴∠3=∠4(等量代换)
∵∠D+∠F+∠3=180°,∠C+∠A+∠4=180°(三角形内角和180°)
又∵∠C=∠D(已知)
∴∠A=∠F(等式性质)
证明二:∵∠1=∠3(对顶角相等)
又∵∠1=∠2(已知)
∴∠2=∠3 (等量代换)
∴EC∥DB(同位角相等,两直线平行)
∴∠C=∠5(两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠5=∠D(等量代换)
∴DF∥BC(内错角相等,两直线平行)
∴∠A=∠F(两直线平行,内错角相等)
例:与全等有关的证明角相等。
1、如图,已知:点C,D在AB上,且AC=BD,DF∥EC,DF=CE
求证:∠E=∠F
证明:∵AC=BD(已知)
∴AC+CD=BD+CD(等式性质)
即AD=BC
∵DF∥CE(已知)
∴∠1=∠2(两直线平行,内错角相等)
在⊿AFD和⊿BEC中,
∴⊿AFD≌⊿BEC(S.A.S)
∴∠E=∠F(全等三角形对应角相等)
2、如图,已知点D在线段AB上,CB,DE均垂直于AB,且AD=BC,DE=AB
求证:∠ACE=∠AEC
证明:∵CB⊥AB,DE⊥AB(已知)
∴∠CBA=∠ADE=90°(垂直定义)
在⊿ABC和⊿EDA中,
∴⊿ABC≌⊿EDA(S.A.S)
∴AC=AE(全等三角形对应边相等)
∴∠ACE=∠AEC(等边对等角)
书上练习P63
(1)已知:如图直线AB、CD被直线EF、GH所截,∠1+∠2=180°
求证:∠3=∠4
证明:∵∠1+∠2=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠3=∠4(两直线平行,同位角相等)
(2)已知:如图AB=AD,BC=DC
求证:AE平分∠BAD
证明:在⊿ABC与⊿ADC中,
∴⊿ABC≌⊿ADE(S.S.S)
∴∠BAC=∠DAC(全等三角形对应角相等)
即AE平分∠BAD
(3)已知:如图:BE=CF,∠ACB=∠DFE,AC=DF
求证:AB∥DE
证明:∵BE=CF(已知)
∴BE+EC=CF+EC(等式性质)
即BC=EF
在⊿ACB与⊿DFE中,
∴⊿ACB≌⊿DFE(S.A.S)
∴∠ABC=∠DEF(全等三角形对应角相等)
∴AB∥DE(同位角相等,两直线平行)
(4)已知:如图AB=AC,∠BAO=∠CAO
求证:∠OBC=∠OCB
证明:在⊿BAO和⊿CAO中,
∴⊿BAO≌⊿CAO(S.A.S)
∴OB=OC(全等三角形对应边相等)
∴∠OBC=∠OCB(等边对等角)
总结:证明“角相等”的思考步骤:
第一层次:对顶角相等 (定理3)
角平分线定义
第二层次:同(等)角的雨(补)角相等 (定理1,2)
两直线平行,同位角相等 (公理4)
两直线平行,内错角相等 (定理12)
第三层次:在同一个三角形中,等边对等角 (定理17)
全等三角形对应角相等 (定理41)
等腰三角形底边上的中线(底边上的高)平分顶角 (定理18)
等边三角形的三个内角都相等,并且每一个内角都等于60度。(定理20)
在同(等)圆中,如果弦(弦心距,弧)相等,则所对的圆心角相等。
(定理25,26,27)
平行四边形对角相等 (定理36)
等式性质与等量代换
*一般需要证明的两个角在同一个三角形中,多用等边对等角;在不同的三角形中,多用全等三角形对应角相等;平行线较多,多用平行线的性质;直角比较多时,多用等角的余角相等。
习题精练:
1、已知:如图,AD=AC,BD=BC
求证:∠1=∠2
2、已知:⊿ABC的三个内角平分线相交于点O,过O作OG⊥BC垂足为G
求证∠BOD=∠COG
3、已知:等腰⊿ABC的底边BC上两点P、Q,按B,P,Q,C的顺序,取BP=QC,
在AB、AC上分别取D,E点,使AD=AE,DQ与EP交于点O
求证:AO平分∠BAC
4、 已知:∠BAD=∠CAD,DE∥AC交AB于E交AB于E,EF⊥AD交BC于F
求证:∠B=∠FAC
作业:
1、 A册/22.4(1)
2、 同步
3、 一课一练
22.4几何证明举例
教学目的:
1、 掌握几何证明的基本方法,学会分析、推理论证,强调每一步推理言必有据
2、 运用学过的平行线判定及性质,全等三角形判定性质,等腰三角形判定性质等进行正确的推理论证。
教学重点:掌握几何证明的推理方法,做到言必有据
教学难点:证明题目的思路
教学过程:
如何证明角相等?
例:与平行线有关的证明角相等。
1、已知:如图,∠1=∠2
求证:∠3=∠4
证明:∵∠1 = ∠2(已知)
∴AB∥CD(同位角相等,两直线平行)
∴∠3=∠5(两直线平行,同位角相等)
∵∠4=∠5(对顶角相等)
∴∠3=∠4(等量代换)
2、如图,已知⊿ABC的外角平分线AD∥BC
求证:∠B=∠C
证明:∵AD平分EAC(已知)
∴∠1=∠2(角平分线定义)
∵AD∥BC(已知)
∴∠1=∠B(两直线平行,同位角相等
∠2=∠C(两直线平行,内错角相等)
∴∠B=∠C(等量代换)
3、 如图,已知:∠1=∠2,∠C=∠D
求证:∠A=∠F
证明一:∵∠1=∠3,∠2=∠4(对顶角相等)
∴∠1=∠2(已知)
∴∠3=∠4(等量代换)
∵∠D+∠F+∠3=180°,∠C+∠A+∠4=180°(三角形内角和180°)
又∵∠C=∠D(已知)
∴∠A=∠F(等式性质)
证明二:∵∠1=∠3(对顶角相等)
又∵∠1=∠2(已知)
∴∠2=∠3 (等量代换)
∴EC∥DB(同位角相等,两直线平行)
∴∠C=∠5(两直线平行,同位角相等)
∵∠C=∠D(已知)
∴∠5=∠D(等量代换)
∴DF∥BC(内错角相等,两直线平行)
∴∠A=∠F(两直线平行,内错角相等)
例:与全等有关的证明角相等。
1、如图,已知:点C,D在AB上,且AC=BD,DF∥EC,DF=CE
求证:∠E=∠F
证明:∵AC=BD(已知)
∴AC+CD=BD+CD(等式性质)
即AD=BC
∵DF∥CE(已知)
∴∠1=∠2(两直线平行,内错角相等)
在⊿AFD和⊿BEC中,
∴⊿AFD≌⊿BEC(S.A.S)
∴∠E=∠F(全等三角形对应角相等)
2、如图,已知点D在线段AB上,CB,DE均垂直于AB,且AD=BC,DE=AB
求证:∠ACE=∠AEC
证明:∵CB⊥AB,DE⊥AB(已知)
∴∠CBA=∠ADE=90°(垂直定义)
在⊿ABC和⊿EDA中,
∴⊿ABC≌⊿EDA(S.A.S)
∴AC=AE(全等三角形对应边相等)
∴∠ACE=∠AEC(等边对等角)
书上练习P63
(1)已知:如图直线AB、CD被直线EF、GH所截,∠1+∠2=180°
求证:∠3=∠4
证明:∵∠1+∠2=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠3=∠4(两直线平行,同位角相等)
(2)已知:如图AB=AD,BC=DC
求证:AE平分∠BAD
证明:在⊿ABC与⊿ADC中,
∴⊿ABC≌⊿ADE(S.S.S)
∴∠BAC=∠DAC(全等三角形对应角相等)
即AE平分∠BAD
(3)已知:如图:BE=CF,∠ACB=∠DFE,AC=DF
求证:AB∥DE
证明:∵BE=CF(已知)
∴BE+EC=CF+EC(等式性质)
即BC=EF
在⊿ACB与⊿DFE中,
∴⊿ACB≌⊿DFE(S.A.S)
∴∠ABC=∠DEF(全等三角形对应角相等)
∴AB∥DE(同位角相等,两直线平行)
(4)已知:如图AB=AC,∠BAO=∠CAO
求证:∠OBC=∠OCB
证明:在⊿BAO和⊿CAO中,
∴⊿BAO≌⊿CAO(S.A.S)
∴OB=OC(全等三角形对应边相等)
∴∠OBC=∠OCB(等边对等角)
总结:证明“角相等”的思考步骤:
第一层次:对顶角相等 (定理3)
角平分线定义
第二层次:同(等)角的雨(补)角相等 (定理1,2)
两直线平行,同位角相等 (公理4)
两直线平行,内错角相等 (定理12)
第三层次:在同一个三角形中,等边对等角 (定理17)
全等三角形对应角相等 (定理41)
等腰三角形底边上的中线(底边上的高)平分顶角 (定理18)
等边三角形的三个内角都相等,并且每一个内角都等于60度。(定理20)
在同(等)圆中,如果弦(弦心距,弧)相等,则所对的圆心角相等。
(定理25,26,27)
平行四边形对角相等 (定理36)
等式性质与等量代换
*一般需要证明的两个角在同一个三角形中,多用等边对等角;在不同的三角形中,多用全等三角形对应角相等;平行线较多,多用平行线的性质;直角比较多时,多用等角的余角相等。
习题精练:
1、已知:如图,AD=AC,BD=BC
求证:∠1=∠2
2、已知:⊿ABC的三个内角平分线相交于点O,过O作OG⊥BC垂足为G
求证∠BOD=∠COG
3、已知:等腰⊿ABC的底边BC上两点P、Q,按B,P,Q,C的顺序,取BP=QC,
在AB、AC上分别取D,E点,使AD=AE,DQ与EP交于点O
求证:AO平分∠BAC
4、 已知:∠BAD=∠CAD,DE∥AC交AB于E交AB于E,EF⊥AD交BC于F
求证:∠B=∠FAC
作业:
1、 A册/22.4(1)
2、 同步
3、 一课一练
