第一章特殊平行四边形学案

第一章 特殊平行四边形
一、 矩 形
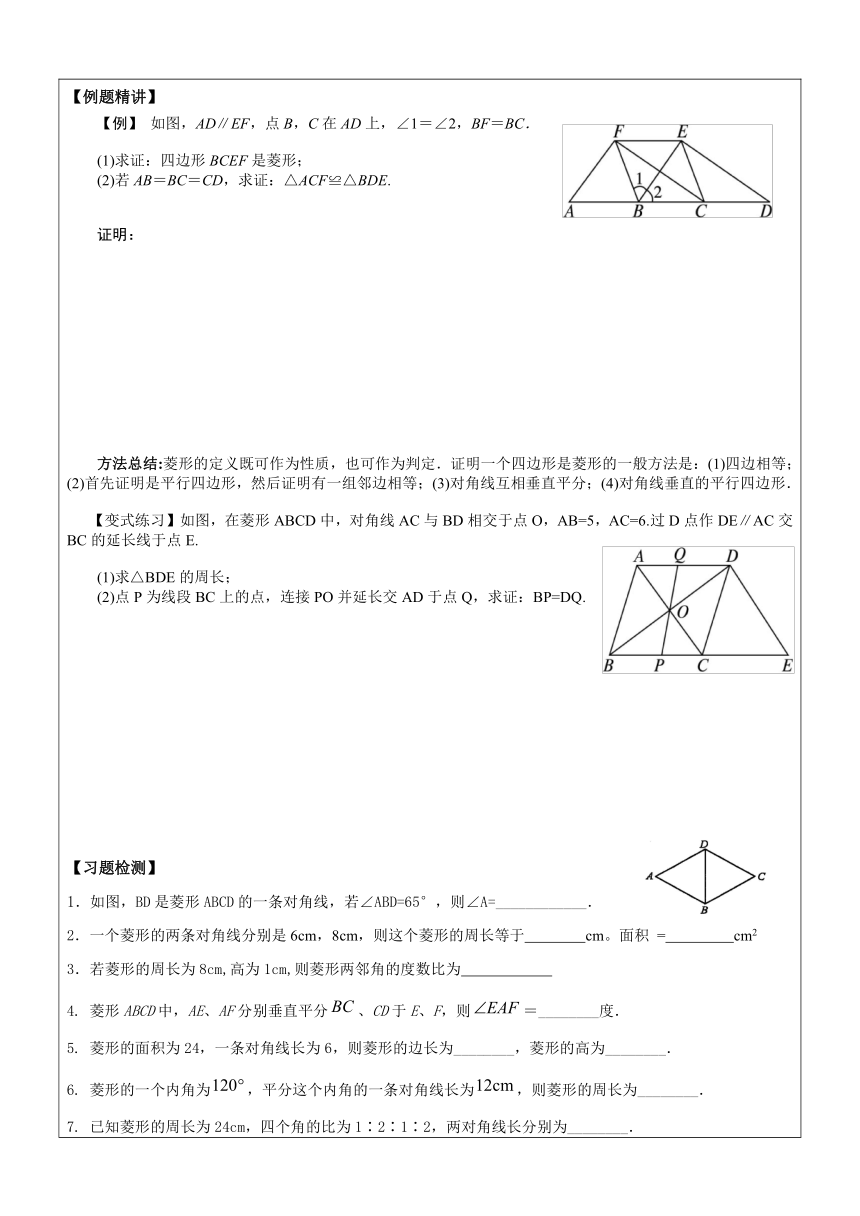
【知识点总结】1、矩形的定义：__________________________的平行四边形叫矩形．2、矩形的性质：①．矩形的四个角都是______；矩形的对角线__________________________． ②.矩形既是 对称图形,又是 图形,它有 条对称轴.3、矩形的判定：①．有_____个是直角的四边形是矩形．②．对角线____________________________的平行四边形是矩形．③．对角线________________________________的四边形是矩形．【例题精讲】 【例1】 如图，△ABC中，AB＝AC，AD，AE分别是∠BAC和∠BAC外角的平分线，BE⊥AE. ( http: / / www.21cnjy.com )(1)求证：DA⊥AE；(2)试判断AB与DE是否相等，并证明你的结论．分析：第(1)题利用邻补角的角平分线互相垂直易证；第(2)题中，AB与DE是四边形ADBE的对角线，可考虑利用矩形的判定证四边形ADBE是矩形即可．解：方法总结:矩形的定义既可以作为性质，也可 ( http: / / www.21cnjy.com )以作为判定．矩形的性质是求证线段或角相等时常用的知识点．证明一个四边形是矩形的方法：(1)先证明它是平行四边形，再证明它有一个角是直角；(2)先证明它是平行四边形，再证明它的对角线相等；(3)证明有三个内角为90°.【变式练习】如图，将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，连接AE.求证：(1)BF＝DF；(2)AE∥BD.【习题检测】1．如果矩形的一条对角线与一边的夹角为40°,那么两条对角线所夹钝角的度数为 。2．四边形ABCD的对角线AC，BD相交于点O，能判断它为矩形的题设是（ ） A．AO=CO，BO=DO B．AO=BO=CO=DOC．AB=BC，AO=CO D．AO=CO，BO=DO，AC⊥BD3．如图，ADBC，则四边形ABCD是______，又对角线AC，BD交于点O，若∠1=∠2，则四边形ABCD是______．4.一个矩形的两条对角线的交点到小边的距离比到大边的距离多2cm，若这个矩形的周长是56cm，则它的面积是（ ）A、48cm2 B、192cm2 C、196cm2 D、以上答案都不对下列说法不能说明四边形是矩形的是 （ ） A.三个角是直角的四边形 B.对角线相等的平行四边形 C.对角线垂直且相等的平行四边形 D.四个角都相等的四边形6.下列性质中，矩形具有而平行四边形不具有的是 （ ）A、对边平行 B、对角相等 C、对边相等 D、对角线相等7.如图，矩形ABCD中，AB=2cm，BD=4cm，AE⊥BD，E是垂足，求AC的长和∠ADB、∠BAE的度数。二、菱 形【知识点总结】1、菱形的定义：有一组_________________________相等的平行四边形叫菱形．2、菱形的性质：①．菱形的四条边______；菱形的对角线_____________，且每条对角线______________． ②.菱形既是 对称图形,又是 图形,它有 条对称轴.3、菱形的判定：①．__________________边都相等的四边形菱形．②．对角线_____________________________的平行四边形是菱形．③．对角线_____________________________________________的四边形是菱形．4、菱形的面积与两对角线的关系是________________________【例题精讲】【例】 如图，AD∥EF，点B，C在AD上，∠1＝∠2，BF＝BC．(1)求证：四边形BCEF是菱形；(2)若AB＝BC＝CD，求证：△ACF≌△BDE.证明：方法总结:菱形的定义既可作为性质，也可作为 ( http: / / www.21cnjy.com )判定．证明一个四边形是菱形的一般方法是：(1)四边相等；(2)首先证明是平行四边形，然后证明有一组邻边相等；(3)对角线互相垂直平分；(4)对角线垂直的平行四边形． 【变式练习】如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=5，AC=6.过D点作DE∥AC交BC的延长线于点E. (1)求△BDE的周长；(2)点P为线段BC上的点，连接PO并延长交AD于点Q，求证：BP=DQ.【习题检测】1．如图，BD是菱形ABCD的一条对角线，若∠ABD=65°，则∠A=____________．2．一个菱形的两条对角线分别是6cm，8cm，则这个菱形的周长等于 cm。面积 = cm23．若菱形的周长为8cm,高为1cm,则菱形两邻角的度数比为 4. 菱形ABCD中，AE、AF分别垂直平分、CD于E、F，则＝________度．5. 菱形的面积为24，一条对角线长为6，则菱形的边长为________，菱形的高为________．6. 菱形的一个内角为，平分这个内角的一条对角线长为，则菱形的周长为________．7. 已知菱形的周长为24cm，四个角的比为1∶2∶1∶2，两对角线长分别为________．8. 已知菱形的一条对角线长为8cm，周长为32cm，则菱形的四个角分别为________．9. 从菱形的钝角顶点向对边引垂线，如果垂线平分对边，则菱形四个角的度数分别为_______．10. 已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AE=2。求（1）∠ABC的度数； （2）对角线AC、BD的长； （3）菱形ABCD的面积。三、正 方 形【知识点总结】1、正方形的定义： 的平行四边形叫正方形。2、正方形的性质：①．正方形的四个角是_____角，四条边_____，对角线_______________________．②．正方形是______对称图形，又是 对称图形,它有_________条对称轴．3．正方形的判定：先判定这个四边形是矩形，再判定这个矩形还是_________形；或者先判定四边形是菱形，再判定这个菱形也是___________形．【例题精讲】【例4】 如图①，在正方形ABCD中，E，F，G，H分别为边AB，BC，CD，DA上的点，HA＝EB＝FC＝GD，连接EG，FH，交点为O.(1)如图②，连接EF，FG，GH，HE，试判断四边形EFGH的形状，并证明你的结论； ( http: / / www.21cnjy.com )(2)将正方形ABCD沿线段EG，HF剪开，再把得到的四个四边形按图③的方式拼接成一个四边形．若正方形ABCD的边长为3 cm，HA＝EB＝FC＝GD＝1 cm，则图③中阴影部分的面积为__________cm2.分析：根据题目的条件可先证△AEH，△BFE，△CGF，△DHG四个三角形全等，证得四边形EFGH的四边相等，然后由全等再证一个角是直角．解：方法总结:证明一个四边形是正方形可从以下几个方面考虑：(1)“平行四边形”+“一组邻边相等”+“一个角为直角”； (2)“矩形”＋“一组邻边相等”；(3)“矩形”＋“对角线互相垂直”；(4)“菱形”＋“一个角为直角”；(5)“菱形”＋“对角线相等”．【习题检测】①正方形的面积为4，则它的边长为______________，对角线长为____________．②已知正方形的对角线长是4，则它的边长是 ，面积是 .③如图所示，在△ABC中，AB=AC，点D，E，F分别是边AB，BC，AC的中点，连接DE，EF，要使四边形ADEF是正方形，还需增加条件：_______．特殊平行四边形检测题一、选择题1、矩形ABCD的长AC=15cm，宽AB=10cm，∠ABC的平分线分AD边为AE、ED两部分，这AE、ED的长分别为（ ） A．4cm和11cm B．5cm和10cm C．6cm和9cm D．7cm和8cm2、四边形ABCD的对角线互相平分，要使它变为矩形，需要添加的条件是（ ） A．AB=CD B．AD=BC C．AB=BC D．AC=BD3、如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEBO （ ）A. 10° B．15° C．20° D．12.5°4、如图，在菱形 ABCD中，E、F分别是AD、BD的中点，如果EF=2，那么菱形ABCD的周长是（ ）A. 4 B．8 C．12 D．16二、填空题5、已知正方形ABCD对角线AC，BD相交于点O，且AC=16cm，则DO=_____cm，BO=____cm，∠OCD=____度．6、在平面直角坐标系中，四边形ABCD是菱形，∠ABC=60°，且点A的坐标为（0，2）,则点B坐标（ ），点C坐标为（ ），点D坐标为（ ）。7、一平行四边形的一条边长是9，两条对角线长分别是12和 ，它是 形，它的面积是 ，周长是 。8、如图ABCD是一块正方形场地，在AB边上取定了一点E，量得EC=30 cm，EB=10 cm，则这块场地的面积是 cm2，对角线的长是 cm.三、解答题9、如图，四边形ABCD是菱形 ，∠ACD=30°,BD=6,求:（1）∠BAD,∠ABC的度数（2）边AB及对角线AC的长（精确到0.01cm）10、在Rt△ABC中，∠ACB=90°CD⊥AB于点D，∠ACD=3∠BCD，点E是斜边AB的中点，求∠ECD的度数。11、如图，四边形ABCD是菱形，对角线AC=8cm，DB=6cm,DH⊥AB于点H，求DH的长.12、如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD，求证：四边形OCED是菱形。13、如图：AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD，求证：四边形ABCD是菱形14、如图，E、F、M、N分别是正方形ABCD四条边上的点，且AE=BF=CM=DN，求证，四边形EFMN是正方形 。15、如图，点E、F在正方形ABCD的边BC、CD上，AE、BF相交于点G，BE=CF求证：（1）AE=BF。（2）AE⊥BF。
A
B
D
E
C
A
B
C
D
E
E
F
x
y
A
B
D
0
C
B
A
C
D
E
A
B
C
D
E
H
A
B
C
D
E
O
A
B
C
D
O
E
F
A
B
C
D
E
F
M
N
A
B
C
D
E
G
F