矩形性质和判定学案

矩形的性质学案
(1)【课标考纲解读】
利用矩形的性质进行有关的计算和证明。
(2)【状元学习方案】
经历探索矩形的概念和性质的过程，渗透运动联系，从量变到质变的观点；
2．【学习目标】
知识目标：学习矩形的性质，能正确的推导出矩形的性质.
能力目标：利用矩形的性质进行有关计算和证明.
情感目标：通过小组的合作讨论，培养学生的合作精神和学习信心。
3．【重难点】
教学重点：利用矩形的性质进行推理和证明．
教学难点：证明的严谨性及独立分析和解决问题的培养。
4．【学法指导】
通过探究学习，培养学生严谨的推理能力，体会逻辑推理的思维价值。
5．【学习过程】
一、知识链接：回顾平行四边形有哪些性质？然后填空。
1、平行四边形的__________相等。表示方法：若四边形ABCD是平行四边形，则___________;
2、平行四边形的__________相等。表示方法：若四边形ABCD是平行四边形，则___________;
3、平行四边形的对角线________.表示方法：在□ ABCD中，AC与BD相交于O，则______________
4、平行四边形的对称性：平行四边形是___对称图形，而不是______对称图形，对角线的交点是平行四边形的_________.
二、学习新知：自学P94-95页。
自学引导：①平行四边形活动框架在变化过程中，哪些量发生了变化？哪些量没有变化？从中得到哪些结论？你能试着说明结论是否成立？
②矩形的一条对角线把矩形分成两个什么三角形？矩形的两条对角线把矩形分成四个什么样的三角形？
1．矩形的定义：有一个角是直角的平行四边形，叫做矩形。由此可见，矩形是特殊的 ，它具有平行四边形的所有性质。
2．结合上面两个图形说说矩形有哪些平行四边形不具有的特殊性质？
.
3．证明：矩形的四个角都是直角
已知：如图， 图形：画在下面
求证：___________________
证明：
4.证明：矩形对角线相等
已知：如图， 图形：画在下面
求证：
证明：
三、探索活动
问题一 如图，矩形ABCD，对角线相交于O，观察对角线所分成的三角形，你有什么发现？
( http: / / www.21cnjy.com / )
问题二 将目光锁定在Rt△ABC中，你能发现它有什么特殊的性质吗？
证明：“直角三角形斜边上的中线等于斜边的一半．”
已知： 图形：画在下面
求证：
证明：
问题三 上面结论的逆命题是： 。
是否正确？请给予证明。
四、例题学习
例1.如图，矩形ABCD的两条对角线相交于点O，∠AOB=60°,AB=4cm，求矩形对角线的长。
同类练习：已知：如图，矩形ABCD的两条对角线相交于点O，且AC=2AB。求证：△AOB是等边三角形。(注意表达格式完整性与逻辑性)
拓展与延伸：本题若将“AC=2AB”改为“∠BOC=120°”，你能获得有关这个矩形的哪些结论？
五、课堂练习
【A组】1、课本95页，练习1、3（答案写在课本上）
2、已知：如图，E为矩形ABCD内一点，且EB=EC。求证：EA=ED.
( http: / / www.21cnjy.com / )
【B组】3、如图，矩形纸片ABCD中，AB=4，AD=3，折叠纸片使AD边与对角线BD重合，折痕为DG，则AG的长为（ ）
A．1 B． C． D．2
六、提高训练：
【A组】1.已知：如图，矩形ABCD的两 ( http: / / www.21cnjy.com )条对角线AC、BD相交于点O，∠BOC=120°，AB=4cm。求矩形对角线的长。（提示：通过类比例1，解这道题）
( http: / / www.21cnjy.com / )
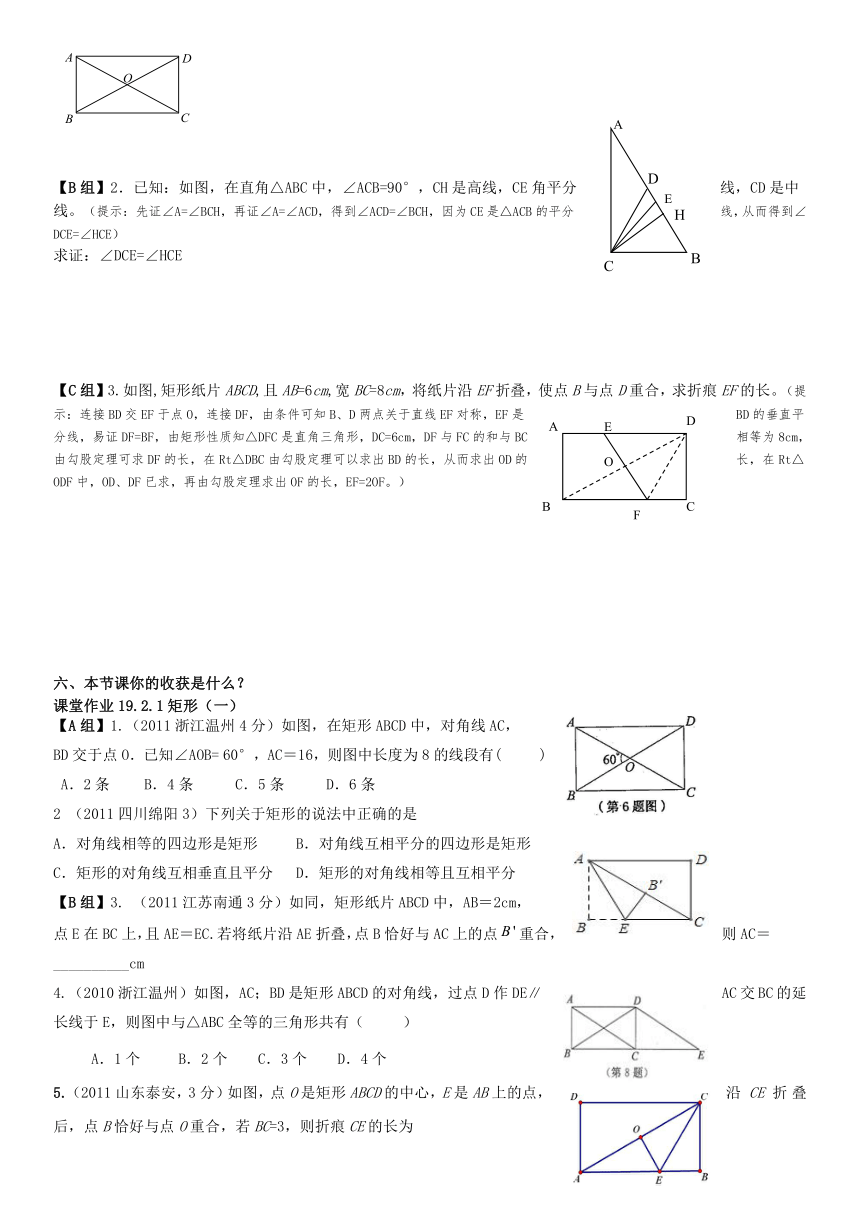
【B组】2．已知：如图，在直角△ABC中， ( http: / / www.21cnjy.com )∠ACB=90°，CH是高线，CE角平分线，CD是中线。（提示：先证∠A=∠BCH，再证∠A=∠ACD，得到∠ACD=∠BCH，因为CE是△ACB的平分线，从而得到∠DCE=∠HCE）
求证：∠DCE=∠HCE
【C组】3.如图,矩形纸片ABCD,且AB ( http: / / www.21cnjy.com )=6cm,宽BC=8cm，将纸片沿EF折叠，使点B与点D重合，求折痕EF的长。（提示：连接BD交EF于点O，连接DF，由条件可知B、D两点关于直线EF对称，EF是BD的垂直平分线，易证DF=BF，由矩形性质知△DFC是直角三角形，DC=6cm，DF与FC的和与BC相等为8cm，由勾股定理可求DF的长，在Rt△DBC由勾股定理可以求出BD的长，从而求出OD的长，在Rt△ODF中，OD、DF已求，再由勾股定理求出OF的长，EF=2OF。）
六、本节课你的收获是什么？
课堂作业19.2.1矩形（一）
【A组】1.（2011浙江温州4分）如图，在矩形ABCD中，对角线AC，
BD交于点O．已知∠AOB= 60°，AC＝16，则图中长度为8的线段有( )
A．2条 B．4条 C．5条 D．6条
2 （2011四川绵阳3）下列关于矩形的说法中正确的是
A．对角线相等的四边形是矩形 B．对角线互相平分的四边形是矩形
C．矩形的对角线互相垂直且平分 D．矩形的对角线相等且互相平分
【B组】3. （2011江苏南通3分）如同，矩形纸片ABCD中，AB＝2cm，
点E在BC上，且AE＝EC.若将纸片沿AE折叠，点B恰好与AC上的点重合，则AC＝__________cm
4.（2010浙江温州）如 ( http: / / www.21cnjy.com )图，AC；BD是矩形ABCD的对角线，过点D作DE∥AC交BC的延长线于E，则图中与△ABC全等的三角形共有（ ）
A．1个 B．2个 C．3个 D．4个
5.（2011山东泰安，3分）如图，点 ( http: / / www.21cnjy.com )O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为
A.2 B. eq \f(3,2) C. D.6
【C组】6.（2011四川宜宾,7 ( http: / / www.21cnjy.com ),3分）如图，矩形纸片ABCD中，已知AD=8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为（ ）
A．3 B．4 C．5 D．6
7．如图，在矩形ABCD中，BE平分∠ABC，交CD于点E，点F在边BC上，
如果FE⊥AE，求证FE=AE。②如果FE=AE 你能证明FE⊥AE吗？
（提示：①要证FE=AE，只须证明 ( http: / / www.21cnjy.com )△ADE≌△ECF；由矩形的性质知∠C=∠D=90°，及条件BE平分∠ABC，易证△BEC是等腰直角三角形，得到EC=BC，则EC=AD，再由条件FE⊥AE，可以证出另外一组对应角相等。②由前面的证明为启示以小组为单位讨论。）
19.2.1矩形的判定学案
1．(1)【课标考纲解读】
利用矩形的判定进行有关的计算和证明。
(2)【状元学习方案】
经历探索矩形的概念和性质的过程，渗透运动联系，从量变到质变的观点；
2．【学习目标】
知识目标：理解并掌握矩形的判定方法．
能力目标：探索并掌握矩形的判定方法，利用矩形的判定解决问题.
情感目标：让学生在探究过程中加深对矩形的理解，激发他们的求知欲望.
3．【重难点】
教学重点：利用矩形的判定进行推理和证明．
教学难点：证明的严谨性及独立分析和解决问题的培养。
4．【教学方法】
自主合作，交流展示
5．【学习过程】
一、知识链接：
1.矩形是轴对称图形，它有______条对称轴．
2.在矩形ABCD中，对角线AC，BD相交于点O，若对角线AC=10cm，边BC=8cm，则△ABO的周长为________．
3.想一想：矩形有哪些性质？在这些性质中那些是平行四边形所没有的？列表进行比较.
平行四边形 矩形
边
角
对角线
二、学习新知：自学教材95—96页
1、矩形是特殊的平行四边形，怎样判定一个平行四边形是矩形呢 请说出最基本的方法：
________________________________________________________________________________.
矩形具有平行四边形不具有的性质是:________________________________________________.
思考：工人师傅在做门窗或矩 ( http: / / www.21cnjy.com )形零件时，不仅要测量两组对边的长度是否相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形，你能得到矩形一个判定定理吗？
矩形判定方法1：_________________________________________________ 。
你能证明它吗？ 图表画在下面
已知：
求证：
证明：
2.做一做：按照画“边 ( http: / / www.21cnjy.com )——直角、边——直角、边——直角、边”这样四步画出一个四边形.判断它是一个矩形吗 说明理由. （探索得到矩形的另一个判定）
矩形判定方法2：____________________________________________________。
（指出：判定一个四边形是矩形，知道三个角是直角，条件就够了．因为由四边形内角和可知，这时第四个角一定是直角．）
你能证明它吗？
分组讨论，小组展示
3.议一议：下列各句判定矩形的说法是否正确？为什么？
（1）有一个角是直角的四边形是矩形；（ ） （2）有四个角是直角的四边形是矩形；（ ）
（3）四个角都相等的四边形是矩形；（ ） （4）对角线相等的四边形是矩形；（ ）
(5）对角线相等且互相垂直的四边形是矩形；（ ）
（6）对角线互相平分且相等的四边形是矩形；（ ）
（7）对角线相等，且有一个角是直角的四边形是矩形； （ ）
（8）一组邻边垂直，一组对边平行且相等的四边形是矩形；（ ）
（9）两组对边分别平行，且对角线相等的四边形是矩形． ( )
三、例题学习。
例1.：已知□ABCD的对角线AC、B ( http: / / www.21cnjy.com )D相交于点O，△AOB是等边三角形，AB=4 cm，求这个平行四边形的面积．(提示：只要判定出平行四边形ABCD是矩形，易求面积)
( http: / / www.21cnjy.com / )
例2：已知：如图，□ABCD的四个内角 ( http: / / www.21cnjy.com )的平分线分别相交于点E、F、G、H．求证：四边形EFGH是矩形．（提示：由条件易证∠E=∠G=90°，只须再证∠GFE或∠GHE为90°，利用矩形判定2可证）
( http: / / www.21cnjy.com / )
例3：已知：如图，□ABCD中，AC与BD交于O点，∠OAB＝∠OBA．
(1)求证：四边形ABCD为矩形；
(2)作BE⊥AC于E，CF⊥BD于F，求证：BE＝CF．
同步练习：
【A组】1．下列说法正确的是（ ）．
（A）有一组对角是直角的四边形一定是矩形（B）有一组邻角是直角的四边形一定是矩形
（C）对角线互相平分的四边形是矩形 （D）对角互补的平行四边形是矩形
2、满足下列条件（ ）的四边形是矩形。
A．有三个角相等 B.有一个角是直角
C.对角线相等且互相垂直 D.对角线相等且互相平分
【B组】3、已知：如图 ，在△AB ( http: / / www.21cnjy.com )C中，∠C＝90°， CD为中线，延长CD到点E，使得 DE＝CD．连结AE，BE，则四边形ACBE为矩形．（提示：利用矩形判定1证明，四边形ACBE已满足∠ACB为直角，只须证明四边形ACBE为平行四边形即可）
( http: / / www.21cnjy.com / )
4、已知：如图，在平行四边形ABCD中，E为AD中点，BE=CE，求证：四边形ABCD是矩形。
( http: / / www.21cnjy.com / )
【C组】
5. (2011江苏南京，7分)如图，将平行四边形ABCD的边DC延长
到点E，使CE=DC，连接AE，交BC于点F．
⑴求证：△ABF≌△ECF
⑵若∠AFC=2∠D，连接AC、BE．求证：四边形ABEC是矩形．
（提示：由□ABCD性质可知AB与CD平 ( http: / / www.21cnjy.com )行且相等，CD=CE，则CE与AB平行且相等，则四边形ABEC是平行四边形，又∠AFC=2∠D，∠D=∠ABC，则∠AFC=2∠ABC，易证△ABF是等腰三角形，则AF=BF，可证AE=BC。）
六、课堂作业 班级_____________姓名_____________
【A组】1、在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是（ ）．
A．测量对角线是否相互平分 B．测量两组对边是否分别相等
C．测量一组对角是否都为直角 D．测量其中三角形是否都为直角
2、能判断四边形是矩形的条件是（ ）
A、两条对角线互相平分 B、两条对角线相等
C、两条对角线互相平分且相等 D、两条对角线互相垂直。
【B组】3、如图,EB=EC,EA=ED,AD=BC, ∠AEB=∠DEC,证明:四边形ABCD是矩形.
（提示：由条件显然可得△AEB≌△DE ( http: / / www.21cnjy.com )C，得到AB=DC，再有条件AD=BC，两组对边相等的四边形是平行四边形，由全等可知∠EAB=∠EDC，由EA=ED得∠EAD=∠EDC，易得∠BAD=∠CDA=90°，用矩形定义证明）
( http: / / www.21cnjy.com / )
4、已知四边形ABCD中AC⊥ ( http: / / www.21cnjy.com )BD，E、F、G、H分别是AB、BC、CD、DA的中点，求证：四边形EFGH是矩形。(提示:由条件独立完成图形,利用三角形的中位线性质定理进行证明) 图形画在下面
【C组】5.（2009年衡阳市）如图，△ABC中，AB=AC，AD、AE分别是∠BAC和∠BAC和外角的平分线，BE⊥AE．
（1）求证：DA⊥AE；[提示：∠BA ( http: / / www.21cnjy.com )D=∠BAC，∠BAE=∠BAF，则∠BAD+∠BAE =（∠BAC+∠BAF）]
（2）试判断AB与DE是否相等？并证明你的 ( http: / / www.21cnjy.com )结论．（提示：要证明AB与DE相等，本题可证明四边形BEAD是矩形，则由矩形对角线相等可得，利用矩形判定2证明，由（1）知∠DAE=90°，利用等腰三角形的“三线合一”得AD⊥BC，可得∠ADB=90°，又由条件BE⊥AE得∠AEB=90°。）
A′
G
D
B
C
A
C
A
D
E
H
B
A
B
C
D
E
F
O
（第6题图）
B
C
D
E
A
F
A
B
C
D
E
F