人教版(2019)选择性必修第一册 1.6 反冲现象 火箭 课件(共25张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修第一册 1.6 反冲现象 火箭 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-19 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第6节 反冲现象 火箭
1.定义:当一个物体向某一方向射出(或抛出)它的一部分时,这个物体的剩余部分向相反方向运动的现象.
2.特点:
①物体间相互作用突然发生,时间短,作用强。
②系统所受外力一 般不为零,但远远小于内力。
3. 原 理:
遵循动量守恒定律
一、反冲现象
4. 反冲的应用与防止:
灌溉喷水器是利用反冲原理设计的一种自动灌溉装置,转动方向与水的喷射方向相反,水的前进导致管的后退,弯管就旋转起来。
①灌溉喷水
一、反冲现象
水上滑行能让你在水底潜行,并向海豚一般跃出水面,激起层层浪花,它动作如钢铁侠一般带劲!通过喷射装置产生的巨大推动力,可以产生100马力,并将上升高度提升至接近10米甚至更高,让你领略高于一切的海岸新视角!
作者:
一、反冲现象
②水上滑行
【例题】机关枪重8Kg,射出的子弹质量为20g,若子弹的出口速度为1000m/s,则机枪的后退速度vˊ是多大?
【解析】机枪和子弹这一系统动量守
恒,取子弹的速度方向为正方向,由
动量守恒定律得:0=mv -Mvˊ
vˊ = ( m / M ) v
=[(0.02÷8) x 1000]m/s =2.5m/s
一、反冲现象
1.速度的矢量性
对于原来静止的物体,被抛出部分具有速度时,剩余部分的运动方向与被抛出部分必然相反.
新知探究
一、反冲现象
讨论反冲运动应注意的两个问题
2.速度的相对性
在反冲问题中,若给出的速度是物体间的相对速度,应用动量守恒定律列方程时,应将相对速度转化为相对于同一参考系的速度。
我国早在宋代就发明了火箭,在箭杆上捆一个前端封闭的火药筒,火药点燃后生成的燃气以很大的速度向后喷出,火箭由于反冲而向前运动。
新知探究
二、火箭
1.古代火箭
2. 现代火箭
新知探究
二、火箭
现代火箭主要由壳体和燃料组成,壳体是圆筒形的,前端是封闭的尖端,后端有尾喷管,燃料燃烧产生的高温高压燃气从尾喷管迅速喷出,火箭就向前飞去。
M-m
V0
正方向
V=?
m
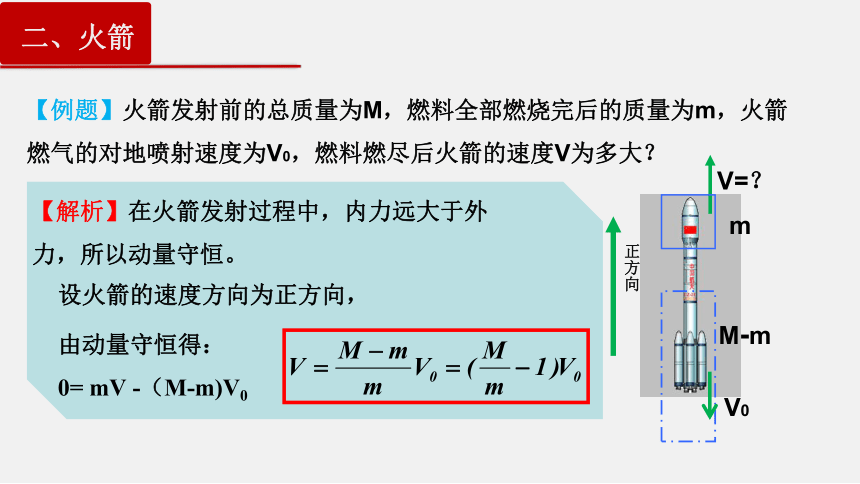
【例题】火箭发射前的总质量为M,燃料全部燃烧完后的质量为m,火箭燃气的对地喷射速度为V0,燃料燃尽后火箭的速度V为多大?
【解析】在火箭发射过程中,内力远大于外力,所以动量守恒。
设火箭的速度方向为正方向,
由动量守恒得:
0= mV -(M-m)V0
新知探究
二、火箭
结论——决定火箭最大飞行速度的因素:
喷气速度
质量比
火箭起飞前的质量
燃料燃尽后的火箭壳质量
新知探究
二、火箭
质量比:火箭开始飞行时的质量与燃料燃尽时的质量之比。
喷气的速度:目前常用的液体燃料是液氢,用液氧做氧化剂,喷气速度在2000m/s到5000m/s
要发射人造卫星,这样的火箭还不能
达到所需的速度.
如何解决卫星发射问题?
新知探究
科学漫步
质量比:火箭的质量比在6~10 左右
火箭在飞行过程中抛掉空壳后,可以使m变得更小,从而使得质量比增大,进而提高火箭最终所能获得的速度。
要提高火箭的速度,需要在减轻火箭本身质量上面下功夫。
苏联科学家齐奥尔科夫斯基提出多级火箭的概念:把火箭一级一级接在一起,第一级燃料用完后把箭体抛弃,减轻负担,然后第二级开始工作,一级一级连续工作,理论上火箭速度可以提的很高。
新知探究
科学漫步
实际应用中一般不会超过4级,因为级数太多时,连接机构和控制机构的质量会增加很多,工作的可靠性也会降低。
运载火箭一般采用液体推进剂,第一、二级多用液氧、煤油或四氧化二氮。末级用液氧、液氢高能推进,称为低温液体火箭,技术比较复杂,目前只有美国、俄斯、法国、中国和日本等少数几个国家掌握低温液体火箭技术.
目前拥有运载火箭的国家有俄罗斯、美国、法国、英国、中国、日本、印度和以色列。当今世界上最大的运载火箭是俄罗斯的“能源”号,它长60米,底部最大直径20米,重3000多吨,能将120吨的有效载荷送入近地轨道。迄今为止运载火箭均为一次使用的,成本高。一次发射,少的几千万美元,多的上亿美元。不能重复使用,资源浪费大。
新知探究
科学漫步
参考系变化:
v人地= v人车 + v车地
注意:上式为矢量式,规定正方向后务必带入相应正负号。
三、动量守恒定律中的相对速度
【例题】总质量为M的火箭以速度v0飞行,质量为m的燃料相对于火箭以速度u向后喷出,则火箭的速度大小为( )
A.v0+mu/M
B.v0-mu/M
C.v0+(v0+u) m/(M-m)
D.v0+mu/(M-m)
【分析】设向前为正方向。燃料相对地速度V1=V-u
2.喷射前后火箭、燃料系统动量守恒
MV0=(M-m)V+m(v-u) , 解得:v= v0+mu/M
【例题】如图所示,装甲车和其中炮弹的总质量为M,正沿轨道向右匀速行驶,其速度为v0,发射一枚质量为m的炮弹后,装甲车的速度变为v,仍向右行驶.若不计轨道的摩擦,求炮弹射出炮口时相对于炮口的速度是多少?(炮管是水平的)
【分析】设相对炮口速度为u,则对地速度为u+v.
动量守恒:MV0=(M-m)v+m(u+v)
则u=M(v0-v)/m
三、动量守恒定律中的相对速度
问题情景:静止在水面上的小船长为L,质量为M,在船的最右端站有一质量为m的人,不计水的阻力,当人从最右端走到最左端的过程中,小船移动的距离是多大?
S2
S1
四、人船模型
【分析】由系统动量守衡:
m v1 = M v2
m v1 t = M v2 t
m s人 = M s船 ---------- ①
s人 + s船 = L ----------②
【拓展应用】载人气球原静止在高度为H的高空,气球的质量为M,人的质量为m,现人要沿气球上的软绳梯滑至地面,则绳梯至少要多长?
H
S
H
【分析】由系统动量守恒:
mv1=Mv2
则 mH=Ms,
且 s+H=L
L=(1+m/M)H
四、人船模型
1.解前画出人、船位移草图;
2.运动情况:人走船行、人停船停;人加速船加速、人减速船减速。
3.原理:动量守恒定律
4.人船速度关系:0=mv1-MV2.则v1/v2=M/m,
任意时刻速度与质量成反比。
5.人船位移关系:
mx1-MX2=0, 则x1/x2=M/m。
x1+x2=L L----船的长度
则:x1=mL/(m+M), x2=ML/(M+m)
v1
v2
x1
x2
L
M
m
人船模型解题思路
课堂小结
遵循动量守恒定律
反冲
静止或运动的物体分离出一部分物体 ,使另一部分向相反方向运动的现象叫反冲运动。
火箭
火箭飞行的原理---利用反冲运动.决定火箭最终飞行速度的因素:喷气速度+质量比
【典例1】(多选)(2022·甘肃·临洮县文峰中学高二阶段练习)一只质量为0.9kg的乌贼吸入0.1kg的水后,静止在水中。遇到危险时,它在极短时间内把吸入的水向后全部喷出,以大小为2m/s的速度向前逃窜。下列说法正确的是( )
A.乌贼喷出的水的速度大小为18m/s
B.在乌贼喷水的过程中,乌贼所受合力的冲量大小为0.9N·s
C.在乌贼喷水的过程中,乌贼和喷出的水组成的系统的动量增大
D.在乌贼喷水的过程中,有18J的生物能转化成机械能
典例分析
【正确答案】AD
【典例2】(2022·广东·佛山市第四中学高二阶段练习)2021年9月17日13时30分,“神舟十二号”返回舱在东风着陆场安全降落。“神舟”系列航天飞船返回舱返回地面的示意图如图所示,其过程可简化为:打开降落伞一段时间后,整个装置沿竖直方向匀速下降,为确保返回舱能安全着陆,在返回舱距地面1m左右时,舱内宇航员主动切断与降落伞的连接(“切伞”),同时点燃返回舱的缓冲火箭,在火箭向下喷气过程中返回舱减至安全速度。已知“切伞”瞬间返回舱的速度大小v1=10m/s,火箭喷出的气体速度大小v2=1082m/s,火箭“喷气”时间极短,喷气完成后返回舱的速度大小v3=2m/s,则喷气完成前、后返回舱的质量比为( )
A.45:44 B.100:99
C.125:124 D.135:134
典例分析
【正确答案】D
【典例3】(2022·重庆南开中学高二期末)西晋史学家陈寿在《三国志》中记载:“置象大船之上,而刻其水痕所至,称物以载之,则校可知矣。”这就是著名的曹冲称象的故事。某同学欲挑战曹冲,利用卷尺测定大船的质量。该同学利用卷尺测出船长为L,然后慢速进入静止的平行于河岸的船的船头,再从船头行走至船尾,之后,慢速下船,测出船后退的距离d与自身的质量m,若忽略一切阻力,则船的质量为( )
A. B. C. D.
典例分析
【正确答案】D
【典例4】2021年5月15日,天问一号着陆巡视器成功着陆于火星,中国首次火星探测任务着陆火星取得圆满成功。携带火星车的着陆器与环绕器分离后,最后阶段利用反推火箭在火星表面实现软着陆,设着陆器总质量为M,极短时间内瞬间喷射的燃气质量是m,为使着陆器经一次瞬间喷射燃气后,其下落的速率从v0减为v,需要瞬间喷出的燃气速率约为( )
A.v0-v B.
C. D.
典例分析
【正确答案】C
【典例5】光滑水平面上放有一上表面光滑、倾角为α的斜面体A,斜面体质量为M、底边长为L,如图所示。将一质量为m、可视为质点的滑块B从斜面的顶端由静止释放,滑块B经过时间t刚好滑到斜面底端,重力加速度为g,则下列说法中正确的是( )
A.滑块B下滑的过程中,A、B组成的系统机械能不守恒,水平方向动量守恒
B.滑块B下滑到斜面体底端时,重力的瞬时功率为
C.滑块下滑过程中,支持力对B做负功
D.此过程中滑块B向右滑动的距离为
典例分析
【正确答案】C
【典例6】如图所示,在光滑水平面上有一小车,小车上固定一竖直杆,总质量为M,杆顶系一长为 l 的轻绳,绳另一端系一质量为m的小球,绳被水平拉直处于静止状态,小球处于最右端。将小球由静止释放,重力加速度为g,求小球摆到最低点时小车向右移动的距离。
【解析】当小球到达最低点时,设小球向左移动的距离为s1,小车向右移动的距离为s2,根据动量守恒有:
ms1=Ms2,s1+s2=l
解得:
水平方向动量守恒
典例分析
第6节 反冲现象 火箭
1.定义:当一个物体向某一方向射出(或抛出)它的一部分时,这个物体的剩余部分向相反方向运动的现象.
2.特点:
①物体间相互作用突然发生,时间短,作用强。
②系统所受外力一 般不为零,但远远小于内力。
3. 原 理:
遵循动量守恒定律
一、反冲现象
4. 反冲的应用与防止:
灌溉喷水器是利用反冲原理设计的一种自动灌溉装置,转动方向与水的喷射方向相反,水的前进导致管的后退,弯管就旋转起来。
①灌溉喷水
一、反冲现象
水上滑行能让你在水底潜行,并向海豚一般跃出水面,激起层层浪花,它动作如钢铁侠一般带劲!通过喷射装置产生的巨大推动力,可以产生100马力,并将上升高度提升至接近10米甚至更高,让你领略高于一切的海岸新视角!
作者:
一、反冲现象
②水上滑行
【例题】机关枪重8Kg,射出的子弹质量为20g,若子弹的出口速度为1000m/s,则机枪的后退速度vˊ是多大?
【解析】机枪和子弹这一系统动量守
恒,取子弹的速度方向为正方向,由
动量守恒定律得:0=mv -Mvˊ
vˊ = ( m / M ) v
=[(0.02÷8) x 1000]m/s =2.5m/s
一、反冲现象
1.速度的矢量性
对于原来静止的物体,被抛出部分具有速度时,剩余部分的运动方向与被抛出部分必然相反.
新知探究
一、反冲现象
讨论反冲运动应注意的两个问题
2.速度的相对性
在反冲问题中,若给出的速度是物体间的相对速度,应用动量守恒定律列方程时,应将相对速度转化为相对于同一参考系的速度。
我国早在宋代就发明了火箭,在箭杆上捆一个前端封闭的火药筒,火药点燃后生成的燃气以很大的速度向后喷出,火箭由于反冲而向前运动。
新知探究
二、火箭
1.古代火箭
2. 现代火箭
新知探究
二、火箭
现代火箭主要由壳体和燃料组成,壳体是圆筒形的,前端是封闭的尖端,后端有尾喷管,燃料燃烧产生的高温高压燃气从尾喷管迅速喷出,火箭就向前飞去。
M-m
V0
正方向
V=?
m
【例题】火箭发射前的总质量为M,燃料全部燃烧完后的质量为m,火箭燃气的对地喷射速度为V0,燃料燃尽后火箭的速度V为多大?
【解析】在火箭发射过程中,内力远大于外力,所以动量守恒。
设火箭的速度方向为正方向,
由动量守恒得:
0= mV -(M-m)V0
新知探究
二、火箭
结论——决定火箭最大飞行速度的因素:
喷气速度
质量比
火箭起飞前的质量
燃料燃尽后的火箭壳质量
新知探究
二、火箭
质量比:火箭开始飞行时的质量与燃料燃尽时的质量之比。
喷气的速度:目前常用的液体燃料是液氢,用液氧做氧化剂,喷气速度在2000m/s到5000m/s
要发射人造卫星,这样的火箭还不能
达到所需的速度.
如何解决卫星发射问题?
新知探究
科学漫步
质量比:火箭的质量比在6~10 左右
火箭在飞行过程中抛掉空壳后,可以使m变得更小,从而使得质量比增大,进而提高火箭最终所能获得的速度。
要提高火箭的速度,需要在减轻火箭本身质量上面下功夫。
苏联科学家齐奥尔科夫斯基提出多级火箭的概念:把火箭一级一级接在一起,第一级燃料用完后把箭体抛弃,减轻负担,然后第二级开始工作,一级一级连续工作,理论上火箭速度可以提的很高。
新知探究
科学漫步
实际应用中一般不会超过4级,因为级数太多时,连接机构和控制机构的质量会增加很多,工作的可靠性也会降低。
运载火箭一般采用液体推进剂,第一、二级多用液氧、煤油或四氧化二氮。末级用液氧、液氢高能推进,称为低温液体火箭,技术比较复杂,目前只有美国、俄斯、法国、中国和日本等少数几个国家掌握低温液体火箭技术.
目前拥有运载火箭的国家有俄罗斯、美国、法国、英国、中国、日本、印度和以色列。当今世界上最大的运载火箭是俄罗斯的“能源”号,它长60米,底部最大直径20米,重3000多吨,能将120吨的有效载荷送入近地轨道。迄今为止运载火箭均为一次使用的,成本高。一次发射,少的几千万美元,多的上亿美元。不能重复使用,资源浪费大。
新知探究
科学漫步
参考系变化:
v人地= v人车 + v车地
注意:上式为矢量式,规定正方向后务必带入相应正负号。
三、动量守恒定律中的相对速度
【例题】总质量为M的火箭以速度v0飞行,质量为m的燃料相对于火箭以速度u向后喷出,则火箭的速度大小为( )
A.v0+mu/M
B.v0-mu/M
C.v0+(v0+u) m/(M-m)
D.v0+mu/(M-m)
【分析】设向前为正方向。燃料相对地速度V1=V-u
2.喷射前后火箭、燃料系统动量守恒
MV0=(M-m)V+m(v-u) , 解得:v= v0+mu/M
【例题】如图所示,装甲车和其中炮弹的总质量为M,正沿轨道向右匀速行驶,其速度为v0,发射一枚质量为m的炮弹后,装甲车的速度变为v,仍向右行驶.若不计轨道的摩擦,求炮弹射出炮口时相对于炮口的速度是多少?(炮管是水平的)
【分析】设相对炮口速度为u,则对地速度为u+v.
动量守恒:MV0=(M-m)v+m(u+v)
则u=M(v0-v)/m
三、动量守恒定律中的相对速度
问题情景:静止在水面上的小船长为L,质量为M,在船的最右端站有一质量为m的人,不计水的阻力,当人从最右端走到最左端的过程中,小船移动的距离是多大?
S2
S1
四、人船模型
【分析】由系统动量守衡:
m v1 = M v2
m v1 t = M v2 t
m s人 = M s船 ---------- ①
s人 + s船 = L ----------②
【拓展应用】载人气球原静止在高度为H的高空,气球的质量为M,人的质量为m,现人要沿气球上的软绳梯滑至地面,则绳梯至少要多长?
H
S
H
【分析】由系统动量守恒:
mv1=Mv2
则 mH=Ms,
且 s+H=L
L=(1+m/M)H
四、人船模型
1.解前画出人、船位移草图;
2.运动情况:人走船行、人停船停;人加速船加速、人减速船减速。
3.原理:动量守恒定律
4.人船速度关系:0=mv1-MV2.则v1/v2=M/m,
任意时刻速度与质量成反比。
5.人船位移关系:
mx1-MX2=0, 则x1/x2=M/m。
x1+x2=L L----船的长度
则:x1=mL/(m+M), x2=ML/(M+m)
v1
v2
x1
x2
L
M
m
人船模型解题思路
课堂小结
遵循动量守恒定律
反冲
静止或运动的物体分离出一部分物体 ,使另一部分向相反方向运动的现象叫反冲运动。
火箭
火箭飞行的原理---利用反冲运动.决定火箭最终飞行速度的因素:喷气速度+质量比
【典例1】(多选)(2022·甘肃·临洮县文峰中学高二阶段练习)一只质量为0.9kg的乌贼吸入0.1kg的水后,静止在水中。遇到危险时,它在极短时间内把吸入的水向后全部喷出,以大小为2m/s的速度向前逃窜。下列说法正确的是( )
A.乌贼喷出的水的速度大小为18m/s
B.在乌贼喷水的过程中,乌贼所受合力的冲量大小为0.9N·s
C.在乌贼喷水的过程中,乌贼和喷出的水组成的系统的动量增大
D.在乌贼喷水的过程中,有18J的生物能转化成机械能
典例分析
【正确答案】AD
【典例2】(2022·广东·佛山市第四中学高二阶段练习)2021年9月17日13时30分,“神舟十二号”返回舱在东风着陆场安全降落。“神舟”系列航天飞船返回舱返回地面的示意图如图所示,其过程可简化为:打开降落伞一段时间后,整个装置沿竖直方向匀速下降,为确保返回舱能安全着陆,在返回舱距地面1m左右时,舱内宇航员主动切断与降落伞的连接(“切伞”),同时点燃返回舱的缓冲火箭,在火箭向下喷气过程中返回舱减至安全速度。已知“切伞”瞬间返回舱的速度大小v1=10m/s,火箭喷出的气体速度大小v2=1082m/s,火箭“喷气”时间极短,喷气完成后返回舱的速度大小v3=2m/s,则喷气完成前、后返回舱的质量比为( )
A.45:44 B.100:99
C.125:124 D.135:134
典例分析
【正确答案】D
【典例3】(2022·重庆南开中学高二期末)西晋史学家陈寿在《三国志》中记载:“置象大船之上,而刻其水痕所至,称物以载之,则校可知矣。”这就是著名的曹冲称象的故事。某同学欲挑战曹冲,利用卷尺测定大船的质量。该同学利用卷尺测出船长为L,然后慢速进入静止的平行于河岸的船的船头,再从船头行走至船尾,之后,慢速下船,测出船后退的距离d与自身的质量m,若忽略一切阻力,则船的质量为( )
A. B. C. D.
典例分析
【正确答案】D
【典例4】2021年5月15日,天问一号着陆巡视器成功着陆于火星,中国首次火星探测任务着陆火星取得圆满成功。携带火星车的着陆器与环绕器分离后,最后阶段利用反推火箭在火星表面实现软着陆,设着陆器总质量为M,极短时间内瞬间喷射的燃气质量是m,为使着陆器经一次瞬间喷射燃气后,其下落的速率从v0减为v,需要瞬间喷出的燃气速率约为( )
A.v0-v B.
C. D.
典例分析
【正确答案】C
【典例5】光滑水平面上放有一上表面光滑、倾角为α的斜面体A,斜面体质量为M、底边长为L,如图所示。将一质量为m、可视为质点的滑块B从斜面的顶端由静止释放,滑块B经过时间t刚好滑到斜面底端,重力加速度为g,则下列说法中正确的是( )
A.滑块B下滑的过程中,A、B组成的系统机械能不守恒,水平方向动量守恒
B.滑块B下滑到斜面体底端时,重力的瞬时功率为
C.滑块下滑过程中,支持力对B做负功
D.此过程中滑块B向右滑动的距离为
典例分析
【正确答案】C
【典例6】如图所示,在光滑水平面上有一小车,小车上固定一竖直杆,总质量为M,杆顶系一长为 l 的轻绳,绳另一端系一质量为m的小球,绳被水平拉直处于静止状态,小球处于最右端。将小球由静止释放,重力加速度为g,求小球摆到最低点时小车向右移动的距离。
【解析】当小球到达最低点时,设小球向左移动的距离为s1,小车向右移动的距离为s2,根据动量守恒有:
ms1=Ms2,s1+s2=l
解得:
水平方向动量守恒
典例分析
