青岛版数学七年级上册 7.1 等式的基本性质 课件(共18张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 7.1 等式的基本性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 640.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-19 21:45:38 | ||
图片预览



文档简介
(共18张PPT)
第7章 一元一次方程
7.1 等式的基本性质
学习目标
探究并掌握等式的基本性质
能够利用等式的基本性质将等式变形
能够利用等式的基本性质解决实际应用问题
b
b
b
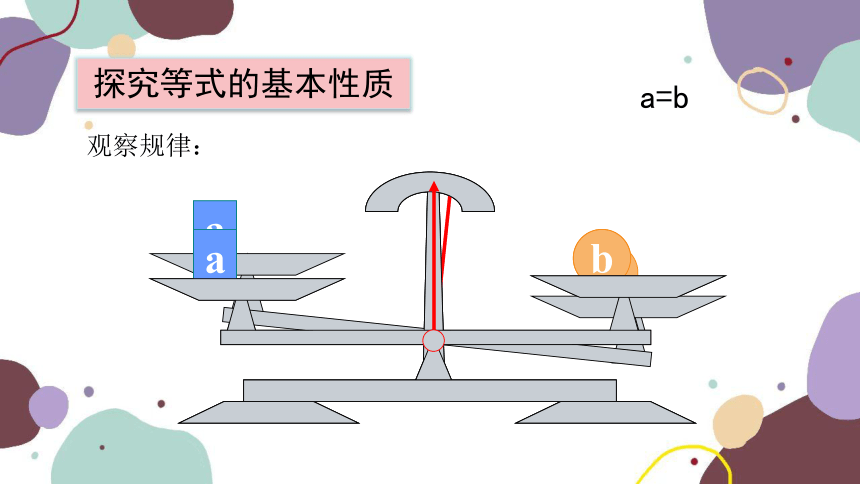
探究等式的基本性质
a
a
a=b
观察规律:
b
1
b
a
1
a
b
1
1
a
1
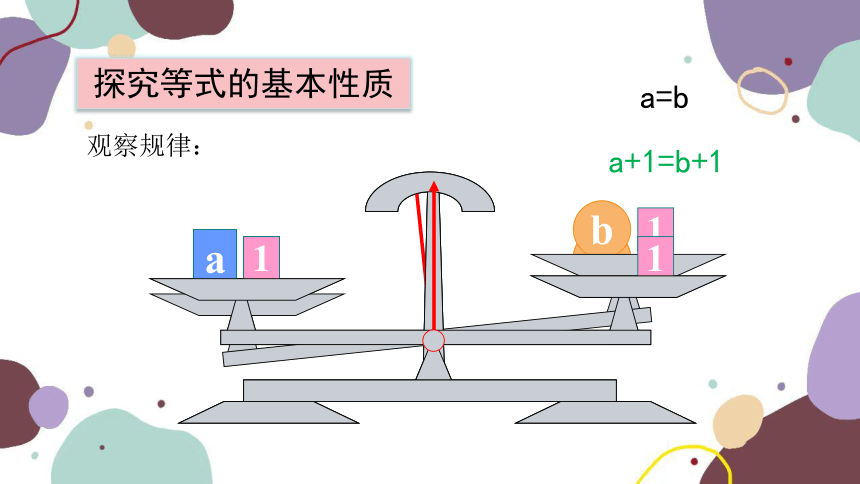
a=b
a+1=b+1
探究等式的基本性质
观察规律:
b
c
b
a
c
a
b
c
c
a
c
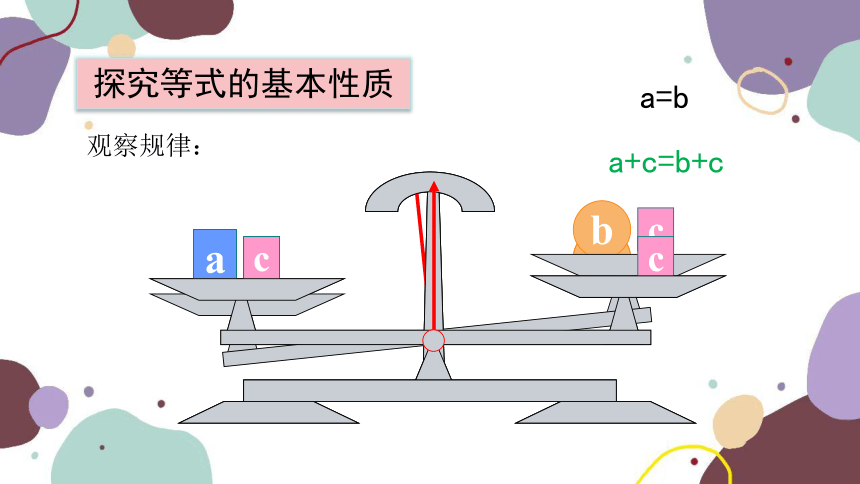
a=b
a+c=b+c
探究等式的基本性质
观察规律:
c
c
c
a
b
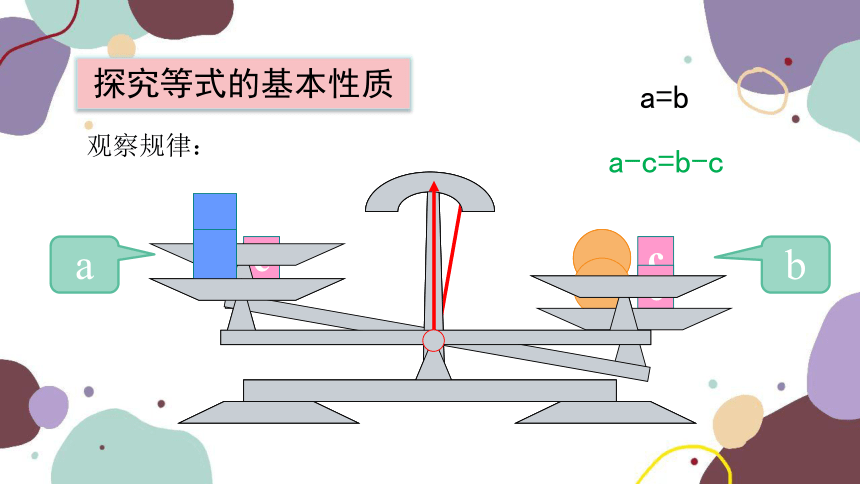
a=b
a-c=b-c
探究等式的基本性质
观察规律:
等式的基本性质
也就是说,等式两边都加上(或减去)同一个整式,所得的结果仍是等式
由此我们得出等式的基本性质1:
如果a=b,那么a+c=b+c,a-c=b-c
探究等式的基本性质
a
b
a
a
a
b
b
a
a
b
b
…
…
b
a
b
a
c个
c个
a=b
ac=bc
等式的基本性质
也就是说,等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式
由此我们得出等式的基本性质2:
如果a=b,那么ac=bc
等式的基本性质
注意等式的基本性质要抓“两同”:
(2)同一个数:等式两边加减和乘的必须是同一个数,除以的必须是同一个不为0的数
(1)同一种运算:等式两边必须都进行同一种运算
等式的其他性质
等式还有对称性和传递性的性质哦!
对称性:等式左、右两边互换位置,所得结果
仍是等式,即如果a=b,那么b=a.
传递性:如果a=b,b=c,那么a=c.
随堂练习
例1 在下列各题的横线上填上适当的整式,使等式成立,并说明根据的是等式的哪一条基本性质以及是怎样变形的.
(1)如果2x-5=3,那么2x=3+______;
(2)如果-x=1,那么x=______
解:
根据等式的基本性质2,两边都除以(或乘)-1
(2)x=-1
根据等式的基本性质1,两边都加上5
(1)2x=3+5
随堂练习
解:
根据等式的基本性质1,等式两边同时减5,得3x=8-5.
(1)不正确.
(2)不正确.
随堂练习
如图,天平中的物体A,B,C(假设物体A,B,C 的质量分别为a,b,c)使天平处于平衡状态,则物体A与物体C的质量关系是( )
A
A
B
B
B
B
B
C
C
C
A.2a=3c B.4a=9c C.a=2c D.a=c
B
随堂练习
解析:
所以4a=6b=9c,即4a=9c.
所以4a=6b,6b=9c,
由图可知,2a=3b,2b=3c,
A
A
B
B
B
B
B
C
C
C
故选B.
总结
等式两边都加上(或减去)同一个整式,所得的结果仍是等式
等式的基本性质1:
如果a=b,那么a+c=b+c,a-c=b-c
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式
等式的基本性质2:
如果a=b,那么ac=bc
巩固练习
1.由0.3y=6,得y=20,其变形过程是( )
A.等式两边都加上0.3
B.等式两边都减去0.3
C.等式两边都乘0.3
D.等式两边都除以0.3
D
巩固练习
2.利用等式的基本性质,在横线上填上适当的数或式子,并说明变形的根据以及是怎样变形的.
(1)如果2x-3=-5,那么2x=_____,x=_____;
(2)如果5x+2=2x-4,那么3x=_____,x=_____.
解:
-2
-1
-6
-2
再根据等式的基本性质2,两边同时除以2,得x=-1.
(1)根据等式的基本性质1,等式两边同时加3,得2x=-2;
再根据等式的基本性质2,两边同时除以3,得x=-2.
(2)根据等式的基本性质1,等式两边同时减2x+2,得3x=-6;
第7章 一元一次方程
7.1 等式的基本性质
学习目标
探究并掌握等式的基本性质
能够利用等式的基本性质将等式变形
能够利用等式的基本性质解决实际应用问题
b
b
b
探究等式的基本性质
a
a
a=b
观察规律:
b
1
b
a
1
a
b
1
1
a
1
a=b
a+1=b+1
探究等式的基本性质
观察规律:
b
c
b
a
c
a
b
c
c
a
c
a=b
a+c=b+c
探究等式的基本性质
观察规律:
c
c
c
a
b
a=b
a-c=b-c
探究等式的基本性质
观察规律:
等式的基本性质
也就是说,等式两边都加上(或减去)同一个整式,所得的结果仍是等式
由此我们得出等式的基本性质1:
如果a=b,那么a+c=b+c,a-c=b-c
探究等式的基本性质
a
b
a
a
a
b
b
a
a
b
b
…
…
b
a
b
a
c个
c个
a=b
ac=bc
等式的基本性质
也就是说,等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式
由此我们得出等式的基本性质2:
如果a=b,那么ac=bc
等式的基本性质
注意等式的基本性质要抓“两同”:
(2)同一个数:等式两边加减和乘的必须是同一个数,除以的必须是同一个不为0的数
(1)同一种运算:等式两边必须都进行同一种运算
等式的其他性质
等式还有对称性和传递性的性质哦!
对称性:等式左、右两边互换位置,所得结果
仍是等式,即如果a=b,那么b=a.
传递性:如果a=b,b=c,那么a=c.
随堂练习
例1 在下列各题的横线上填上适当的整式,使等式成立,并说明根据的是等式的哪一条基本性质以及是怎样变形的.
(1)如果2x-5=3,那么2x=3+______;
(2)如果-x=1,那么x=______
解:
根据等式的基本性质2,两边都除以(或乘)-1
(2)x=-1
根据等式的基本性质1,两边都加上5
(1)2x=3+5
随堂练习
解:
根据等式的基本性质1,等式两边同时减5,得3x=8-5.
(1)不正确.
(2)不正确.
随堂练习
如图,天平中的物体A,B,C(假设物体A,B,C 的质量分别为a,b,c)使天平处于平衡状态,则物体A与物体C的质量关系是( )
A
A
B
B
B
B
B
C
C
C
A.2a=3c B.4a=9c C.a=2c D.a=c
B
随堂练习
解析:
所以4a=6b=9c,即4a=9c.
所以4a=6b,6b=9c,
由图可知,2a=3b,2b=3c,
A
A
B
B
B
B
B
C
C
C
故选B.
总结
等式两边都加上(或减去)同一个整式,所得的结果仍是等式
等式的基本性质1:
如果a=b,那么a+c=b+c,a-c=b-c
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式
等式的基本性质2:
如果a=b,那么ac=bc
巩固练习
1.由0.3y=6,得y=20,其变形过程是( )
A.等式两边都加上0.3
B.等式两边都减去0.3
C.等式两边都乘0.3
D.等式两边都除以0.3
D
巩固练习
2.利用等式的基本性质,在横线上填上适当的数或式子,并说明变形的根据以及是怎样变形的.
(1)如果2x-3=-5,那么2x=_____,x=_____;
(2)如果5x+2=2x-4,那么3x=_____,x=_____.
解:
-2
-1
-6
-2
再根据等式的基本性质2,两边同时除以2,得x=-1.
(1)根据等式的基本性质1,等式两边同时加3,得2x=-2;
再根据等式的基本性质2,两边同时除以3,得x=-2.
(2)根据等式的基本性质1,等式两边同时减2x+2,得3x=-6;
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
