11.3.2 多边形的内角和 课件(共35张PPT)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.3.2 多边形的内角和 课件(共35张PPT)2023-2024学年人教版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-20 18:09:23 | ||
图片预览






文档简介
(共35张PPT)
第十一章 三角形
11.3 多边形及其内角和
11.3.2 多边形的内角和
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.掌握多边形内角和与外角和公式.
2.能通过不同方法探索多边形的内角和与外角和公式.(难点)
3.能灵活运用多边形的内角和与外角和公式解决问题.(重点)
新课导入
复习引入
什么是多边形的内角?什么是多边形的外角?
多边形相邻两边组成的角叫做多边形的内角.
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
多边形的内角和与外角和有什么性质呢?
新知探究
知识点1 多边形的内角和
(2)长方形和正方形的内角和是多少度?
思考 (1)三角形内角和是多少度?
三角形内角和是180°.
都是360°.
新知探究
知识点1 多边形的内角和
用量角器量出四个内角的大小,发现四边形的四个内角和为360°.
(3)请大家任意画一个四边形,这个四边形的内角和是多少度?是否与长方形和正方形的内角和相等?你是怎么得到内角和的度数的?
但是测量有误差,推理证明更有说服力.
该如何证明呢?
新知探究
知识点1 多边形的内角和
如图,求四边形ABCD的内角和.
C
B
D
分析:如果四边形内角和是360°,我们已经知道三角形内角和是180°,利用三角形内角和定理来证明任意一个四边形的内角和为360°,
可将四边形分成两个三角形.
A
新知探究
知识点1 多边形的内角和
C
B
D
∴∠D+∠DAB+∠B+∠BCD=∠D+(∠2+∠1)+∠B+(∠3+∠4)=(∠D+∠2+∠4)+(∠B+∠1+∠3)=360°,即四边形ABCD的内角和为360°.
1
4
3
2
解:如图,连接对角线AC,则四边形被分为
△ABC和△ACD,
在△ACD中,∠D+∠2+∠4=180°,
在△ABC中,∠B+∠1+∠3=180°.
A
新知探究
知识点1 多边形的内角和
类比四边形内角和的推导方法,请尝试探究五边形和六边形的内角和.
从五边形的一个顶点出发,可以作出 条对角线,它们将五边形分成了 个三角形,五边形的内角和等于180°× .
从六边形的一个顶点出发,可以作出 条对角线,它们将六边形分成了 个三角形,六边形的内角和等于180°× .
2
3
3
3
4
4
新知探究
知识点1 多边形的内角和
多边形的边数 从多边形的一顶点引出的对角线条数 分割出的三角形的个数 多边形内角和
3 0 1 1×180°=180°
4 1 2 2×180°=360°
5 2 3 3×180°=540°
6 3 4 4×180°=720°
...... ...... ...... ......
n
你发现了多边形的内角
和与边数的关系了吗?
n-3
n-2
(n-2)×180°
新知探究
知识点1 多边形的内角和
通过以上的探究,我们发现:从n边形的一个顶点出发,可以作出(n-3)条对角线,它们将n边形分成了(n-2)个三角形,n边形的内角和等于(n-2)×180°.
多边形的内角和公式:n边形的内角和等于(n-2)×180°.
新知探究
知识点1 多边形的内角和
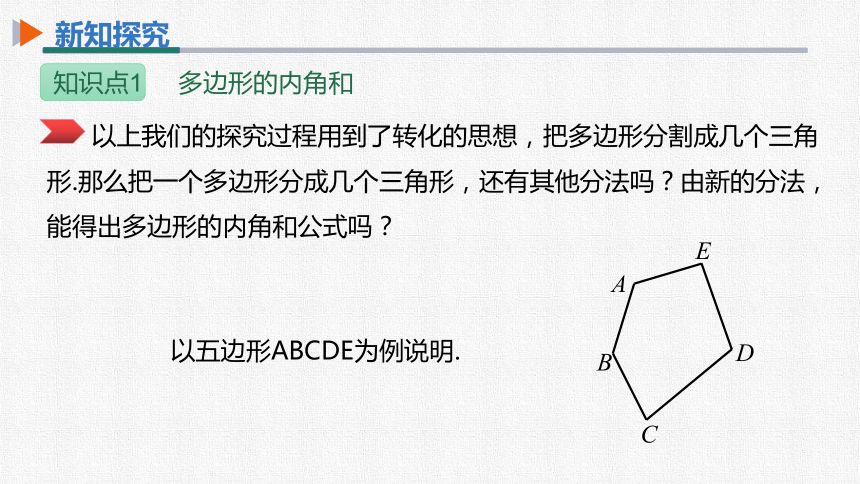
以上我们的探究过程用到了转化的思想,把多边形分割成几个三角形.那么把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边形的内角和公式吗?
A
C
D
E
B
以五边形ABCDE为例说明.
新知探究
知识点1 多边形的内角和
A
C
D
E
B
F
A
C
D
E
B
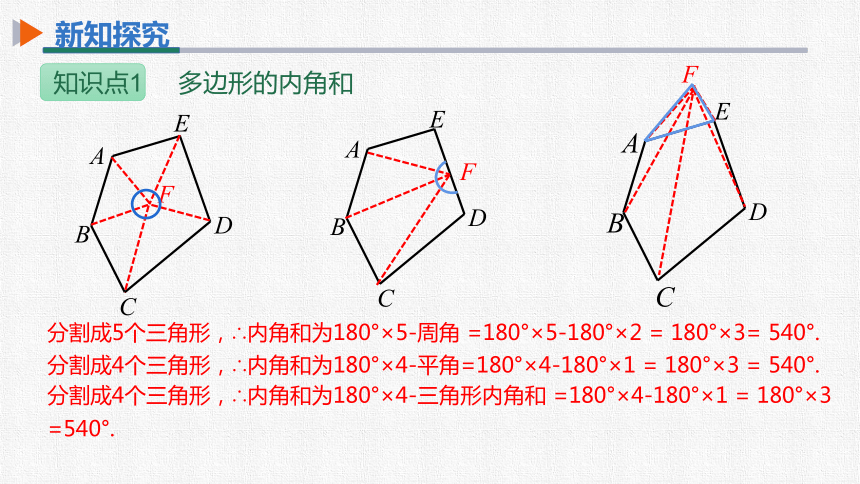
分割成5个三角形,∴内角和为180°×5-周角 =180°×5-180°×2 = 180°×3= 540°.
A
C
D
E
B
F
F
分割成4个三角形,∴内角和为180°×4-平角=180°×4-180°×1 = 180°×3 = 540°.
分割成4个三角形,∴内角和为180°×4-三角形内角和 =180°×4-180°×1 = 180°×3
=540°.
新知探究
知识点1 多边形的内角和
外部
多边形分割成三角形
内部
边
顶点
分割点位置
转化思想
新知探究
知识点1 多边形的内角和
例1 如果一个四边形的一组对角互补,那么另外一组对角有什么关系?
B
A
C
D
解:如图,若在四边形ABCD中,∠A和∠C互补,
则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360 °-(∠A+∠C)=180°.
如果一个四边形的一组对角互补,那么另外一组对角也互补.
新知探究
知识点1 多边形的内角和
知道了多边形的内角和公式,那么回想正多边形的性质,你知道正多边形的每个内角是多少度吗?为什么?
因为正多边形的每个内角相等,所以用内角和除以内角的个数(n)即可得到正多边形每个内角的度数.
正多边形的每个内角的度数等于 .
跟踪训练
新知探究
1.将一个多边形的边数增加1,它的内角和将( )
A.增加90° B.增加180° C.增加360° D.保持不变
【解析】设原多边形边数是n,则n边形的内角和是(n-2) 180°,边数增加1后,新多边形的内角和是(n+1-2) 180°.∵(n+1-2) 180°-(n-2) 180°=180°.∴它的内角和增加180°.故选B.
由此可以看出,多边形每增加一条边,其内角和就会增加180°.
B
跟踪训练
新知探究
2.(2021春 娄底期中)一个正多边形的内角和为1800°,求它的边数和
每个内角的度数.
解:设这个正多边形的边数是n,则(n-2) 180°=1800°.
解得n=12.
1800°÷12=150°.
故这个正多边形的边数为12;每个内角的度数150°.
利用内角和公式计算时,先不要去括
号,把(n-2)看成一个整体,先求
(n-2)的值,再求n的值.这样可使
运算更简单
知识点2 多边形的外角和
新知探究
分析:
(1)任何一个外角同与它相邻的内角有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
任意一个外角加上与它相邻的内角等于180°.
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
知识点2 多边形的外角和
新知探究
分析:
(2)六边形的6个外角加上与它们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和、外角和有什么关系?
1个外角加上与它相邻的内角等于180°,所以6个外角加上与它们相邻的内角等于180°×6.
上述总和(即六边形的内角和加外角和)为180°×6,六边形的内角和为180°×4,则六边形的外角和为180°×6-180°×4=360°.
知识点2 多边形的外角和
新知探究
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形
的外角和.n边形的外角和又是多少呢?
n个外角加上与它们相邻的内角为180°×n,
n边形的内角和为180°×(n-2),
n边形的外角和为180°×n-180°×(n-2)=360°.
多边形的外角和等于360°.
多边形的外角和为定值,与边数无关
知识点2 多边形的外角和
新知探究
我们也可以像以下这样理解为什么多边形的外角和等于360°.
A
从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向,在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和就等于一个周角,所以多边形的外角和等于360°.
新知探究
知识点1 多边形的内角和
知道了多边形的外角和公式,那么回想正多边形的性质,你知道正多边形的每个外角是多少度吗?为什么?
因为正多边形的每个外角相等,所以用外角和(360°)除以内角的个数(n)即可得到正多边形每个外角的度数.
正多边形的每个外角的度数等于 .
(2021 盐城)若一个多边形的每个外角均为40°,则这个多边形的边数为 .
跟踪训练
新知探究
9
【解析】∵一个多边形的每一个外角均为40°,且多边形的外角和等于360°,∴这个多边形的边数是360°÷40°=9.
课堂小结
多边形的
内角和
内角和计算公式
外角和
正多边形
(n-2)×180°(n为≥3的整数)
多边形的外角和等于360°(与边数无关)
每个内角= ,每个外角=
1.(2020秋 张店区期末)内角和为720°的多边形是( )
A. B. C. D.
课堂训练
【解析】 设多边形为n边形,
依题意有(n-2) 180°=720°,
解得n=6.
该多边形为六边形,故选D.
D
2.(2021扬州模拟)若某多边形的边数增加1,则这个多边形的外角和( )
A.增加180° B.增加360°
C.减少180° D.不变
D
【解析】任意多边形的外角和都是360°,与它的边数无关.
课堂训练
课堂训练
3.(2021春 西湖区校级期中)在四边形ABCD中,∠A+∠C=160°,∠B比∠D大60°,则∠B的度数为( )
A.70° B.80° C.120° D.130°
【解析】 ∵∠A+∠B+∠C+∠D=360°,∠A+∠C=160°,
∴∠B+∠D=200°.∵∠B-∠D=60°,∴2∠B=260°.
解得∠B=130°.故选D.
D
课堂训练
4.(2021广州一模)如图,小明从A点出发,沿直线前进6米后向左转45°,再沿直线前进6米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )米.
A.60 B.72 C.48 D.36
【解析】 根据题意可知,他需要转360÷45=8次才会回到原点,
所以一共走了8×6=48(米).
故选C.
C
课堂训练
5.(2021上海徐汇区二模)如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是( )
A.180° B.270° C.360° D.540°
【解析】一个多边形剪掉一个角后,边数可能减1,可能不变,也可能加1,∴新多边形的边数可能是3,4,5.
∴内角和分别为(3-2)×180°=180°;(4-2)×180°=360°;
(5-2)×180°=540°.∴所得多边形内角和的度数可能是180°,360°,540°,不可能是270°.故选B.
B
课堂训练
6.(2021北京通州区一模)如图中的平面图形由多条直线组成,计算∠1+∠2+∠3+∠4+∠5= °.
360
课堂训练
7.一个多边形的边数由5增加到11,则内角和增加的度数是 °.
方法二:多边形的边数由5增加到11,边数增加了6,.∵多边形每增加一条边,其内角和就会增加180°.∴内角和增加的度数是6×180°=1080°.故答案为1080°.
1080
【解析】方法一:五边形的内角和为(5-2)×180°=540°,十一边形的内角和为(11-2)×180°=1620°.∴内角和增加的度数是1620°-540°=1080°.故答案为1080°.
课堂训练
8.(2021南京一模)如图,五边形ABCDE是正五边形,过点B作AB的垂线交CD于点F,则∠C-∠1= °.
54
【解析】∵五边形ABCDE是正五边形,
∴∠A=∠ABC=∠C=∠D=∠E= =108°.
∵BF⊥AB,∴∠ABF=90°.
∴∠CBF=∠ABC-∠ABF=108°-90°=18°.
∴∠1=180°-∠C-∠CBF=180°-108°-18°=54°.
∴∠C-∠1=108°-54°=54°.故答案为54.
课堂训练
9.已知正多边形的一个内角为144°,求该正多边形的内角和.
解:根据题意,得(n-2)×180°=144°n,
解得n=10.
∴这个正多边形的边数是10.
∴该正多边形的内角和为(10-2)×180°=14400°.
你还有其他解法吗?
课堂训练
解法二:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数= =10.
∴这个正多边形的边数是10.
∴该正多边形的内角和为(10-2)×180°=14400°.
课堂训练
10.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和
=540°.
8
9
不规则图形求角度之和,关键是转化,借助辅助线转化角的关系是常见的思路
解:如图,
第十一章 三角形
11.3 多边形及其内角和
11.3.2 多边形的内角和
学习目标-新课导入-新知探究-课堂小结-课堂训练
学习目标
1.掌握多边形内角和与外角和公式.
2.能通过不同方法探索多边形的内角和与外角和公式.(难点)
3.能灵活运用多边形的内角和与外角和公式解决问题.(重点)
新课导入
复习引入
什么是多边形的内角?什么是多边形的外角?
多边形相邻两边组成的角叫做多边形的内角.
多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
多边形的内角和与外角和有什么性质呢?
新知探究
知识点1 多边形的内角和
(2)长方形和正方形的内角和是多少度?
思考 (1)三角形内角和是多少度?
三角形内角和是180°.
都是360°.
新知探究
知识点1 多边形的内角和
用量角器量出四个内角的大小,发现四边形的四个内角和为360°.
(3)请大家任意画一个四边形,这个四边形的内角和是多少度?是否与长方形和正方形的内角和相等?你是怎么得到内角和的度数的?
但是测量有误差,推理证明更有说服力.
该如何证明呢?
新知探究
知识点1 多边形的内角和
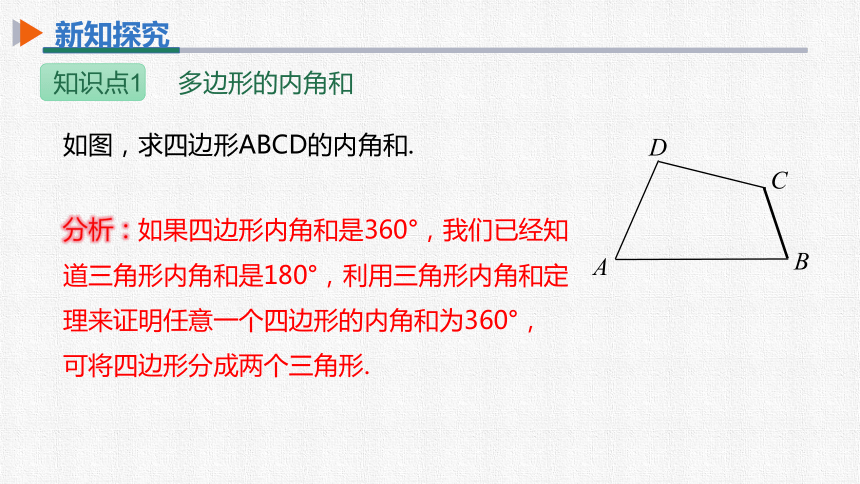
如图,求四边形ABCD的内角和.
C
B
D
分析:如果四边形内角和是360°,我们已经知道三角形内角和是180°,利用三角形内角和定理来证明任意一个四边形的内角和为360°,
可将四边形分成两个三角形.
A
新知探究
知识点1 多边形的内角和
C
B
D
∴∠D+∠DAB+∠B+∠BCD=∠D+(∠2+∠1)+∠B+(∠3+∠4)=(∠D+∠2+∠4)+(∠B+∠1+∠3)=360°,即四边形ABCD的内角和为360°.
1
4
3
2
解:如图,连接对角线AC,则四边形被分为
△ABC和△ACD,
在△ACD中,∠D+∠2+∠4=180°,
在△ABC中,∠B+∠1+∠3=180°.
A
新知探究
知识点1 多边形的内角和
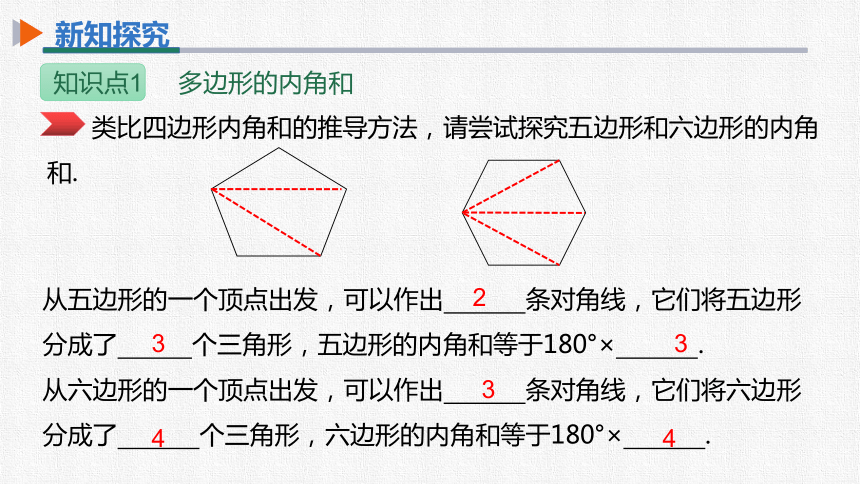
类比四边形内角和的推导方法,请尝试探究五边形和六边形的内角和.
从五边形的一个顶点出发,可以作出 条对角线,它们将五边形分成了 个三角形,五边形的内角和等于180°× .
从六边形的一个顶点出发,可以作出 条对角线,它们将六边形分成了 个三角形,六边形的内角和等于180°× .
2
3
3
3
4
4
新知探究
知识点1 多边形的内角和
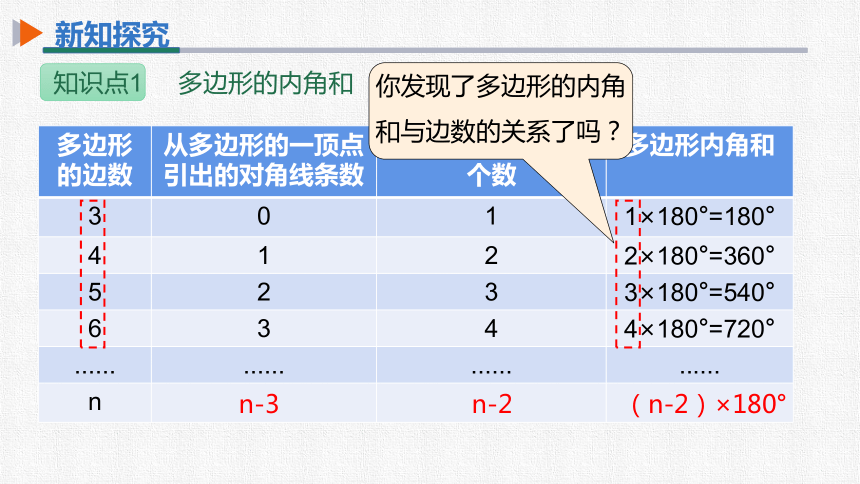
多边形的边数 从多边形的一顶点引出的对角线条数 分割出的三角形的个数 多边形内角和
3 0 1 1×180°=180°
4 1 2 2×180°=360°
5 2 3 3×180°=540°
6 3 4 4×180°=720°
...... ...... ...... ......
n
你发现了多边形的内角
和与边数的关系了吗?
n-3
n-2
(n-2)×180°
新知探究
知识点1 多边形的内角和
通过以上的探究,我们发现:从n边形的一个顶点出发,可以作出(n-3)条对角线,它们将n边形分成了(n-2)个三角形,n边形的内角和等于(n-2)×180°.
多边形的内角和公式:n边形的内角和等于(n-2)×180°.
新知探究
知识点1 多边形的内角和
以上我们的探究过程用到了转化的思想,把多边形分割成几个三角形.那么把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边形的内角和公式吗?
A
C
D
E
B
以五边形ABCDE为例说明.
新知探究
知识点1 多边形的内角和
A
C
D
E
B
F
A
C
D
E
B
分割成5个三角形,∴内角和为180°×5-周角 =180°×5-180°×2 = 180°×3= 540°.
A
C
D
E
B
F
F
分割成4个三角形,∴内角和为180°×4-平角=180°×4-180°×1 = 180°×3 = 540°.
分割成4个三角形,∴内角和为180°×4-三角形内角和 =180°×4-180°×1 = 180°×3
=540°.
新知探究
知识点1 多边形的内角和
外部
多边形分割成三角形
内部
边
顶点
分割点位置
转化思想
新知探究
知识点1 多边形的内角和
例1 如果一个四边形的一组对角互补,那么另外一组对角有什么关系?
B
A
C
D
解:如图,若在四边形ABCD中,∠A和∠C互补,
则∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=360°,
∴∠B+∠D=360 °-(∠A+∠C)=180°.
如果一个四边形的一组对角互补,那么另外一组对角也互补.
新知探究
知识点1 多边形的内角和
知道了多边形的内角和公式,那么回想正多边形的性质,你知道正多边形的每个内角是多少度吗?为什么?
因为正多边形的每个内角相等,所以用内角和除以内角的个数(n)即可得到正多边形每个内角的度数.
正多边形的每个内角的度数等于 .
跟踪训练
新知探究
1.将一个多边形的边数增加1,它的内角和将( )
A.增加90° B.增加180° C.增加360° D.保持不变
【解析】设原多边形边数是n,则n边形的内角和是(n-2) 180°,边数增加1后,新多边形的内角和是(n+1-2) 180°.∵(n+1-2) 180°-(n-2) 180°=180°.∴它的内角和增加180°.故选B.
由此可以看出,多边形每增加一条边,其内角和就会增加180°.
B
跟踪训练
新知探究
2.(2021春 娄底期中)一个正多边形的内角和为1800°,求它的边数和
每个内角的度数.
解:设这个正多边形的边数是n,则(n-2) 180°=1800°.
解得n=12.
1800°÷12=150°.
故这个正多边形的边数为12;每个内角的度数150°.
利用内角和公式计算时,先不要去括
号,把(n-2)看成一个整体,先求
(n-2)的值,再求n的值.这样可使
运算更简单
知识点2 多边形的外角和
新知探究
分析:
(1)任何一个外角同与它相邻的内角有什么关系?
A
B
C
D
E
F
1
2
3
5
4
6
任意一个外角加上与它相邻的内角等于180°.
例2 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和,六边形的外角和等于多少?
知识点2 多边形的外角和
新知探究
分析:
(2)六边形的6个外角加上与它们相邻的内角,所得总和是多少?
(3)上述总和与六边形的内角和、外角和有什么关系?
1个外角加上与它相邻的内角等于180°,所以6个外角加上与它们相邻的内角等于180°×6.
上述总和(即六边形的内角和加外角和)为180°×6,六边形的内角和为180°×4,则六边形的外角和为180°×6-180°×4=360°.
知识点2 多边形的外角和
新知探究
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形
的外角和.n边形的外角和又是多少呢?
n个外角加上与它们相邻的内角为180°×n,
n边形的内角和为180°×(n-2),
n边形的外角和为180°×n-180°×(n-2)=360°.
多边形的外角和等于360°.
多边形的外角和为定值,与边数无关
知识点2 多边形的外角和
新知探究
我们也可以像以下这样理解为什么多边形的外角和等于360°.
A
从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向,在行程中所转的各个角的和,就是多边形的外角和. 由于走了一周,所转的各个角的和就等于一个周角,所以多边形的外角和等于360°.
新知探究
知识点1 多边形的内角和
知道了多边形的外角和公式,那么回想正多边形的性质,你知道正多边形的每个外角是多少度吗?为什么?
因为正多边形的每个外角相等,所以用外角和(360°)除以内角的个数(n)即可得到正多边形每个外角的度数.
正多边形的每个外角的度数等于 .
(2021 盐城)若一个多边形的每个外角均为40°,则这个多边形的边数为 .
跟踪训练
新知探究
9
【解析】∵一个多边形的每一个外角均为40°,且多边形的外角和等于360°,∴这个多边形的边数是360°÷40°=9.
课堂小结
多边形的
内角和
内角和计算公式
外角和
正多边形
(n-2)×180°(n为≥3的整数)
多边形的外角和等于360°(与边数无关)
每个内角= ,每个外角=
1.(2020秋 张店区期末)内角和为720°的多边形是( )
A. B. C. D.
课堂训练
【解析】 设多边形为n边形,
依题意有(n-2) 180°=720°,
解得n=6.
该多边形为六边形,故选D.
D
2.(2021扬州模拟)若某多边形的边数增加1,则这个多边形的外角和( )
A.增加180° B.增加360°
C.减少180° D.不变
D
【解析】任意多边形的外角和都是360°,与它的边数无关.
课堂训练
课堂训练
3.(2021春 西湖区校级期中)在四边形ABCD中,∠A+∠C=160°,∠B比∠D大60°,则∠B的度数为( )
A.70° B.80° C.120° D.130°
【解析】 ∵∠A+∠B+∠C+∠D=360°,∠A+∠C=160°,
∴∠B+∠D=200°.∵∠B-∠D=60°,∴2∠B=260°.
解得∠B=130°.故选D.
D
课堂训练
4.(2021广州一模)如图,小明从A点出发,沿直线前进6米后向左转45°,再沿直线前进6米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )米.
A.60 B.72 C.48 D.36
【解析】 根据题意可知,他需要转360÷45=8次才会回到原点,
所以一共走了8×6=48(米).
故选C.
C
课堂训练
5.(2021上海徐汇区二模)如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是( )
A.180° B.270° C.360° D.540°
【解析】一个多边形剪掉一个角后,边数可能减1,可能不变,也可能加1,∴新多边形的边数可能是3,4,5.
∴内角和分别为(3-2)×180°=180°;(4-2)×180°=360°;
(5-2)×180°=540°.∴所得多边形内角和的度数可能是180°,360°,540°,不可能是270°.故选B.
B
课堂训练
6.(2021北京通州区一模)如图中的平面图形由多条直线组成,计算∠1+∠2+∠3+∠4+∠5= °.
360
课堂训练
7.一个多边形的边数由5增加到11,则内角和增加的度数是 °.
方法二:多边形的边数由5增加到11,边数增加了6,.∵多边形每增加一条边,其内角和就会增加180°.∴内角和增加的度数是6×180°=1080°.故答案为1080°.
1080
【解析】方法一:五边形的内角和为(5-2)×180°=540°,十一边形的内角和为(11-2)×180°=1620°.∴内角和增加的度数是1620°-540°=1080°.故答案为1080°.
课堂训练
8.(2021南京一模)如图,五边形ABCDE是正五边形,过点B作AB的垂线交CD于点F,则∠C-∠1= °.
54
【解析】∵五边形ABCDE是正五边形,
∴∠A=∠ABC=∠C=∠D=∠E= =108°.
∵BF⊥AB,∴∠ABF=90°.
∴∠CBF=∠ABC-∠ABF=108°-90°=18°.
∴∠1=180°-∠C-∠CBF=180°-108°-18°=54°.
∴∠C-∠1=108°-54°=54°.故答案为54.
课堂训练
9.已知正多边形的一个内角为144°,求该正多边形的内角和.
解:根据题意,得(n-2)×180°=144°n,
解得n=10.
∴这个正多边形的边数是10.
∴该正多边形的内角和为(10-2)×180°=14400°.
你还有其他解法吗?
课堂训练
解法二:∵正多边形的一个内角是144°,
∴该正多边形的一个外角为36°,
∵多边形的外角之和为360°,
∴边数= =10.
∴这个正多边形的边数是10.
∴该正多边形的内角和为(10-2)×180°=14400°.
课堂训练
10.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
∵∠3+∠4=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7
=∠1+∠2+∠8+∠9+∠5+∠6+∠7
=五边形的内角和
=540°.
8
9
不规则图形求角度之和,关键是转化,借助辅助线转化角的关系是常见的思路
解:如图,
