2022-2023学年华东师大版七年级数学下册《第9章 多边形》期末综合复习训练题(含解析)
文档属性
| 名称 | 2022-2023学年华东师大版七年级数学下册《第9章 多边形》期末综合复习训练题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 635.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-20 18:19:23 | ||
图片预览



文档简介
七年级数学下册《第9章 多边形》期末综合复习训练题
一、单选题
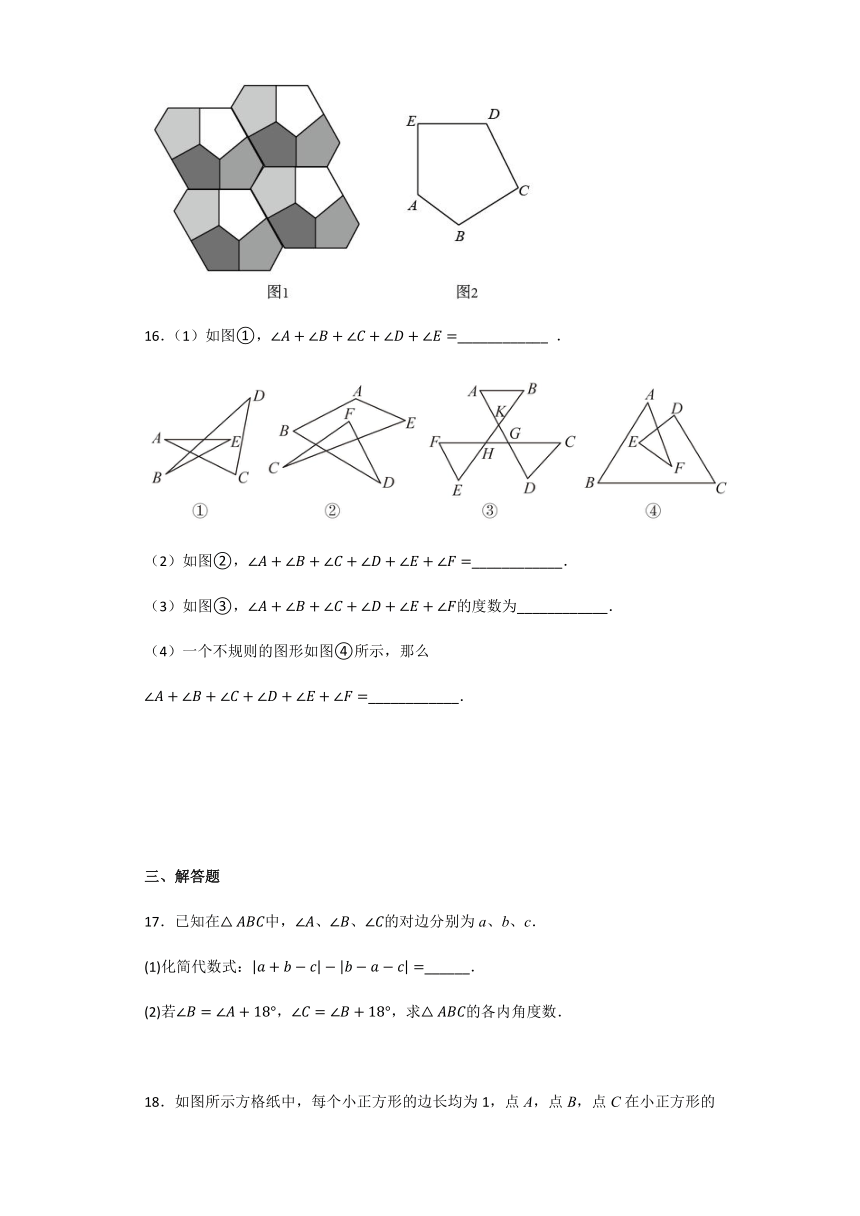
1.下列长度的三条线段,能组成三角形的是( )
A.3,4,7 B.5,6,10 C.2,3,6 D.5,6,11
2.下面四个图形中,线段是的高的图形是( )
A. B.
C. D.
3.下列图形中,具有稳定性的是( )
A. B. C. D.
4.一块四边形玻璃被打破,如图所示.小红想制做一模一样的玻璃,经测量,,则的度数( )
A. B. C. D.
5.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A.12 B.13 C.14 D.15
6.如图,已知在中,是的角平分线,是边上的高,,,求的度数为( )
A. B. C. D.
7.正六边形和下列边长相同的正多边形地砖组合中,能铺满地面的是( )
A.正方形 B.正八边形
C.正十二边形 D.正四边形和正十二边形
8.如图已知是的中线,是的中线,若的面积为20,则的面积为( )
A.5 B.10 C.15 D.18
二、填空题
9.一个多边形的内角和与外角和的差为,则它的边数为______.
10.如图,在中,,,和分别是它的高和角平分线,则________.
11.如图,已知,若,则的度数为_____.
12.正五边形和正方形位置如图所示,连接,则的度数为______.
13.如图,四边形中,,若沿图中虚线剪去,则________.
14.如图,、的平分线交于,;、的平分线交于,;如此下去,、的平分线的交角为;…若,,则为________度.
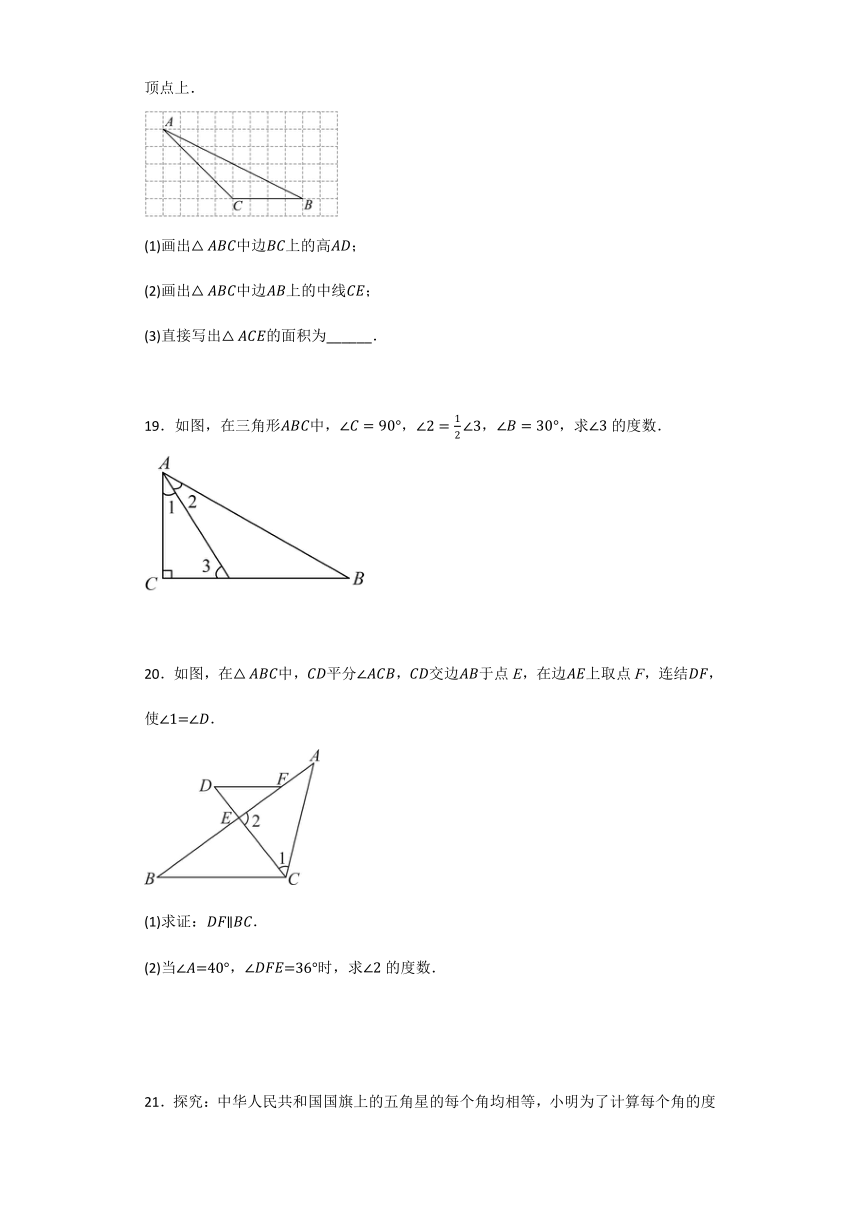
15.图形的密铺(或称图形的镶嵌)指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间既不留空隙、也不互相重叠地把一部分平面完全覆盖.图1所示的是一种五边形密铺的结构图,图2是从该密铺图案中抽象出的一个五边形,其中,,则的度数是________.
16.(1)如图①,____________ .
(2)如图②,____________.
(3)如图③,的度数为____________.
(4)一个不规则的图形如图④所示,那么____________.
三、解答题
17.已知在中,、、的对边分别为a、b、c.
(1)化简代数式:______.
(2)若,,求的各内角度数.
18.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出中边上的高;
(2)画出中边上的中线;
(3)直接写出的面积为______.
19.如图,在三角形中,,,,求的度数.
20.如图,在中,平分,交边于点E,在边上取点F,连结,使.
(1)求证:.
(2)当时,求的度数.
21.探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
(1)解:∵,.
∴ .
∵ ________,
∴________,
∴________.
(2)拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求,,,,的和.
(3)应用:如图③.小明将图②中的点落在上,点落在上,若,则________.
22.如图,四边形中,,平分,、交于点.
(1)如图1,若,
①求证:;
②作平分,如图2,求证:.
(2)如图3,作平分,在锐角内部作射线,交于N,若的大小为,试说明:平分
参考答案
1.解:A、3+4=7,不能构成三角形;
B、5+6>10,能构成三角形;
C、2+3<6,不能构成三角形;
D、5+6=11,不能构成三角形.
故选:B.
2.解:A.线段是的高,选项不符合题意;
B.线段是的高,选项不符合题意;
C.线段是的高,选项不符合题意;
D.线段是的高,选项符合题意.
故选:D.
3.解:A、B、C选项中都有四边形,只有C选项中只有三角形,根据四边形的不稳定性和三角形的稳定性可知:C选项的图形具有稳定性.
故选C.
4.解:∵,,四边形内角和为度,
∴,
故选:C.
5.C
6.解:,,
,
平分,
,
,
,
,
故选A.
7.解:A.正方形的每个内角是,正六边形的每个内角是,,取任何正整数时,不能得正整数,故不能铺满,A选项不符合题意;
B.正八边形的每个内角是,正六边形的每个内角是,,取任何正整数时,不能得正整数,故不能铺满,B选项不符合题意;
C.正十二形的每个内角是,正六边形的每个内角是,,取任何正整数时,不能得正整数,故不能铺满,C选项不符合题意;
D.正方形的每个内角是,正六边形的每个内角是,正十二形的每个内角是,,故能铺满,D选项符合题意.
故选:D.
8.解:是的中线,的面积为20,
,
是的中线,
,
故选:B.
9.解:设这个多边形边数为,
则,
解得:,
故答案为:7.
10.解:∵,,
∴,
∵是三角形的角平分线,
∴,
∵是三角形的高,
∴,
∴,
∴,
故答案为:.
11.解:如图,延长交于点F,
根据三角形外角的性质可得,
又 ,
,
,
,
,
故答案为:.
12.解:∵正五边形,
∴,
∵正方形,
∴,
∴,
∵,
∴.
故答案为:.
13.解:如图,
∵,
∴,
∴,
∴,
∴.
故答案为:230.
14.解:令相交于点M,相交于点P,
∵、的平分线交于,
∴,,
设,
∴,
,
得: ,
整理得:,
同理可得:,
,
,
故答案为:.
15.解:∵,,,
∴,则,
故答案为:.
16.解:如图①,连接,记,的交点为,
由三角形的内角和定理可得:
,
∵,
∴,
∴
;
如图②,连接,
同理可得:,
∴
;
如图③,
同理可得:,,,
∴
;
如图④,连接,
同理可得:,
∴
.
故答案为:,,,.
17.(1)解:∵a、b、c为三角形的三边,
∴,,
∴,,
∴
.
故答案为:.
(2)解:∵,,
∴,
∵,
∴,
解得:,
∴,,
综上:,,.
18.(1)解:如图,线段即为所求;
(2)如图,线段即为所求;
(3).
故答案为:4.
19.解:∵,,
∴,
设,则,,
∵,
∴,
解得:,
∴.
20.解:(1)∵是的平分线,
∴,
∵,
∴,
∴;
(2)∵,
∴,
∵,
∴
∵是的平分线,
∴,
∵
∴.
21.解:(1),.
.
,
,
;
(2),.
.
,
;
(3).
22.(1)证明:①∵,,
∴,
∵,
∴;
②∵平分,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴;
(2)证明:延长、交于点M,如图所示:
∵,
∴,
∴
,
∵平分,
∴,
∵平分,
∴,
∵,
∴,
∴
,
∴,
∴平分.
一、单选题
1.下列长度的三条线段,能组成三角形的是( )
A.3,4,7 B.5,6,10 C.2,3,6 D.5,6,11
2.下面四个图形中,线段是的高的图形是( )
A. B.
C. D.
3.下列图形中,具有稳定性的是( )
A. B. C. D.
4.一块四边形玻璃被打破,如图所示.小红想制做一模一样的玻璃,经测量,,则的度数( )
A. B. C. D.
5.一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A.12 B.13 C.14 D.15
6.如图,已知在中,是的角平分线,是边上的高,,,求的度数为( )
A. B. C. D.
7.正六边形和下列边长相同的正多边形地砖组合中,能铺满地面的是( )
A.正方形 B.正八边形
C.正十二边形 D.正四边形和正十二边形
8.如图已知是的中线,是的中线,若的面积为20,则的面积为( )
A.5 B.10 C.15 D.18
二、填空题
9.一个多边形的内角和与外角和的差为,则它的边数为______.
10.如图,在中,,,和分别是它的高和角平分线,则________.
11.如图,已知,若,则的度数为_____.
12.正五边形和正方形位置如图所示,连接,则的度数为______.
13.如图,四边形中,,若沿图中虚线剪去,则________.
14.如图,、的平分线交于,;、的平分线交于,;如此下去,、的平分线的交角为;…若,,则为________度.
15.图形的密铺(或称图形的镶嵌)指用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间既不留空隙、也不互相重叠地把一部分平面完全覆盖.图1所示的是一种五边形密铺的结构图,图2是从该密铺图案中抽象出的一个五边形,其中,,则的度数是________.
16.(1)如图①,____________ .
(2)如图②,____________.
(3)如图③,的度数为____________.
(4)一个不规则的图形如图④所示,那么____________.
三、解答题
17.已知在中,、、的对边分别为a、b、c.
(1)化简代数式:______.
(2)若,,求的各内角度数.
18.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出中边上的高;
(2)画出中边上的中线;
(3)直接写出的面积为______.
19.如图,在三角形中,,,,求的度数.
20.如图,在中,平分,交边于点E,在边上取点F,连结,使.
(1)求证:.
(2)当时,求的度数.
21.探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
(1)解:∵,.
∴ .
∵ ________,
∴________,
∴________.
(2)拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求,,,,的和.
(3)应用:如图③.小明将图②中的点落在上,点落在上,若,则________.
22.如图,四边形中,,平分,、交于点.
(1)如图1,若,
①求证:;
②作平分,如图2,求证:.
(2)如图3,作平分,在锐角内部作射线,交于N,若的大小为,试说明:平分
参考答案
1.解:A、3+4=7,不能构成三角形;
B、5+6>10,能构成三角形;
C、2+3<6,不能构成三角形;
D、5+6=11,不能构成三角形.
故选:B.
2.解:A.线段是的高,选项不符合题意;
B.线段是的高,选项不符合题意;
C.线段是的高,选项不符合题意;
D.线段是的高,选项符合题意.
故选:D.
3.解:A、B、C选项中都有四边形,只有C选项中只有三角形,根据四边形的不稳定性和三角形的稳定性可知:C选项的图形具有稳定性.
故选C.
4.解:∵,,四边形内角和为度,
∴,
故选:C.
5.C
6.解:,,
,
平分,
,
,
,
,
故选A.
7.解:A.正方形的每个内角是,正六边形的每个内角是,,取任何正整数时,不能得正整数,故不能铺满,A选项不符合题意;
B.正八边形的每个内角是,正六边形的每个内角是,,取任何正整数时,不能得正整数,故不能铺满,B选项不符合题意;
C.正十二形的每个内角是,正六边形的每个内角是,,取任何正整数时,不能得正整数,故不能铺满,C选项不符合题意;
D.正方形的每个内角是,正六边形的每个内角是,正十二形的每个内角是,,故能铺满,D选项符合题意.
故选:D.
8.解:是的中线,的面积为20,
,
是的中线,
,
故选:B.
9.解:设这个多边形边数为,
则,
解得:,
故答案为:7.
10.解:∵,,
∴,
∵是三角形的角平分线,
∴,
∵是三角形的高,
∴,
∴,
∴,
故答案为:.
11.解:如图,延长交于点F,
根据三角形外角的性质可得,
又 ,
,
,
,
,
故答案为:.
12.解:∵正五边形,
∴,
∵正方形,
∴,
∴,
∵,
∴.
故答案为:.
13.解:如图,
∵,
∴,
∴,
∴,
∴.
故答案为:230.
14.解:令相交于点M,相交于点P,
∵、的平分线交于,
∴,,
设,
∴,
,
得: ,
整理得:,
同理可得:,
,
,
故答案为:.
15.解:∵,,,
∴,则,
故答案为:.
16.解:如图①,连接,记,的交点为,
由三角形的内角和定理可得:
,
∵,
∴,
∴
;
如图②,连接,
同理可得:,
∴
;
如图③,
同理可得:,,,
∴
;
如图④,连接,
同理可得:,
∴
.
故答案为:,,,.
17.(1)解:∵a、b、c为三角形的三边,
∴,,
∴,,
∴
.
故答案为:.
(2)解:∵,,
∴,
∵,
∴,
解得:,
∴,,
综上:,,.
18.(1)解:如图,线段即为所求;
(2)如图,线段即为所求;
(3).
故答案为:4.
19.解:∵,,
∴,
设,则,,
∵,
∴,
解得:,
∴.
20.解:(1)∵是的平分线,
∴,
∵,
∴,
∴;
(2)∵,
∴,
∵,
∴
∵是的平分线,
∴,
∵
∴.
21.解:(1),.
.
,
,
;
(2),.
.
,
;
(3).
22.(1)证明:①∵,,
∴,
∵,
∴;
②∵平分,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴;
(2)证明:延长、交于点M,如图所示:
∵,
∴,
∴
,
∵平分,
∴,
∵平分,
∴,
∵,
∴,
∴
,
∴,
∴平分.
