南通 二面角的课件[下学期]
图片预览





文档简介
课件25张PPT。几何的简洁美正是几何学之所以完美的核心所在 —牛顿第一章 立体几何初步 CAI课件两平面位置关系—二面角
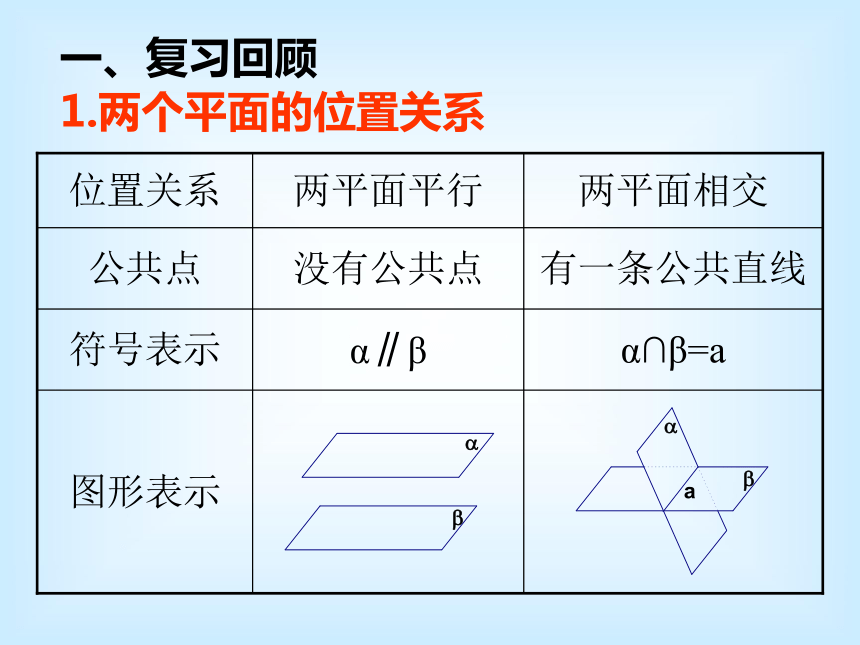
普通高中课程标准实验教科书(必修)数学2启东市汇龙中学高一数学 黄 靓一、复习回顾1.两个平面的位置关系2.在平面几何中“角”是怎样定义的?从一点出发的两条射线所组成的图形叫做角。或: 一条射线绕其端点旋转而成的图形叫做角。问题1.上面的是我们以前平面几何中角的形成,
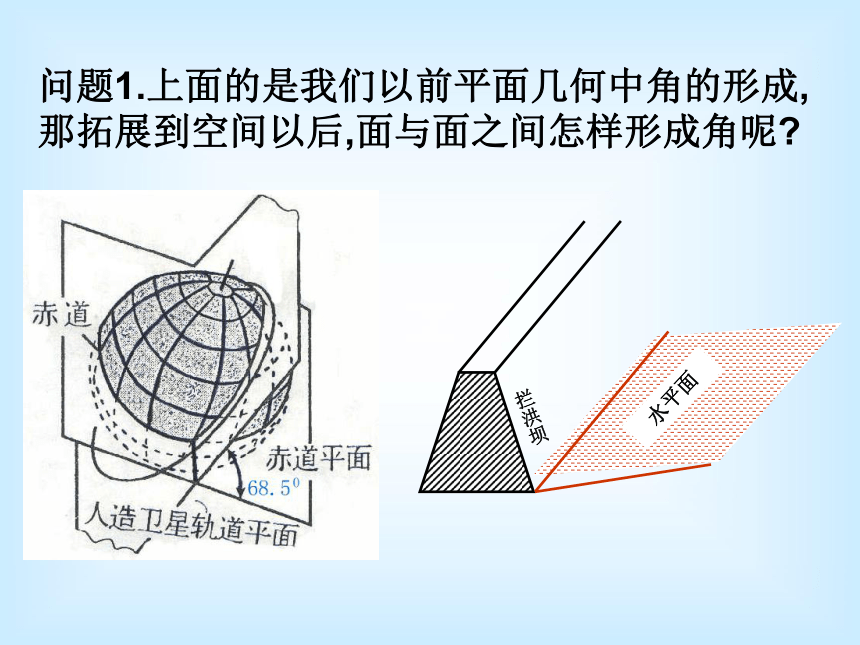
那拓展到空间以后,面与面之间怎样形成角呢?问题2.请同学们拿出一张纸,你能否用这张纸
制作这种数学模型吗?问题3.当我们把这张纸沿着其中的一条直线折
叠,就得到刻画空间两个相交平面的图形—
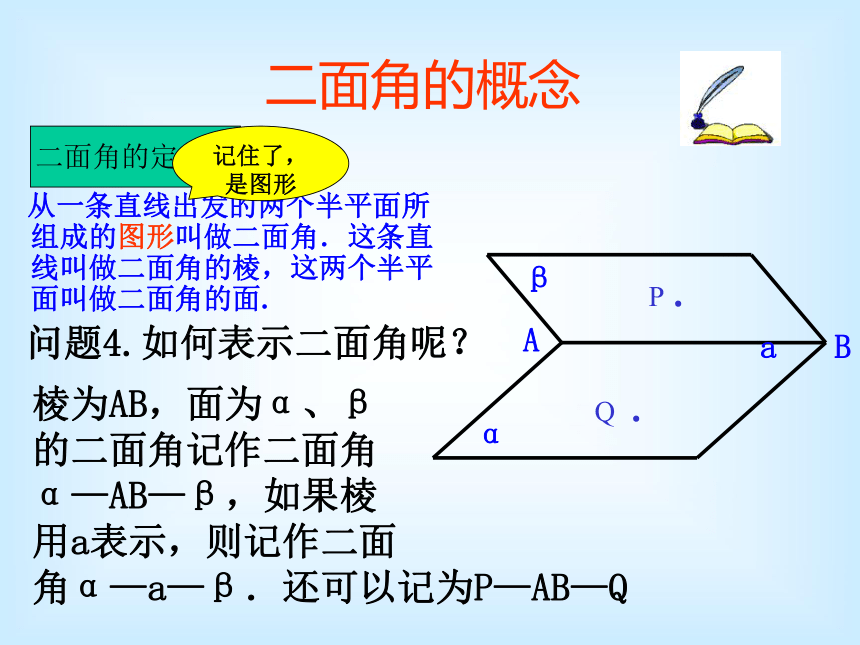
二面角,对于这种“角”如何定义呢?二面角的概念 从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面. 问题4.如何表示二面角呢?棱为AB,面为α、β
的二面角记作二面角
α—AB—β,如果棱
用a表示,则记作二面
角α—a—β.还可以记为P—AB—Q 二面角的定义:P .Q .记住了,是图形二面角的画法通常有两种:
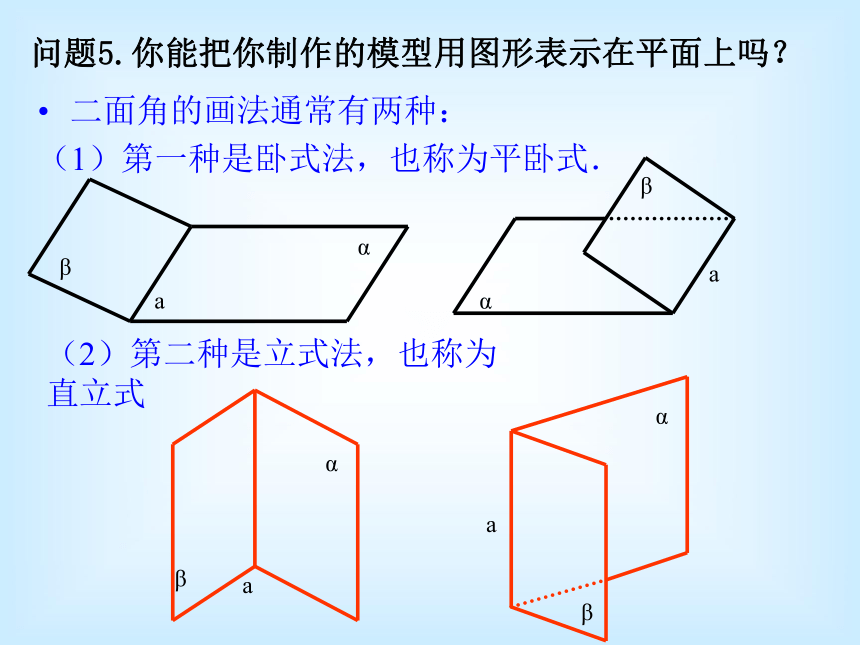
(1)第一种是卧式法,也称为平卧式.问题5.你能把你制作的模型用图形表示在平面上吗?(2)第二种是立式法,也称为直立式定义:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.问题6.当纸板沿着折痕不断打开的时候,我们
感到两个面构成的二面角在逐渐变大,如何来
刻画这个二面角的大小?二面角的平面角错误1错误2异面直线所成的角、直线和平面所成的角与有什么共同的特征?它们的共同特征都是将空间的角化归为两直线在同一平面内的的角。思考问题7.二面角的平面角必须满足哪几个条件?三个条件:
二、是平面角的两边分别在二面角的两个面内;三、是二面角的平面角的两条边都与棱垂直。
一、是平面角的顶点必在棱上;
问题8.二面角α-l-β的平面角∠AOB的大小
与点O的位置有关吗?答:无 关演示
特别规定:当二面角的两个面重合时,二面角的大小为0°,当二面角的两个面合成一个平面时,二面角的大小为180°。二面角的大小:1、二面角是指 ( )
A.两个平面相交所组成的图形
B.一个平面绕这个平面内一条直线旋转所组成
的图形
C.从一个平面内的一条直线出发的一个半平面
与这个平面所组成的图形
D.从一条直线出发的两个半平面所组成的图形D2、二面角的平面角指的是( )
A 分别在两个面内引棱的两条垂线所成的角
B 过棱上任意一点引棱的两条垂线所成的角
C过棱上任意一点,分别在两半平面面内引的两条射线
所成的角
D以棱上任意一点为端点,分别在两个面内作
与棱垂直的两条射线所成的角C练一练例1.如图,在正方体ABCD-A1B1C1D1中:
⑴求二面角D1-AB-D的大小;
⑵求二面角A1-AB-D的大小.解:(1)在正方体ABCD-A1B1C1D1中,AB⊥平面AD’,∴AB⊥ AD’,AB⊥AD∴∠D’AD即为二面角D1-AB-D的平面角在Rt△D’AD中,∠D’AD= ,所以二面角D1-AB-D的大小为(2)同理,∠A’AD为二面角A1-AB-D的平面角,二面角 A1-AB-D的大小为变式:如图,在正方体ABCD-A1B1C1D1中:
求二面角A1-BD-A的正切值。OD1若求二面角A1-BD-C的正切值呢?tan∠A1DC=课堂竞技场例2 已知在一个60°的二面角的棱上有两个点A、B,AC、BD分别是在这个二面角的两个面内,且垂直于AB的线段,又知AB=4cm,AC=6cm,BD=6cm,求CD的长。 ABCDE解:驶向胜利的彼岸在平面ABCD中,过D点、A点分别作DE∥AB,AE∥BD交于E点,则四边形ABDE是平行四边形,连接CE分析:首先构造这个二面角的平面角∵BD⊥AB ∴AE⊥AB 又AC⊥AB
∴∠CAE就是二面角的平面角,即∠CAE= 60° 在△ACE中,AE=BD=6,AC=6 ∴CE=6∵ AE⊥AB, AC⊥AB,AE∩AC=A ∴AB⊥平面ACE又DE∥AB ,∴DE⊥平面ACE ∴ DE⊥CEDE=AB=6练练:如图二面角α-l-β中,CA⊥l于A,BD⊥l于B,又知AB=4cm,AC=6cm,BD=6cm,CD= ,求二面角α-l-β的大小。E
数学实践二面角α-l-β的平面角是60°例3:如图,河堤斜面与水平面所成的二面角为60°,堤面上有一条直道CE,它与堤脚的水平线CF的夹角为30°,沿这条直道从堤脚上行走到10m时人升高了多少? 作业:如图,山坡的倾斜度(坡面与水平面所成二面角的度数)是60°,山坡上有一条直道CD,它和坡脚的水平线AB的夹角是30°,沿这条路上山,行走100米后升高多少米? 从上面练习中,我们可以总结几种作二面角的平面角的一般方法.
1.定义法:以二面角的棱上某一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角即二面角的平面角回顾反思2.作垂面法:作棱的垂面,则它和二面角的两个面的交线所成的角就是二面角的平面角课堂总结一、二面角的定义二、二面角的表示方法三、二面角的平面角四、二面角的平面角的作法五、二面角的计算
解题规律:
1、求二面角的步骤:
“作”-“证”-“说”- “求”- “答” 。
2、解决二面角的关键是作(找)平面角,通常有二种方法:①定义法;②作垂面法。
作业 :讲义后的课后研学汇龙中学校园一景再见!全国绿色学校汇龙中学欢迎您!
普通高中课程标准实验教科书(必修)数学2启东市汇龙中学高一数学 黄 靓一、复习回顾1.两个平面的位置关系2.在平面几何中“角”是怎样定义的?从一点出发的两条射线所组成的图形叫做角。或: 一条射线绕其端点旋转而成的图形叫做角。问题1.上面的是我们以前平面几何中角的形成,
那拓展到空间以后,面与面之间怎样形成角呢?问题2.请同学们拿出一张纸,你能否用这张纸
制作这种数学模型吗?问题3.当我们把这张纸沿着其中的一条直线折
叠,就得到刻画空间两个相交平面的图形—
二面角,对于这种“角”如何定义呢?二面角的概念 从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面. 问题4.如何表示二面角呢?棱为AB,面为α、β
的二面角记作二面角
α—AB—β,如果棱
用a表示,则记作二面
角α—a—β.还可以记为P—AB—Q 二面角的定义:P .Q .记住了,是图形二面角的画法通常有两种:
(1)第一种是卧式法,也称为平卧式.问题5.你能把你制作的模型用图形表示在平面上吗?(2)第二种是立式法,也称为直立式定义:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.问题6.当纸板沿着折痕不断打开的时候,我们
感到两个面构成的二面角在逐渐变大,如何来
刻画这个二面角的大小?二面角的平面角错误1错误2异面直线所成的角、直线和平面所成的角与有什么共同的特征?它们的共同特征都是将空间的角化归为两直线在同一平面内的的角。思考问题7.二面角的平面角必须满足哪几个条件?三个条件:
二、是平面角的两边分别在二面角的两个面内;三、是二面角的平面角的两条边都与棱垂直。
一、是平面角的顶点必在棱上;
问题8.二面角α-l-β的平面角∠AOB的大小
与点O的位置有关吗?答:无 关演示
特别规定:当二面角的两个面重合时,二面角的大小为0°,当二面角的两个面合成一个平面时,二面角的大小为180°。二面角的大小:1、二面角是指 ( )
A.两个平面相交所组成的图形
B.一个平面绕这个平面内一条直线旋转所组成
的图形
C.从一个平面内的一条直线出发的一个半平面
与这个平面所组成的图形
D.从一条直线出发的两个半平面所组成的图形D2、二面角的平面角指的是( )
A 分别在两个面内引棱的两条垂线所成的角
B 过棱上任意一点引棱的两条垂线所成的角
C过棱上任意一点,分别在两半平面面内引的两条射线
所成的角
D以棱上任意一点为端点,分别在两个面内作
与棱垂直的两条射线所成的角C练一练例1.如图,在正方体ABCD-A1B1C1D1中:
⑴求二面角D1-AB-D的大小;
⑵求二面角A1-AB-D的大小.解:(1)在正方体ABCD-A1B1C1D1中,AB⊥平面AD’,∴AB⊥ AD’,AB⊥AD∴∠D’AD即为二面角D1-AB-D的平面角在Rt△D’AD中,∠D’AD= ,所以二面角D1-AB-D的大小为(2)同理,∠A’AD为二面角A1-AB-D的平面角,二面角 A1-AB-D的大小为变式:如图,在正方体ABCD-A1B1C1D1中:
求二面角A1-BD-A的正切值。OD1若求二面角A1-BD-C的正切值呢?tan∠A1DC=课堂竞技场例2 已知在一个60°的二面角的棱上有两个点A、B,AC、BD分别是在这个二面角的两个面内,且垂直于AB的线段,又知AB=4cm,AC=6cm,BD=6cm,求CD的长。 ABCDE解:驶向胜利的彼岸在平面ABCD中,过D点、A点分别作DE∥AB,AE∥BD交于E点,则四边形ABDE是平行四边形,连接CE分析:首先构造这个二面角的平面角∵BD⊥AB ∴AE⊥AB 又AC⊥AB
∴∠CAE就是二面角的平面角,即∠CAE= 60° 在△ACE中,AE=BD=6,AC=6 ∴CE=6∵ AE⊥AB, AC⊥AB,AE∩AC=A ∴AB⊥平面ACE又DE∥AB ,∴DE⊥平面ACE ∴ DE⊥CEDE=AB=6练练:如图二面角α-l-β中,CA⊥l于A,BD⊥l于B,又知AB=4cm,AC=6cm,BD=6cm,CD= ,求二面角α-l-β的大小。E
数学实践二面角α-l-β的平面角是60°例3:如图,河堤斜面与水平面所成的二面角为60°,堤面上有一条直道CE,它与堤脚的水平线CF的夹角为30°,沿这条直道从堤脚上行走到10m时人升高了多少? 作业:如图,山坡的倾斜度(坡面与水平面所成二面角的度数)是60°,山坡上有一条直道CD,它和坡脚的水平线AB的夹角是30°,沿这条路上山,行走100米后升高多少米? 从上面练习中,我们可以总结几种作二面角的平面角的一般方法.
1.定义法:以二面角的棱上某一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角即二面角的平面角回顾反思2.作垂面法:作棱的垂面,则它和二面角的两个面的交线所成的角就是二面角的平面角课堂总结一、二面角的定义二、二面角的表示方法三、二面角的平面角四、二面角的平面角的作法五、二面角的计算
解题规律:
1、求二面角的步骤:
“作”-“证”-“说”- “求”- “答” 。
2、解决二面角的关键是作(找)平面角,通常有二种方法:①定义法;②作垂面法。
作业 :讲义后的课后研学汇龙中学校园一景再见!全国绿色学校汇龙中学欢迎您!
