2022-2023学年沪科版七年级数学下册《第10章相交线、平行线与平移》期末综合复习训练题(含答案)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学下册《第10章相交线、平行线与平移》期末综合复习训练题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 474.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 09:06:16 | ||
图片预览

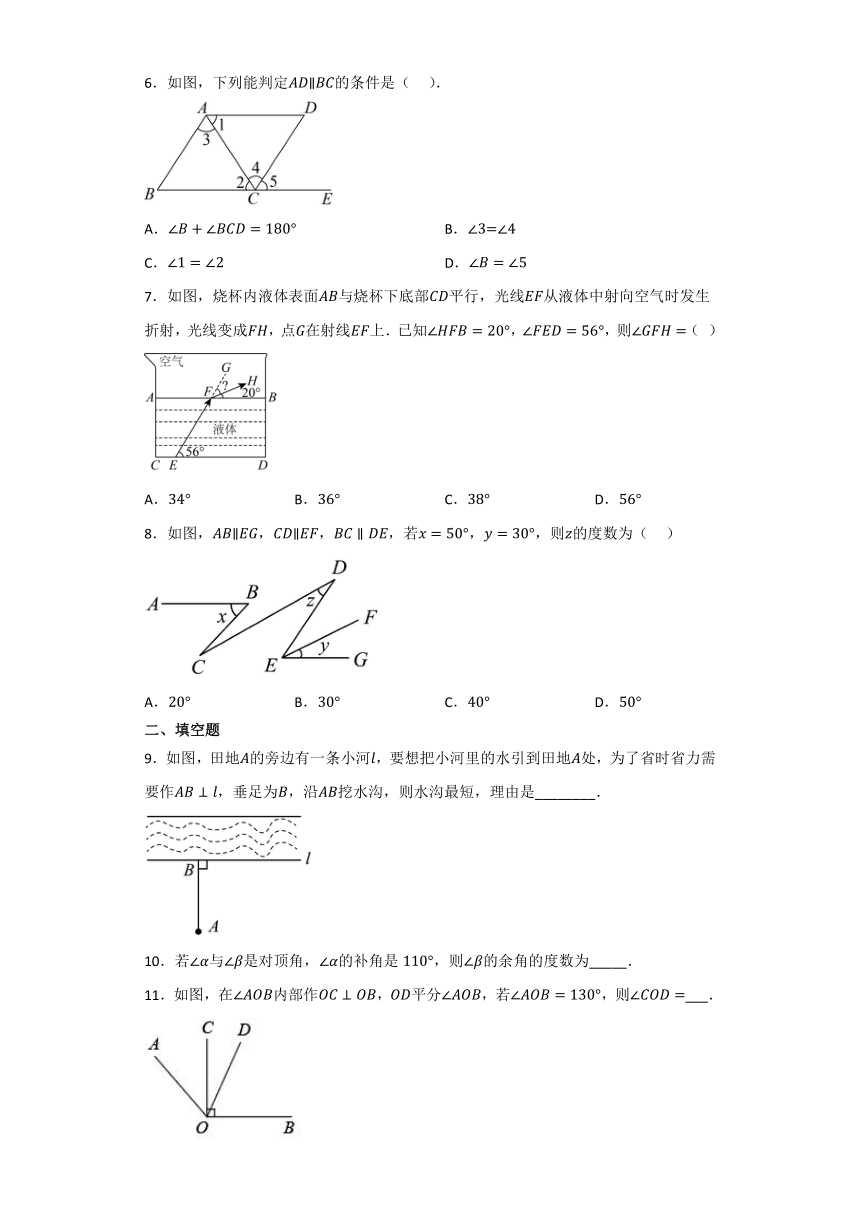
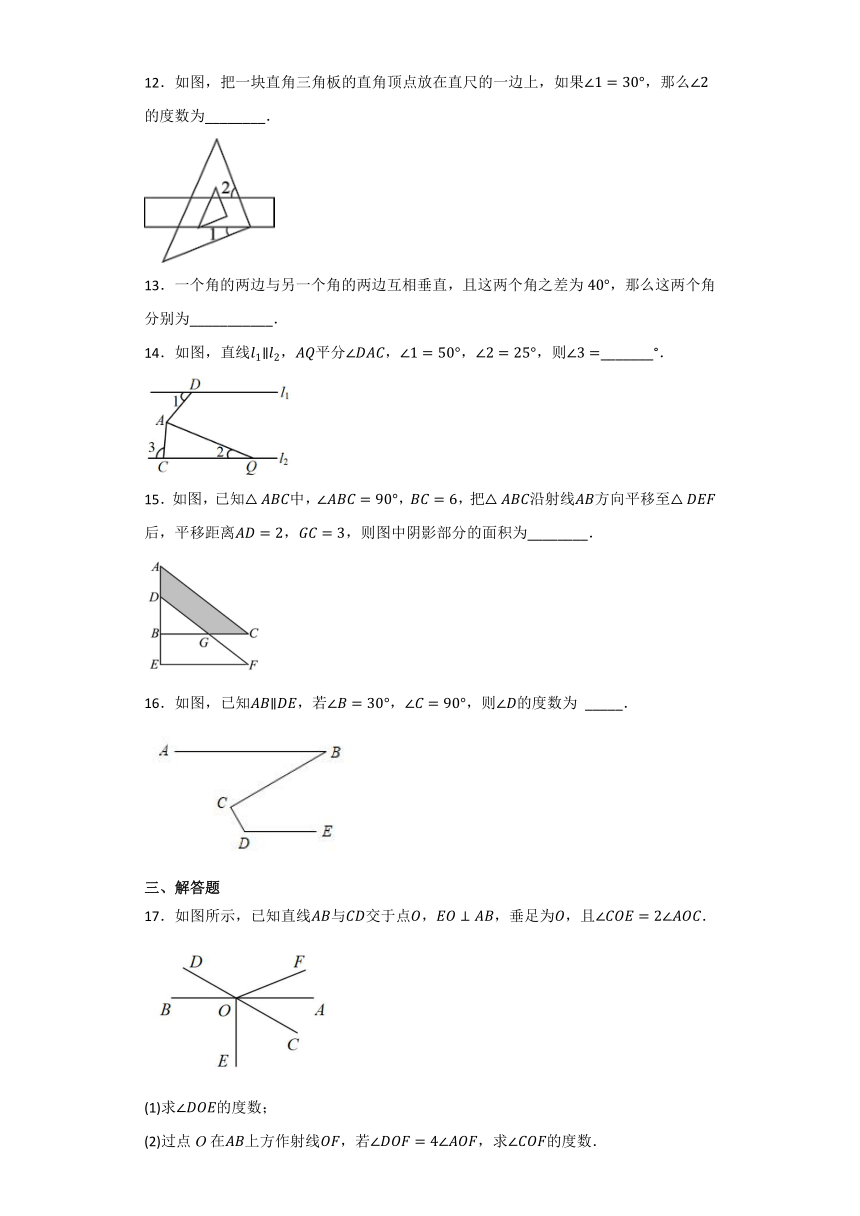


文档简介
2022-2023学年沪科版七年级数学下册《第10章相交线、平行线与平移》
期末综合复习训练题(附答案)
一、单选题
1.下列运动属于平移的是( )
A.转动的电风扇的叶片
B.打气筒打气时活塞的运动
C.行驶的自行车的后轮
D.在游乐场荡秋千的小朋友
2.下列说法中正确的有( )
①两条直线相交,所得的四个角中有一个角是,这两条直线一定互相垂直;
②两条直线的交点叫垂足;
③直线,也可以说成直线;
④两条直线不是平行就是互相垂直.
A.1个 B.2个 C.3个 D.4个
3.点P是直线l外一点,A,B,C为直线l上的三点,若,则点P到直线l的距离( )
A.小于 B.等于 C.不大于 D.大于
4.如图,直线被直线所截, ,,则的度数为( )
A. B. C. D.
5.如图,将木条,与钉在一起,,,要使木条与平行,木条旋转的度数至少是( )
A. B. C. D.
6.如图,下列能判定的条件是( ).
A. B.
C. D.
7.如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成,点在射线上.已知,,则( )
A. B. C. D.
8.如图,,,,若,,则的度数为( )
A. B. C. D.
二、填空题
9.如图,田地的旁边有一条小河,要想把小河里的水引到田地处,为了省时省力需要作,垂足为,沿挖水沟,则水沟最短,理由是________.
10.若与是对顶角,的补角是,则的余角的度数为_____.
11.如图,在内部作,平分,若,则___.
12.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果,那么的度数为________.
13.一个角的两边与另一个角的两边互相垂直,且这两个角之差为,那么这两个角分别为___________.
14.如图,直线,平分,,,则_______°.
15.如图,已知中,,,把沿射线方向平移至后,平移距离,,则图中阴影部分的面积为________.
16.如图,已知,若,则的度数为 _____.
三、解答题
17.如图所示,已知直线与交于点,,垂足为,且.
(1)求的度数;
(2)过点O在上方作射线,若,求的度数.
18.如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形的顶点都在正方形网格的格点上,将三角形向上平移m个单位,再向右平移n个单位,平移后得到三角形,其中图中直线l上的点是点A的对应点.
(1)画出平移后得到的三角形;
(2) ;
(3)在直线l上存在一点D,使所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
19.如图,.
试说明,根据图形,完成下列推理:
∵(已知)
∴(等量代换)
∴________//_________(_______________)
∵相交,
∴(____________)
∵
∴
∴ (___________________)
20.如图,已知,.
(1)试判断与的位置关系,并说明理由.
(2)若平分,,求的度数.
21.如图,,.
(1)如图1,直接写出与之间的数量关系________.
(2)如图2,写出与之间的数量关系,并说明理由.
(3)经过上述探究,可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________.
(4)已知与的两边分别平行,且比的倍小,求的度数.
22.(1)问题发现:如图①,直线,E是与之间的一点,连接,可以发现.请把下面的证明过程补充完整:
证明:过点E作,
∵(已知),(辅助线的作法),
∴,
∴_______.
∵,
∴_______,
∴_______.
即.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,求证:.
(3)解决问题:如图③,,,则是多少度?
参考答案
1.解:A、转动的电风扇的叶片,不属于平移,故A选项错误;
B、打气筒打气时活塞的运动沿直线运动,符合平移定义,属于平移,故B选项正确;
C、行驶的自行车的后轮是旋转,不属于平移,故C选项错误;
D、在游乐场荡秋千的小朋友,不属于平移,故D选项错误.
故选B.
2.解:根据对顶角和邻补角的性质,可得相交的四个角都为,所以两直线垂直,故①正确;
互相垂直的两条直线的交点叫垂足,故②错误;
直线,也可以说成直线,故③正确;
同一平面内,两条直线不是平行就是相交,不一定垂直,故④错误;
故选:B.
3.解:∵垂线段最短,
∴点P到直线l的距离为不大于.
故选:C.
4.解:
∵,,
∴.
∵,
∴.
故选A.
5.解:∵时,,
∴要使木条a与b平行,木条a旋转的度数至少是.
故选:C.
6.解:A、,,不能得到,本选项不符合题意;
B、,,不能得到,本选项符合题意.
C、,∴,本选项符合题意;
D、,,不能得到,本选项不符合题意;
故选:C.
7.解:∵,点在射线上,,
∴,
∵,,
∴,
故选:.
8.解:如图,延长交于点,
∵,
∴
∵,,
∴,,
∴,
即.
∴
故选:A
9.解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
10.解:∵的补角是,
∴,
∵与是对顶角,
∴,
∴的余角的度为,
故答案为:.
11.解:,平分,
,
,
,
,
故答案为:.
12.解:如图所示,由题意得,
∴,
故答案为:.
13.解:设较小的角为,则较大的角为,
依题意得:
解得:
则较大的角为:
故答案为:,.
14.解:过点作,
∴,
∵,
∴,
∴
∴,
∵平分,
∴,
∵,
∴,
故答案为:100.
15.解:∵沿射线方向平移至后,,平移距离为2,,,
∴,,
∵,
∴,
∵
∴,
∴,
故答案为:9.
16.解:如图:过点C作,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
故答案为:120°.
17.(1)解:∵,
∴,
∵,,
∴,
∴;
(2)∵,,
∴,
∵,
∴,
∴,
∴.
18.解:(1)如图所示:即为所求;
(2)根据题意可得,
∴
(3)∵,
∴四边形的面积是△ABC面积的2倍,
如图所示:画出符合题意的点D,一共 2个符合题意的D点.
19.解:∵(已知)
∴(等量代换)
∴ (同位角相等,两直线平行)
∵AB,DE相交,
∴(对顶角相等)
∵
∴
∴ (同旁内角互补,两直线平行)
故答案为:,,同位角相等,两直线平行;对顶角相等;,,同旁内角互补,两直线平行.
20.(1)解:.理由如下:
∵,,
∴,
∴,
∴,
又∵,
∴,
∴.
(2)解:∵平分,
∴,
又∵,
∴,
∵,
∴,
又∵,
∴,
解得,
∴,
又∵,
∴.
21.(1)解:如图,设与交于点.
,
,
,
,
,
故答案为: ;
(2)解:,
理由:如图:
,
,
,
,
;
故答案为:;
(3)综上所述,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;
故答案为:相等或互补;
(4)解:由题意,得,
分两种情况讨论:
①当时,,
解得,
,
②当时,,
解得,
,
综上所述,的度数是或.
22.(1)证明:如图①,
∵(已知),(辅助线的作法),
∴,
∴,
∵,
∴,
∴,
即,
故答案为:;
(2)证明:如图②,过点E作,
∵(已知),(辅助线的作法),
∴(平行于同一直线的两直线平行),
∴,
∴,
∴;
(3)解:如图③,过点E作,
∵(已知),(辅助线的作法),
∴(平行于同一直线的两直线平行),
∴,
∵,
∴,
∴,
∴∠A=∠AEF=20°.
故答案为:.
期末综合复习训练题(附答案)
一、单选题
1.下列运动属于平移的是( )
A.转动的电风扇的叶片
B.打气筒打气时活塞的运动
C.行驶的自行车的后轮
D.在游乐场荡秋千的小朋友
2.下列说法中正确的有( )
①两条直线相交,所得的四个角中有一个角是,这两条直线一定互相垂直;
②两条直线的交点叫垂足;
③直线,也可以说成直线;
④两条直线不是平行就是互相垂直.
A.1个 B.2个 C.3个 D.4个
3.点P是直线l外一点,A,B,C为直线l上的三点,若,则点P到直线l的距离( )
A.小于 B.等于 C.不大于 D.大于
4.如图,直线被直线所截, ,,则的度数为( )
A. B. C. D.
5.如图,将木条,与钉在一起,,,要使木条与平行,木条旋转的度数至少是( )
A. B. C. D.
6.如图,下列能判定的条件是( ).
A. B.
C. D.
7.如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成,点在射线上.已知,,则( )
A. B. C. D.
8.如图,,,,若,,则的度数为( )
A. B. C. D.
二、填空题
9.如图,田地的旁边有一条小河,要想把小河里的水引到田地处,为了省时省力需要作,垂足为,沿挖水沟,则水沟最短,理由是________.
10.若与是对顶角,的补角是,则的余角的度数为_____.
11.如图,在内部作,平分,若,则___.
12.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果,那么的度数为________.
13.一个角的两边与另一个角的两边互相垂直,且这两个角之差为,那么这两个角分别为___________.
14.如图,直线,平分,,,则_______°.
15.如图,已知中,,,把沿射线方向平移至后,平移距离,,则图中阴影部分的面积为________.
16.如图,已知,若,则的度数为 _____.
三、解答题
17.如图所示,已知直线与交于点,,垂足为,且.
(1)求的度数;
(2)过点O在上方作射线,若,求的度数.
18.如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形的顶点都在正方形网格的格点上,将三角形向上平移m个单位,再向右平移n个单位,平移后得到三角形,其中图中直线l上的点是点A的对应点.
(1)画出平移后得到的三角形;
(2) ;
(3)在直线l上存在一点D,使所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
19.如图,.
试说明,根据图形,完成下列推理:
∵(已知)
∴(等量代换)
∴________//_________(_______________)
∵相交,
∴(____________)
∵
∴
∴ (___________________)
20.如图,已知,.
(1)试判断与的位置关系,并说明理由.
(2)若平分,,求的度数.
21.如图,,.
(1)如图1,直接写出与之间的数量关系________.
(2)如图2,写出与之间的数量关系,并说明理由.
(3)经过上述探究,可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________.
(4)已知与的两边分别平行,且比的倍小,求的度数.
22.(1)问题发现:如图①,直线,E是与之间的一点,连接,可以发现.请把下面的证明过程补充完整:
证明:过点E作,
∵(已知),(辅助线的作法),
∴,
∴_______.
∵,
∴_______,
∴_______.
即.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,求证:.
(3)解决问题:如图③,,,则是多少度?
参考答案
1.解:A、转动的电风扇的叶片,不属于平移,故A选项错误;
B、打气筒打气时活塞的运动沿直线运动,符合平移定义,属于平移,故B选项正确;
C、行驶的自行车的后轮是旋转,不属于平移,故C选项错误;
D、在游乐场荡秋千的小朋友,不属于平移,故D选项错误.
故选B.
2.解:根据对顶角和邻补角的性质,可得相交的四个角都为,所以两直线垂直,故①正确;
互相垂直的两条直线的交点叫垂足,故②错误;
直线,也可以说成直线,故③正确;
同一平面内,两条直线不是平行就是相交,不一定垂直,故④错误;
故选:B.
3.解:∵垂线段最短,
∴点P到直线l的距离为不大于.
故选:C.
4.解:
∵,,
∴.
∵,
∴.
故选A.
5.解:∵时,,
∴要使木条a与b平行,木条a旋转的度数至少是.
故选:C.
6.解:A、,,不能得到,本选项不符合题意;
B、,,不能得到,本选项符合题意.
C、,∴,本选项符合题意;
D、,,不能得到,本选项不符合题意;
故选:C.
7.解:∵,点在射线上,,
∴,
∵,,
∴,
故选:.
8.解:如图,延长交于点,
∵,
∴
∵,,
∴,,
∴,
即.
∴
故选:A
9.解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
10.解:∵的补角是,
∴,
∵与是对顶角,
∴,
∴的余角的度为,
故答案为:.
11.解:,平分,
,
,
,
,
故答案为:.
12.解:如图所示,由题意得,
∴,
故答案为:.
13.解:设较小的角为,则较大的角为,
依题意得:
解得:
则较大的角为:
故答案为:,.
14.解:过点作,
∴,
∵,
∴,
∴
∴,
∵平分,
∴,
∵,
∴,
故答案为:100.
15.解:∵沿射线方向平移至后,,平移距离为2,,,
∴,,
∵,
∴,
∵
∴,
∴,
故答案为:9.
16.解:如图:过点C作,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
故答案为:120°.
17.(1)解:∵,
∴,
∵,,
∴,
∴;
(2)∵,,
∴,
∵,
∴,
∴,
∴.
18.解:(1)如图所示:即为所求;
(2)根据题意可得,
∴
(3)∵,
∴四边形的面积是△ABC面积的2倍,
如图所示:画出符合题意的点D,一共 2个符合题意的D点.
19.解:∵(已知)
∴(等量代换)
∴ (同位角相等,两直线平行)
∵AB,DE相交,
∴(对顶角相等)
∵
∴
∴ (同旁内角互补,两直线平行)
故答案为:,,同位角相等,两直线平行;对顶角相等;,,同旁内角互补,两直线平行.
20.(1)解:.理由如下:
∵,,
∴,
∴,
∴,
又∵,
∴,
∴.
(2)解:∵平分,
∴,
又∵,
∴,
∵,
∴,
又∵,
∴,
解得,
∴,
又∵,
∴.
21.(1)解:如图,设与交于点.
,
,
,
,
,
故答案为: ;
(2)解:,
理由:如图:
,
,
,
,
;
故答案为:;
(3)综上所述,如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补;
故答案为:相等或互补;
(4)解:由题意,得,
分两种情况讨论:
①当时,,
解得,
,
②当时,,
解得,
,
综上所述,的度数是或.
22.(1)证明:如图①,
∵(已知),(辅助线的作法),
∴,
∴,
∵,
∴,
∴,
即,
故答案为:;
(2)证明:如图②,过点E作,
∵(已知),(辅助线的作法),
∴(平行于同一直线的两直线平行),
∴,
∴,
∴;
(3)解:如图③,过点E作,
∵(已知),(辅助线的作法),
∴(平行于同一直线的两直线平行),
∴,
∵,
∴,
∴,
∴∠A=∠AEF=20°.
故答案为:.
同课章节目录
