广东省佛山市南海区2022-2023学年九年级下学期6月月考数学试题(含答案)
文档属性
| 名称 | 广东省佛山市南海区2022-2023学年九年级下学期6月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 09:20:45 | ||
图片预览



文档简介
2022-2023学年平洲初三下学期6月大测数学试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.在,,,中,无理数为( )
A. B. C. D.
2.下列图形中,是中心对称图形的是( )
A. B. C. D.
3.下列运算中,正确的是( )
A. B. C. D.
4.甲、乙两人在相同条件下,各射击10次,经计算:甲射击成绩的平均数是9环,方差是1.4;乙射击成绩的平均数是9环,方差是0.8.下列说法中一定正确的是( )
A.甲的总环数大于乙的总环数 B.甲的成绩比乙的成绩稳定
C.甲、乙成绩的众数相同 D.乙的成绩比甲的成绩波动小
5.点(3,)在正比例函数的图象上,则k的值为( )
A. B. C. D.
6.如图,,,,则( )
A.62° B.118° C.31° D.59°
7.一元二次方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
8.已知反比例函数经过点(1,4),下列说法正确的是( )
A.这个函数的图象位于第二、四象限
B.当时,y随x的增大而减小
C.当时,y随x的增大而增大
D.该反比例函数图像会经过点
9.如图,长方形纸片ABCD中,已知,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且,则AB的长为( )
A.3 B.4 C.5 D.6
10.如图,在Rt中,,,动点D从点A出发,沿线段AB以1单位长度/秒的速度运动,当点D与点B重合时,运动停止.以AD为一边向上作正方形ADEF,若设运动时间为x秒(),正方形ADEF与重合部分的面积为y,则下列能大致反映y与x的函数关系的图象是( )
B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解: .
12.将抛物线向右平移1个单位,再向上平移3个单位后,得到的抛物线解析式是 .
13.如图,平行四边形ABCD中,已知cm,cm,DE平分交BC边于点E,则
cm.
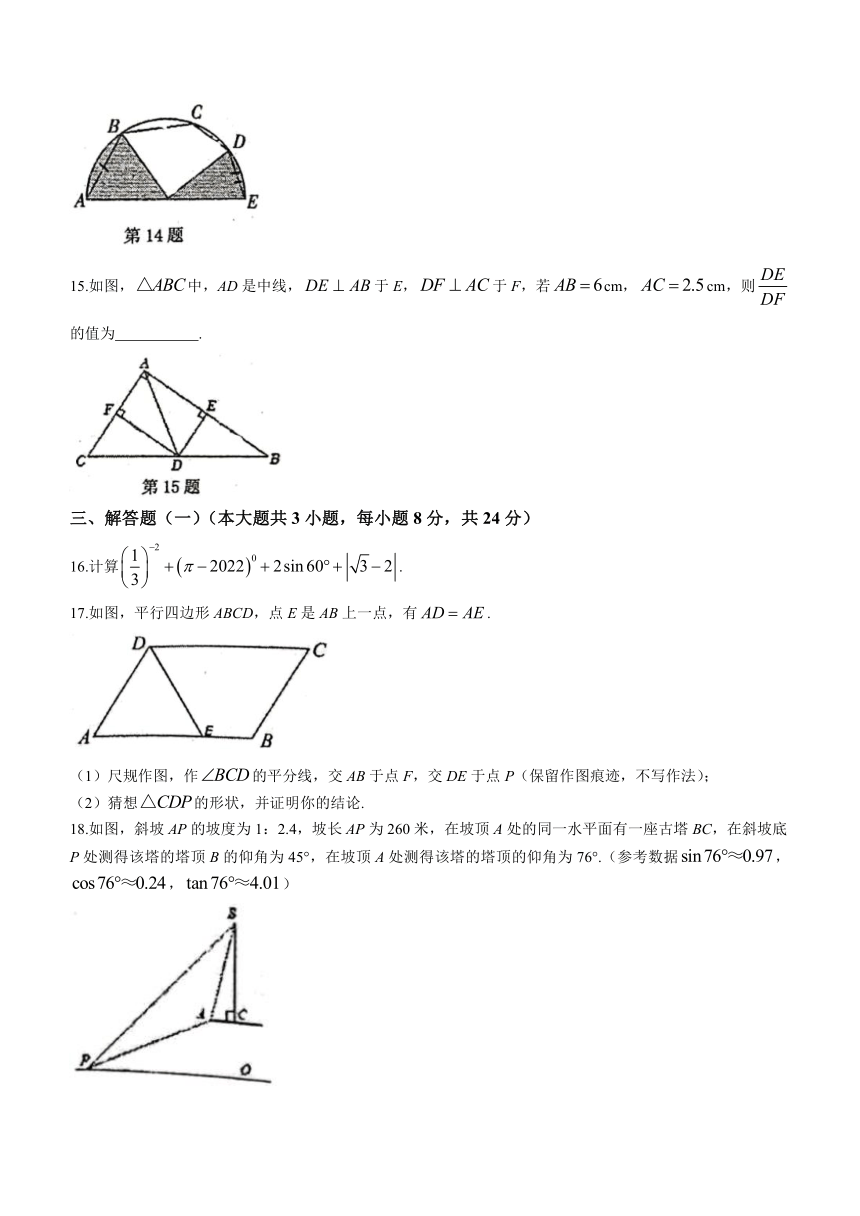
14.如图,半圆O的直径,点B,C,D均在半圆上,若,,连接OB,OD,则图中阴影部分的面积为 .
15.如图,中,AD是中线,于E,于F,若cm,cm,则的值为 .
三、解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算.
17.如图,平行四边形ABCD,点E是AB上一点,有.
(1)尺规作图,作的平分线,交AB于点F,交DE于点P(保留作图痕迹,不写作法);
(2)猜想的形状,并证明你的结论.
18.如图,斜坡AP的坡度为1:2.4,坡长AP为260米,在坡顶A处的同一水平面有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶的仰角为76°.(参考数据,,)
(1)求坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
四、解答题(二)(本大题共3小题,每小题9分,共27分)
19.生态优先,绿色发展,让美丽的地球添上更多“中国绿”,某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的1.5倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.
(1)求甲、乙两种树苗单价分别是多少元?
(2)为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?
20.中国共产党的助手和后备军——中国共青团,担负着为中国特色社会主义事业培养合格建设者和可靠接班人的根本任务,成立一百周年之际,各中学持续开展了A:青年大学习;B:青年学党史;C:中国梦宣传教育:D:社会主义核心价值观培育践行等一系列活动,学生可以任选一项参加,为了解学生参与情况,进行了一次抽样调查,根据收集的数据绘制了两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生1180名,请估计参加B项活动的学生数;
(3)小王和小林参加了上述活动,请用列表或画树状图的方法,求他们参加同一项活动的概率.
21.如图,在四边形ABCD中,,,对角线AC,BD交于点O,AC平,过点C作交AB的延长线于点E,连接.
(1)求证:BD垂直平分AC;
(2)若,,求OE的长.
五、解答题(三)(本大题共2小题,每小题12分,共24分)
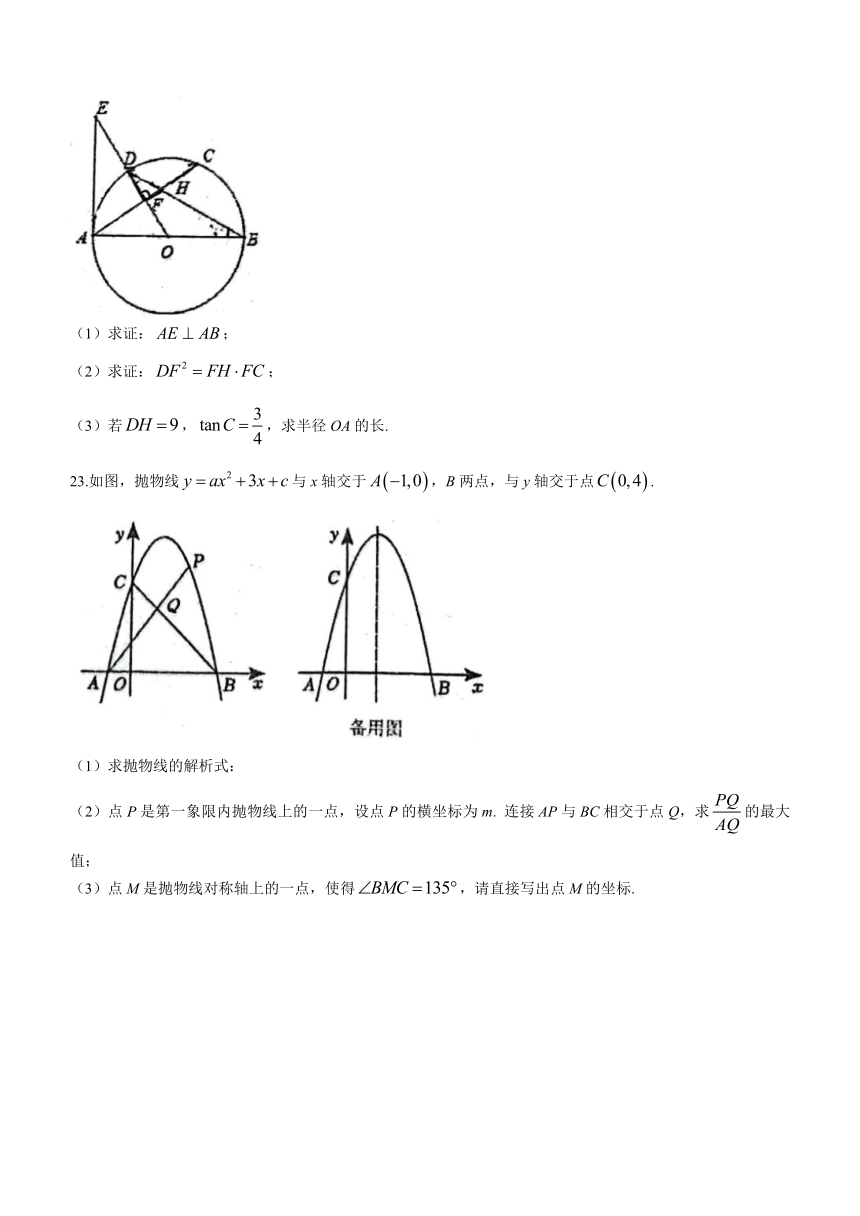
22.如图,AB是的直径,C是上一点,F是弦AC的中点,E为OD延长线上一点,且,AC与BD交于点H,与OE交于点F.
(1)求证:;
(2)求证:;
(3)若,,求半径OA的长.
23.如图,抛物线与x轴交于,B两点,与y轴交于点.
(1)求抛物线的解析式:
(2)点P是第一象限内抛物线上的一点,设点P的横坐标为m. 连接AP与BC相交于点Q,求的最大值;
(3)点M是抛物线对称轴上的一点,使得,请直接写出点M的坐标.
数学答案
1-5 DDDDD 6-10 ABBDB
11.
12.
13.6
14.
15.
16.解:原式……………………4
………………5(有1分,如果学生在第一步就将其化简为,则第一步5分)
………………8(没有上述所有过程,直接一步到位等于12的只给1分)
17.(1)解:
射线CF即为所求…………………………2
(2)解:是直角三角形,理由如下:………………………………3
四边形ABCD是平行四边形,
,
,
,即……………………4
平分,
………………………………5
,
…………………………6
,
………………………………7
是直角三角形…………………………8
18.解:(1)过点A作,有
斜坡AP的坡度为1∶2.4,即
设米,米(如果题目有单位,设的时候记得写单位)
由勾股定理,……………………………………………………1
解得
米……………………………………………………2
坡顶A到地面PO的距离为100米.……………………………………………3(所有实际应用的问题记得写答)
(2)延长BC交PO于点D
依题意,,,,m,,
,
…………………………4
设米,则,
米,
在Rt中,,
则,
即
解
解得…………………………7(如果学生列的是分式方程,没检验,不扣分)
答:古塔BC的高度为187米…………………………8(所有实际应用的问题记得写答)
19.(1)解:设乙种树苗单价的为x元,
根据题意有………………………………1
解得:…………………………………………………………2
经检验是原方程的解………………………………3
…………………………4
答:甲种树苗单价的为15元,则乙种树苗单价的为10元……………………5
(2)解:设购买乙种树苗m棵(如果题目有单位,设的时候记得写单位)
依题意:…………………………6
解得:…………………………7
m是正整数
m的最小整数解为38……………………8
答:乙种树苗至少购买38棵.……………………9
20.(1)在这次调查中,一共抽取了学生
(名),
(名),补全条形统计图如下:…………………………1
…………………………2
(3)(名),故估计参加B项活动的学生为472名;………………4
(4)画树状图如下:
…………………………7(不要用树状图,请用表格)
共有16种等 可能的结果,其中小王和小林参加同一项活动的结果有4种,
小王和小林参加同一项活动的概率为.…………………………9
21.(1)证明:,
,
平分,
,
,
……………………1
,
……………………2
四边形ABCD是平行四边形
四边形ABCD是菱形
BD垂直平分AC………………4(如果是用此方法,但没有先说明是菱形,直接下结论BD垂直平分AC,不给分)
此外,本题可能有学生用全等或其他方式证BD垂直平分AC,言之有理即可,请酌情给分
(1)解:设,则,
由(1)知四边形ABCD是菱形,
,
由勾股定理得…………………………6
解得或(舍去)…………………………7(没有将写出来的,摇号 一分)
………………………………8(用其他方法的,言之有理即可,请酌情给分)
,点O为AC的中点,
……………………9(没写“,点O为AC的中点”不给分)
22.解:(1)
是AC的中点,OD为半径
…………………………1
弧弧
,
……………………2
……………………3
…………………………4
(2),
弧弧
……………………6
,
………………7(部分同学没将摆出来,扣一分)
……………………8
(3)由(1)知
,
,
是的直径
…………………………10
由(2)知,即
设,,得
由勾股定理,
…………………………12
23.
解:(1)由题意得,
解得:,
则抛物线的表达式为:;……………………3(没有过程扣一分)
(2)令,解得,
则点……………………4
过点A、P分别作y轴的平行线交BC于点N、H,
由点B、C的坐标得,直线BC的表达式为:…………5
当时,,即点,则,
设点,则点
则……………………6
轴,
则,
故的最大值为;…………………………8
(3)或………………12(每个坐标2分)
法一 利用隐圆
法二 利用三角形相似
一、选择题(本大题共10小题,每小题3分,共30分)
1.在,,,中,无理数为( )
A. B. C. D.
2.下列图形中,是中心对称图形的是( )
A. B. C. D.
3.下列运算中,正确的是( )
A. B. C. D.
4.甲、乙两人在相同条件下,各射击10次,经计算:甲射击成绩的平均数是9环,方差是1.4;乙射击成绩的平均数是9环,方差是0.8.下列说法中一定正确的是( )
A.甲的总环数大于乙的总环数 B.甲的成绩比乙的成绩稳定
C.甲、乙成绩的众数相同 D.乙的成绩比甲的成绩波动小
5.点(3,)在正比例函数的图象上,则k的值为( )
A. B. C. D.
6.如图,,,,则( )
A.62° B.118° C.31° D.59°
7.一元二次方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
8.已知反比例函数经过点(1,4),下列说法正确的是( )
A.这个函数的图象位于第二、四象限
B.当时,y随x的增大而减小
C.当时,y随x的增大而增大
D.该反比例函数图像会经过点
9.如图,长方形纸片ABCD中,已知,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且,则AB的长为( )
A.3 B.4 C.5 D.6
10.如图,在Rt中,,,动点D从点A出发,沿线段AB以1单位长度/秒的速度运动,当点D与点B重合时,运动停止.以AD为一边向上作正方形ADEF,若设运动时间为x秒(),正方形ADEF与重合部分的面积为y,则下列能大致反映y与x的函数关系的图象是( )
B. C. D.
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解: .
12.将抛物线向右平移1个单位,再向上平移3个单位后,得到的抛物线解析式是 .
13.如图,平行四边形ABCD中,已知cm,cm,DE平分交BC边于点E,则
cm.
14.如图,半圆O的直径,点B,C,D均在半圆上,若,,连接OB,OD,则图中阴影部分的面积为 .
15.如图,中,AD是中线,于E,于F,若cm,cm,则的值为 .
三、解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算.
17.如图,平行四边形ABCD,点E是AB上一点,有.
(1)尺规作图,作的平分线,交AB于点F,交DE于点P(保留作图痕迹,不写作法);
(2)猜想的形状,并证明你的结论.
18.如图,斜坡AP的坡度为1:2.4,坡长AP为260米,在坡顶A处的同一水平面有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶的仰角为76°.(参考数据,,)
(1)求坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
四、解答题(二)(本大题共3小题,每小题9分,共27分)
19.生态优先,绿色发展,让美丽的地球添上更多“中国绿”,某小区为抓好“园区绿化”,购买了甲、乙两种树苗,购买甲种树苗花了1200元,购买乙种树苗花了900元,甲种树苗的单价是乙种树苗的1.5倍,购买甲种树苗的数量比购买乙种树苗的数量少10棵.
(1)求甲、乙两种树苗单价分别是多少元?
(2)为扩大园区绿化面积,该小区准备再次购进甲、乙两种树苗共100棵,若总金额不超过1314元,问最少购进多少棵乙种树苗?
20.中国共产党的助手和后备军——中国共青团,担负着为中国特色社会主义事业培养合格建设者和可靠接班人的根本任务,成立一百周年之际,各中学持续开展了A:青年大学习;B:青年学党史;C:中国梦宣传教育:D:社会主义核心价值观培育践行等一系列活动,学生可以任选一项参加,为了解学生参与情况,进行了一次抽样调查,根据收集的数据绘制了两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生1180名,请估计参加B项活动的学生数;
(3)小王和小林参加了上述活动,请用列表或画树状图的方法,求他们参加同一项活动的概率.
21.如图,在四边形ABCD中,,,对角线AC,BD交于点O,AC平,过点C作交AB的延长线于点E,连接.
(1)求证:BD垂直平分AC;
(2)若,,求OE的长.
五、解答题(三)(本大题共2小题,每小题12分,共24分)
22.如图,AB是的直径,C是上一点,F是弦AC的中点,E为OD延长线上一点,且,AC与BD交于点H,与OE交于点F.
(1)求证:;
(2)求证:;
(3)若,,求半径OA的长.
23.如图,抛物线与x轴交于,B两点,与y轴交于点.
(1)求抛物线的解析式:
(2)点P是第一象限内抛物线上的一点,设点P的横坐标为m. 连接AP与BC相交于点Q,求的最大值;
(3)点M是抛物线对称轴上的一点,使得,请直接写出点M的坐标.
数学答案
1-5 DDDDD 6-10 ABBDB
11.
12.
13.6
14.
15.
16.解:原式……………………4
………………5(有1分,如果学生在第一步就将其化简为,则第一步5分)
………………8(没有上述所有过程,直接一步到位等于12的只给1分)
17.(1)解:
射线CF即为所求…………………………2
(2)解:是直角三角形,理由如下:………………………………3
四边形ABCD是平行四边形,
,
,
,即……………………4
平分,
………………………………5
,
…………………………6
,
………………………………7
是直角三角形…………………………8
18.解:(1)过点A作,有
斜坡AP的坡度为1∶2.4,即
设米,米(如果题目有单位,设的时候记得写单位)
由勾股定理,……………………………………………………1
解得
米……………………………………………………2
坡顶A到地面PO的距离为100米.……………………………………………3(所有实际应用的问题记得写答)
(2)延长BC交PO于点D
依题意,,,,m,,
,
…………………………4
设米,则,
米,
在Rt中,,
则,
即
解
解得…………………………7(如果学生列的是分式方程,没检验,不扣分)
答:古塔BC的高度为187米…………………………8(所有实际应用的问题记得写答)
19.(1)解:设乙种树苗单价的为x元,
根据题意有………………………………1
解得:…………………………………………………………2
经检验是原方程的解………………………………3
…………………………4
答:甲种树苗单价的为15元,则乙种树苗单价的为10元……………………5
(2)解:设购买乙种树苗m棵(如果题目有单位,设的时候记得写单位)
依题意:…………………………6
解得:…………………………7
m是正整数
m的最小整数解为38……………………8
答:乙种树苗至少购买38棵.……………………9
20.(1)在这次调查中,一共抽取了学生
(名),
(名),补全条形统计图如下:…………………………1
…………………………2
(3)(名),故估计参加B项活动的学生为472名;………………4
(4)画树状图如下:
…………………………7(不要用树状图,请用表格)
共有16种等 可能的结果,其中小王和小林参加同一项活动的结果有4种,
小王和小林参加同一项活动的概率为.…………………………9
21.(1)证明:,
,
平分,
,
,
……………………1
,
……………………2
四边形ABCD是平行四边形
四边形ABCD是菱形
BD垂直平分AC………………4(如果是用此方法,但没有先说明是菱形,直接下结论BD垂直平分AC,不给分)
此外,本题可能有学生用全等或其他方式证BD垂直平分AC,言之有理即可,请酌情给分
(1)解:设,则,
由(1)知四边形ABCD是菱形,
,
由勾股定理得…………………………6
解得或(舍去)…………………………7(没有将写出来的,摇号 一分)
………………………………8(用其他方法的,言之有理即可,请酌情给分)
,点O为AC的中点,
……………………9(没写“,点O为AC的中点”不给分)
22.解:(1)
是AC的中点,OD为半径
…………………………1
弧弧
,
……………………2
……………………3
…………………………4
(2),
弧弧
……………………6
,
………………7(部分同学没将摆出来,扣一分)
……………………8
(3)由(1)知
,
,
是的直径
…………………………10
由(2)知,即
设,,得
由勾股定理,
…………………………12
23.
解:(1)由题意得,
解得:,
则抛物线的表达式为:;……………………3(没有过程扣一分)
(2)令,解得,
则点……………………4
过点A、P分别作y轴的平行线交BC于点N、H,
由点B、C的坐标得,直线BC的表达式为:…………5
当时,,即点,则,
设点,则点
则……………………6
轴,
则,
故的最大值为;…………………………8
(3)或………………12(每个坐标2分)
法一 利用隐圆
法二 利用三角形相似
同课章节目录
