华师大版数学七年级上册 4.6 第3课时 余角和补角 课件(共15张PPT)
文档属性
| 名称 | 华师大版数学七年级上册 4.6 第3课时 余角和补角 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 237.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 10:53:10 | ||
图片预览





文档简介
(共15张PPT)
4.6 角
第3课时 余角和补角
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
想一想
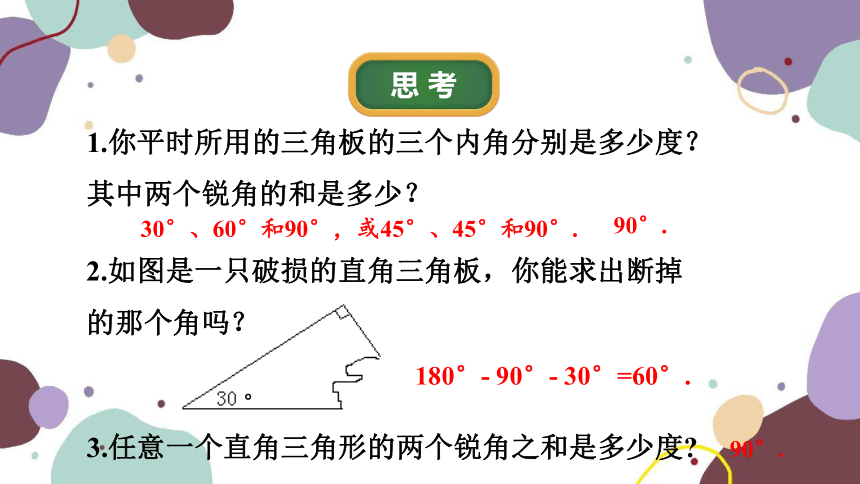
1.你平时所用的三角板的三个内角分别是多少度?其中两个锐角的和是多少?
2.如图是一只破损的直角三角板,你能求出断掉的那个角吗?
3.任意一个直角三角形的两个锐角之和是多少度
°
30°、60°和90°,或45°、45°和90°.
90°.
180°- 90°- 30°=60°.
90°.
思 考
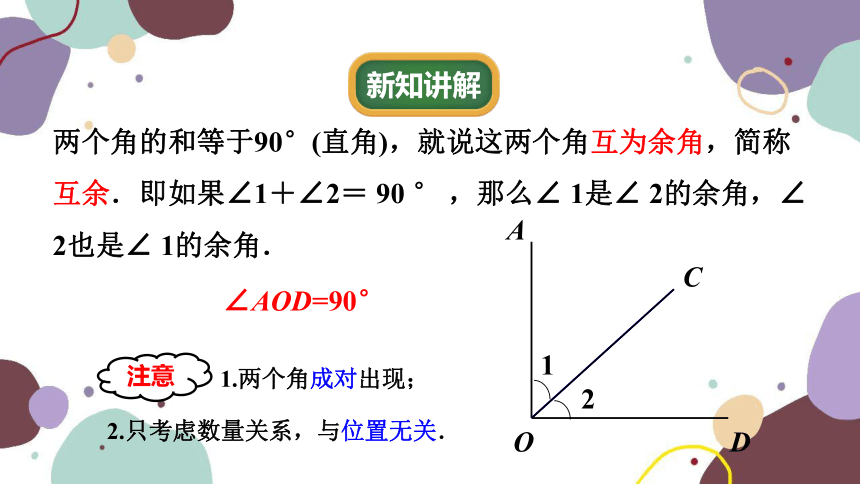
两个角的和等于90°(直角),就说这两个角互为余角,简称互余.即如果∠1+∠2= 90 ° ,那么∠ 1是∠ 2的余角,∠ 2也是∠ 1的余角.
O
A
D
C
1
2
2.只考虑数量关系,与位置无关.
∠AOD=90°
1.两个角成对出现;
注意
新知讲解
同角的余角相等.
1.任意画一个锐角,然后利用三角板中的直角画出这个角的余角.
结论
探 究
1
2
3
4
解:∠2=60°,
∠4=60°.
∠2=∠4.
2.如图, ∠1与∠2互余, ∠3与∠4互余,如果∠1=30°,∠3=30°,那么∠ 2与∠4分别等于多少度?∠2与∠4有什么关系?
2.如图, ∠1与∠2互余, ∠3与∠4互余,如果∠1=30°,∠3=30°,那么∠ 2与∠4分别等于多少度?∠2与∠4有什么关系?
等角的余角相等.
结论
如果两个角的和等于180°(平角) ,就说这两个角互为补角,简称互补.
(1)两个角成对出现;
(2)只考虑数量关系,与位置无关.
注意
同角(等角)的补角相等.
结论
新知讲解
1.填空:
某个角
它的余角
它的补角
34°
49°
50°30′
105°
x°
56°
41°
39°30′
(90-x)°
(180-x)°
146°
131°
129°30′
75°
例 题
2.若∠1=60°,则∠2,∠3,∠4分别是多少度
1
2
3
4
解:∠2=180°-∠1=180°-60°=120°,
∠3=180°-∠2=180°-120°=60°,
∠4=180°-∠1=180°-60°=120°.
例 题
3.已知∠α=50°17′,求∠α的余角和补角.
解: ∠α的余角=90°- 50°17′=39°43′,
∠α的余角和补角=180°-50°17′=129°43′.
例 题
1.判断:
(1)一个角的余角一定是锐角.( )
(2)一个角的补角一定是钝角.( )
(3)若∠1+ ∠2+ ∠3=90°,则∠1,∠2,∠3互为余角.( )
(4)28°30′的角的余角是62°30′.( )
(5)任何一个角都有余角.( )
√
×
×
×
×
练 习
O
A
B
C
2. 要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
解:延长AO至C,
∠AOB=180°-∠BOC,
所以只需测量出∠BOC的度数即可.
3. 如图,OD,OE分别是∠AOC, ∠BOC的角平分线.
(1)若∠AOC=110 °,则∠ BOC=______,∠ AOD=_______,
∠ COE=______,∠ AOE=______, ∠ DOE=______;
O
A
D
C
E
B
70°
55°
35°
145°
90°
(2)若∠ AOD=x°,你能用含x的代数式表示这个图形中的其他角吗
解:∠DOC=x°,∠BOE=∠COE=(90-x) °,
∠AOC=2x°,∠AOE=(90+x)°,
∠DOB=(180-x)°,∠COB=(180-2x)°.
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
性 质
数量关系
对应图形
互为补角
互为余角
总 结
4.6 角
第3课时 余角和补角
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
想一想
1.你平时所用的三角板的三个内角分别是多少度?其中两个锐角的和是多少?
2.如图是一只破损的直角三角板,你能求出断掉的那个角吗?
3.任意一个直角三角形的两个锐角之和是多少度
°
30°、60°和90°,或45°、45°和90°.
90°.
180°- 90°- 30°=60°.
90°.
思 考
两个角的和等于90°(直角),就说这两个角互为余角,简称互余.即如果∠1+∠2= 90 ° ,那么∠ 1是∠ 2的余角,∠ 2也是∠ 1的余角.
O
A
D
C
1
2
2.只考虑数量关系,与位置无关.
∠AOD=90°
1.两个角成对出现;
注意
新知讲解
同角的余角相等.
1.任意画一个锐角,然后利用三角板中的直角画出这个角的余角.
结论
探 究
1
2
3
4
解:∠2=60°,
∠4=60°.
∠2=∠4.
2.如图, ∠1与∠2互余, ∠3与∠4互余,如果∠1=30°,∠3=30°,那么∠ 2与∠4分别等于多少度?∠2与∠4有什么关系?
2.如图, ∠1与∠2互余, ∠3与∠4互余,如果∠1=30°,∠3=30°,那么∠ 2与∠4分别等于多少度?∠2与∠4有什么关系?
等角的余角相等.
结论
如果两个角的和等于180°(平角) ,就说这两个角互为补角,简称互补.
(1)两个角成对出现;
(2)只考虑数量关系,与位置无关.
注意
同角(等角)的补角相等.
结论
新知讲解
1.填空:
某个角
它的余角
它的补角
34°
49°
50°30′
105°
x°
56°
41°
39°30′
(90-x)°
(180-x)°
146°
131°
129°30′
75°
例 题
2.若∠1=60°,则∠2,∠3,∠4分别是多少度
1
2
3
4
解:∠2=180°-∠1=180°-60°=120°,
∠3=180°-∠2=180°-120°=60°,
∠4=180°-∠1=180°-60°=120°.
例 题
3.已知∠α=50°17′,求∠α的余角和补角.
解: ∠α的余角=90°- 50°17′=39°43′,
∠α的余角和补角=180°-50°17′=129°43′.
例 题
1.判断:
(1)一个角的余角一定是锐角.( )
(2)一个角的补角一定是钝角.( )
(3)若∠1+ ∠2+ ∠3=90°,则∠1,∠2,∠3互为余角.( )
(4)28°30′的角的余角是62°30′.( )
(5)任何一个角都有余角.( )
√
×
×
×
×
练 习
O
A
B
C
2. 要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
解:延长AO至C,
∠AOB=180°-∠BOC,
所以只需测量出∠BOC的度数即可.
3. 如图,OD,OE分别是∠AOC, ∠BOC的角平分线.
(1)若∠AOC=110 °,则∠ BOC=______,∠ AOD=_______,
∠ COE=______,∠ AOE=______, ∠ DOE=______;
O
A
D
C
E
B
70°
55°
35°
145°
90°
(2)若∠ AOD=x°,你能用含x的代数式表示这个图形中的其他角吗
解:∠DOC=x°,∠BOE=∠COE=(90-x) °,
∠AOC=2x°,∠AOE=(90+x)°,
∠DOB=(180-x)°,∠COB=(180-2x)°.
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等
同角或等角的补角相等
性 质
数量关系
对应图形
互为补角
互为余角
总 结
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
