2023年中考数学复习 考前冲刺(十三)课件(共25张PPT)
文档属性
| 名称 | 2023年中考数学复习 考前冲刺(十三)课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 11:45:54 | ||
图片预览





文档简介
(共25张PPT)
考前冲刺
考前冲刺(十三)
一、选择题(本大题10小题,每小题3分,共30分)
1.在实数5, , , 中无理数是( )
A.5 B. C. D.
2.如图,在数轴上,点A,B分别表示a,b,且a+b=0,若AB=6,
则点A表示的数为( )
A.-3 B.0 C.3 D.-6
C
A
3.2022年北京冬季奥运会的吉祥物冰墩墩(BingDwenDwen),因其造型
酷萌大受欢迎,截至2月18日又投入新春版冰墩墩18万个,市场上仍然
是“一墩难求”.将数据“18万”用科学记数法表示为( )
A.18×104 B.1.8×105
C.1.8×106 D.0.18×107
B
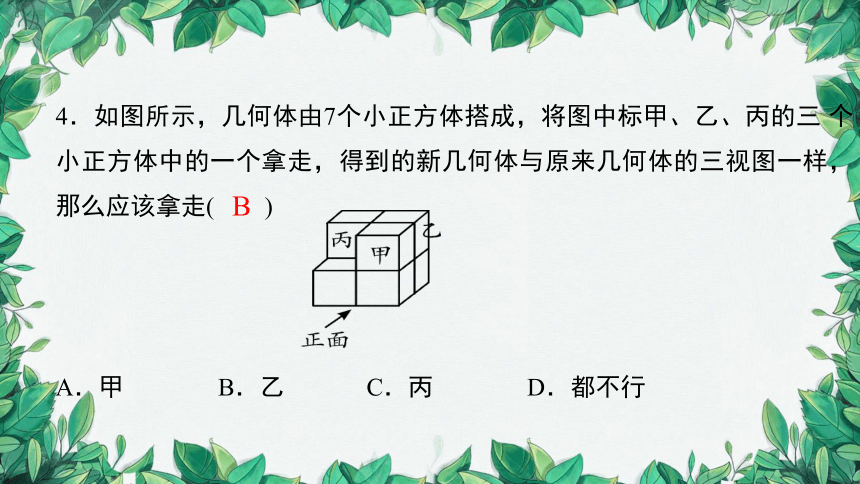
4.如图所示,几何体由7个小正方体搭成,将图中标甲、乙、丙的三 个小正方体中的一个拿走,得到的新几何体与原来几何体的三视图一样,那么应该拿走( )
A.甲 B.乙 C.丙 D.都不行
B
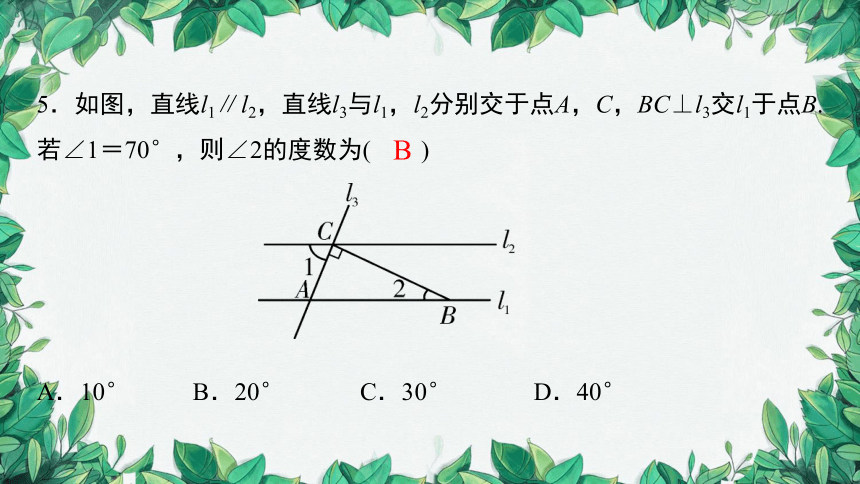
5.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B.若∠1=70°,则∠2的度数为( )
A.10° B.20° C.30° D.40°
B
6.在“践行生态文明,你我一起行动”主题有奖竞赛活动中,9年级(3)班共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是( )
A. B. C. D.
B
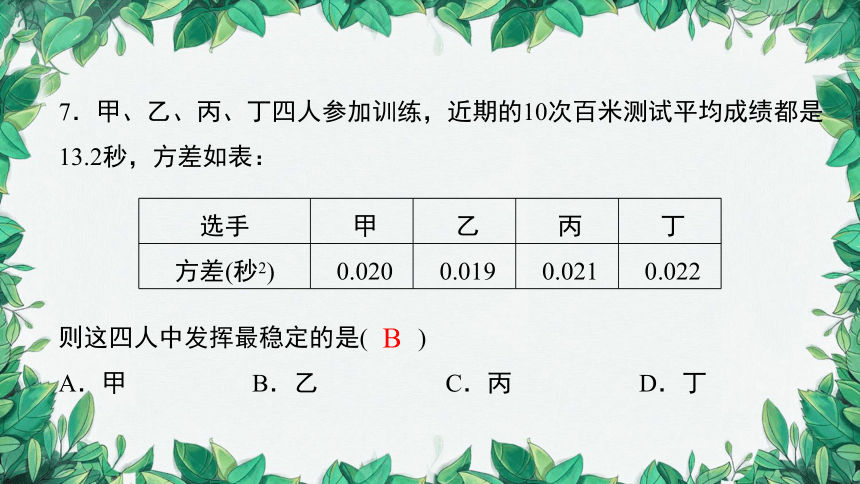
选手 甲 乙 丙 丁
方差(秒2) 0.020 0.019 0.021 0.022
7.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表:
则这四人中发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
B
8.端午节是我国首个入选世界非物质文化遗产的传统节日,吃粽子是端午节的习俗之一.某超市豆沙粽的进价比肉粽的进价每盒便宜10元,用6 000元购进豆沙粽的盒数和用8 000元购进肉粽的盒数相同.设豆沙粽每盒的进价为x元,可列方程为( )
B
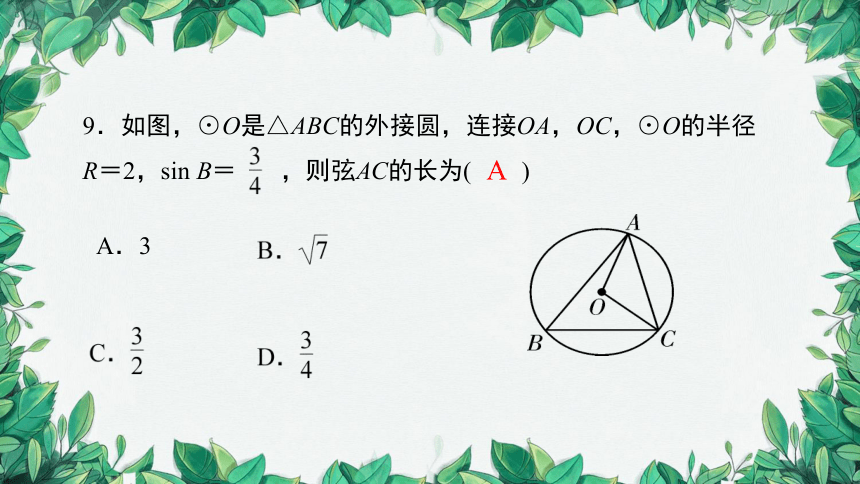
9.如图,⊙O是△ABC的外接圆,连接OA,OC,⊙O的半径R=2,sin B= ,则弦AC的长为( )
A.3
A
10.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )
A. B. C. D.
A
二、填空题(本大题5小题,每小题3分,共15分)
11.一元一次不等式组 的解集为__________.
12.若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为____________.
x≤1
x=-2
13.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-3,6),B(1,3),则方程ax2-bx-c=0的解是____________________.
x1=-3,x2=1
14.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点.若∠CAE=90°,AB=1,则BD=__________.
15.如图所示,菱形OEFG中,∠GOE=60°,GF=4,
点E在y = (k≠0)的图象上,则k=__________________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
解:原式=2-1+9=1+9=10
17.解不等式组: ,并把解在数轴上表示出来.
解:解不等式①得:x>2
解不等式②得:x<4
∴原不等式组的解集为:2<x<4
在数轴上表示如图所示:
18.如图,已知△ABC,∠C=90°,AC(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
解:(1)如图所示:点D即为所求;
(2)连结AD,若∠B=37°,求∠CAD的度数.
解:(2)在Rt△ABC中,∠B=37°,
∴∠CAB=53°,
又∵AD=BD,∴∠BAD=∠B=37°,
∴∠CAD=53°-37°=16°.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.如图,一次函数y1=-x-1的图象与x轴交于点A,
与y轴交于点B,与反比例函数y2= 的图象的一个交
点为M(-2,m),另一个交点为N.
(1)求反比例函数的解析式;
(2)求点B到直线OM的距离;
(3)在x轴上是否存在点P,使得△PMN为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
20.2022北京冬奥会期间,冰墩墩和雪容融受到人们的广泛喜爱.某网店以每套96元的价格购进了一批冰墩墩和雪容融,由于销售火爆,销售单价经过两次的调整,从每套150元上涨到每套216元,此时每天可售出16套冰墩墩和雪容融.
(1)若销售价格每次上涨的百分率相同,求每次上涨的百分率;
解:(1)设每次上涨的百分率为x,根据题意得:150(1+x)2=216,
解得:x1=0.2,x2=-2.2(不合题意,舍去),
答:每次上涨的百分率为20%;
(2)预计冬奥会闭幕后需求会有所下降,需尽快将这批冰墩墩和雪容触售出,该网店决定降价出售.经过市场调查发现:销售单价每降价10元,每天多卖出2
套.当降价钱数m为多少元时每天的利润W(元)可达到最大,最大利润是多少?
21.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,∴BC=EF,∴AD=EF,
∵AD∥EF,∴四边形AEFD是平行四边形,
∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
考前冲刺
考前冲刺(十三)
一、选择题(本大题10小题,每小题3分,共30分)
1.在实数5, , , 中无理数是( )
A.5 B. C. D.
2.如图,在数轴上,点A,B分别表示a,b,且a+b=0,若AB=6,
则点A表示的数为( )
A.-3 B.0 C.3 D.-6
C
A
3.2022年北京冬季奥运会的吉祥物冰墩墩(BingDwenDwen),因其造型
酷萌大受欢迎,截至2月18日又投入新春版冰墩墩18万个,市场上仍然
是“一墩难求”.将数据“18万”用科学记数法表示为( )
A.18×104 B.1.8×105
C.1.8×106 D.0.18×107
B
4.如图所示,几何体由7个小正方体搭成,将图中标甲、乙、丙的三 个小正方体中的一个拿走,得到的新几何体与原来几何体的三视图一样,那么应该拿走( )
A.甲 B.乙 C.丙 D.都不行
B
5.如图,直线l1∥l2,直线l3与l1,l2分别交于点A,C,BC⊥l3交l1于点B.若∠1=70°,则∠2的度数为( )
A.10° B.20° C.30° D.40°
B
6.在“践行生态文明,你我一起行动”主题有奖竞赛活动中,9年级(3)班共设置“生态知识、生态技能、生态习惯、生态文化”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是( )
A. B. C. D.
B
选手 甲 乙 丙 丁
方差(秒2) 0.020 0.019 0.021 0.022
7.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表:
则这四人中发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
B
8.端午节是我国首个入选世界非物质文化遗产的传统节日,吃粽子是端午节的习俗之一.某超市豆沙粽的进价比肉粽的进价每盒便宜10元,用6 000元购进豆沙粽的盒数和用8 000元购进肉粽的盒数相同.设豆沙粽每盒的进价为x元,可列方程为( )
B
9.如图,⊙O是△ABC的外接圆,连接OA,OC,⊙O的半径R=2,sin B= ,则弦AC的长为( )
A.3
A
10.如图,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是( )
A. B. C. D.
A
二、填空题(本大题5小题,每小题3分,共15分)
11.一元一次不等式组 的解集为__________.
12.若关于x的方程x2+3x+a=0有一个根为-1,则另一个根为____________.
x≤1
x=-2
13.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-3,6),B(1,3),则方程ax2-bx-c=0的解是____________________.
x1=-3,x2=1
14.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点.若∠CAE=90°,AB=1,则BD=__________.
15.如图所示,菱形OEFG中,∠GOE=60°,GF=4,
点E在y = (k≠0)的图象上,则k=__________________.
三、解答题(一)(本大题3小题,每小题8分,共24分)
解:原式=2-1+9=1+9=10
17.解不等式组: ,并把解在数轴上表示出来.
解:解不等式①得:x>2
解不等式②得:x<4
∴原不等式组的解集为:2<x<4
在数轴上表示如图所示:
18.如图,已知△ABC,∠C=90°,AC
解:(1)如图所示:点D即为所求;
(2)连结AD,若∠B=37°,求∠CAD的度数.
解:(2)在Rt△ABC中,∠B=37°,
∴∠CAB=53°,
又∵AD=BD,∴∠BAD=∠B=37°,
∴∠CAD=53°-37°=16°.
四、解答题(二)(本大题3小题,每小题9分,共27分)
19.如图,一次函数y1=-x-1的图象与x轴交于点A,
与y轴交于点B,与反比例函数y2= 的图象的一个交
点为M(-2,m),另一个交点为N.
(1)求反比例函数的解析式;
(2)求点B到直线OM的距离;
(3)在x轴上是否存在点P,使得△PMN为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
20.2022北京冬奥会期间,冰墩墩和雪容融受到人们的广泛喜爱.某网店以每套96元的价格购进了一批冰墩墩和雪容融,由于销售火爆,销售单价经过两次的调整,从每套150元上涨到每套216元,此时每天可售出16套冰墩墩和雪容融.
(1)若销售价格每次上涨的百分率相同,求每次上涨的百分率;
解:(1)设每次上涨的百分率为x,根据题意得:150(1+x)2=216,
解得:x1=0.2,x2=-2.2(不合题意,舍去),
答:每次上涨的百分率为20%;
(2)预计冬奥会闭幕后需求会有所下降,需尽快将这批冰墩墩和雪容触售出,该网店决定降价出售.经过市场调查发现:销售单价每降价10元,每天多卖出2
套.当降价钱数m为多少元时每天的利润W(元)可达到最大,最大利润是多少?
21.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,∴BC=EF,∴AD=EF,
∵AD∥EF,∴四边形AEFD是平行四边形,
∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
同课章节目录
