2023年广东省深圳市中考数学备考冲刺模拟卷(无答案)
文档属性
| 名称 | 2023年广东省深圳市中考数学备考冲刺模拟卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 723.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-20 20:42:12 | ||
图片预览


文档简介
2023年中考数学备考冲刺模拟卷
班级: 姓名:
一、选择题(共10小题,每小题3分,计30分)
1.下列互为倒数是( )
A.和 B.和-2 C.和-2 D.和
2.下面四个化学仪器示意图中,是轴对称图形的是( )
A. B. C. D.
3.深圳是改革开放后党和人民一手缔造的崭新城市,是中国特色社会主义在一张白纸上的精彩演绎。深圳广大干部群众披荆斩棘、埋头苦干,用40年的时间走过了国外一些国际大都市上百年走完的历程。深圳经济特区生机勃勃,向世界展示了我国改革开放的磅礴伟力,2022年深圳市年度GDP为32387万亿,用科学计数法表示2022年深圳GDP为( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C.( D.
5. 已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20°
B.30°
C.40°
D.50°
6.假如控制双眼皮的基因为A,控制单眼皮的基因为,(即基因为时,则为单眼皮)如图为一对夫妻的基因遗传图谱,则生一个孩子为双眼皮的概率为( )
A. B. C. D.
7. 下列命题错误的是( )
A.对角线相等的平行四边形是矩形 B.切线垂直于经过切点的半径
C.将一次函数图像向上平移1个单位得到的图像
有一组角相等及两边对应成比例的两个三角形相似
8.如图,在菱形ABCD中,AC=,∠ADC=120°,以点A
为圆心画圆弧交AC于点E,则阴影部分的面积为( )
A. B. C. D.
9. 我国古代数学名著九章算术中记载“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出钱,多出钱;每人出钱,还差钱.问人数、物价各是多少?若设共有人,物价是钱,则下列方程正确的是( )
A. B.
C. D.
10.如图,在矩形ABCD中,E为边AB上一点,将△ADE沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点G.若BF·AD=12,则AF的长度为( )
A.6 B.12
C. D.2
二、填空题(共5小题,每小题3分,计15分.)
11. 因式分解:=
12.如图,二次函数与x 轴交点坐标为(-1,0)(2,0)当y<0时,x 的取值范围是
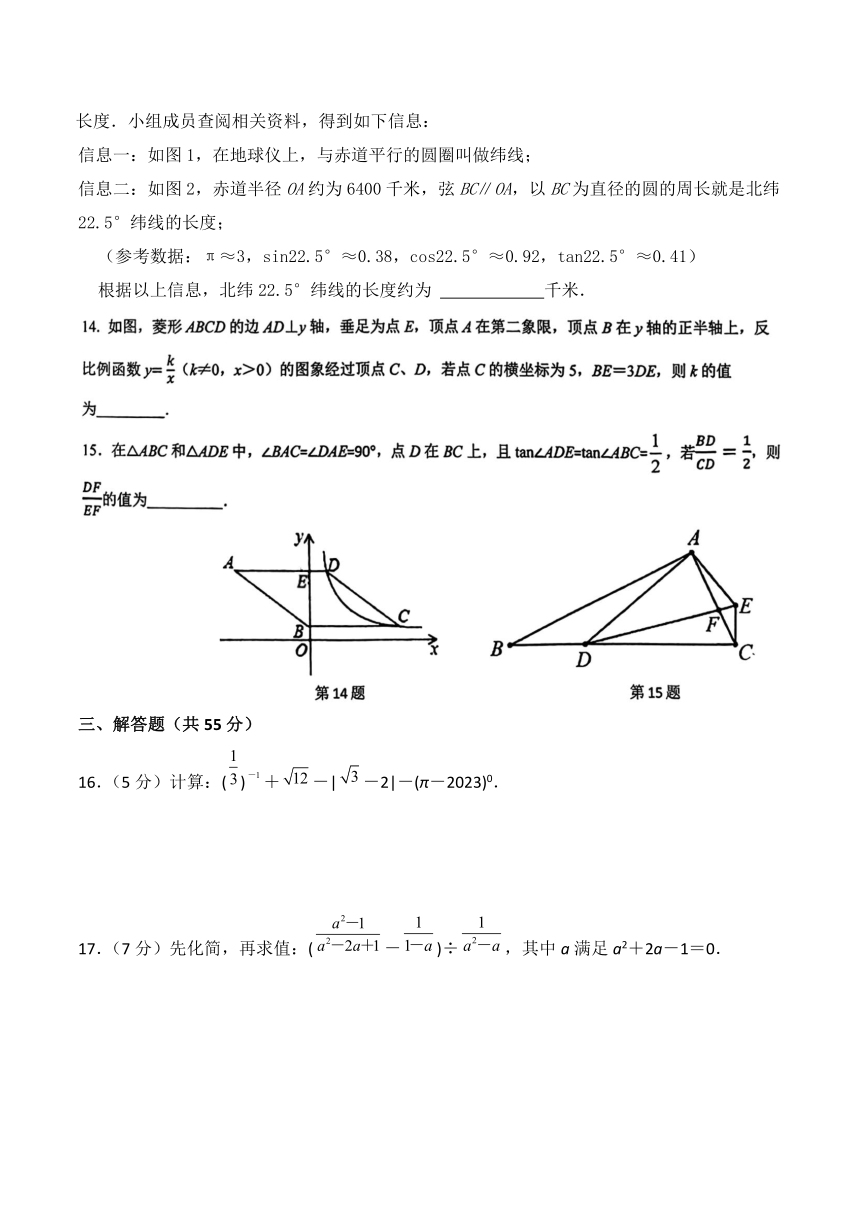
数学小组研究如下问题:深圳市的纬度约为北纬22.5°,求北纬22.5°纬线的
长度.小组成员查阅相关资料,得到如下信息:
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图2,赤道半径OA约为6400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬22.5°纬线的长度;
(参考数据:π≈3,sin22.5°≈0.38,cos22.5°≈0.92,tan22.5°≈0.41)
根据以上信息,北纬22.5°纬线的长度约为 千米.
三、解答题(共55分)
16.(5分)计算:()+-|-2|-(π-2023)0.
17.(7分)先化简,再求值:(-)÷,其中a满足a2+2a-1=0.
18.(7分)现在越来越多的孩子从小学习很多乐器,吉他就是很热门的一个,中国音乐协会为了了解国产吉他的品质(指板材质、发出的声音等),对敦煌、凤灵两种品牌进行了抽样调查。在相同条件下,随机抽取了两种品牌的吉他各9份样品,对吉他的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种品牌吉他得分的统计图表.
甲、乙两种品牌吉他得分表
序号 1 2 3 4 5 6 7 8 9
敦煌(分) 81 82 83 88 90 90 90 92 95
凤灵(分) 74 75 85 88 89 90 91 97 97
敦煌、凤灵两种吉他得分统计表
平均数 中位数 众数
敦煌 87.9 90 b
凤灵 87.3 a 97
(1)a= ,b= ;
(2)从方差的角度看, 种吉他的得分较稳定(填“敦煌”或“凤灵”);
(3)小明认为敦煌的吉他品质较好些,小军认为凤灵的吉他品质较好些.请结合统计图表中的信息分别写出他们的理由.
19.(8分)某新型高科技商品,每件的售价比进价多10元,8件的进价相当于6件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖4件。
(1)该商品的售价和进价分别是多少元?
(2) 设每天的销售利润为w元,但物价部门规定其销售单价不高于进价的1.8倍,则当告价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
20.(8分)如图,在△ABC中,AC=BC,以BC为直径作⊙O,交AC于点F,过C点作CD⊥AC交AB延长线于点D,E为CD上一点,且EB=ED.
(1)求证:BE为⊙O的切线;
(2)若AF=2,tanA=2,求BE的长.
21.(10分)在平面直角坐标系中,若两点的横坐标不相等,纵坐标互为相反数,则称这两点关于x轴斜对称.其中一点叫做另一点关于x轴的斜对称点.如:点(-4,2),(1,-2)关于x轴斜对称.在平面直角坐标系xOy中,点A的坐标为(2,1).
(1)下列各点中,与点A关于x轴斜对称的是 (只填序号);
①(3,-1),②(-2,1),③(2,-1),④(-1,-1).
(2)若点A关于x轴的斜对称点B恰好落在直线y=kx+1上,△AOB的面积为3,求k的值;
(3)抛物线y=x2-bx-1上恰有两个点M、N与点A关于x轴斜对称,抛物线的顶点为D,且△DMN为等腰直角三角形,则b的值为 .
22.在一节数学探究课中,同学们遇到这样的几何问题:如图1,等腰直角三角形ABC和ADE共顶点A,且A、C、D三点共线,∠ACB=∠ADE=90°,连接BE,G是BE的中点,连接CG和DG,请思考CG与DG具有怎样的数量和位置关系?
【模型构建】小颖提出CG=DG且CG⊥DG并给出了自己思考,以G是BE中点入手,如图2,通过延长CG与DE相交于点F,证明△BGC≌△EGF,得到BC=EF,随后通过AD-BC=DE-EF得AD-AC=DE-EF,即CD=FD,又CG=FG,所以CG⊥DG且CG=DG.
请结合小颖的证明思路利用结论填空:当AD=6,BC=3时,CG=__________;BE=____________.
【类比探究】(2)如图3,若将△ADE绕点A逆时针旋转度(0<<45),请分析此时上述结论是否成立?如果成立,请写出证明过程,如果不成立,请说明理由.
【拓展延伸】(3)若将△ADE绕点E逆时针旋转度(0<<360),当BG=CG时,请直接写出旋转角的度数为______________.
班级: 姓名:
一、选择题(共10小题,每小题3分,计30分)
1.下列互为倒数是( )
A.和 B.和-2 C.和-2 D.和
2.下面四个化学仪器示意图中,是轴对称图形的是( )
A. B. C. D.
3.深圳是改革开放后党和人民一手缔造的崭新城市,是中国特色社会主义在一张白纸上的精彩演绎。深圳广大干部群众披荆斩棘、埋头苦干,用40年的时间走过了国外一些国际大都市上百年走完的历程。深圳经济特区生机勃勃,向世界展示了我国改革开放的磅礴伟力,2022年深圳市年度GDP为32387万亿,用科学计数法表示2022年深圳GDP为( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C.( D.
5. 已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20°
B.30°
C.40°
D.50°
6.假如控制双眼皮的基因为A,控制单眼皮的基因为,(即基因为时,则为单眼皮)如图为一对夫妻的基因遗传图谱,则生一个孩子为双眼皮的概率为( )
A. B. C. D.
7. 下列命题错误的是( )
A.对角线相等的平行四边形是矩形 B.切线垂直于经过切点的半径
C.将一次函数图像向上平移1个单位得到的图像
有一组角相等及两边对应成比例的两个三角形相似
8.如图,在菱形ABCD中,AC=,∠ADC=120°,以点A
为圆心画圆弧交AC于点E,则阴影部分的面积为( )
A. B. C. D.
9. 我国古代数学名著九章算术中记载“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出钱,多出钱;每人出钱,还差钱.问人数、物价各是多少?若设共有人,物价是钱,则下列方程正确的是( )
A. B.
C. D.
10.如图,在矩形ABCD中,E为边AB上一点,将△ADE沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点G.若BF·AD=12,则AF的长度为( )
A.6 B.12
C. D.2
二、填空题(共5小题,每小题3分,计15分.)
11. 因式分解:=
12.如图,二次函数与x 轴交点坐标为(-1,0)(2,0)当y<0时,x 的取值范围是
数学小组研究如下问题:深圳市的纬度约为北纬22.5°,求北纬22.5°纬线的
长度.小组成员查阅相关资料,得到如下信息:
信息一:如图1,在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图2,赤道半径OA约为6400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬22.5°纬线的长度;
(参考数据:π≈3,sin22.5°≈0.38,cos22.5°≈0.92,tan22.5°≈0.41)
根据以上信息,北纬22.5°纬线的长度约为 千米.
三、解答题(共55分)
16.(5分)计算:()+-|-2|-(π-2023)0.
17.(7分)先化简,再求值:(-)÷,其中a满足a2+2a-1=0.
18.(7分)现在越来越多的孩子从小学习很多乐器,吉他就是很热门的一个,中国音乐协会为了了解国产吉他的品质(指板材质、发出的声音等),对敦煌、凤灵两种品牌进行了抽样调查。在相同条件下,随机抽取了两种品牌的吉他各9份样品,对吉他的品质进行评分(百分制),并对数据进行收集、整理,下面给出两种品牌吉他得分的统计图表.
甲、乙两种品牌吉他得分表
序号 1 2 3 4 5 6 7 8 9
敦煌(分) 81 82 83 88 90 90 90 92 95
凤灵(分) 74 75 85 88 89 90 91 97 97
敦煌、凤灵两种吉他得分统计表
平均数 中位数 众数
敦煌 87.9 90 b
凤灵 87.3 a 97
(1)a= ,b= ;
(2)从方差的角度看, 种吉他的得分较稳定(填“敦煌”或“凤灵”);
(3)小明认为敦煌的吉他品质较好些,小军认为凤灵的吉他品质较好些.请结合统计图表中的信息分别写出他们的理由.
19.(8分)某新型高科技商品,每件的售价比进价多10元,8件的进价相当于6件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖4件。
(1)该商品的售价和进价分别是多少元?
(2) 设每天的销售利润为w元,但物价部门规定其销售单价不高于进价的1.8倍,则当告价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
20.(8分)如图,在△ABC中,AC=BC,以BC为直径作⊙O,交AC于点F,过C点作CD⊥AC交AB延长线于点D,E为CD上一点,且EB=ED.
(1)求证:BE为⊙O的切线;
(2)若AF=2,tanA=2,求BE的长.
21.(10分)在平面直角坐标系中,若两点的横坐标不相等,纵坐标互为相反数,则称这两点关于x轴斜对称.其中一点叫做另一点关于x轴的斜对称点.如:点(-4,2),(1,-2)关于x轴斜对称.在平面直角坐标系xOy中,点A的坐标为(2,1).
(1)下列各点中,与点A关于x轴斜对称的是 (只填序号);
①(3,-1),②(-2,1),③(2,-1),④(-1,-1).
(2)若点A关于x轴的斜对称点B恰好落在直线y=kx+1上,△AOB的面积为3,求k的值;
(3)抛物线y=x2-bx-1上恰有两个点M、N与点A关于x轴斜对称,抛物线的顶点为D,且△DMN为等腰直角三角形,则b的值为 .
22.在一节数学探究课中,同学们遇到这样的几何问题:如图1,等腰直角三角形ABC和ADE共顶点A,且A、C、D三点共线,∠ACB=∠ADE=90°,连接BE,G是BE的中点,连接CG和DG,请思考CG与DG具有怎样的数量和位置关系?
【模型构建】小颖提出CG=DG且CG⊥DG并给出了自己思考,以G是BE中点入手,如图2,通过延长CG与DE相交于点F,证明△BGC≌△EGF,得到BC=EF,随后通过AD-BC=DE-EF得AD-AC=DE-EF,即CD=FD,又CG=FG,所以CG⊥DG且CG=DG.
请结合小颖的证明思路利用结论填空:当AD=6,BC=3时,CG=__________;BE=____________.
【类比探究】(2)如图3,若将△ADE绕点A逆时针旋转度(0<<45),请分析此时上述结论是否成立?如果成立,请写出证明过程,如果不成立,请说明理由.
【拓展延伸】(3)若将△ADE绕点E逆时针旋转度(0<<360),当BG=CG时,请直接写出旋转角的度数为______________.
同课章节目录
