4.2.1 第2课时 等差数列的判定与性质 课件(共38张PPT)
文档属性
| 名称 | 4.2.1 第2课时 等差数列的判定与性质 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1017.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-20 18:47:28 | ||
图片预览









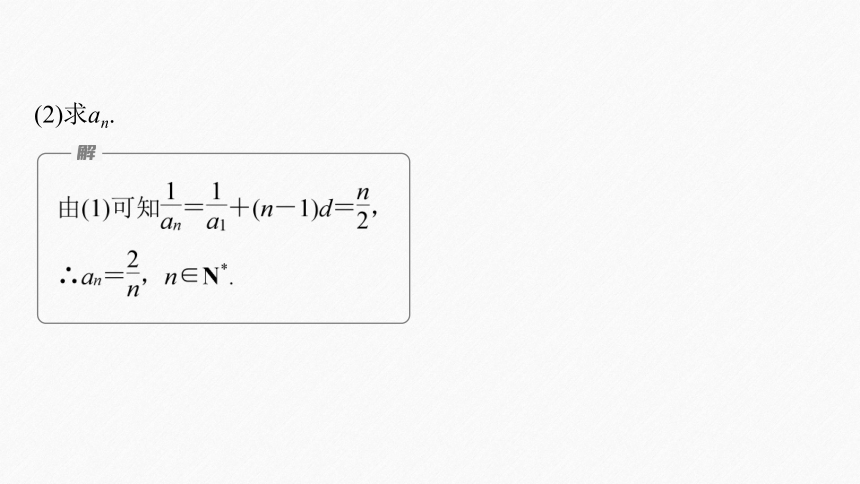

文档简介
(共38张PPT)
第2课时 等差数列的判定与性质
第四章 4.2.1 等差数列的概念
学习目标
1.掌握等差数列的判定与证明的方法.
2.掌握等差数列的性质及应用.
3.能根据实例抽象出等差数列进行简单的应用.
导语
当数列是等差数列时,可以根据公式进行一些计算,但对数列来说,如何判断是否为等差数列呢?
等差数列的判定与证明
一
问题1 如果一个数列的前有限项是等差数列,那么这个数列是等差数列吗?
提示 不一定,证明一个数列是等差数列,一定要体现出任意性.
知识梳理
证明或判定等差数列的方法
(1)定义法:an+1-an=d(n∈N*).
(2)等差中项法:2an=an-1+an+1(n≥2).
(3)通项公式法:an=a1+(n-1)d=pn+q(p,q为常数).
证明{an}是等差数列常用定义法.
注意点:
例1
(2)求an.
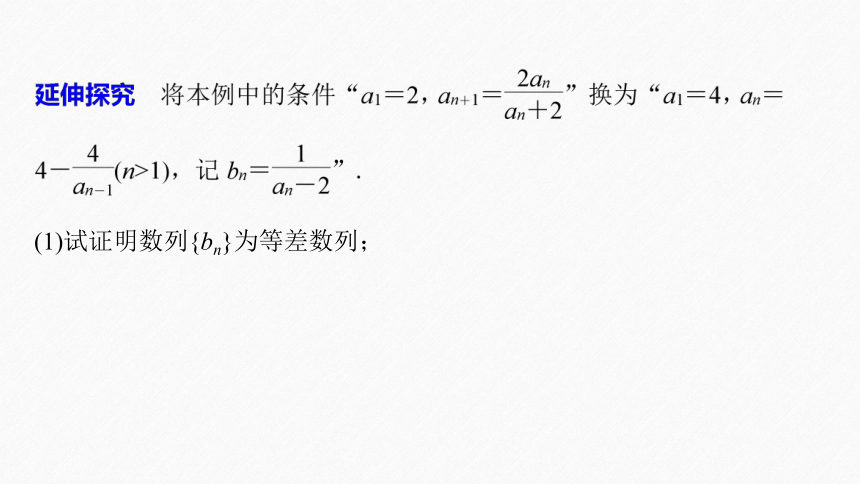
(1)试证明数列{bn}为等差数列;
(2)求数列{an}的通项公式.
判断等差数列的方法
(1)定义法
an+1-an=d(n∈N*)或an-an-1=d(n≥2,n∈N*) 数列{an}是等差数列.
(2)等差中项法
2an+1=an+an+2(n∈N*) 数列{an}为等差数列.
(3)通项公式法
数列{an}的通项公式形如an=pn+q(p,q为常数) 数列{an}为等差数列.
反思感悟
跟踪训练1
(1)证明:数列{bn}是等差数列;
(2)求数列{an}的通项公式.
等差数列的性质
二
问题2 如果{an}是等差数列,a3=5,d=2,如果不求首项,你能求数列的通项公式吗?
提示 由定义可知a3=a1+2d,an=a1+(n-1)d,两式相减得an-a3=(n-3)d,即an=a3+(n-3)d.
问题3 若数列{an}是等差数列,公差为d,m+n=p+q(m,n,p,q∈N*),则am,an,ap,aq这四项之间有什么样的关系?
提示 由等差数列的定义可知,am=a1+(m-1)d,an=a1+(n-1)d,ap=a1+(p-1)d,aq=a1+(q-1)d,容易发现am+an=2a1+(m+n-2)d,ap+aq=2a1+(p+q-2)d,因为m+n=p+q,故有am+an=ap+aq.
知识梳理
1.设等差数列{an}的首项为a1,公差为d,则
(1)an=dn+(a1-d)(n∈N*);
(2)an=am+________(m,n∈N*);
(3)d=_______(m,n∈N*,且m≠n).
2.下标性质:在等差数列{an}中,若m+n=p+q(m,n,p,q∈N*),则am+an=_______.
特别地,若m+n=2p(m,n,p∈N*),则有am+an=_____.
(n-m)d
ap+aq
2ap
(1)推广:若m+n+p=x+y+z,则am+an+ap=ax+ay+az.
(2)该性质要求下标的和相等,且左右两侧项数相同.
(3)在有穷等差数列中,与首末两项等距离的两项之和都相等,即a1+an=a2+an-1=….
注意点:
(1)已知{an}为等差数列,a15=8,a60=20,求a75.
例2
方法一 (利用an=am+(n-m)d)
设数列{an}的公差为d,
则a60=a15+(60-15)d=8+45d,
方法二 (利用隔项成等差数列)
因为{an}为等差数列,
所以a15,a30,a45,a60,a75也成等差数列,
设其公差为d,a15为首项,则a60为第四项,
所以a60=a15+3d,解得d=4,
所以a75=a60+d=24.
(2)已知数列{an}是等差数列,若a1-a9+a17=7,则a3+a15等于
A.7 B.14 C.21 D.7(n-1)
√
因为a1-a9+a17=(a1+a17)-a9=2a9-a9=a9=7,
所以a3+a15=2a9=2×7=14.
延伸探究 在等差数列{an}中,a3+a7+2a15=40,求a10.
方法一 设数列{an}的公差为d.
则a3+a7+2a15=a1+2d+a1+6d+2(a1+14d)
=4a1+36d=4(a1+9d)
=4a10=40,
∴a10=10.
方法二 ∵a3+a7+2a15=a3+a7+a15+a15=a10+a10+a10+a10=40,∴a10=10.
(1)灵活利用等差数列的性质,可以减少运算.令m=1,an=am+(n-m)d即变为an=a1+(n-1)d,可以减少记忆负担.
(2)等差数列运算的两种常用思路
①基本量法:根据已知条件,列出关于a1,d的方程(组),确定a1,d,然后求其他量.
②巧用性质法:观察等差数列中项的序号,若满足m+n=p+q=2r(m,n,p,q,r∈N*),
则am+an=ap+aq=2ar.
反思感悟
跟踪训练2
(1)已知{bn}为等差数列,若b3=-2,b10=12,则b8=____.
方法一 ∵{bn}为等差数列,∴可设其公差为d,
8
∴bn=b3+(n-3)d=2n-8.
∴b8=2×8-8=8.
(2)数列{an}满足3+an=an+1且a2+a4+a6=9,则log6(a5+a7+a9)的值是
√
由3+an=an+1,
得an+1-an=3.
所以{an}是公差为3的等差数列.
又a2+a4+a6=9,
且a2+a6=2a4,
所以3a4=9,
则a4=3,
所以a7=a4+3d=3+3×3=12,
故log6(a5+a7+a9)=log6(3a7)=log636=2.
由等差数列构造新数列
三
问题4 若数列{an}是等差数列,首项为a1,公差为d,在{an}中每相邻两项之间都插入4个数,若要使之构成一个新的等差数列,你能求出它的公差吗?
提示 设新数列为{ bn },公差为d′,则有b1=a1,b6=a2,所以b6-b1=a2-a1=d,故有5d′=d,所以d′= .
知识梳理
若{an},{bn}分别是公差为d,d′的等差数列,则有
数列 结论
{c+an} 公差为d的等差数列(c为任一常数)
{c·an} 公差为cd的等差数列(c为任一常数)
{an+an+k} 公差为2d的等差数列(k为常数,k∈N*)
{pan+qbn} 公差为pd+qd′的等差数列(p,q为常数)
有两个等差数列2,6,10,…,190和2,8,14,…,200,由这两个等差数列的公共项按从小到大的顺序组成一个新数列,则这个新数列的项数为
A.15 B.16 C.17 D.18
例3
√
易知,第一个数列的公差为4,第二个数列的公差为6,
故新数列的公差为具有相同首项的两个数列公差的最小公倍数,其公差为12,首项为2,
所以通项公式为an=12n-10,
而n∈N*,所以n的最大值为16.
对于任何形式的构造数列,判断是否为等差数列,一般从两个方面进行判断:
(1)定义:an-an-1是否为常数;(2)其通项公式是否为关于n的一次函数.
反思感悟
跟踪训练3
已知两个等差数列{an}:5,8,11,…,与{bn}:3,7,11,…,它们的公共项组成数列{cn},则数列{cn}的通项公式cn=________;若数列{an}和{bn}的项数均为100,则{cn}的项数是____.
由于数列{an}和{bn}都是等差数列,所以{cn}也是等差数列,且公差为3×4=12,又c1=11,故cn=11+12(n-1)=12n-1.
又a100=302,b100=399,所以11≤12n-1≤302,解得1≤n≤25.25,
又n∈N*,故{cn}的项数为25.
12n-1
25
课堂
小结
1.知识清单:
(1)证明等差数列的方法.
(2)等差数列的项与项之间的性质及应用.
(3)由等差数列构造新的数列.
2.方法归纳:定义法、公式法、构造法、解方程组法.
3.常见误区:
(1)不注意运用性质而出错或解法烦琐.
(2)实际问题中项数的确定.
第2课时 等差数列的判定与性质
第四章 4.2.1 等差数列的概念
学习目标
1.掌握等差数列的判定与证明的方法.
2.掌握等差数列的性质及应用.
3.能根据实例抽象出等差数列进行简单的应用.
导语
当数列是等差数列时,可以根据公式进行一些计算,但对数列来说,如何判断是否为等差数列呢?
等差数列的判定与证明
一
问题1 如果一个数列的前有限项是等差数列,那么这个数列是等差数列吗?
提示 不一定,证明一个数列是等差数列,一定要体现出任意性.
知识梳理
证明或判定等差数列的方法
(1)定义法:an+1-an=d(n∈N*).
(2)等差中项法:2an=an-1+an+1(n≥2).
(3)通项公式法:an=a1+(n-1)d=pn+q(p,q为常数).
证明{an}是等差数列常用定义法.
注意点:
例1
(2)求an.
(1)试证明数列{bn}为等差数列;
(2)求数列{an}的通项公式.
判断等差数列的方法
(1)定义法
an+1-an=d(n∈N*)或an-an-1=d(n≥2,n∈N*) 数列{an}是等差数列.
(2)等差中项法
2an+1=an+an+2(n∈N*) 数列{an}为等差数列.
(3)通项公式法
数列{an}的通项公式形如an=pn+q(p,q为常数) 数列{an}为等差数列.
反思感悟
跟踪训练1
(1)证明:数列{bn}是等差数列;
(2)求数列{an}的通项公式.
等差数列的性质
二
问题2 如果{an}是等差数列,a3=5,d=2,如果不求首项,你能求数列的通项公式吗?
提示 由定义可知a3=a1+2d,an=a1+(n-1)d,两式相减得an-a3=(n-3)d,即an=a3+(n-3)d.
问题3 若数列{an}是等差数列,公差为d,m+n=p+q(m,n,p,q∈N*),则am,an,ap,aq这四项之间有什么样的关系?
提示 由等差数列的定义可知,am=a1+(m-1)d,an=a1+(n-1)d,ap=a1+(p-1)d,aq=a1+(q-1)d,容易发现am+an=2a1+(m+n-2)d,ap+aq=2a1+(p+q-2)d,因为m+n=p+q,故有am+an=ap+aq.
知识梳理
1.设等差数列{an}的首项为a1,公差为d,则
(1)an=dn+(a1-d)(n∈N*);
(2)an=am+________(m,n∈N*);
(3)d=_______(m,n∈N*,且m≠n).
2.下标性质:在等差数列{an}中,若m+n=p+q(m,n,p,q∈N*),则am+an=_______.
特别地,若m+n=2p(m,n,p∈N*),则有am+an=_____.
(n-m)d
ap+aq
2ap
(1)推广:若m+n+p=x+y+z,则am+an+ap=ax+ay+az.
(2)该性质要求下标的和相等,且左右两侧项数相同.
(3)在有穷等差数列中,与首末两项等距离的两项之和都相等,即a1+an=a2+an-1=….
注意点:
(1)已知{an}为等差数列,a15=8,a60=20,求a75.
例2
方法一 (利用an=am+(n-m)d)
设数列{an}的公差为d,
则a60=a15+(60-15)d=8+45d,
方法二 (利用隔项成等差数列)
因为{an}为等差数列,
所以a15,a30,a45,a60,a75也成等差数列,
设其公差为d,a15为首项,则a60为第四项,
所以a60=a15+3d,解得d=4,
所以a75=a60+d=24.
(2)已知数列{an}是等差数列,若a1-a9+a17=7,则a3+a15等于
A.7 B.14 C.21 D.7(n-1)
√
因为a1-a9+a17=(a1+a17)-a9=2a9-a9=a9=7,
所以a3+a15=2a9=2×7=14.
延伸探究 在等差数列{an}中,a3+a7+2a15=40,求a10.
方法一 设数列{an}的公差为d.
则a3+a7+2a15=a1+2d+a1+6d+2(a1+14d)
=4a1+36d=4(a1+9d)
=4a10=40,
∴a10=10.
方法二 ∵a3+a7+2a15=a3+a7+a15+a15=a10+a10+a10+a10=40,∴a10=10.
(1)灵活利用等差数列的性质,可以减少运算.令m=1,an=am+(n-m)d即变为an=a1+(n-1)d,可以减少记忆负担.
(2)等差数列运算的两种常用思路
①基本量法:根据已知条件,列出关于a1,d的方程(组),确定a1,d,然后求其他量.
②巧用性质法:观察等差数列中项的序号,若满足m+n=p+q=2r(m,n,p,q,r∈N*),
则am+an=ap+aq=2ar.
反思感悟
跟踪训练2
(1)已知{bn}为等差数列,若b3=-2,b10=12,则b8=____.
方法一 ∵{bn}为等差数列,∴可设其公差为d,
8
∴bn=b3+(n-3)d=2n-8.
∴b8=2×8-8=8.
(2)数列{an}满足3+an=an+1且a2+a4+a6=9,则log6(a5+a7+a9)的值是
√
由3+an=an+1,
得an+1-an=3.
所以{an}是公差为3的等差数列.
又a2+a4+a6=9,
且a2+a6=2a4,
所以3a4=9,
则a4=3,
所以a7=a4+3d=3+3×3=12,
故log6(a5+a7+a9)=log6(3a7)=log636=2.
由等差数列构造新数列
三
问题4 若数列{an}是等差数列,首项为a1,公差为d,在{an}中每相邻两项之间都插入4个数,若要使之构成一个新的等差数列,你能求出它的公差吗?
提示 设新数列为{ bn },公差为d′,则有b1=a1,b6=a2,所以b6-b1=a2-a1=d,故有5d′=d,所以d′= .
知识梳理
若{an},{bn}分别是公差为d,d′的等差数列,则有
数列 结论
{c+an} 公差为d的等差数列(c为任一常数)
{c·an} 公差为cd的等差数列(c为任一常数)
{an+an+k} 公差为2d的等差数列(k为常数,k∈N*)
{pan+qbn} 公差为pd+qd′的等差数列(p,q为常数)
有两个等差数列2,6,10,…,190和2,8,14,…,200,由这两个等差数列的公共项按从小到大的顺序组成一个新数列,则这个新数列的项数为
A.15 B.16 C.17 D.18
例3
√
易知,第一个数列的公差为4,第二个数列的公差为6,
故新数列的公差为具有相同首项的两个数列公差的最小公倍数,其公差为12,首项为2,
所以通项公式为an=12n-10,
而n∈N*,所以n的最大值为16.
对于任何形式的构造数列,判断是否为等差数列,一般从两个方面进行判断:
(1)定义:an-an-1是否为常数;(2)其通项公式是否为关于n的一次函数.
反思感悟
跟踪训练3
已知两个等差数列{an}:5,8,11,…,与{bn}:3,7,11,…,它们的公共项组成数列{cn},则数列{cn}的通项公式cn=________;若数列{an}和{bn}的项数均为100,则{cn}的项数是____.
由于数列{an}和{bn}都是等差数列,所以{cn}也是等差数列,且公差为3×4=12,又c1=11,故cn=11+12(n-1)=12n-1.
又a100=302,b100=399,所以11≤12n-1≤302,解得1≤n≤25.25,
又n∈N*,故{cn}的项数为25.
12n-1
25
课堂
小结
1.知识清单:
(1)证明等差数列的方法.
(2)等差数列的项与项之间的性质及应用.
(3)由等差数列构造新的数列.
2.方法归纳:定义法、公式法、构造法、解方程组法.
3.常见误区:
(1)不注意运用性质而出错或解法烦琐.
(2)实际问题中项数的确定.
