4.3.1 第2课时 等比数列的判定与性质 课件(共43张PPT)
文档属性
| 名称 | 4.3.1 第2课时 等比数列的判定与性质 课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-20 18:50:39 | ||
图片预览






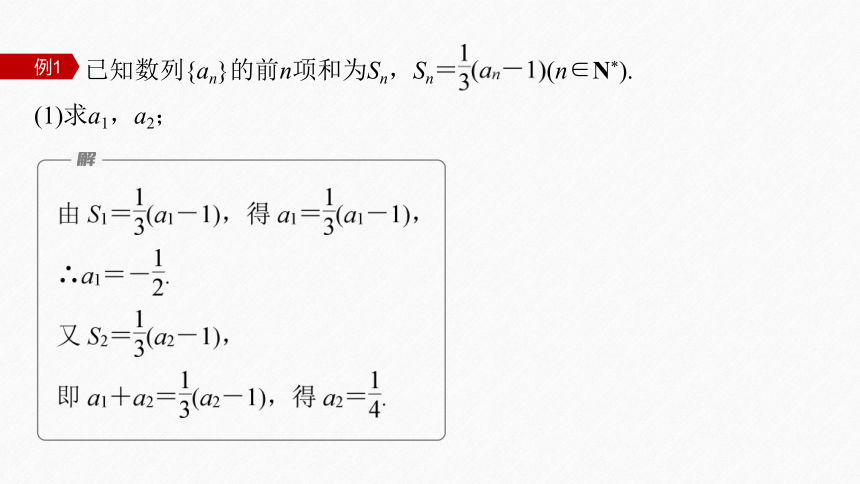





文档简介
(共43张PPT)
第2课时 等比数列的判定与性质
第四章 4.3.1 等比数列的概念
学习目标
1.掌握等比数列的判断及证明方法.
2.能根据等比数列的定义推出等比数列的性质,并能运用这些性质简化运算.
3.灵活应用等比数列通项公式的推广形式及变形.
等比数列的判定与证明
一
问题1 若数列{an}的前三项成等比数列,能说明这个数列是等比数列吗?
提示 不能,要证明一个数列是等比数列,一定要体现出任意性.
知识梳理
判定与证明等比数列的方法
1.定义法: =____(n∈N*且n≥2,q为不为0的常数);
2.等比中项法: =________(n∈N*且n≥2);
3.通项公式法:an=_______= =A·qn(A≠0).
q
an-1an+1
a1qn-1
(1)证明{an}为等比数列常用定义法.
注意点:
已知数列{an}的前n项和为Sn,Sn= (n∈N*).
(1)求a1,a2;
例1
(2)求证:数列{an}是等比数列.
当n≥2时,
判断一个数列是等比数列的常用方法
(2)通项公式法:若数列{an}的通项公式为an=a1qn-1(a1≠0,q≠0),则数列{an}是等比数列.
(3)等比中项法:若 =anan+2(n∈N*且an≠0),则数列{an}为等比数列.
反思感悟
跟踪训练1
得an>0,Sn>0.
得(n+2)Sn=n(Sn+1-Sn),
整理,得nSn+1=2(n+1)Sn,
等比数列中项与项之间的关系
二
问题2 结合上面的类比,你能把等差数列里面的an=am+(n-m)d类比出等比数列中相似的性质吗?
提示 类比可得an=amqn-m;由等比数列的定义可知an=a1qn-1,am=
a1qm-1,两式相除可得 =q(n-1)-(m-1)=qn-m,即an=amqn-m.
问题3 结合上面的类比,你能把等差数列里面的am+an=ak+al,类比出等比数列中相似的性质吗?
提示 类比可得aman=akal,其中m+n=k+l,m,n,k,l∈N*.
推导过程:am=a1qm-1,an=a1qn-1,ak=a1qk-1,al=a1ql-1,
因为m+n=k+l,所以有aman=akal.
知识梳理
1.等比数列通项公式的推广和变形an=_______.
2.设数列{an}为等比数列,则:
(1)若k+l=m+n(k,l,m,n∈N*),则____________.
(2)若m,p,n成等差数列,则__________成等比数列.
amqn-m
ak·al=am·an
am,ap,an
(1)性质的推广:若m+n+p=x+y+z,有amanap=axayaz.
(2)该性质要求下标的和相等,且左右两侧项数相同.
(3)在有穷等比数列中,与首末两项等距离的两项之积都相等,即a1·an=a2·an-1=….
注意点:
(1)在等比数列{an}中:
①已知a3+a6=36,a4+a7=18,an= ,求n;
例2
设等比数列{an}的公比为q.
再由a3+a6=a3·(1+q3)=36得a3=32,
所以n-8=1,所以n=9.
②已知a5=8,a7=2,an>0,求an.
(2)已知{an}为等比数列.
在等比数列{an}中,
②若an>0,a5a7+2a6a8+a6a10=49,求a6+a8;
由等比中项,化简条件得
即(a6+a8)2=49,
∵an>0,
∴a6+a8=7.
③若an>0,a5a6=9,求log3a1+log3a2+…+log3a10的值.
由等比数列的性质知a5a6=a1a10=a2a9=a3a8=a4a7=9,
∴log3a1+log3a2+…+log3a10=log3(a1a2·…·a10)
=log3[(a1a10)(a2a9)(a3a8)(a4a7)(a5a6)]
=log395=10.
(3)有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.
所以a3=216.
所以a=6.
由题意知第4个数为12q-6.
所以6+6q+12q-6=12,
故所求的四个数为9,6,4,2.
方法二 设后三个数为4-d,4,4+d,
解得4-d=6.
所以d=-2.
故所求得的四个数为9,6,4,2.
(1)等比数列的通项公式及变形的应用
①在已知等比数列的首项和公比的前提下,利用通项公式an=a1qn-1(a1q≠0)可求出等比数列中的任意一项.
②在已知等比数列中任意两项的前提下,利用an=amqn-m(q≠0)也可求出等比数列中的任意一项.
反思感悟
(2)利用等比数列的性质解题
①基本思路:充分发挥项的“下标”的指导作用,分析等比数列项与项之间的关系,选择恰当的性质解题.
②优缺点:简便快捷,但是适用面窄,有一定的思维含量.
反思感悟
反思感悟
(3)几个数成等比数列的设法
②四个符号相同的数成等比数列设为
反思感悟
推广到一般:偶数个符号相同的数成等比数列设为
③四个数成等比数列,不能确定它们的符号是否相同时,可设为a,aq,aq2,aq3.
跟踪训练2
(1)已知等比数列{an}满足a1+a5+a9=21,a4+a8+a12= ,则a7等于
A.4 B.8 C.16 D.32
设数列{an}的公比为q,
则a4+a8+a12=(a1+a5+a9)q3,
√
因为a1+a5+a9=a1(1+q4+q8)=21a1=21,
所以a1=1,则a7=a1q6=8.
√
因为a1,a13是方程x2-13x+9=0的两根,
所以a1a13=9,a1+a13=13,
所以a1>0,a13>0,
又{an}为等比数列,
则a7=a1q6>0,
所以a7=3或a7=-3(舍去),
(3)有四个数成等比数列,将这四个数分别减去1,1,4,13成等差数列,则这四个数的和是_____.
设这四个数分别为a,aq,aq2,aq3,
则a-1,aq-1,aq2-4,aq3-13成等差数列.
45
因此这四个数分别是3,6,12,24,其和为45.
由等比数列构造新等比数列
三
问题4 结合我们所学,你能类比等差数列、等比数列的通项公式的结构特点及运算关系吗?
提示
等差数列 等比数列
定义 如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列 如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列
符号表示 an-an-1=d(n≥2,n∈N*)
通项公式 an=a1+(n-1)d an=a1qn-1
类比 差 商;和 积,积 乘方
性质 等差数列首项a1,公差d 等比数列首项a1,公比q
把等差数列前k项去掉,得到一个以ak+1为首项,以d为公差的等差数列 把等比数列前k项去掉,得到一个以ak+1为首项,以q公比的等比数列
等差数列中,ak,ak+m,ak+2m…是以公差为md的等差数列 等比数列中,ak,ak+m,ak+2m…是以公比为qm的等比数列
等差数列中任意一项加上同一个常数,构成一个公差不变的等差数列 等比数列中任意一项同乘一个非零常数,构成一个公比不变的等比数列
两个等差数列相加,还是一个等差数列 两个等比数列相乘,还是一个等比数列
知识梳理
1.在等比数列{an}中,每隔k项(k∈N*)取出一项,按原来的顺序排列,所得的新数列仍为等比数列.
2.若{an}是等比数列,公比为q,则数列{λan}(λ≠0), 都是等比
数列,且公比分别是_________.
3.若{an},{bn}是项数相同的等比数列,公比分别是p和q,那么{anbn}与
也都是等比数列,公比分别为____和_____.
pq
在构造新的等比数列时,要注意新数列中有的项是否为0,比如公比q=-1时,连续相邻偶数项的和都是0,故不能构成等比数列.
注意点:
如果数列{an}是等比数列,那么下列数列中不一定是等比数列的是
例3
√
取等比数列an=(-1)n,则an+an+1=0,所以{an+an+1}不是等比数列,故D错误;
对于其他选项,均满足等比数列通项公式的性质.
由等比数列构造新的等比数列,一定要检验新的数列中的项是否为0,主要是针对q<0的情况.
反思感悟
跟踪训练3
设{an}是各项为正数的无穷数列,Ai是边长为ai,ai+1的矩形面积(i=1,2,…),则{An}为等比数列的充要条件为
A.{an}是等比数列
B.a1,a3,…,a2n-1,…或a2,a4,…,a2n,…是等比数列
C.a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列
D.a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比
相同
√
因为Ai是边长为ai,ai+1的矩形面积(i=1,2,…),所以Ai=aiai+1(i=1,2,3,…,n,…),
则数列{An}的通项为An=anan+1.根据等比数列的定义,
课堂
小结
1.知识清单:
(1)等比数列的判定与证明.
(2)等比数列项与项之间的关系及应用.
(3)由等比数列构造新的等比数列.
2.方法归纳:公式法、类比法、定义法、分类讨论法.
3.常见误区:
(1)构造新的等比数列易忽视有等于0的项.
(2)四个数成等比数列时设成 aq,aq3,未考虑公比为负的情况.
第2课时 等比数列的判定与性质
第四章 4.3.1 等比数列的概念
学习目标
1.掌握等比数列的判断及证明方法.
2.能根据等比数列的定义推出等比数列的性质,并能运用这些性质简化运算.
3.灵活应用等比数列通项公式的推广形式及变形.
等比数列的判定与证明
一
问题1 若数列{an}的前三项成等比数列,能说明这个数列是等比数列吗?
提示 不能,要证明一个数列是等比数列,一定要体现出任意性.
知识梳理
判定与证明等比数列的方法
1.定义法: =____(n∈N*且n≥2,q为不为0的常数);
2.等比中项法: =________(n∈N*且n≥2);
3.通项公式法:an=_______= =A·qn(A≠0).
q
an-1an+1
a1qn-1
(1)证明{an}为等比数列常用定义法.
注意点:
已知数列{an}的前n项和为Sn,Sn= (n∈N*).
(1)求a1,a2;
例1
(2)求证:数列{an}是等比数列.
当n≥2时,
判断一个数列是等比数列的常用方法
(2)通项公式法:若数列{an}的通项公式为an=a1qn-1(a1≠0,q≠0),则数列{an}是等比数列.
(3)等比中项法:若 =anan+2(n∈N*且an≠0),则数列{an}为等比数列.
反思感悟
跟踪训练1
得an>0,Sn>0.
得(n+2)Sn=n(Sn+1-Sn),
整理,得nSn+1=2(n+1)Sn,
等比数列中项与项之间的关系
二
问题2 结合上面的类比,你能把等差数列里面的an=am+(n-m)d类比出等比数列中相似的性质吗?
提示 类比可得an=amqn-m;由等比数列的定义可知an=a1qn-1,am=
a1qm-1,两式相除可得 =q(n-1)-(m-1)=qn-m,即an=amqn-m.
问题3 结合上面的类比,你能把等差数列里面的am+an=ak+al,类比出等比数列中相似的性质吗?
提示 类比可得aman=akal,其中m+n=k+l,m,n,k,l∈N*.
推导过程:am=a1qm-1,an=a1qn-1,ak=a1qk-1,al=a1ql-1,
因为m+n=k+l,所以有aman=akal.
知识梳理
1.等比数列通项公式的推广和变形an=_______.
2.设数列{an}为等比数列,则:
(1)若k+l=m+n(k,l,m,n∈N*),则____________.
(2)若m,p,n成等差数列,则__________成等比数列.
amqn-m
ak·al=am·an
am,ap,an
(1)性质的推广:若m+n+p=x+y+z,有amanap=axayaz.
(2)该性质要求下标的和相等,且左右两侧项数相同.
(3)在有穷等比数列中,与首末两项等距离的两项之积都相等,即a1·an=a2·an-1=….
注意点:
(1)在等比数列{an}中:
①已知a3+a6=36,a4+a7=18,an= ,求n;
例2
设等比数列{an}的公比为q.
再由a3+a6=a3·(1+q3)=36得a3=32,
所以n-8=1,所以n=9.
②已知a5=8,a7=2,an>0,求an.
(2)已知{an}为等比数列.
在等比数列{an}中,
②若an>0,a5a7+2a6a8+a6a10=49,求a6+a8;
由等比中项,化简条件得
即(a6+a8)2=49,
∵an>0,
∴a6+a8=7.
③若an>0,a5a6=9,求log3a1+log3a2+…+log3a10的值.
由等比数列的性质知a5a6=a1a10=a2a9=a3a8=a4a7=9,
∴log3a1+log3a2+…+log3a10=log3(a1a2·…·a10)
=log3[(a1a10)(a2a9)(a3a8)(a4a7)(a5a6)]
=log395=10.
(3)有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.
所以a3=216.
所以a=6.
由题意知第4个数为12q-6.
所以6+6q+12q-6=12,
故所求的四个数为9,6,4,2.
方法二 设后三个数为4-d,4,4+d,
解得4-d=6.
所以d=-2.
故所求得的四个数为9,6,4,2.
(1)等比数列的通项公式及变形的应用
①在已知等比数列的首项和公比的前提下,利用通项公式an=a1qn-1(a1q≠0)可求出等比数列中的任意一项.
②在已知等比数列中任意两项的前提下,利用an=amqn-m(q≠0)也可求出等比数列中的任意一项.
反思感悟
(2)利用等比数列的性质解题
①基本思路:充分发挥项的“下标”的指导作用,分析等比数列项与项之间的关系,选择恰当的性质解题.
②优缺点:简便快捷,但是适用面窄,有一定的思维含量.
反思感悟
反思感悟
(3)几个数成等比数列的设法
②四个符号相同的数成等比数列设为
反思感悟
推广到一般:偶数个符号相同的数成等比数列设为
③四个数成等比数列,不能确定它们的符号是否相同时,可设为a,aq,aq2,aq3.
跟踪训练2
(1)已知等比数列{an}满足a1+a5+a9=21,a4+a8+a12= ,则a7等于
A.4 B.8 C.16 D.32
设数列{an}的公比为q,
则a4+a8+a12=(a1+a5+a9)q3,
√
因为a1+a5+a9=a1(1+q4+q8)=21a1=21,
所以a1=1,则a7=a1q6=8.
√
因为a1,a13是方程x2-13x+9=0的两根,
所以a1a13=9,a1+a13=13,
所以a1>0,a13>0,
又{an}为等比数列,
则a7=a1q6>0,
所以a7=3或a7=-3(舍去),
(3)有四个数成等比数列,将这四个数分别减去1,1,4,13成等差数列,则这四个数的和是_____.
设这四个数分别为a,aq,aq2,aq3,
则a-1,aq-1,aq2-4,aq3-13成等差数列.
45
因此这四个数分别是3,6,12,24,其和为45.
由等比数列构造新等比数列
三
问题4 结合我们所学,你能类比等差数列、等比数列的通项公式的结构特点及运算关系吗?
提示
等差数列 等比数列
定义 如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列 如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列
符号表示 an-an-1=d(n≥2,n∈N*)
通项公式 an=a1+(n-1)d an=a1qn-1
类比 差 商;和 积,积 乘方
性质 等差数列首项a1,公差d 等比数列首项a1,公比q
把等差数列前k项去掉,得到一个以ak+1为首项,以d为公差的等差数列 把等比数列前k项去掉,得到一个以ak+1为首项,以q公比的等比数列
等差数列中,ak,ak+m,ak+2m…是以公差为md的等差数列 等比数列中,ak,ak+m,ak+2m…是以公比为qm的等比数列
等差数列中任意一项加上同一个常数,构成一个公差不变的等差数列 等比数列中任意一项同乘一个非零常数,构成一个公比不变的等比数列
两个等差数列相加,还是一个等差数列 两个等比数列相乘,还是一个等比数列
知识梳理
1.在等比数列{an}中,每隔k项(k∈N*)取出一项,按原来的顺序排列,所得的新数列仍为等比数列.
2.若{an}是等比数列,公比为q,则数列{λan}(λ≠0), 都是等比
数列,且公比分别是_________.
3.若{an},{bn}是项数相同的等比数列,公比分别是p和q,那么{anbn}与
也都是等比数列,公比分别为____和_____.
pq
在构造新的等比数列时,要注意新数列中有的项是否为0,比如公比q=-1时,连续相邻偶数项的和都是0,故不能构成等比数列.
注意点:
如果数列{an}是等比数列,那么下列数列中不一定是等比数列的是
例3
√
取等比数列an=(-1)n,则an+an+1=0,所以{an+an+1}不是等比数列,故D错误;
对于其他选项,均满足等比数列通项公式的性质.
由等比数列构造新的等比数列,一定要检验新的数列中的项是否为0,主要是针对q<0的情况.
反思感悟
跟踪训练3
设{an}是各项为正数的无穷数列,Ai是边长为ai,ai+1的矩形面积(i=1,2,…),则{An}为等比数列的充要条件为
A.{an}是等比数列
B.a1,a3,…,a2n-1,…或a2,a4,…,a2n,…是等比数列
C.a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列
D.a1,a3,…,a2n-1,…和a2,a4,…,a2n,…均是等比数列,且公比
相同
√
因为Ai是边长为ai,ai+1的矩形面积(i=1,2,…),所以Ai=aiai+1(i=1,2,3,…,n,…),
则数列{An}的通项为An=anan+1.根据等比数列的定义,
课堂
小结
1.知识清单:
(1)等比数列的判定与证明.
(2)等比数列项与项之间的关系及应用.
(3)由等比数列构造新的等比数列.
2.方法归纳:公式法、类比法、定义法、分类讨论法.
3.常见误区:
(1)构造新的等比数列易忽视有等于0的项.
(2)四个数成等比数列时设成 aq,aq3,未考虑公比为负的情况.
