福建省南平市武夷山市2022-2023学年九年级下学期6月月考数学试题(无答案)
文档属性
| 名称 | 福建省南平市武夷山市2022-2023学年九年级下学期6月月考数学试题(无答案) | 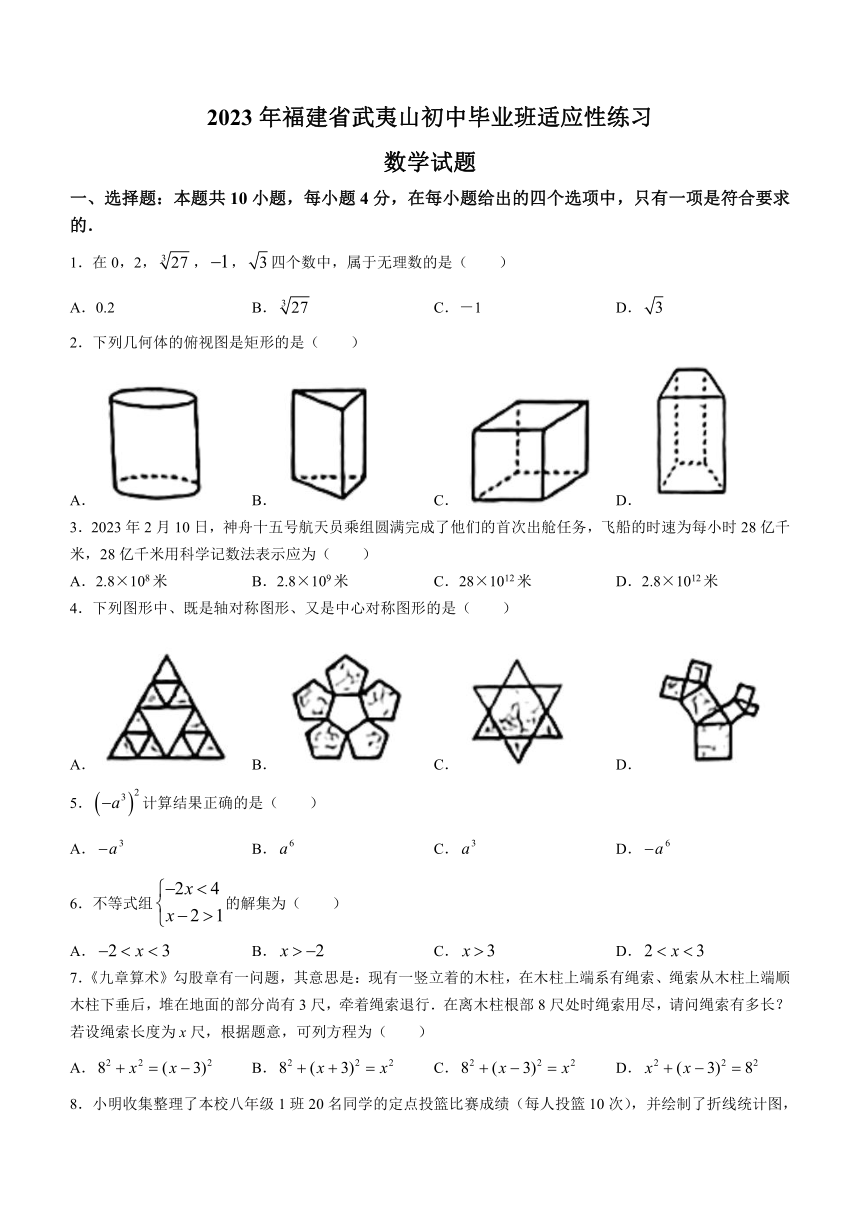 | |
| 格式 | docx | ||
| 文件大小 | 619.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 19:09:08 | ||
图片预览



文档简介
2023年福建省武夷山初中毕业班适应性练习
数学试题
一、选择题:本题共10小题,每小题4分,在每小题给出的四个选项中,只有一项是符合要求的.
1.在0,2,,,四个数中,属于无理数的是( )
A.0.2 B. C.-1 D.
2.下列几何体的俯视图是矩形的是( )
A. B. C. D.
3.2023年2月10日,神舟十五号航天员乘组圆满完成了他们的首次出舱任务,飞船的时速为每小时28亿千米,28亿千米用科学记数法表示应为( )
A.2.8×108米 B.2.8×109米 C.28×1012米 D.2.8×1012米
4.下列图形中、既是轴对称图形、又是中心对称图形的是( )
A. B. C. D.
5.计算结果正确的是( )
A. B. C. D.
6.不等式组的解集为( )
A. B. C. D.
7.《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索、绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行.在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为( )
A. B. C. D.
8.小明收集整理了本校八年级1班20名同学的定点投篮比赛成绩(每人投篮10次),并绘制了折线统计图,如图所示,那么这次比赛成绩的中位数、众数分别是( )
A.6,7 B.7,7 C.5,8 D.7,8
9.如图,一枚运载火箭从地面L处发射,雷达站R与发射点L距离6km,当火箭到达A点时、雷达站测得仰角为43°,则这枚火箭此时的高度AL为( )
A. B. C. D.
10.如图,在平面直角坐标系中,点都在二次函数的图象上.若,则的取值范围是( )
A. B. C. D.
二、填空题:本题共6小题,每小题4分,共24分.
11.分解因式:a3-a=_________________.
12.大小、形状完全相同的5张卡片、背面分别写着“我”“的”“中”“国”“梦”这5个字,从中随机抽取一张,则这张卡片背面恰好写着“中”字的概率是_________________.
13.如图,在△ABC中,AB=13,BC=12,点D、E分别是AB,BC的中点,连接DE、CD,如果DE=2.5,那么△ABC的周长是_________________.
14.若点都在反比例函数(为常数)的图象上,则的大小关系为_________________.
15.某校举行一次数学竞赛、赛后5名同学A,B,C,D,E知道了自己的成绩,但这5名学生想尽快得知比赛的名次,得到如下信息:
信息序号 文字信息
1 的得分是得分的四分之一
2 的得分是得分的3倍
3 和的得分之和等于和的总分
t 与的得分之差是得分的四分之三
则这5位同学中获得第三名的是_________________.
16.如图,正方形ABCD的边长为1,点E是BC上一动点(不与点B,C重合),过点E作EF⊥AE交正方形外角的平分线CF于点F,交CD于点G,连接AF,下列结论:①AE=EF;②;③∠DAF=∠CEF,④△CEF的面积的最大值为.其中正确的是_________________.(填写正确结论的序号)
三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.
17.(8分)计算:.
18.(8分)如图、已知在△ABC中,点D为BC边上一点,∠B=∠4,∠1=∠2=∠3,求证:BC=DE.
19.(8分)先化简:,然后从的范围内选取一个合适的整数作为的值代入求值.
20.(8分)自共享单车上市以来,给人们的出行提供了便利,受到了广大市民的青睐,某公司为了了解员工上下班回家的路线(设路程为x公里)情况,随机抽取了若干名员工进行了问卷调查,现将这些员工的调查结果分为四个等级.A:0≤x≤3、B:3<x≤6、C:6<x≤9、D:x>9,并将调查结果绘制成如下两个不完整的统计图.
(1)补全上面的条形统计图和扇形统计图,其中扇形统计图中a=_________________,b=_________________;
(2)所抽取员工下班路程的中位数落在等级_________________(填字母);
(3)若该公司有900名员工,在高峰期时路程在6公里以下的员工会优先选择共享单车下班,请你估算该公司有多少人会优先选择共享单车.
21.(8分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
(1)求证:BE=CE;
(2)若AB=6,∠BAC=54°,求的长.
22.(10分)某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用1200元购买B款保温杯的数量与用960元购买A款保温杯的数量相同.
(1)A、B两款保温杯销售单价各是多少元?
(2)由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的一半,A款保温杯的进价为每个30元,B款保温杯的进价为每个35元,若两款保温杯的销售单价不变,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
23.(10分)如图.已知、∠ABC=120°,点E为线段BC上的一点、连接AE.
(1)将线段AE绕点A逆时针旋转60°得到线段AF,点E的对应点是点F,请用尺规作图作出线段AF(保留作图痕迹,不写作法);
(2)在(1)的条作下,求证:点F在∠ABC的平分线上.
24.(12分)在△ABC和△ADE中,AB=AC、AD=AE.∠BAC=∠DAE,连接CE.
(1)如图1,若点D在BC边上,AC,DE相交于点F.
①求证:BD=CE;
②若AF=DF,AB=5,BC=6,求BD的长.
(2)如图2,若∠BAC=90°,M为BE的中点,连接AM,求证:AM⊥CD.
25.(14分)如图,直线分别交轴,轴于点,抛物线过,两点,其顶点为,对称轴与直线交于点N.
(1)直接写出抛物线的解析式;
(2)如图1,点是线段上一动点,过点作轴于点,交抛物线于点,问:是否存在点,使四边形为菱形?并说明理由;
(3)如图2,点为轴负半轴上的一动点,过点作,直线与拋物线交于点,与直线交于点,若,求点的坐标.
数学试题
一、选择题:本题共10小题,每小题4分,在每小题给出的四个选项中,只有一项是符合要求的.
1.在0,2,,,四个数中,属于无理数的是( )
A.0.2 B. C.-1 D.
2.下列几何体的俯视图是矩形的是( )
A. B. C. D.
3.2023年2月10日,神舟十五号航天员乘组圆满完成了他们的首次出舱任务,飞船的时速为每小时28亿千米,28亿千米用科学记数法表示应为( )
A.2.8×108米 B.2.8×109米 C.28×1012米 D.2.8×1012米
4.下列图形中、既是轴对称图形、又是中心对称图形的是( )
A. B. C. D.
5.计算结果正确的是( )
A. B. C. D.
6.不等式组的解集为( )
A. B. C. D.
7.《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索、绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行.在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x尺,根据题意,可列方程为( )
A. B. C. D.
8.小明收集整理了本校八年级1班20名同学的定点投篮比赛成绩(每人投篮10次),并绘制了折线统计图,如图所示,那么这次比赛成绩的中位数、众数分别是( )
A.6,7 B.7,7 C.5,8 D.7,8
9.如图,一枚运载火箭从地面L处发射,雷达站R与发射点L距离6km,当火箭到达A点时、雷达站测得仰角为43°,则这枚火箭此时的高度AL为( )
A. B. C. D.
10.如图,在平面直角坐标系中,点都在二次函数的图象上.若,则的取值范围是( )
A. B. C. D.
二、填空题:本题共6小题,每小题4分,共24分.
11.分解因式:a3-a=_________________.
12.大小、形状完全相同的5张卡片、背面分别写着“我”“的”“中”“国”“梦”这5个字,从中随机抽取一张,则这张卡片背面恰好写着“中”字的概率是_________________.
13.如图,在△ABC中,AB=13,BC=12,点D、E分别是AB,BC的中点,连接DE、CD,如果DE=2.5,那么△ABC的周长是_________________.
14.若点都在反比例函数(为常数)的图象上,则的大小关系为_________________.
15.某校举行一次数学竞赛、赛后5名同学A,B,C,D,E知道了自己的成绩,但这5名学生想尽快得知比赛的名次,得到如下信息:
信息序号 文字信息
1 的得分是得分的四分之一
2 的得分是得分的3倍
3 和的得分之和等于和的总分
t 与的得分之差是得分的四分之三
则这5位同学中获得第三名的是_________________.
16.如图,正方形ABCD的边长为1,点E是BC上一动点(不与点B,C重合),过点E作EF⊥AE交正方形外角的平分线CF于点F,交CD于点G,连接AF,下列结论:①AE=EF;②;③∠DAF=∠CEF,④△CEF的面积的最大值为.其中正确的是_________________.(填写正确结论的序号)
三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.
17.(8分)计算:.
18.(8分)如图、已知在△ABC中,点D为BC边上一点,∠B=∠4,∠1=∠2=∠3,求证:BC=DE.
19.(8分)先化简:,然后从的范围内选取一个合适的整数作为的值代入求值.
20.(8分)自共享单车上市以来,给人们的出行提供了便利,受到了广大市民的青睐,某公司为了了解员工上下班回家的路线(设路程为x公里)情况,随机抽取了若干名员工进行了问卷调查,现将这些员工的调查结果分为四个等级.A:0≤x≤3、B:3<x≤6、C:6<x≤9、D:x>9,并将调查结果绘制成如下两个不完整的统计图.
(1)补全上面的条形统计图和扇形统计图,其中扇形统计图中a=_________________,b=_________________;
(2)所抽取员工下班路程的中位数落在等级_________________(填字母);
(3)若该公司有900名员工,在高峰期时路程在6公里以下的员工会优先选择共享单车下班,请你估算该公司有多少人会优先选择共享单车.
21.(8分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
(1)求证:BE=CE;
(2)若AB=6,∠BAC=54°,求的长.
22.(10分)某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用1200元购买B款保温杯的数量与用960元购买A款保温杯的数量相同.
(1)A、B两款保温杯销售单价各是多少元?
(2)由于需求量大,A、B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的一半,A款保温杯的进价为每个30元,B款保温杯的进价为每个35元,若两款保温杯的销售单价不变,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
23.(10分)如图.已知、∠ABC=120°,点E为线段BC上的一点、连接AE.
(1)将线段AE绕点A逆时针旋转60°得到线段AF,点E的对应点是点F,请用尺规作图作出线段AF(保留作图痕迹,不写作法);
(2)在(1)的条作下,求证:点F在∠ABC的平分线上.
24.(12分)在△ABC和△ADE中,AB=AC、AD=AE.∠BAC=∠DAE,连接CE.
(1)如图1,若点D在BC边上,AC,DE相交于点F.
①求证:BD=CE;
②若AF=DF,AB=5,BC=6,求BD的长.
(2)如图2,若∠BAC=90°,M为BE的中点,连接AM,求证:AM⊥CD.
25.(14分)如图,直线分别交轴,轴于点,抛物线过,两点,其顶点为,对称轴与直线交于点N.
(1)直接写出抛物线的解析式;
(2)如图1,点是线段上一动点,过点作轴于点,交抛物线于点,问:是否存在点,使四边形为菱形?并说明理由;
(3)如图2,点为轴负半轴上的一动点,过点作,直线与拋物线交于点,与直线交于点,若,求点的坐标.
同课章节目录
