上海2022-2023学年七年级下学期期末数学试题(无答案)
文档属性
| 名称 | 上海2022-2023学年七年级下学期期末数学试题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 468.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 00:00:00 | ||
图片预览

文档简介
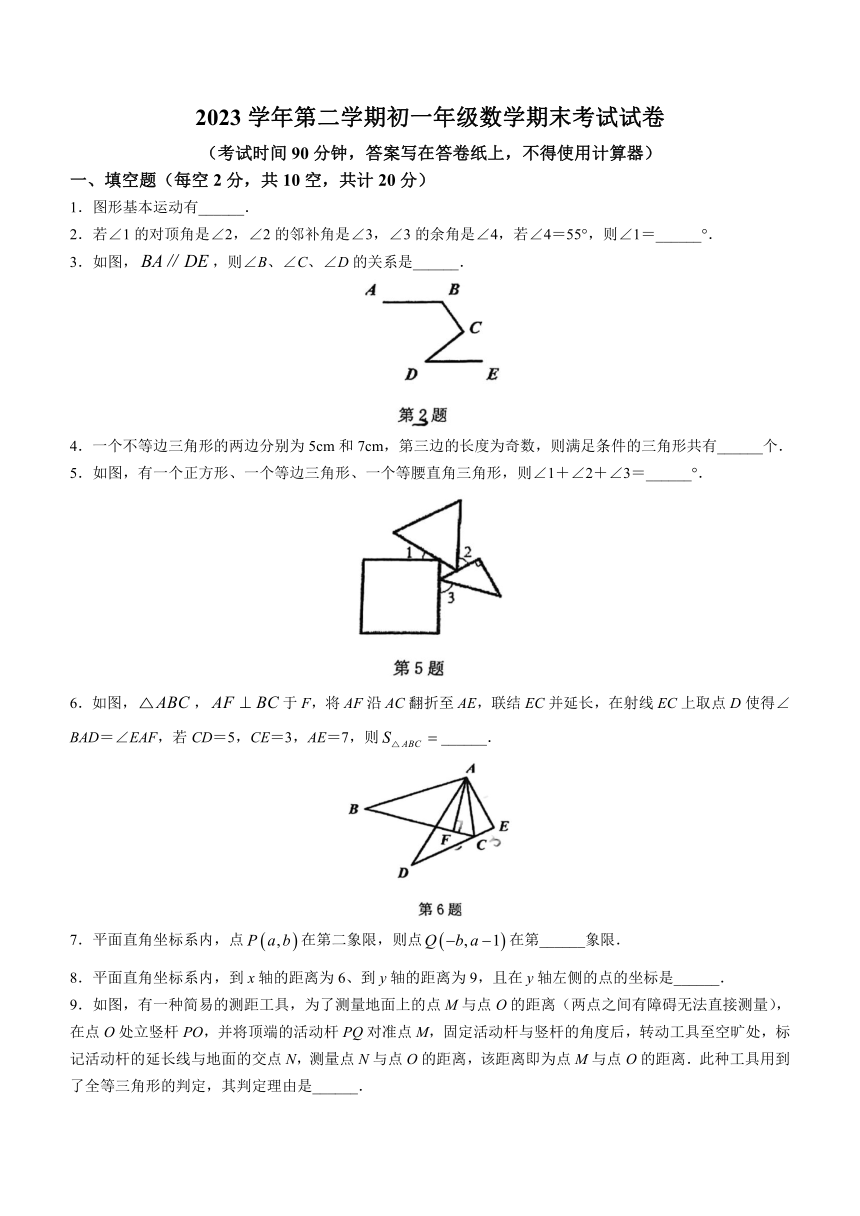
2023学年第二学期初一年级数学期末考试试卷
(考试时间90分钟,答案写在答卷纸上,不得使用计算器)
一、填空题(每空2分,共10空,共计20分)
1.图形基本运动有______.
2.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3的余角是∠4,若∠4=55°,则∠1=______°.
3.如图,,则∠B、∠C、∠D的关系是______.
4.一个不等边三角形的两边分别为5cm和7cm,第三边的长度为奇数,则满足条件的三角形共有______个.
5.如图,有一个正方形、一个等边三角形、一个等腰直角三角形,则∠1+∠2+∠3=______°.
6.如图,,于F,将AF沿AC翻折至AE,联结EC并延长,在射线EC上取点D使得∠BAD=∠EAF,若CD=5,CE=3,AE=7,则______.
7.平面直角坐标系内,点在第二象限,则点在第______象限.
8.平面直角坐标系内,到x轴的距离为6、到y轴的距离为9,且在y轴左侧的点的坐标是______.
9.如图,有一种简易的测距工具,为了测量地面上的点M与点O的距离(两点之间有障碍无法直接测量),在点O处立竖杆PO,并将顶端的活动杆PQ对准点M,固定活动杆与竖杆的角度后,转动工具至空旷处,标记活动杆的延长线与地面的交点N,测量点N与点O的距离,该距离即为点M与点O的距离.此种工具用到了全等三角形的判定,其判定理由是______.
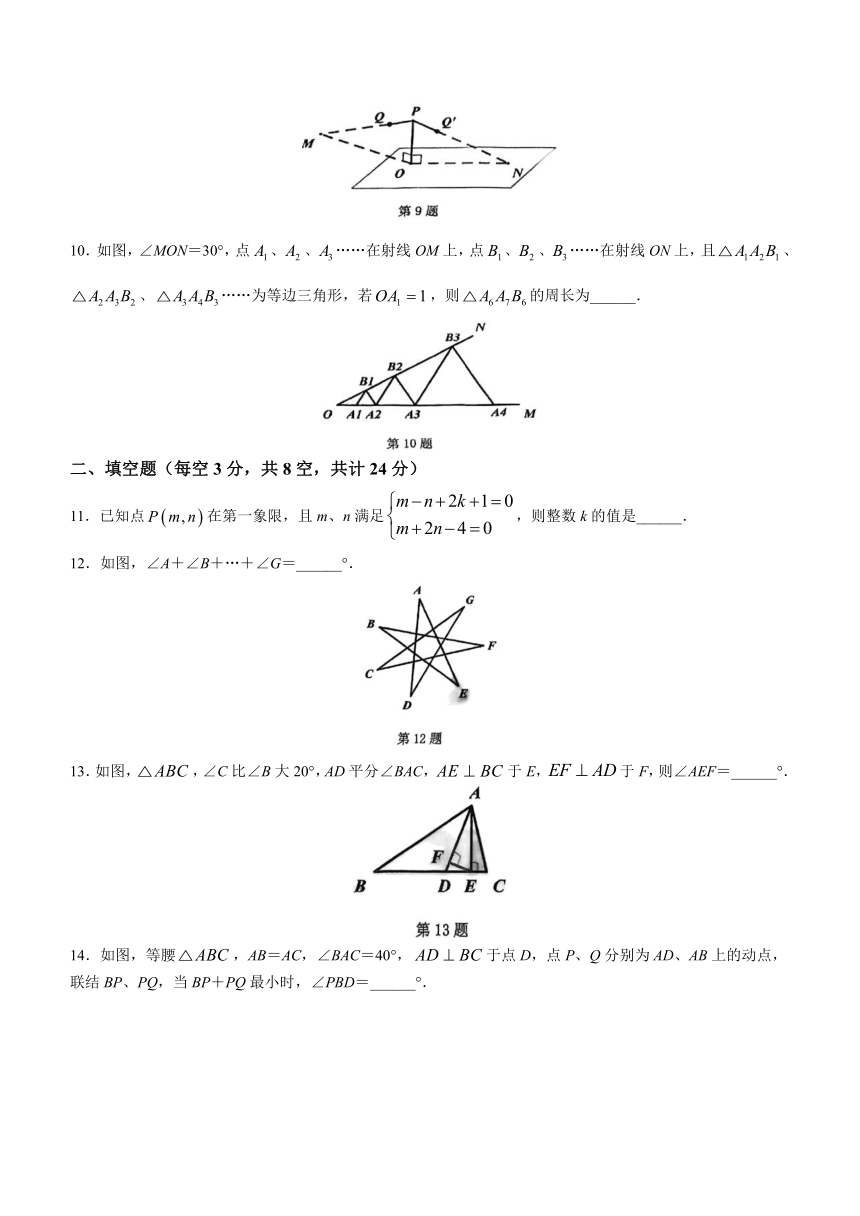
10.如图,∠MON=30°,点、、……在射线OM上,点、、……在射线ON上,且、、……为等边三角形,若,则的周长为______.
二、填空题(每空3分,共8空,共计24分)
11.已知点在第一象限,且m、n满足,则整数k的值是______.
12.如图,∠A+∠B+…+∠G=______°.
13.如图,,∠C比∠B大20°,AD平分∠BAC,于E,于F,则∠AEF=______°.
14.如图,等腰,AB=AC,∠BAC=40°,于点D,点P、Q分别为AD、AB上的动点,联结BP、PQ,当BP+PQ最小时,∠PBD=______°.
15.如图,AB=8,BC=10,CD为射线,∠B=∠C,点P从点B出发沿BC向点C运动,速度为1个单位/秒,点Q从点C出发沿射线CD运动,速度为x个单位/秒;若在某时刻,能与全等,则x=______.
16.如图,在以为直径的半圆O中,作一个矩形OABC,再将矩形OABC绕点C逆时针旋转至矩形,且在半圆上,则旋转角(小于360°)为______°.
17.如图,,延长CB至点D使得BD=BC,过点D作,点F与AB上一点E联结且∠BEF=∠A,若,DF=2,则EF=______.
18.如图,若干个点以箭头方向排列,则第1000个点的坐标为______.
三、选择题(每题3分,共4题,共计12分)
19.下列正确的叙述是( )
A.中心对称图形由两个图形组成
B.圆的对称轴有无数条,就是它的直径
C.正五边形的旋转角只有是72°
D.正六边形既是轴对称图形,也是旋转对称图形,还是中心对称图形
20.下列各图中,已知∠1=∠2,则可以得到的是( )
A. B. C. D.
21.已知两个三角形有一个角及这个角的一条邻边对应相等,若再增加以下某个条件,则不能判断这两个三角形全等的是( )
A.这条边上的高对应相等 B.这条边上的中线对应相等
C.这个角的角平分线对应相等 D.这个角的另一条邻边对应相等
22.已知点P在第一象限,若在x轴上确定点Q使得为等腰三角形,则点Q的坐标有( )种可能
A.3 B.4 C.1或3 D.2或4
四、简答题(每题6分,共2题,共计12分)
23.如图,已知,点A与点关于点O成中心对称,试画出对称中心点O和的对称(此题无需尺规作图,无需写作法,要求精确,需要写结论).
24.如图,已知线段m、n、k,求作使得AB=m,AC=n,AB边上的高为k(此题需要尺规作图,无需写作法,无需作出全等图形,需要写结论).
五、解答题(7分+7分+9分9分,共计32分)
25.已知,∠A<∠B<∠C且度数均为整数,若,求:∠B的度数.(此题7分)
26.在直角坐标平面内,点与点关于x轴对称,将点B绕着原点逆时针旋转90°得点C,求:的面积.(此题7分)
27.(此题需要写出括号内的定理理由,已知、已证、已作、等量代换、等式性质这五条理由不需要写)如图,已知,∠ACB=90°,作且AD=AB,联结CD,过点B作CD的垂线(垂足为点E),与过点A作AC的垂线交于点F,联结CF.
(1)求证:是等腰直角三角形;
(2)联结AE,求证:AE平分∠DEF.(此题9分)
28.(此题不需要写出括号内的定理理由)(1)如图①,四边形ABCD,∠DCB与∠ADC互补,BC=CD,点E、F在线段AB、AD上且BE+DF=EF,若∠A=n°,求:∠ECF的度数;
(2)如图②,若点E、F在线段AB、AD的延长线上,其余条件均不变,求:∠ECF的度数.
(考试时间90分钟,答案写在答卷纸上,不得使用计算器)
一、填空题(每空2分,共10空,共计20分)
1.图形基本运动有______.
2.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3的余角是∠4,若∠4=55°,则∠1=______°.
3.如图,,则∠B、∠C、∠D的关系是______.
4.一个不等边三角形的两边分别为5cm和7cm,第三边的长度为奇数,则满足条件的三角形共有______个.
5.如图,有一个正方形、一个等边三角形、一个等腰直角三角形,则∠1+∠2+∠3=______°.
6.如图,,于F,将AF沿AC翻折至AE,联结EC并延长,在射线EC上取点D使得∠BAD=∠EAF,若CD=5,CE=3,AE=7,则______.
7.平面直角坐标系内,点在第二象限,则点在第______象限.
8.平面直角坐标系内,到x轴的距离为6、到y轴的距离为9,且在y轴左侧的点的坐标是______.
9.如图,有一种简易的测距工具,为了测量地面上的点M与点O的距离(两点之间有障碍无法直接测量),在点O处立竖杆PO,并将顶端的活动杆PQ对准点M,固定活动杆与竖杆的角度后,转动工具至空旷处,标记活动杆的延长线与地面的交点N,测量点N与点O的距离,该距离即为点M与点O的距离.此种工具用到了全等三角形的判定,其判定理由是______.
10.如图,∠MON=30°,点、、……在射线OM上,点、、……在射线ON上,且、、……为等边三角形,若,则的周长为______.
二、填空题(每空3分,共8空,共计24分)
11.已知点在第一象限,且m、n满足,则整数k的值是______.
12.如图,∠A+∠B+…+∠G=______°.
13.如图,,∠C比∠B大20°,AD平分∠BAC,于E,于F,则∠AEF=______°.
14.如图,等腰,AB=AC,∠BAC=40°,于点D,点P、Q分别为AD、AB上的动点,联结BP、PQ,当BP+PQ最小时,∠PBD=______°.
15.如图,AB=8,BC=10,CD为射线,∠B=∠C,点P从点B出发沿BC向点C运动,速度为1个单位/秒,点Q从点C出发沿射线CD运动,速度为x个单位/秒;若在某时刻,能与全等,则x=______.
16.如图,在以为直径的半圆O中,作一个矩形OABC,再将矩形OABC绕点C逆时针旋转至矩形,且在半圆上,则旋转角(小于360°)为______°.
17.如图,,延长CB至点D使得BD=BC,过点D作,点F与AB上一点E联结且∠BEF=∠A,若,DF=2,则EF=______.
18.如图,若干个点以箭头方向排列,则第1000个点的坐标为______.
三、选择题(每题3分,共4题,共计12分)
19.下列正确的叙述是( )
A.中心对称图形由两个图形组成
B.圆的对称轴有无数条,就是它的直径
C.正五边形的旋转角只有是72°
D.正六边形既是轴对称图形,也是旋转对称图形,还是中心对称图形
20.下列各图中,已知∠1=∠2,则可以得到的是( )
A. B. C. D.
21.已知两个三角形有一个角及这个角的一条邻边对应相等,若再增加以下某个条件,则不能判断这两个三角形全等的是( )
A.这条边上的高对应相等 B.这条边上的中线对应相等
C.这个角的角平分线对应相等 D.这个角的另一条邻边对应相等
22.已知点P在第一象限,若在x轴上确定点Q使得为等腰三角形,则点Q的坐标有( )种可能
A.3 B.4 C.1或3 D.2或4
四、简答题(每题6分,共2题,共计12分)
23.如图,已知,点A与点关于点O成中心对称,试画出对称中心点O和的对称(此题无需尺规作图,无需写作法,要求精确,需要写结论).
24.如图,已知线段m、n、k,求作使得AB=m,AC=n,AB边上的高为k(此题需要尺规作图,无需写作法,无需作出全等图形,需要写结论).
五、解答题(7分+7分+9分9分,共计32分)
25.已知,∠A<∠B<∠C且度数均为整数,若,求:∠B的度数.(此题7分)
26.在直角坐标平面内,点与点关于x轴对称,将点B绕着原点逆时针旋转90°得点C,求:的面积.(此题7分)
27.(此题需要写出括号内的定理理由,已知、已证、已作、等量代换、等式性质这五条理由不需要写)如图,已知,∠ACB=90°,作且AD=AB,联结CD,过点B作CD的垂线(垂足为点E),与过点A作AC的垂线交于点F,联结CF.
(1)求证:是等腰直角三角形;
(2)联结AE,求证:AE平分∠DEF.(此题9分)
28.(此题不需要写出括号内的定理理由)(1)如图①,四边形ABCD,∠DCB与∠ADC互补,BC=CD,点E、F在线段AB、AD上且BE+DF=EF,若∠A=n°,求:∠ECF的度数;
(2)如图②,若点E、F在线段AB、AD的延长线上,其余条件均不变,求:∠ECF的度数.
同课章节目录
