北京市海淀区首都师范大学第二附属中学2022_2023学年九年级下学期4月月考数学试题(含答案)
文档属性
| 名称 | 北京市海淀区首都师范大学第二附属中学2022_2023学年九年级下学期4月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1017.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-22 07:56:58 | ||
图片预览



文档简介
首都师大二附中2022—2023学年第二学期练习
初三数学
一、选择题(本题共16分,每小题2分)
第1—8题均有四个选项,符合题意的选项只有一个.
1.2023年4月6日,中国船舶集团有限公司与法国达飞海运集团在北京正式签订合作协议,协议包括建造2型16艘大型集装箱船,金额达21000000000多元人民币,创下了中国造船业一次性签约集装箱船最大金额的新纪录。请将21000000000用科学记数法表示( )
A. B. C. D.
2.如图的几何体是由一些小正方体组合而成的,则这个几何体的左视图是( )
A.B.C.D.
3.如图,已知,,平分,则的度数是( )
A. B. C. D.
4.图中的图形为轴对称图形,该图形的对称轴的条数为( )
A.1 B.2 C.4 D.8
5.若正多边形的一个外角是,则该正多边形的内角和为( )
A. B. C. D.
6.“天宫课堂”第二课3月23日在中国空间站开讲,包括六个项目:太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节.若随机选取一个项目写观后感,则恰好选到“实验”项目的概率是( )
A. B. C. D.
7.实数,在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
8.如图1,矩形的一条边长为,周长的一半为.定义为这个矩形的坐标.如图2,在平面直角坐标系中,直线,将第一象限划分成4个区域.已知矩形1的坐标的对应点落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中.则下面叙述中正确的是( )
A.点的横坐标有可能大于3
B.矩形1是正方形时,点位于区域②
C.当点沿双曲线向上移动时,矩形1的面积减小
D.当点位于区域①时,矩形1可能和矩形2全等
二、填空题(本题共16分,每小题2分)
9.若式子在实数范围内有意义,则的取值范围是______.
10.分解因式:______.
11.方程的解为______.
12.如图,,是的弦,,是的切线,若,则______°.
13.在平面直角坐标系中,若点,在反比例函数的图象上,则______填“>”“=”或“<”)
14.如图,在矩形中,若,,,则的长为______.
15.为了丰富同学们的课余生活,某年级买了3个篮球和2个足球,共花费了474元,其中篮球的单价比足球的单价多8元,求篮球和足球的单价,如果设篮球的单价为元,足球的单价为元,依题意可列方程组为______.
16.如图①,在中,,点从点出发沿以的速度运动到点,过点作千点,图②是点运动时,线段的长度随运动时间的变化关系的图象,当时,的值可能为______.
三、解答题(共68分,第17—20题,每题5分,第21题6分,第22题5分,第23—24题,每题6分,第25题5分,第26题6分,第27—28题,每题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:.
18.解不等式组:
19.已知,求代数式的值.
20.关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求的取值范围.
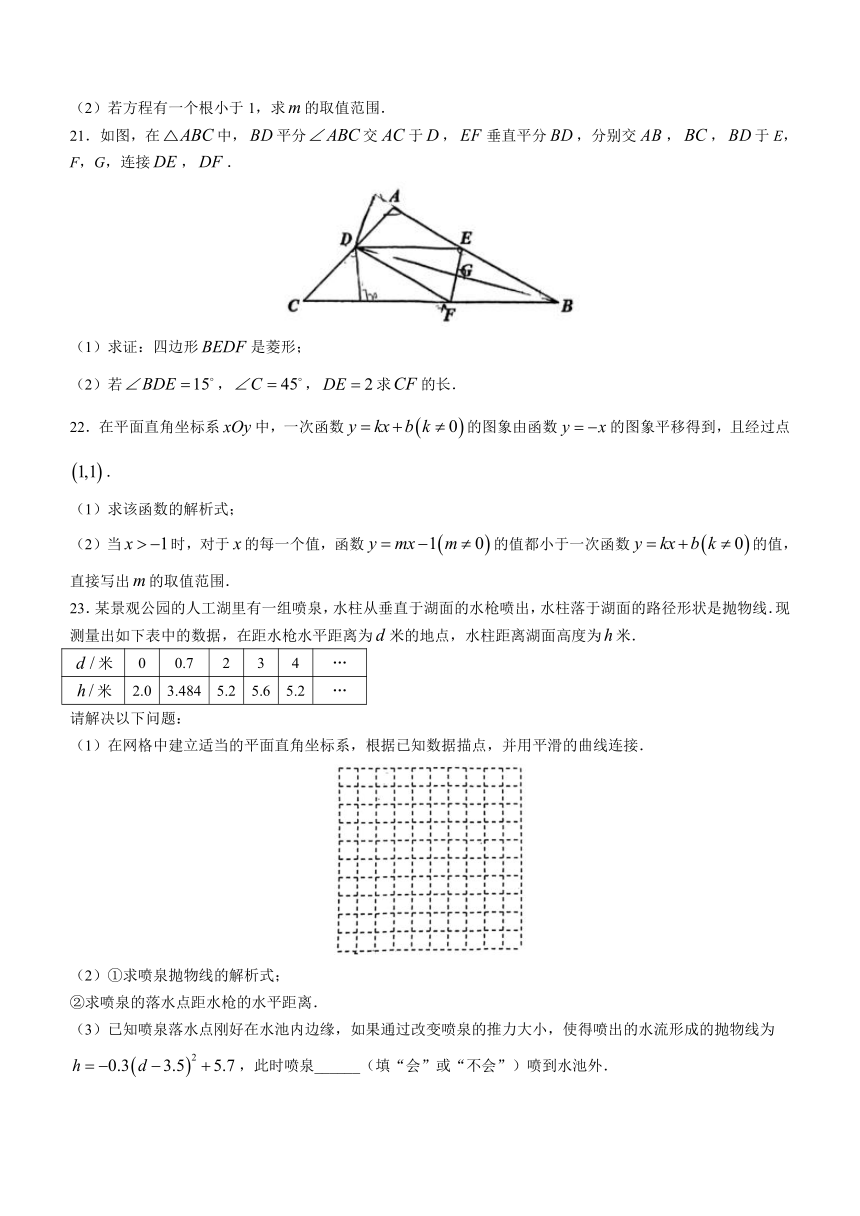
21.如图,在中,平分交于,垂直平分,分别交,,于E,F,G,连接,.
(1)求证:四边形是菱形;
(2)若,,求的长.
22.在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点.
(1)求该函数的解析式;
(2)当时,对于的每一个值,函数的值都小于一次函数的值,直接写出的取值范围.
23.某景观公园的人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下表中的数据,在距水枪水平距离为米的地点,水柱距离湖面高度为米.
米 0 0.7 2 3 4 …
米 2.0 3.484 5.2 5.6 5.2 …
请解决以下问题:
(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接.
(2)①求喷泉抛物线的解析式;
②求喷泉的落水点距水枪的水平距离.
(3)已知喷泉落水点刚好在水池内边缘,如果通过改变喷泉的推力大小,使得喷出的水流形成的抛物线为,此时喷泉______(填“会”或“不会”)喷到水池外.
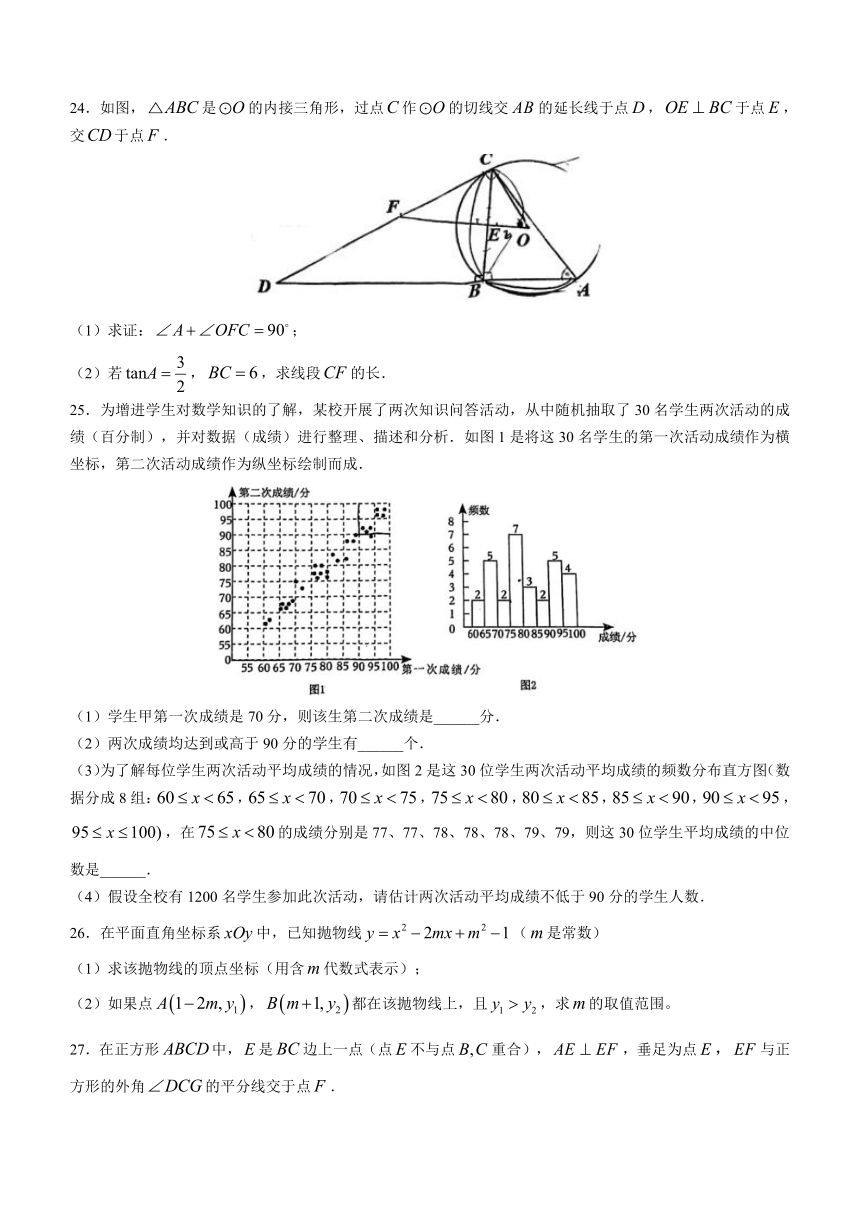
24.如图,是的内接三角形,过点作的切线交的延长线于点,于点,交于点.
(1)求证:;
(2)若,,求线段的长.
25.为增进学生对数学知识的了解,某校开展了两次知识问答活动,从中随机抽取了30名学生两次活动的成绩(百分制),并对数据(成绩)进行整理、描述和分析.如图1是将这30名学生的第一次活动成绩作为横坐标,第二次活动成绩作为纵坐标绘制而成.
(1)学生甲第一次成绩是70分,则该生第二次成绩是______分.
(2)两次成绩均达到或高于90分的学生有______个.
(3)为了解每位学生两次活动平均成绩的情况,如图2是这30位学生两次活动平均成绩的频数分布直方图(数据分成8组:,,,,,,,,在的成绩分别是77、77、78、78、78、79、79,则这30位学生平均成绩的中位数是______.
(4)假设全校有1200名学生参加此次活动,请估计两次活动平均成绩不低于90分的学生人数.
26.在平面直角坐标系中,已知抛物线(是常数)
(1)求该抛物线的顶点坐标(用含代数式表示);
(2)如果点,都在该抛物线上,且,求的取值范围。
27.在正方形中,是边上一点(点不与点重合),,垂足为点,与正方形的外角的平分线交于点.
(1)如图1,若点是的中点,猜想与的数量关系是______.
证明此猜想时,可取的中点,连接.根据此图形易证.
则判断的依据是______.
(2)点在边上运动.
①如图2,(1)中的猜想是否仍然成立?请说明理由.
②如图3,连接,,若正方形的边长为2,直接写出的周长的取值范围.
28.在平面直角坐标系中,的半径为2,对于平面上的任一点,给出如下定义:在射线上存在点,使得,则称点是点关于的“映象点”.
(1)点关于的“映象点”是______,点关于的“映象点”是______;
(2)如图1,过点垂直于轴的直线交圆于点,,当点在线段上运动时,记点是点关于圆的“映象点”,直接写出点的横坐标的取值范围;
(3)如图2,过点垂直于轴的直线交圆于点,当点在线段上运动时,记点关于圆的“映象点”的轨迹为,当时,直接写出的长度的取值范围.
首都师大二附中2022—2023学年第二学期练习
初三数学答案
题号 1 2 3 4 5 6 7 8
答案 B B D C C A B D
9. 10. 11. 12.60 13.< 14.2
15. 16.6(答案不唯一,均可)
17.原式.
18.解:,解不等式①得:;解不等式②得:,
∴不等式组的解集是.
19.解:∵,∴,
原式,
当时,原式.
20.(1)证明:∵,,,
∴,
∴此方程总有两个实数根.
(2)解:,∴
∴,.
∵此方程有一个根小于1.∴,∴.
21.证明:(1)∵平分,∴
∵垂直平分,∴,,
∵,,
∴,,
∴,,∴四边形是平行四边形,且,
∴四边形是菱形;
(2)过点作于点,
∵四边形是菱形,
∴,
∴,
∴,且,
∴,,
∵,,
∴,
∴,∴.
22.解:(1)∵一次函数的图象由函数的图象平移得到,∴,
又∵一次函数的图象过点,
∴,∴,
∴这个一次函数的表达式为;
(2)
23.解:(1)如图:
(2)①由图象得,顶点,设,
把代入可得,∴;
②当时,,
解得或(舍去),
答:喷泉的落水点距水枪的水平距离约为米,
故答案为:;
(3)会;
24.(1)证明:如图,连接,
∵是的切线,∴,∴,∴,
∵,∴,∴;
(2)解:∵,∴,
∵,∴,
∴,∴,
∵,∴,
∴,∴,∴,
∴,∴.
25.解:(1)由图1得:该生第二次成绩是75分,故答案为:75;
(2)横纵坐标都大于等于90的点有7个,故答案为:7;
(3)这30位学生平均成绩的中位数是:79,故答案为:79;
(4)(人),
答:估计两次活动平均成绩不低于90分的学生有360人.
26.解:(1),顶点
(2)或
27.解:(1),;
(2)①成立,理由如下:
如图2,在上取一点,使,连接,则,
由(1)得:,
∵,,∴是等腰直角三角形,
∴,∴,∴,
在和中,,∴,∴
②如图3,过作交于点,连接、,
的周长的取值范围是.
28.(1);
(2)
(3)
初三数学
一、选择题(本题共16分,每小题2分)
第1—8题均有四个选项,符合题意的选项只有一个.
1.2023年4月6日,中国船舶集团有限公司与法国达飞海运集团在北京正式签订合作协议,协议包括建造2型16艘大型集装箱船,金额达21000000000多元人民币,创下了中国造船业一次性签约集装箱船最大金额的新纪录。请将21000000000用科学记数法表示( )
A. B. C. D.
2.如图的几何体是由一些小正方体组合而成的,则这个几何体的左视图是( )
A.B.C.D.
3.如图,已知,,平分,则的度数是( )
A. B. C. D.
4.图中的图形为轴对称图形,该图形的对称轴的条数为( )
A.1 B.2 C.4 D.8
5.若正多边形的一个外角是,则该正多边形的内角和为( )
A. B. C. D.
6.“天宫课堂”第二课3月23日在中国空间站开讲,包括六个项目:太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节.若随机选取一个项目写观后感,则恰好选到“实验”项目的概率是( )
A. B. C. D.
7.实数,在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
8.如图1,矩形的一条边长为,周长的一半为.定义为这个矩形的坐标.如图2,在平面直角坐标系中,直线,将第一象限划分成4个区域.已知矩形1的坐标的对应点落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中.则下面叙述中正确的是( )
A.点的横坐标有可能大于3
B.矩形1是正方形时,点位于区域②
C.当点沿双曲线向上移动时,矩形1的面积减小
D.当点位于区域①时,矩形1可能和矩形2全等
二、填空题(本题共16分,每小题2分)
9.若式子在实数范围内有意义,则的取值范围是______.
10.分解因式:______.
11.方程的解为______.
12.如图,,是的弦,,是的切线,若,则______°.
13.在平面直角坐标系中,若点,在反比例函数的图象上,则______填“>”“=”或“<”)
14.如图,在矩形中,若,,,则的长为______.
15.为了丰富同学们的课余生活,某年级买了3个篮球和2个足球,共花费了474元,其中篮球的单价比足球的单价多8元,求篮球和足球的单价,如果设篮球的单价为元,足球的单价为元,依题意可列方程组为______.
16.如图①,在中,,点从点出发沿以的速度运动到点,过点作千点,图②是点运动时,线段的长度随运动时间的变化关系的图象,当时,的值可能为______.
三、解答题(共68分,第17—20题,每题5分,第21题6分,第22题5分,第23—24题,每题6分,第25题5分,第26题6分,第27—28题,每题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:.
18.解不等式组:
19.已知,求代数式的值.
20.关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求的取值范围.
21.如图,在中,平分交于,垂直平分,分别交,,于E,F,G,连接,.
(1)求证:四边形是菱形;
(2)若,,求的长.
22.在平面直角坐标系中,一次函数的图象由函数的图象平移得到,且经过点.
(1)求该函数的解析式;
(2)当时,对于的每一个值,函数的值都小于一次函数的值,直接写出的取值范围.
23.某景观公园的人工湖里有一组喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下表中的数据,在距水枪水平距离为米的地点,水柱距离湖面高度为米.
米 0 0.7 2 3 4 …
米 2.0 3.484 5.2 5.6 5.2 …
请解决以下问题:
(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接.
(2)①求喷泉抛物线的解析式;
②求喷泉的落水点距水枪的水平距离.
(3)已知喷泉落水点刚好在水池内边缘,如果通过改变喷泉的推力大小,使得喷出的水流形成的抛物线为,此时喷泉______(填“会”或“不会”)喷到水池外.
24.如图,是的内接三角形,过点作的切线交的延长线于点,于点,交于点.
(1)求证:;
(2)若,,求线段的长.
25.为增进学生对数学知识的了解,某校开展了两次知识问答活动,从中随机抽取了30名学生两次活动的成绩(百分制),并对数据(成绩)进行整理、描述和分析.如图1是将这30名学生的第一次活动成绩作为横坐标,第二次活动成绩作为纵坐标绘制而成.
(1)学生甲第一次成绩是70分,则该生第二次成绩是______分.
(2)两次成绩均达到或高于90分的学生有______个.
(3)为了解每位学生两次活动平均成绩的情况,如图2是这30位学生两次活动平均成绩的频数分布直方图(数据分成8组:,,,,,,,,在的成绩分别是77、77、78、78、78、79、79,则这30位学生平均成绩的中位数是______.
(4)假设全校有1200名学生参加此次活动,请估计两次活动平均成绩不低于90分的学生人数.
26.在平面直角坐标系中,已知抛物线(是常数)
(1)求该抛物线的顶点坐标(用含代数式表示);
(2)如果点,都在该抛物线上,且,求的取值范围。
27.在正方形中,是边上一点(点不与点重合),,垂足为点,与正方形的外角的平分线交于点.
(1)如图1,若点是的中点,猜想与的数量关系是______.
证明此猜想时,可取的中点,连接.根据此图形易证.
则判断的依据是______.
(2)点在边上运动.
①如图2,(1)中的猜想是否仍然成立?请说明理由.
②如图3,连接,,若正方形的边长为2,直接写出的周长的取值范围.
28.在平面直角坐标系中,的半径为2,对于平面上的任一点,给出如下定义:在射线上存在点,使得,则称点是点关于的“映象点”.
(1)点关于的“映象点”是______,点关于的“映象点”是______;
(2)如图1,过点垂直于轴的直线交圆于点,,当点在线段上运动时,记点是点关于圆的“映象点”,直接写出点的横坐标的取值范围;
(3)如图2,过点垂直于轴的直线交圆于点,当点在线段上运动时,记点关于圆的“映象点”的轨迹为,当时,直接写出的长度的取值范围.
首都师大二附中2022—2023学年第二学期练习
初三数学答案
题号 1 2 3 4 5 6 7 8
答案 B B D C C A B D
9. 10. 11. 12.60 13.< 14.2
15. 16.6(答案不唯一,均可)
17.原式.
18.解:,解不等式①得:;解不等式②得:,
∴不等式组的解集是.
19.解:∵,∴,
原式,
当时,原式.
20.(1)证明:∵,,,
∴,
∴此方程总有两个实数根.
(2)解:,∴
∴,.
∵此方程有一个根小于1.∴,∴.
21.证明:(1)∵平分,∴
∵垂直平分,∴,,
∵,,
∴,,
∴,,∴四边形是平行四边形,且,
∴四边形是菱形;
(2)过点作于点,
∵四边形是菱形,
∴,
∴,
∴,且,
∴,,
∵,,
∴,
∴,∴.
22.解:(1)∵一次函数的图象由函数的图象平移得到,∴,
又∵一次函数的图象过点,
∴,∴,
∴这个一次函数的表达式为;
(2)
23.解:(1)如图:
(2)①由图象得,顶点,设,
把代入可得,∴;
②当时,,
解得或(舍去),
答:喷泉的落水点距水枪的水平距离约为米,
故答案为:;
(3)会;
24.(1)证明:如图,连接,
∵是的切线,∴,∴,∴,
∵,∴,∴;
(2)解:∵,∴,
∵,∴,
∴,∴,
∵,∴,
∴,∴,∴,
∴,∴.
25.解:(1)由图1得:该生第二次成绩是75分,故答案为:75;
(2)横纵坐标都大于等于90的点有7个,故答案为:7;
(3)这30位学生平均成绩的中位数是:79,故答案为:79;
(4)(人),
答:估计两次活动平均成绩不低于90分的学生有360人.
26.解:(1),顶点
(2)或
27.解:(1),;
(2)①成立,理由如下:
如图2,在上取一点,使,连接,则,
由(1)得:,
∵,,∴是等腰直角三角形,
∴,∴,∴,
在和中,,∴,∴
②如图3,过作交于点,连接、,
的周长的取值范围是.
28.(1);
(2)
(3)
同课章节目录
