勾股定理第1课时
图片预览




文档简介
课件20张PPT。复习提问 1、任意三角形三边满足怎样的关系?2、对于等腰三角形,三边之间存在怎样的特殊关系?等边三角形呢?3、对于直角三角形,三边之间存在怎样的特殊关系?17、1勾股定理学习目标:
1.探索直角三角形三边关系。
2.了解勾股定理的证明方法
3.能用勾股定理进行简单计算 学法指导:
认真看课本P22_24页练习前
1、完成22页的思考题及24页的探究。
2、猜想直角三角三边有怎样的关系。
3、理解赵爽是如何用面积法证明勾股定理的。
4、想一想:勾股定理的适用条件是什么?
5分钟后检测同学们看书情况
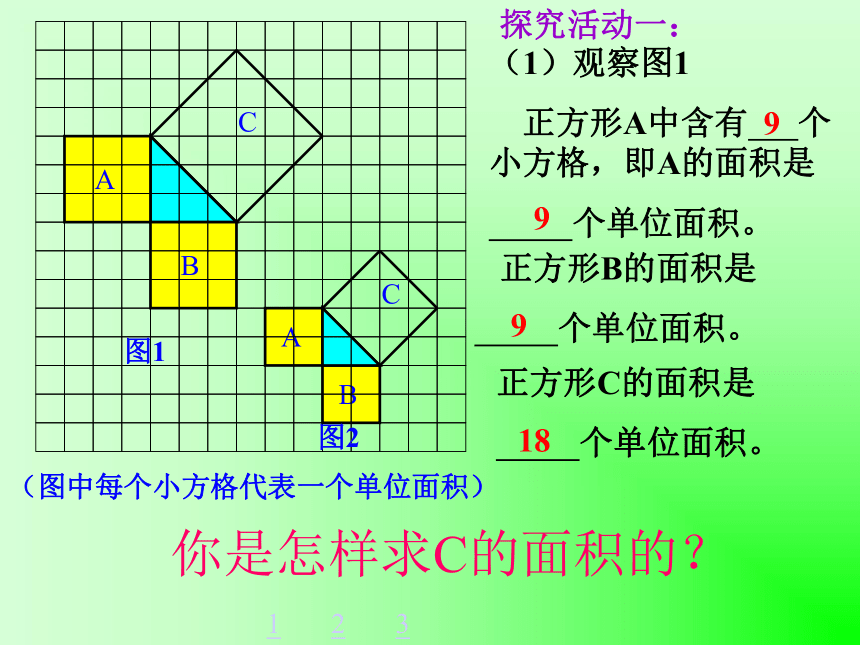
(1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
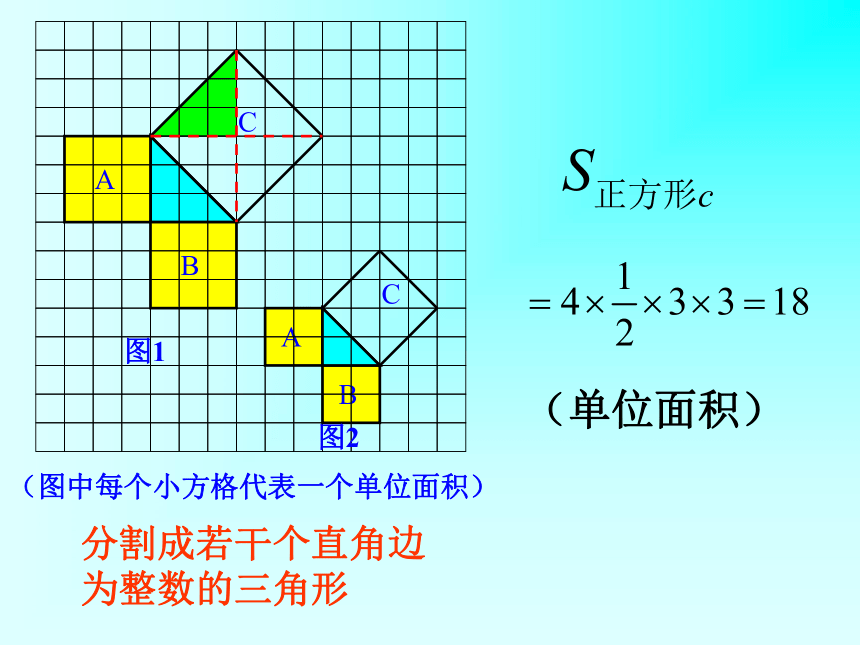
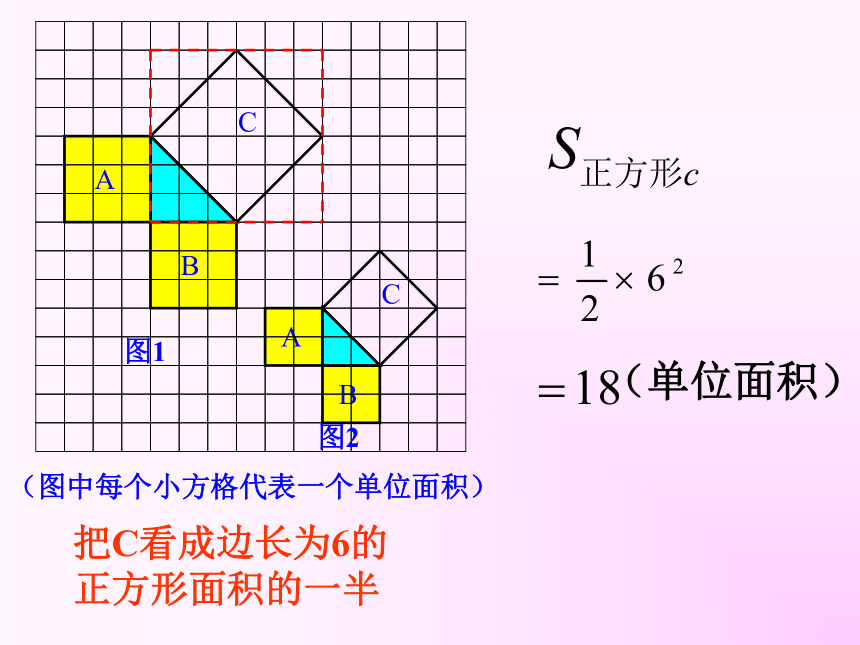
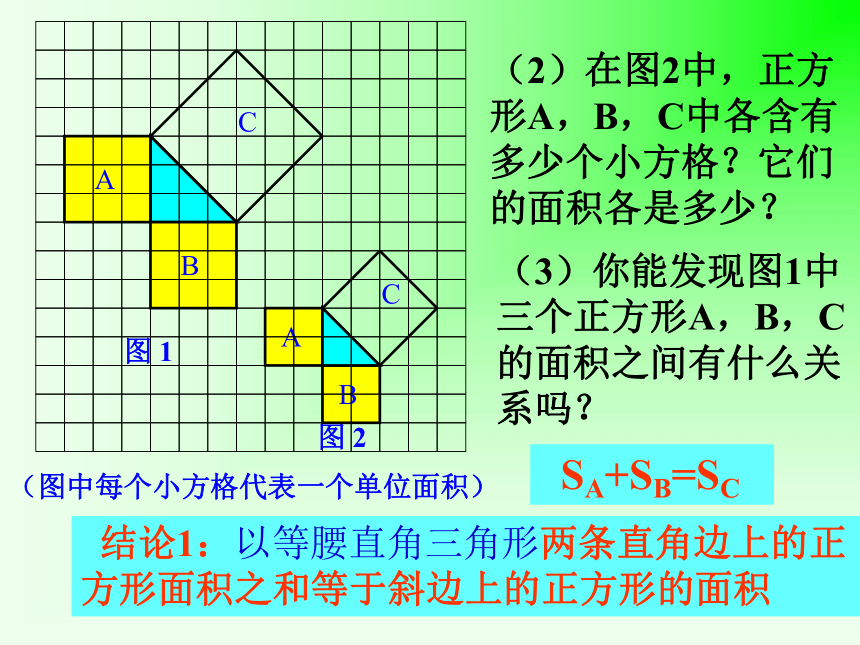
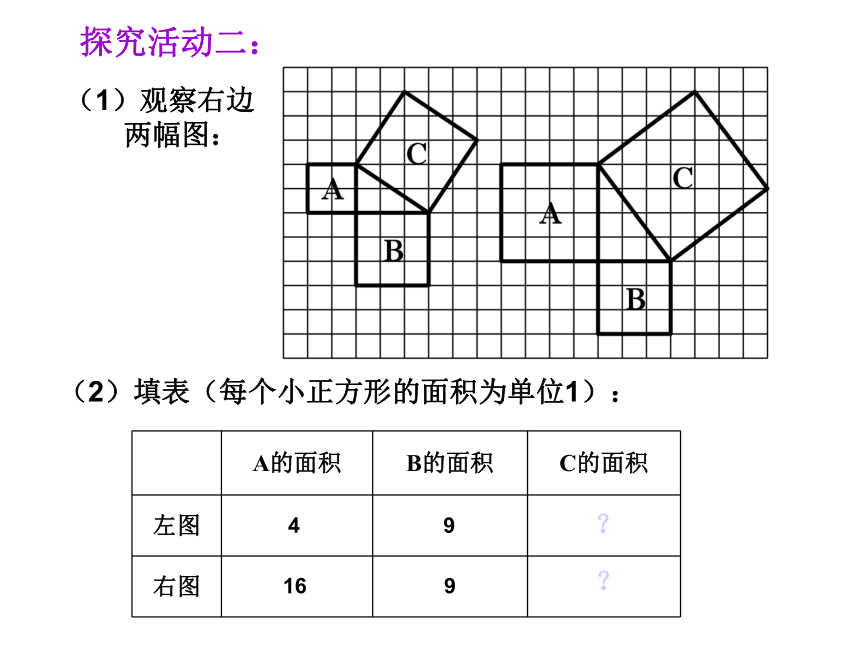
个单位面积。99918123探究活动一:你是怎样求C的面积的?分割成若干个直角边为整数的三角形(单位面积)(单位面积)把C看成边长为6的正方形面积的一半(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 结论1:以等腰直角三角形两条直角边上的正方形面积之和等于斜边上的正方形的面积探究活动二:(1)观察右边
两幅图: (2)填表(每个小正方形的面积为单位1):4 916 9??(3)你是怎样得到正方形C的面积的?与同伴交流. (4)分析填表数据,你发现了什么? 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.议一议: (1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗? (2)你能发现直角三角形三边长度之间存在什么
关系吗? 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。表示为:Rt△ABC中,∠C=90° 则勾2+股2=弦2用赵爽弦图证明勾股定理=结论:S1+S2+S3+S4=S5+S6 =S7=10
S5=s1+s2=4S6=s3+s4=61、2、求出下列直角三角形中未知的边.245°①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?8171两个条件斜边方法小结:可用勾股定理建立方程.√3?√2√2CABACB说说这节课你有什么收获?收获与反思想一想我们这一节课有哪些收获? 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a21.必做题:习题17.1 第1, 7,8题。
2.选做题:课本 “阅读与思考”,了解
勾股定理的多种证法。布置作业:
1.探索直角三角形三边关系。
2.了解勾股定理的证明方法
3.能用勾股定理进行简单计算 学法指导:
认真看课本P22_24页练习前
1、完成22页的思考题及24页的探究。
2、猜想直角三角三边有怎样的关系。
3、理解赵爽是如何用面积法证明勾股定理的。
4、想一想:勾股定理的适用条件是什么?
5分钟后检测同学们看书情况
(1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918123探究活动一:你是怎样求C的面积的?分割成若干个直角边为整数的三角形(单位面积)(单位面积)把C看成边长为6的正方形面积的一半(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 结论1:以等腰直角三角形两条直角边上的正方形面积之和等于斜边上的正方形的面积探究活动二:(1)观察右边
两幅图: (2)填表(每个小正方形的面积为单位1):4 916 9??(3)你是怎样得到正方形C的面积的?与同伴交流. (4)分析填表数据,你发现了什么? 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.议一议: (1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗? (2)你能发现直角三角形三边长度之间存在什么
关系吗? 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。表示为:Rt△ABC中,∠C=90° 则勾2+股2=弦2用赵爽弦图证明勾股定理=结论:S1+S2+S3+S4=S5+S6 =S7=10
S5=s1+s2=4S6=s3+s4=61、2、求出下列直角三角形中未知的边.245°①在解决上述问题时,每个直角三角形需知道几个条件?②直角三角形哪条边最长?8171两个条件斜边方法小结:可用勾股定理建立方程.√3?√2√2CABACB说说这节课你有什么收获?收获与反思想一想我们这一节课有哪些收获? 勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a21.必做题:习题17.1 第1, 7,8题。
2.选做题:课本 “阅读与思考”,了解
勾股定理的多种证法。布置作业:
