1.3.2 直线的极坐标方程 课件(共16张PPT)
文档属性
| 名称 | 1.3.2 直线的极坐标方程 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 707.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 11:23:37 | ||
图片预览




文档简介
(共16张PPT)
刘俊斌模板之5
直线的极坐标方程
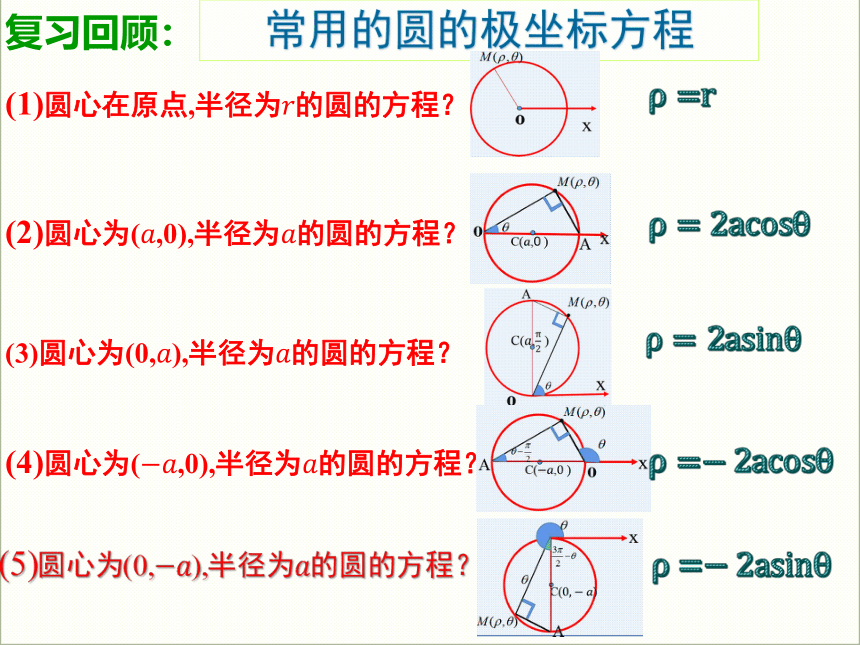
常用的圆的极坐标方程
复习回顾:
(1)圆心在原点,半径为的圆的方程?
r
(2)圆心为(,0),半径为的圆的方程?
cos
(3)圆心为(0,),半径为的圆的方程?
sin
(4)圆心为(,0),半径为的圆的方程?
cos
(5)圆心为(0,),半径为的圆的方程?
sin
在极坐标系中求曲线方程的基本步骤:
①根据题意建立适当的极坐标系画出示意图;
②设P(ρ,θ )为所求曲线上的任意一点;
③连结OP,寻找OP满足的限制条件;
④代入点坐标,列出关于ρ、θ 的方程;
⑤对方程进行化简:
⑥检验并确定所得方程即为所求。
在极坐标系中求过极点的圆的方程的方法:
(1)利用直径,构造直角三角形。
(2)化为直角坐标,求出方程后,在化为极坐标方程。(转化)
复习回顾:
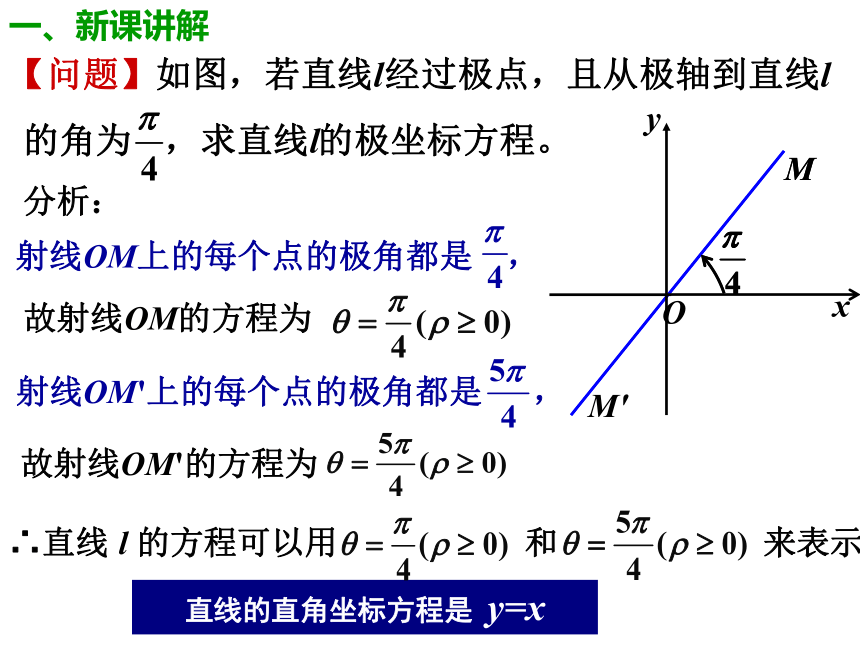
一、新课讲解
O
x
M
M'
M
y
直线的直角坐标方程是 y=x
射线OM上的每个点的极角都是 ,
故射线OM的方程为
射线OM'上的每个点的极角都是 ,
故射线OM'的方程为
分析:
∴直线 l 的方程可以用 和 来表示
一、新课讲解
O
x
M
M'
M
分析:
∴直线 l 的方程可以用
和 来表示
注意:若允许 ρ 取负值(即ρ ∈ R),
一般情况下,题目如果没有专门说明,则 ρ≥0
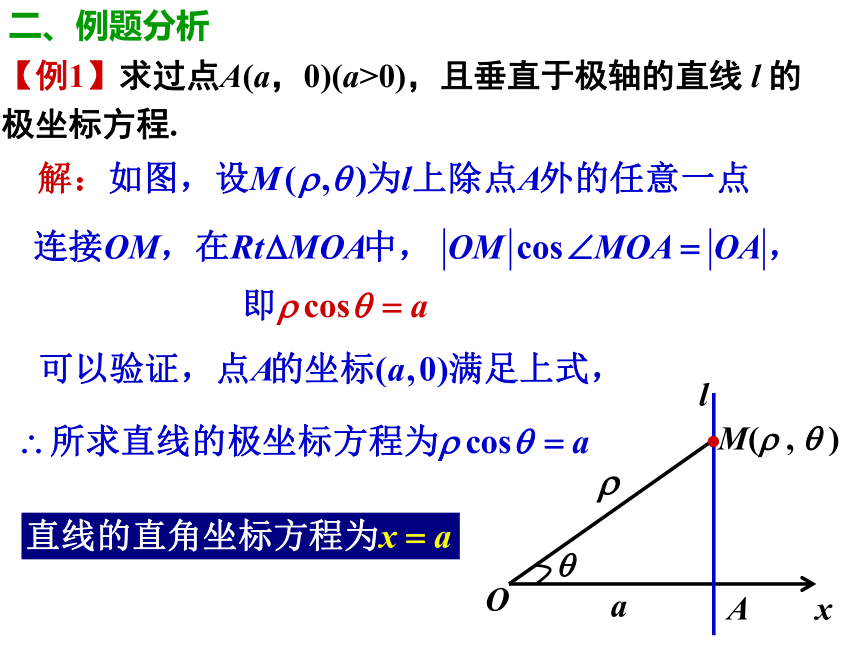
【例1】求过点A(a,0)(a>0),且垂直于极轴的直线 l 的极坐标方程.
l
O
A
x
a
M(r , q )
二、例题分析
三、课堂随练
求直线的极坐标方程步骤
1、据题意画出草图;
2、设点 是直线上任意一点;
3、连接MO;
4、根据几何条件建立关于 的方程,并化简;
5、检验并确认所得的方程即为所求。
课堂随练
O
B
A
M(r,q )
x
N
3:设点A的极坐标为 ,直线 过点
解:如图,建立极坐标系,设点
为直线 上异于A点的任意一点,连接OM,
在 中,由正弦定理 得
显然A点也满足上方程
A且与极轴所成的角为 ,求直线 的极坐标方程。
化简得
﹚
O
M
x
A
﹚
x
O
A
l
M(r, q )
二、例题分析
二、例题分析
x
O
A
l
M(r, q )
直线的几种极坐标方程
1、过极点的直线
2、过定点A(a,0)垂直于极轴
4、过某个定点P ,且与极轴成的角度α
3、过定点A(a, )平行于极轴
o
x
﹚
A
M
M
o
x
﹚
A
﹚
o
o
x
M
P
﹚
﹚
A
sin =a
A、两条相交的直线
B、两条射线
C、一条直线
D、一条射线
三、课后练习
( )
B
( )
B
刘俊斌模板之5
直线的极坐标方程
常用的圆的极坐标方程
复习回顾:
(1)圆心在原点,半径为的圆的方程?
r
(2)圆心为(,0),半径为的圆的方程?
cos
(3)圆心为(0,),半径为的圆的方程?
sin
(4)圆心为(,0),半径为的圆的方程?
cos
(5)圆心为(0,),半径为的圆的方程?
sin
在极坐标系中求曲线方程的基本步骤:
①根据题意建立适当的极坐标系画出示意图;
②设P(ρ,θ )为所求曲线上的任意一点;
③连结OP,寻找OP满足的限制条件;
④代入点坐标,列出关于ρ、θ 的方程;
⑤对方程进行化简:
⑥检验并确定所得方程即为所求。
在极坐标系中求过极点的圆的方程的方法:
(1)利用直径,构造直角三角形。
(2)化为直角坐标,求出方程后,在化为极坐标方程。(转化)
复习回顾:
一、新课讲解
O
x
M
M'
M
y
直线的直角坐标方程是 y=x
射线OM上的每个点的极角都是 ,
故射线OM的方程为
射线OM'上的每个点的极角都是 ,
故射线OM'的方程为
分析:
∴直线 l 的方程可以用 和 来表示
一、新课讲解
O
x
M
M'
M
分析:
∴直线 l 的方程可以用
和 来表示
注意:若允许 ρ 取负值(即ρ ∈ R),
一般情况下,题目如果没有专门说明,则 ρ≥0
【例1】求过点A(a,0)(a>0),且垂直于极轴的直线 l 的极坐标方程.
l
O
A
x
a
M(r , q )
二、例题分析
三、课堂随练
求直线的极坐标方程步骤
1、据题意画出草图;
2、设点 是直线上任意一点;
3、连接MO;
4、根据几何条件建立关于 的方程,并化简;
5、检验并确认所得的方程即为所求。
课堂随练
O
B
A
M(r,q )
x
N
3:设点A的极坐标为 ,直线 过点
解:如图,建立极坐标系,设点
为直线 上异于A点的任意一点,连接OM,
在 中,由正弦定理 得
显然A点也满足上方程
A且与极轴所成的角为 ,求直线 的极坐标方程。
化简得
﹚
O
M
x
A
﹚
x
O
A
l
M(r, q )
二、例题分析
二、例题分析
x
O
A
l
M(r, q )
直线的几种极坐标方程
1、过极点的直线
2、过定点A(a,0)垂直于极轴
4、过某个定点P ,且与极轴成的角度α
3、过定点A(a, )平行于极轴
o
x
﹚
A
M
M
o
x
﹚
A
﹚
o
o
x
M
P
﹚
﹚
A
sin =a
A、两条相交的直线
B、两条射线
C、一条直线
D、一条射线
三、课后练习
( )
B
( )
B
