2.1.2 有理数 课件(共27张PPT)
文档属性
| 名称 | 2.1.2 有理数 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 07:06:27 | ||
图片预览








文档简介
(共27张PPT)
*
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
*
上节课我们学习了什么内容
1正数与负数
2零既不是正数也不是负数
3正数和负数是表示具有相反意义的量
4零表示的意义
5实际生活中,通常用正负数表示允许误差
*
1 明白有理数的概念,知道有理数的分类,体会分类思想的应用。
2 知道集合的概念,会将有理数按要求分类。
3 在学习过程中,积累学习数学的方法,激发学习数学的热情。
学习目标
学习重点
有理数的分类
*
练一练 学一学
依据生活小常识回答问题
1.小明家养了一群小鸡,没事的时候小明在家数小鸡,所得的数是属于什么数?
正数
2.在你的刻度尺上可以读出哪几类有理数?
正数 0 分数
3.蔬菜大棚里的温度计上,能读出哪几类有理数?
正数 零 负数
*
12.96,
182.5,
110,
12.91,
1.1,
-52
0,
+75,
122.5,
+10.
-7.5,
18,
305,
1.在上面各数中,哪些是在小学里学过的数 它们可以分为哪几类
2.在上面的数中,哪些数不是小学所学的数 .
3.计算下列各分数的值,说明所有分数都可以化作什么数
探究1
4.由前面的结论,小学里学的数可以分为哪几类
5.引入负数后,整数除了小学学的整数外,还包含其它的整数吗?
分数除了小学学的分数外,还包含其它的分数吗?
分数均可化为有限小数和无限循环小数.
*
到目前为止,我们学过的数可以分为以下几类?
正整数:如1,2,3,…;
零:0;
负整数:如-1,-2,-3,…;
正分数:如
负分数:如
1、正整数、0和负整数统称为整数;
2、正分数、负分数统称为分数;
3、整数和分数统称为有理数;
*
正整数 零 负整数统称整数
正分数和负分数统称分数
整数和分数统称有理数
*
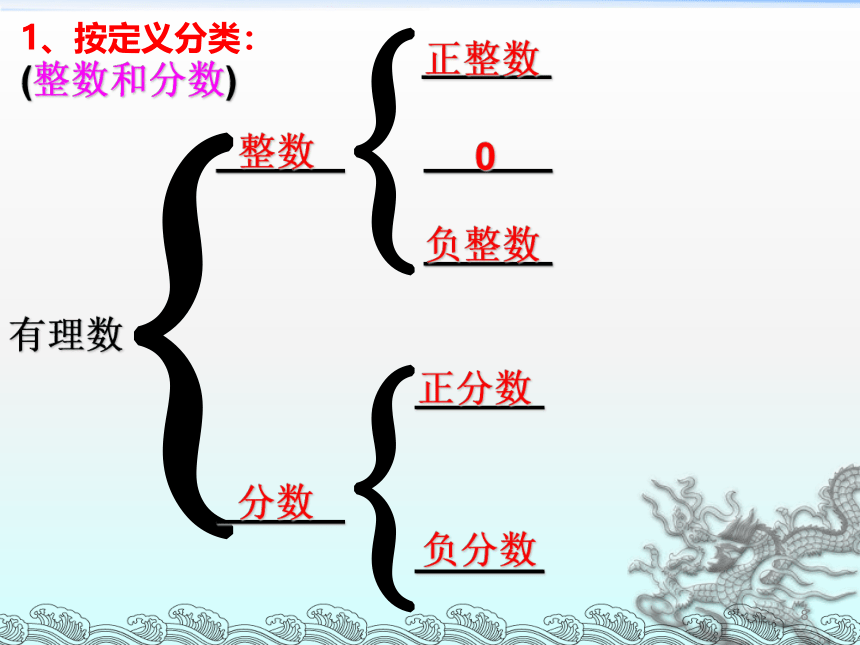
(整数和分数)
有理数
______
______
______
______
______
______
______
整数
分数
正整数
0
负整数
正分数
负分数
1、按定义分类:
*
有理数分类的几点注意:
1,如 能约分成整数的数_____(填“能”或“不能”)算做分数;
不能
2,无限不循环小数不是有理数;
3,整数中除了正整数和负整数,还有_____.
0
有理数还有其他的分类方法吗?
*
有理数
______
______
______
______
______
______
______
正数
0
负数
正整数
正分数
负整数
负分数
2、按性质分类:
注意:①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
(正数、0和负数)
1.在左面的有理数中,
正整数有:__________;
负分数有:_____________________________;整数有:_______________________________;分数有:_______________________________.
探究有理数的分类(二)
小组讨论,合作完成讨论题,集中交流,形成正确分类方法,学生画出分类示意图,同桌合作画出与分类对应的有理数树.
2.丹丹在做第1题时,发现了新的分类方法,她认为:带“+”的数分为一类,带“-”的数分为一类,数的前面没有符号的作为一类.你认为她的分类方法对吗 若不对,你发现什么新的分类方法吗
探究2
-
新知讲解
数集
定义:把一些数放在一起,就组成一类数的集合,简称数集。
所有有理数组成的数集叫做有理数集;
所有整数组成的数集叫做整数集;
所有正数组成的数集叫做正数集;
所有负数组成的数集叫做负数集;
若按集合分类,则每个集合最后要加上“…”。
注意:
一类数的集合必须是符合条件的所有数,不能遗漏。
若一类数的集合有无数个数,则表示这个数的集合时,除写上题中给定的有限个数之外,必须加上省略号。
*
例1:把下列各数填在相应的集合中:
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ };
注意:1.像 这种可以先化简成整数的数是整数不是分数;
2.所有小数归为分数.
把下列各数填入它所属于的集合的圈内:
15, , , , ,
-0.1, , , -123,2.33.
正分数集合 负整数集合
正整数集合 负分数集合
以上四个集合能组成有理数集合吗?
随堂练习
-
*
例2,下列说法正确的是 ( )
A.非负有理数就是正有理数
B. 0仅表示没有,是有理数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数
D
练习:判断正误
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
*
例3 :填空
(1)既是分数又是负数的数是_______;
(2)非负数包括________和_______;
(3)非正数包括________和_______;
(4)非负整数包括________和_______又称为_______.
负分数
自然数
例4:下图中的两个圆分别表示正数集合和分数集合,请你在每个圆中及它们重叠的部分各填入3个数;
正数集合
分数集合
正数
0
负数
0
0
正整数
正分数集合
*
做一做:将下列各数分别填入相应的集合中;
正整数集合
负分数集合
正有理数集合
非正数集合
*
到现在为止我们学过的数都是有理数(圆周率除外),有理数可以按不同的标准进行分类,标准不同,分类的结果也不同。
有理数的分类:
1、按定义分类:
2、按性质分类:
注意:①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数。
*
课堂作业
课本P14页习题第1,2,4题.
练习1: 在有理数中,不存在( )
A.既是整数,又是负数的数
B.既不是正数,也不是负数的数
C.既是正数,又是负数的数
D.既是分数,又是负数的数
C
练习2:下列说法错误的是( )
A.负整数和负分数统称为负有理数
B.正整数、负整数和0统称为整数
C.正有理数和负有理数统称为有理数
D.0是整数,但不是分数
C
练习3:判断题
(1)任何有限小数都是有理数。( )
(2)任何小数都是有理数。( )
(3)0是最小的有理数。( )
(4)有理数不是正数就是负数。( )
(5)存在着最小的自然数。( )
引导:(1)任何有限小数都是有理数,所以正确。
(2)任何有限小数都是有理数,所以错误。
(3)有理数没有最小的,所以错误。
(4)有理数还包括0,所以错误。
(5)存在着最小的自然数0,所以正确。
练习4:下面关于有理数的说法正确的是( )
A.有理数可以分为正有理数和负有理数两大类;
B.正整数集合和负整数集合合在一起就构成整数集合;
C.整数和分数统称为有理数;
D.正数、负数和零统称为有理数。
C
C
2001,
0,2001,
课堂练习
第一排,1个数;
第二排,3个数;
第三排,5个数;
第四排,7个数;
第n排,2n-1个数;
探究规律
课堂练习
按照上述规律排下去,第5行从左边起第4个数是 ; 第6行从右边起第4个数是 ;第10行从左边起第9个数是 ;-51排在第 行从左边起第 个数。
第n排,2n-1个数;
20
-33
90
8
2
*
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
*
上节课我们学习了什么内容
1正数与负数
2零既不是正数也不是负数
3正数和负数是表示具有相反意义的量
4零表示的意义
5实际生活中,通常用正负数表示允许误差
*
1 明白有理数的概念,知道有理数的分类,体会分类思想的应用。
2 知道集合的概念,会将有理数按要求分类。
3 在学习过程中,积累学习数学的方法,激发学习数学的热情。
学习目标
学习重点
有理数的分类
*
练一练 学一学
依据生活小常识回答问题
1.小明家养了一群小鸡,没事的时候小明在家数小鸡,所得的数是属于什么数?
正数
2.在你的刻度尺上可以读出哪几类有理数?
正数 0 分数
3.蔬菜大棚里的温度计上,能读出哪几类有理数?
正数 零 负数
*
12.96,
182.5,
110,
12.91,
1.1,
-52
0,
+75,
122.5,
+10.
-7.5,
18,
305,
1.在上面各数中,哪些是在小学里学过的数 它们可以分为哪几类
2.在上面的数中,哪些数不是小学所学的数 .
3.计算下列各分数的值,说明所有分数都可以化作什么数
探究1
4.由前面的结论,小学里学的数可以分为哪几类
5.引入负数后,整数除了小学学的整数外,还包含其它的整数吗?
分数除了小学学的分数外,还包含其它的分数吗?
分数均可化为有限小数和无限循环小数.
*
到目前为止,我们学过的数可以分为以下几类?
正整数:如1,2,3,…;
零:0;
负整数:如-1,-2,-3,…;
正分数:如
负分数:如
1、正整数、0和负整数统称为整数;
2、正分数、负分数统称为分数;
3、整数和分数统称为有理数;
*
正整数 零 负整数统称整数
正分数和负分数统称分数
整数和分数统称有理数
*
(整数和分数)
有理数
______
______
______
______
______
______
______
整数
分数
正整数
0
负整数
正分数
负分数
1、按定义分类:
*
有理数分类的几点注意:
1,如 能约分成整数的数_____(填“能”或“不能”)算做分数;
不能
2,无限不循环小数不是有理数;
3,整数中除了正整数和负整数,还有_____.
0
有理数还有其他的分类方法吗?
*
有理数
______
______
______
______
______
______
______
正数
0
负数
正整数
正分数
负整数
负分数
2、按性质分类:
注意:①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
(正数、0和负数)
1.在左面的有理数中,
正整数有:__________;
负分数有:_____________________________;整数有:_______________________________;分数有:_______________________________.
探究有理数的分类(二)
小组讨论,合作完成讨论题,集中交流,形成正确分类方法,学生画出分类示意图,同桌合作画出与分类对应的有理数树.
2.丹丹在做第1题时,发现了新的分类方法,她认为:带“+”的数分为一类,带“-”的数分为一类,数的前面没有符号的作为一类.你认为她的分类方法对吗 若不对,你发现什么新的分类方法吗
探究2
-
新知讲解
数集
定义:把一些数放在一起,就组成一类数的集合,简称数集。
所有有理数组成的数集叫做有理数集;
所有整数组成的数集叫做整数集;
所有正数组成的数集叫做正数集;
所有负数组成的数集叫做负数集;
若按集合分类,则每个集合最后要加上“…”。
注意:
一类数的集合必须是符合条件的所有数,不能遗漏。
若一类数的集合有无数个数,则表示这个数的集合时,除写上题中给定的有限个数之外,必须加上省略号。
*
例1:把下列各数填在相应的集合中:
正数集合:{ };
负数集合:{ };
分数集合:{ };
整数集合:{ };
非负有理数集合:{ };
有理数集合:{ };
注意:1.像 这种可以先化简成整数的数是整数不是分数;
2.所有小数归为分数.
把下列各数填入它所属于的集合的圈内:
15, , , , ,
-0.1, , , -123,2.33.
正分数集合 负整数集合
正整数集合 负分数集合
以上四个集合能组成有理数集合吗?
随堂练习
-
*
例2,下列说法正确的是 ( )
A.非负有理数就是正有理数
B. 0仅表示没有,是有理数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数
D
练习:判断正误
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
*
例3 :填空
(1)既是分数又是负数的数是_______;
(2)非负数包括________和_______;
(3)非正数包括________和_______;
(4)非负整数包括________和_______又称为_______.
负分数
自然数
例4:下图中的两个圆分别表示正数集合和分数集合,请你在每个圆中及它们重叠的部分各填入3个数;
正数集合
分数集合
正数
0
负数
0
0
正整数
正分数集合
*
做一做:将下列各数分别填入相应的集合中;
正整数集合
负分数集合
正有理数集合
非正数集合
*
到现在为止我们学过的数都是有理数(圆周率除外),有理数可以按不同的标准进行分类,标准不同,分类的结果也不同。
有理数的分类:
1、按定义分类:
2、按性质分类:
注意:①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③零是整数,但零既不是正数,也不是负数.
几种常用整数和分数名词的含义:
(1)正整数:既是正数,又是整数的数;
(2)负整数:既是负数,又是整数的数;
(3)正分数:既是正数,又是分数的数;
(4)负分数:既是负数,又是分数的数;
(5)非负整数:正整数和0;
(6)非正整数:0和负整数。
*
课堂作业
课本P14页习题第1,2,4题.
练习1: 在有理数中,不存在( )
A.既是整数,又是负数的数
B.既不是正数,也不是负数的数
C.既是正数,又是负数的数
D.既是分数,又是负数的数
C
练习2:下列说法错误的是( )
A.负整数和负分数统称为负有理数
B.正整数、负整数和0统称为整数
C.正有理数和负有理数统称为有理数
D.0是整数,但不是分数
C
练习3:判断题
(1)任何有限小数都是有理数。( )
(2)任何小数都是有理数。( )
(3)0是最小的有理数。( )
(4)有理数不是正数就是负数。( )
(5)存在着最小的自然数。( )
引导:(1)任何有限小数都是有理数,所以正确。
(2)任何有限小数都是有理数,所以错误。
(3)有理数没有最小的,所以错误。
(4)有理数还包括0,所以错误。
(5)存在着最小的自然数0,所以正确。
练习4:下面关于有理数的说法正确的是( )
A.有理数可以分为正有理数和负有理数两大类;
B.正整数集合和负整数集合合在一起就构成整数集合;
C.整数和分数统称为有理数;
D.正数、负数和零统称为有理数。
C
C
2001,
0,2001,
课堂练习
第一排,1个数;
第二排,3个数;
第三排,5个数;
第四排,7个数;
第n排,2n-1个数;
探究规律
课堂练习
按照上述规律排下去,第5行从左边起第4个数是 ; 第6行从右边起第4个数是 ;第10行从左边起第9个数是 ;-51排在第 行从左边起第 个数。
第n排,2n-1个数;
20
-33
90
8
2
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
