2.10 有理数的除法 课件(共21张PPT)
文档属性
| 名称 | 2.10 有理数的除法 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第2章 有理数
2.10 有理数的除法
华师版数学七年级上册
教学过程
温故知新
1
2
3
4
5
探究发现
合作交流
归纳总结
课堂检测
几个不等于0的数相乘,积的符号由负因数的个数决定。当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
几个数相乘,有一个因数为0,积就为0。
有理数的乘法法则
注意
运算过程中应先判断积的符号。
温故知新
温故知新
答:已知两个数的积和一个因数,求另一个因数。
除法与乘法是互逆运算关系。
2、小学学习过的倒数的意义是什么?
答:如果两个数的乘积为1,那么这两个数互为倒数。
1、小学里学习过除法的意义是什么?它与乘法有什么关系?
注意:零没有倒数哟!
3、根据乘法法则口答下列各题:
(1)(-3)×4=_______; (2)3×(-)=____;
(3)(-9)×(-3)=____; (4)0×(-2)=____;
-12
-1
27
0
开始抢答啦!
4
-3
-25
3
0
4
-3
3
-25
0
已知积和其中一个因数,求另一个因数。
积÷因数=另一个因数
除法是乘法的逆运算
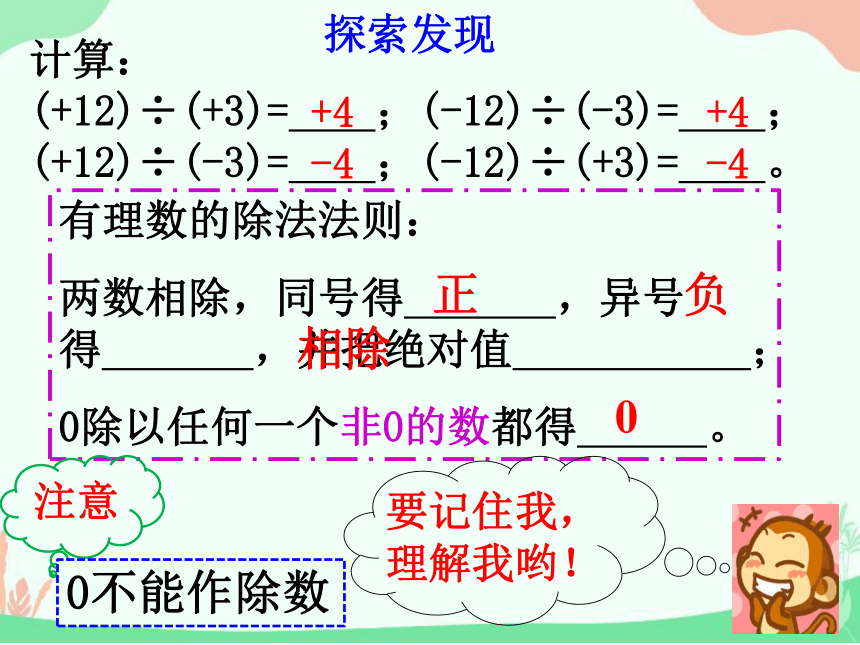
探索发现
有理数的除法法则:
两数相除,同号得 ,异号得 ,并把绝对值 ;
0除以任何一个非0的数都得 。
注意
0不能作除数
正
负
相除
0
计算:
(+12)÷(+3)= ;(-12)÷(-3)= ;
(+12)÷(-3)= ;(-12)÷(+3)= 。
+4
+4
-4
-4
要记住我,理解我哟!
探索发现
*
定义:
如果两个数的乘积等于1,那么这两个数叫做互为倒数 。
写出下列数的倒数:
小学里学过的倒数的意义,什么叫倒数
做一做:教材P55,练习第1题
归纳:1.除0外所有有理数都有倒数;
2.倒数等于本身的是1与-1;
3.正数倒数是正数,负数倒数是负数。
对有理数仍有:乘积为1的两个数互为倒数。
用式子表示就是:
=
=
=
除以一个数等于乘以这个数的倒数
解:原式
解:原式
计算——
*
例1 计算:
从结果看你发现了什么?
解:
有理数除法法则:
两数相除,同号得正,异号得负,并把绝对值相除。
零除以任何一个不等于零的数,都得零。
做一做:教材P55,练习第2题
*
例2.化简下列分数:
解
做一做:教材P56,习题第3题和第6题
1、填空:
(1) 的倒数是-2, -0.1的倒数是 。
(2)-6的倒数是 ,相反数是 。
(3) 的倒数等于它本身, 的相反数等于它本
身, 的绝对值等于它本身。
(4)若一个数的相反数与这个数的倒数的和等于0,则这
个数是 。
-10
6
0
非负数
课堂检测
*
例3 计算下列各题
解:
原式
原式
教材P55,练习第3题
做一做:
2、两个互为相反数的有理数相除,商为( )
A.正数 B.负数 C.不存在 D.负数或不存在
D
3、两个有理数的商是正数,则( )
A.它们的和为正数 B.它们的和为负数
C.至少有一个数为正数 D.它们的积为正数
D
课堂检测
*
设a、b、c为非零有理数,求下列式子的值
分四种情况分类讨论——
②当a、b、c都是负数时,原式=-3
③当a、b、c中有两个正数,一个负数时,原式=1
④当a、b、c中有两个负数,一个正数时,原式=-1
∴ 综上所述,原式的值为±1,或±3。
①当a、b、c都是正数时,原式=3
6÷(-3)=-2
新知识
旧知识
转化
小 结
互为倒数
相同的结果
-3
6×(- )=-2
1
3
1
3
-
*
本节课里我的收获是……
除以一个数等于乘以这个数的倒数。
两数相除,同号得正,异号得负,并把
绝对值相除。
零除以任何一个不等于零的数,都得零。
有理数除法法则——
-a的倒数是- (a≠0),
- 的倒数是- ( p≠0,q≠0)
a
1
q
p
p
q
*
1.课本P56页,习题2.10第1,2,4
2.补充:
作 业
谢 谢 大 家
第2章 有理数
2.10 有理数的除法
华师版数学七年级上册
教学过程
温故知新
1
2
3
4
5
探究发现
合作交流
归纳总结
课堂检测
几个不等于0的数相乘,积的符号由负因数的个数决定。当负因数有奇数个时,积为负;当负因数有偶数个时,积为正。
几个数相乘,有一个因数为0,积就为0。
有理数的乘法法则
注意
运算过程中应先判断积的符号。
温故知新
温故知新
答:已知两个数的积和一个因数,求另一个因数。
除法与乘法是互逆运算关系。
2、小学学习过的倒数的意义是什么?
答:如果两个数的乘积为1,那么这两个数互为倒数。
1、小学里学习过除法的意义是什么?它与乘法有什么关系?
注意:零没有倒数哟!
3、根据乘法法则口答下列各题:
(1)(-3)×4=_______; (2)3×(-)=____;
(3)(-9)×(-3)=____; (4)0×(-2)=____;
-12
-1
27
0
开始抢答啦!
4
-3
-25
3
0
4
-3
3
-25
0
已知积和其中一个因数,求另一个因数。
积÷因数=另一个因数
除法是乘法的逆运算
探索发现
有理数的除法法则:
两数相除,同号得 ,异号得 ,并把绝对值 ;
0除以任何一个非0的数都得 。
注意
0不能作除数
正
负
相除
0
计算:
(+12)÷(+3)= ;(-12)÷(-3)= ;
(+12)÷(-3)= ;(-12)÷(+3)= 。
+4
+4
-4
-4
要记住我,理解我哟!
探索发现
*
定义:
如果两个数的乘积等于1,那么这两个数叫做互为倒数 。
写出下列数的倒数:
小学里学过的倒数的意义,什么叫倒数
做一做:教材P55,练习第1题
归纳:1.除0外所有有理数都有倒数;
2.倒数等于本身的是1与-1;
3.正数倒数是正数,负数倒数是负数。
对有理数仍有:乘积为1的两个数互为倒数。
用式子表示就是:
=
=
=
除以一个数等于乘以这个数的倒数
解:原式
解:原式
计算——
*
例1 计算:
从结果看你发现了什么?
解:
有理数除法法则:
两数相除,同号得正,异号得负,并把绝对值相除。
零除以任何一个不等于零的数,都得零。
做一做:教材P55,练习第2题
*
例2.化简下列分数:
解
做一做:教材P56,习题第3题和第6题
1、填空:
(1) 的倒数是-2, -0.1的倒数是 。
(2)-6的倒数是 ,相反数是 。
(3) 的倒数等于它本身, 的相反数等于它本
身, 的绝对值等于它本身。
(4)若一个数的相反数与这个数的倒数的和等于0,则这
个数是 。
-10
6
0
非负数
课堂检测
*
例3 计算下列各题
解:
原式
原式
教材P55,练习第3题
做一做:
2、两个互为相反数的有理数相除,商为( )
A.正数 B.负数 C.不存在 D.负数或不存在
D
3、两个有理数的商是正数,则( )
A.它们的和为正数 B.它们的和为负数
C.至少有一个数为正数 D.它们的积为正数
D
课堂检测
*
设a、b、c为非零有理数,求下列式子的值
分四种情况分类讨论——
②当a、b、c都是负数时,原式=-3
③当a、b、c中有两个正数,一个负数时,原式=1
④当a、b、c中有两个负数,一个正数时,原式=-1
∴ 综上所述,原式的值为±1,或±3。
①当a、b、c都是正数时,原式=3
6÷(-3)=-2
新知识
旧知识
转化
小 结
互为倒数
相同的结果
-3
6×(- )=-2
1
3
1
3
-
*
本节课里我的收获是……
除以一个数等于乘以这个数的倒数。
两数相除,同号得正,异号得负,并把
绝对值相除。
零除以任何一个不等于零的数,都得零。
有理数除法法则——
-a的倒数是- (a≠0),
- 的倒数是- ( p≠0,q≠0)
a
1
q
p
p
q
*
1.课本P56页,习题2.10第1,2,4
2.补充:
作 业
谢 谢 大 家
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
