2.11 有理数的乘方 课件(共30张PPT)
文档属性
| 名称 | 2.11 有理数的乘方 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 07:14:09 | ||
图片预览










文档简介
(共30张PPT)
2.11 有理数乘方
说故事
“故事大王”讲故事:棋盘上的麦粒
从前有个国王叫舍罕王喜欢打仗,正好宰相西萨· 班·达依尔发明了国际象棋,可以让他在棋盘上过交战的瘾。国王很高兴,准备奖赏宰相。宰相说:“我不要金子,也不要银子,我就要麦子。”国王问:“好,你要多少麦子?”宰相说:“国际象棋盘有64个格,第1格放1粒麦,第2格放2粒麦,第 3格放4粒麦,第4格放8粒麦,第5格放16粒麦,以此类推,每个格的麦粒数是前一格的2倍。” 国王没多想,就答应了。国王吃完饭后就睡着了。等他睡醒后,看见宰相还在宫殿里。国王问:“你怎么还没走?”宰相说:“麦还没装完呢。”国王说:“我觉都 睡醒了,怎么还没装完呢?士兵,装了多少麦了?”士兵说:“咱们粮仓的麦已经被运完一半,才刚到第35格......”国王反悔了,因为他确实没有那么多麦子。你知道有多少粒麦吗?
说故事
《庄子 ·天下篇》:一尺之棰,日取其半,万世不竭。
多个不为0的因数相乘,积的符号如何确定?
简记为:
负因数的个数奇负偶正
计算步骤又是怎样的呢
简记为:先定号,再定量
-8
72
一起来复习
1、(-2)×(-2)×(-2)= ;
2、(-1)×(-2)×(-3)×(-4)×3= ;
6
把带分数化成假分数,小数化成分数把
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张;
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
把一张纸
2×2×2×2×2×2×2×2×2×2张(10个2相乘)
100个2相乘
有更简洁的方式表示这个式子吗?
一起来探索
2个 相加可记为:
4个 相加可记为:
个 相加可记为:
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
3个 相加可记为:
一起来探索
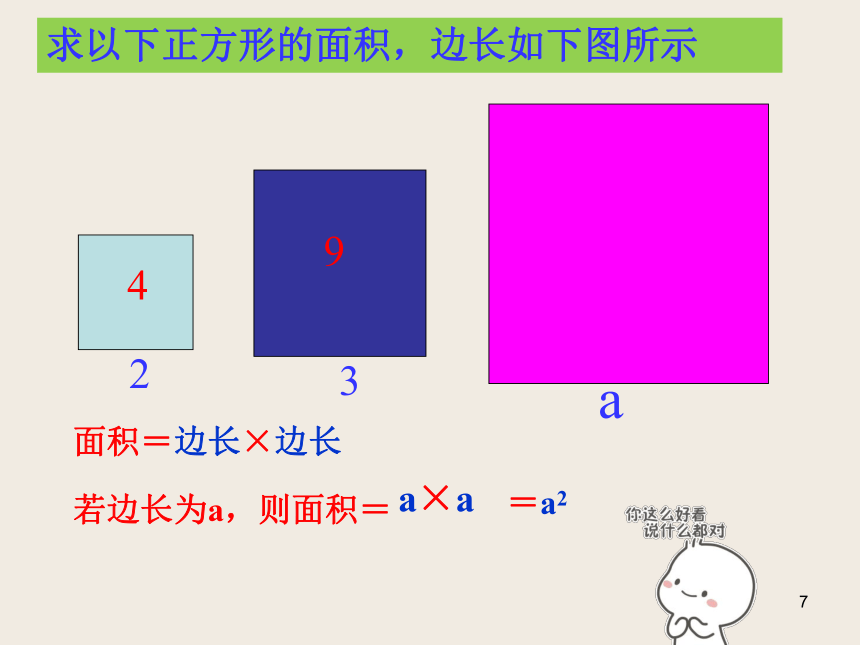
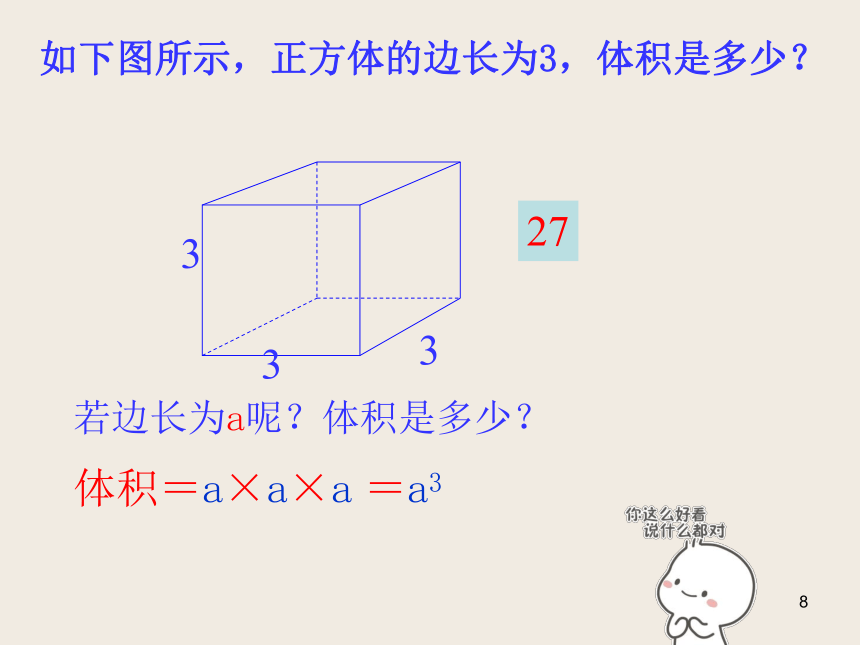
求以下正方形的面积,边长如下图所示23a面积=边长×边长若边长为a,则面积=a×a=a2493如下图所示,正方体的边长为3,体积是多少?若边长为a呢?体积是多少?体积=a×a×a=a33327思考:n个相同的因数a相乘: a×a×a.............×a,又记作什么呢?5个a=ana×aa×a×aa×a×a×aa×a×a×a×a=a2=a3= = a4a5a×a×a.............×an个a做一做,想一想4个a
乘方:
一般地,求n个相同因数a的积的运算。
乘方的结果叫做幂
幂
底数
指数
读作:a的n次方(或a的n次幂)
得出定义,揭示内涵
例如:23中,底数是2,指数是3。
读作2的3次方或2的3次幂。
23和32一样吗?为什么?
想
一
想
2×2×2×2=24
2×2=22
2×2×2=23
2×2···×2×2=210
10个2
2×2···×2×2=2n
n个2
2=21
问:数8有没有指数,如果有你能说出它的指数吗?那a呢?
一个数可以看作这个数本身的一次方
例如:8就是81,a是a1。
通常指数1可以省略不写
例1.指出它们的指数与底数,及其他们的读法。
(1)在64中,底数是 ,指数是 ,读作 ;
(2)在a7中,底数是 ,指数是 ,读作 ;
(3)在(-4)3中,底数是 ,指数是 ,读作 ;
(4)在(-0.1)10中,底数是 ,指数是 ,读作 ;
(5)在(- )5中,底数是 ,指数是 ,读作 ;
(6)在8中,底数是 ,指数是 ;
6
4
a
7
-4
3
-0.1
5
10
8
1
6的4次幂
a的7次幂
-4的3次幂
-0.1的10次幂
的5次幂
例2:把下列各式写成乘方的形式:注意:对于负数和分数的乘方需要给底数加上括号。例3.把下列各式写成乘法的形式:=;1.在中,12叫__,10叫做__,读作:____,2.在 中,底数是__,指数是__,读作:____底数指数12的10次方7做一做一.填空3.在中,底数是_,指数是__,读作:______,4.在中,底数是__,指数是__,读作:____,3163的16次方的相反数-317-3的17次方二.把下列乘法式子写成乘方的形式:1. 1×1×1×1×1×1×1=;2. 3×3×3×3×3=;3.(-3)×(-3)×(-3)×(-3)=;1735(-3)4
···
···
例4.(1)计算,填表
例4.(2)通过计算的结果,发现了什么?
···
···
幂的符
号法则
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何非零次幂都是0.
习题1.确定下列幂的正负,说明理由。
+
+
+
-
-
-
习题2.(1)找一找,谁是我的好朋友?
习题2.(2)找一找,谁是我的好朋友?
习题2.(3)找一找,谁是我的好朋友?
习题3.练习,计算。
解:
解:
解:
解:
思考:表示3的2次幂的相反数表示-3的2次幂计算结果为-9计算结果为9表示2的2次幂与3的商表示2/3的2次幂表示2的3次幂计算结果为8表示3的2次幂计算结果为9讨论:1.4的平方得多少?2.-4的平方得多少?3.平方等于16的数有几个?4.有没有平方得-16的有理数?答:(1)4的平方是16(2)-4的平方是16(3)平方得16的数有两个4和-4(4)没有,有理数的平方都是正数你能发现什么吗?1.互为相反数的两个数的平方相等.即:若a=b,则a2=b2。2.一个数平方结果为非负数.即:a2≥0。3.两个数的平方相等,则这两个数相等或互为相反数。做一做:教材P58,练习第1,2题例5:已知:∣a-1∣+ (b+1)2=0,求:a2004+b2005的值。解:由题意可知:a-1=0b+1=0解得:a=1b=-1∴ 原式=12004+ (-1)2005=1+ (-1)=0∴ 原式的值为0。练习:已知:∣a+2∣ + (b+3)2=0。求:a2+b3的值。
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条。如图所示:
这样捏合到第 6次后可拉出 根面条。
64
n次拉伸后有 根面条
数学与生活
一杯咖啡,第一次喝掉一半,第二次喝掉剩下的一半,如此下去......,请问:第3次喝掉多少?还剩下多少?
第n次喝掉多少?还剩多少?
n次总共喝掉多少?还剩下多少?
数形结合思想
数学与生活
1、乘方、幂、底数和指数的定义an幂指数底数2、有理数乘法法则正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数本节课里我的收获是……简记为:奇负偶正4、乘方是特殊的乘法运算3、乘方运算的步骤:先定号,再定量一.课本P58页,习题2.11 1、3、4二.补充:布置作业,引导预习2.已知:∣a+3∣+ (b-4)2=0。求:3a-5b的值。
谢 谢 大 家
2.11 有理数乘方
说故事
“故事大王”讲故事:棋盘上的麦粒
从前有个国王叫舍罕王喜欢打仗,正好宰相西萨· 班·达依尔发明了国际象棋,可以让他在棋盘上过交战的瘾。国王很高兴,准备奖赏宰相。宰相说:“我不要金子,也不要银子,我就要麦子。”国王问:“好,你要多少麦子?”宰相说:“国际象棋盘有64个格,第1格放1粒麦,第2格放2粒麦,第 3格放4粒麦,第4格放8粒麦,第5格放16粒麦,以此类推,每个格的麦粒数是前一格的2倍。” 国王没多想,就答应了。国王吃完饭后就睡着了。等他睡醒后,看见宰相还在宫殿里。国王问:“你怎么还没走?”宰相说:“麦还没装完呢。”国王说:“我觉都 睡醒了,怎么还没装完呢?士兵,装了多少麦了?”士兵说:“咱们粮仓的麦已经被运完一半,才刚到第35格......”国王反悔了,因为他确实没有那么多麦子。你知道有多少粒麦吗?
说故事
《庄子 ·天下篇》:一尺之棰,日取其半,万世不竭。
多个不为0的因数相乘,积的符号如何确定?
简记为:
负因数的个数奇负偶正
计算步骤又是怎样的呢
简记为:先定号,再定量
-8
72
一起来复习
1、(-2)×(-2)×(-2)= ;
2、(-1)×(-2)×(-3)×(-4)×3= ;
6
把带分数化成假分数,小数化成分数把
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张;
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
把一张纸
2×2×2×2×2×2×2×2×2×2张(10个2相乘)
100个2相乘
有更简洁的方式表示这个式子吗?
一起来探索
2个 相加可记为:
4个 相加可记为:
个 相加可记为:
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
3个 相加可记为:
一起来探索
求以下正方形的面积,边长如下图所示23a面积=边长×边长若边长为a,则面积=a×a=a2493如下图所示,正方体的边长为3,体积是多少?若边长为a呢?体积是多少?体积=a×a×a=a33327思考:n个相同的因数a相乘: a×a×a.............×a,又记作什么呢?5个a=ana×aa×a×aa×a×a×aa×a×a×a×a=a2=a3= = a4a5a×a×a.............×an个a做一做,想一想4个a
乘方:
一般地,求n个相同因数a的积的运算。
乘方的结果叫做幂
幂
底数
指数
读作:a的n次方(或a的n次幂)
得出定义,揭示内涵
例如:23中,底数是2,指数是3。
读作2的3次方或2的3次幂。
23和32一样吗?为什么?
想
一
想
2×2×2×2=24
2×2=22
2×2×2=23
2×2···×2×2=210
10个2
2×2···×2×2=2n
n个2
2=21
问:数8有没有指数,如果有你能说出它的指数吗?那a呢?
一个数可以看作这个数本身的一次方
例如:8就是81,a是a1。
通常指数1可以省略不写
例1.指出它们的指数与底数,及其他们的读法。
(1)在64中,底数是 ,指数是 ,读作 ;
(2)在a7中,底数是 ,指数是 ,读作 ;
(3)在(-4)3中,底数是 ,指数是 ,读作 ;
(4)在(-0.1)10中,底数是 ,指数是 ,读作 ;
(5)在(- )5中,底数是 ,指数是 ,读作 ;
(6)在8中,底数是 ,指数是 ;
6
4
a
7
-4
3
-0.1
5
10
8
1
6的4次幂
a的7次幂
-4的3次幂
-0.1的10次幂
的5次幂
例2:把下列各式写成乘方的形式:注意:对于负数和分数的乘方需要给底数加上括号。例3.把下列各式写成乘法的形式:=;1.在中,12叫__,10叫做__,读作:____,2.在 中,底数是__,指数是__,读作:____底数指数12的10次方7做一做一.填空3.在中,底数是_,指数是__,读作:______,4.在中,底数是__,指数是__,读作:____,3163的16次方的相反数-317-3的17次方二.把下列乘法式子写成乘方的形式:1. 1×1×1×1×1×1×1=;2. 3×3×3×3×3=;3.(-3)×(-3)×(-3)×(-3)=;1735(-3)4
···
···
例4.(1)计算,填表
例4.(2)通过计算的结果,发现了什么?
···
···
幂的符
号法则
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何非零次幂都是0.
习题1.确定下列幂的正负,说明理由。
+
+
+
-
-
-
习题2.(1)找一找,谁是我的好朋友?
习题2.(2)找一找,谁是我的好朋友?
习题2.(3)找一找,谁是我的好朋友?
习题3.练习,计算。
解:
解:
解:
解:
思考:表示3的2次幂的相反数表示-3的2次幂计算结果为-9计算结果为9表示2的2次幂与3的商表示2/3的2次幂表示2的3次幂计算结果为8表示3的2次幂计算结果为9讨论:1.4的平方得多少?2.-4的平方得多少?3.平方等于16的数有几个?4.有没有平方得-16的有理数?答:(1)4的平方是16(2)-4的平方是16(3)平方得16的数有两个4和-4(4)没有,有理数的平方都是正数你能发现什么吗?1.互为相反数的两个数的平方相等.即:若a=b,则a2=b2。2.一个数平方结果为非负数.即:a2≥0。3.两个数的平方相等,则这两个数相等或互为相反数。做一做:教材P58,练习第1,2题例5:已知:∣a-1∣+ (b+1)2=0,求:a2004+b2005的值。解:由题意可知:a-1=0b+1=0解得:a=1b=-1∴ 原式=12004+ (-1)2005=1+ (-1)=0∴ 原式的值为0。练习:已知:∣a+2∣ + (b+3)2=0。求:a2+b3的值。
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条。如图所示:
这样捏合到第 6次后可拉出 根面条。
64
n次拉伸后有 根面条
数学与生活
一杯咖啡,第一次喝掉一半,第二次喝掉剩下的一半,如此下去......,请问:第3次喝掉多少?还剩下多少?
第n次喝掉多少?还剩多少?
n次总共喝掉多少?还剩下多少?
数形结合思想
数学与生活
1、乘方、幂、底数和指数的定义an幂指数底数2、有理数乘法法则正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数本节课里我的收获是……简记为:奇负偶正4、乘方是特殊的乘法运算3、乘方运算的步骤:先定号,再定量一.课本P58页,习题2.11 1、3、4二.补充:布置作业,引导预习2.已知:∣a+3∣+ (b-4)2=0。求:3a-5b的值。
谢 谢 大 家
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
