2.16 有理数复习 课件(共12张PPT)
文档属性
| 名称 | 2.16 有理数复习 课件(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 907.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 07:32:03 | ||
图片预览




文档简介
(共12张PPT)
*
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
*
1、有理数的概念及其分类
整数和分数统称为有理数。
⑴概念:
⑵分类:
有理数
整数
分数
正整数
负整数
0
负分数
正分数
有理数
正有理数
负有理数
正整数
负整数
0
负分数
正分数
⑶注意:
①0既不是正数,也不是负数;0是正数和负数的分界。
②0和正数统称为非负数;0和正整数统称为自然数。
③我们现在所学的数除了 外都是有理数;
我们现在所学的小数都属于分数。
按定义分类
按性质分类
④能约分成整数的数不能算做分数。如:
*
例1把下列各数填在相应的括号里:
整数集{ …}
负数集{ …}
非负整数集{ …}
负分数集{ …}
有理数集{ …}
-7,
2009,
0,
-7,
-5﹪,
2009,
0,
-5﹪,
⑷正数和负数的意义:
表示现实生活中的具有相反意义的两个量
例2 某升降机上升了4m,表示为+4m,那么下降了3m,应记作 。
若规定收入为“+”,则支出-50元表示 。
-3m
收入50元
*
2、数轴
⑴概念:
规定了原点、正方向、单位长度的直线叫做数轴。
数轴三要素
⑵应用:
①任何一个有理数都可以用数轴上的点来表示。
②比较大小:数轴上两个点表示的数,右边的数总比左边数的大。
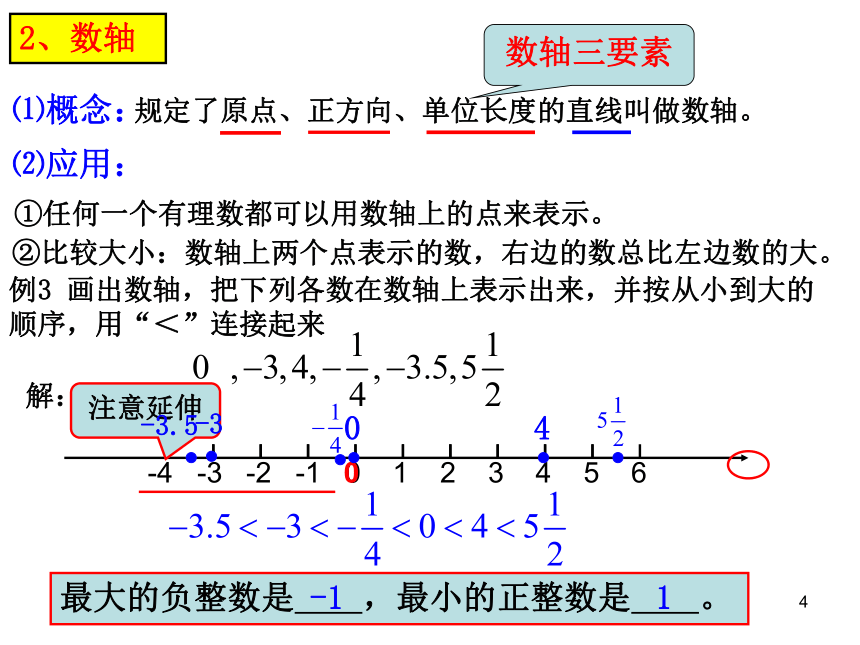
例3 画出数轴,把下列各数在数轴上表示出来,并按从小到大的顺序,用“<”连接起来
-4 -3 -2 -1 0 1 2 3 4 5 6
注意延伸
解:
0
0
-3
4
-3.5
最大的负整数是 ,最小的正整数是 。
-1
1
*
3、相反数
⑴概念:
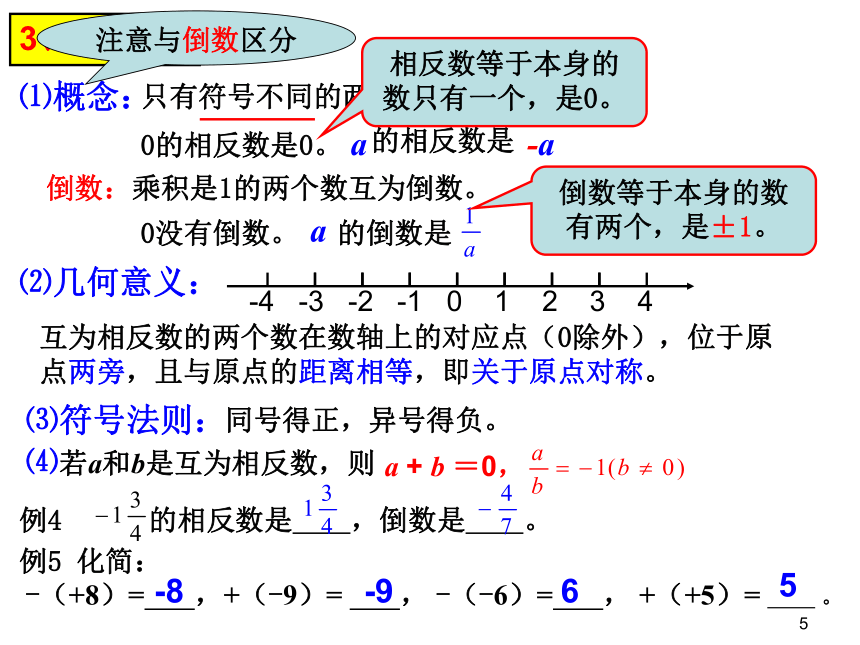
只有符号不同的两个数称为互为相反数。
的相反数是
a
-a
⑵几何意义:
-4 -3 -2 -1 0 1 2 3 4
互为相反数的两个数在数轴上的对应点(0除外),位于原点两旁,且与原点的距离相等,即关于原点对称。
⑶符号法则:
同号得正,异号得负。
0的相反数是0。
相反数等于本身的数只有一个,是0。
注意与倒数区分
倒数:乘积是1的两个数互为倒数。
的倒数是
a
0没有倒数。
倒数等于本身的数有两个,是±1。
⑷若a和b是互为相反数,则
a + b =0,
例4 的相反数是 ,倒数是 。
例5 化简:
-(+8)= ,+(-9)= , -(-6)= , +(+5)= 。
-8
-9
6
5
*
4、绝对值
⑴概念:
在数轴上表示数a的点与原点的距离叫做数a的绝对值。
记作
⑵求法:
|a|=
a
(a>0)
0
(a=0)
-a
(a<0)
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
绝对值等于本身的数有无数个,是非负数。
⑶性质:
①任何一个有理数的绝对值是非负数,即
|a|≥0
两个特殊的非负数:绝对值和平方数
例6 若
2
-3
②互为相反数的两个数绝对值相等。
例7 若|x|=16,则x = ____。
±16
|a – b|表示数轴上数a、b两点间的距离.
⑷应用:
例8 绝对值不大于3的整数有 __个,分别是 。
7
±3、 ±2、 ±1、0
例9 在数轴上与表示-1的点相距4个单位长度的点表示的数是 。
3、-5
*
5、有理数比较大小
⑴利用数轴:数轴上两个点表示的数,右边的数总比左边数的大。
⑵有理数比较法则:
正数大于0,负数小于0,正数大于负数;
两个负数,绝对值大的反而小。
例10 比较大小: (用“>”、“<”或“=”填空)
-3.3 0 , 6 -8 ,0 2,
<
>
<
>
6、科学记数法
⑴a整数位只有一位,即1≤a<10。
⑵正整数n=原数整数数位-1。
例11 用科学记数法表示下列各数:
⑴696000; ⑵354.87; ⑶640万。
例12 的原数是 。
7040000
*
7、准确数与近似数
⑴概念:
下列各选项中的数字是准确数的是( )
A 这本书约有20万字 B 某班学生有54人
C 我市共有200万人口 D 我国的国土面积为960万平方千米
B
⑵精确度:
①精确到哪一位;
②保留几个有效数字(从左边第一个不是0的数起,到末位数字为止,所有的数字叫做有效数字);
例13 下列有四舍五入法得到的近似数,各精确到哪一位?各有 哪几个有效数字?
⑴132.4;⑵0.0572;⑶2.50万;⑷ 。
例14 用四舍五入法,按括号中的要求把下列各数取近似数:
⑴0.34082(精确到千分位); ⑵54.973(精确到0.1); ⑶0.0692(保留两个有效数字);⑷30542(保留3个有效数字)
有效数字:从一个数的左边第一个非0数字起,到末位数字止,所有的数字都是这个数的有效数字。
简单的说:把一个数字前面的0都去掉,从第一个正整数到精确的数位止所有的都是有效数字了。
如:0.0109,前面两个0不是有效数字,后面的109均为有效数字(注意,中间的0也算)。
3.109×105(3.109乘以10的5次方)中,3 1 0 9均为有效数字,后面的10的5次方不是有效数字。
5.2×106,只有5和2是有效数字。
0.0230,前面的两个0不是有效数字,后面的230均为有效数字(后面的0也算)。
1.20 有3个有效数字。
1100.120 有7位有效数字。
*
8、有理数的运算
加法、减法、乘法、除法、乘方
⑴加法:
先确定符号,再确定绝对值。
①同号两数相加,取相同的符号,并把绝对值相加。
(-2)+(-5)
②异号两数相加,取绝对值大的数的符号,并用较大的绝对值减去较小的绝对值。
=-7
(-2)+5
= 3
③互为相反数的两个数相加得0。
(-2)+2=0
④一个数同0相加,仍得这个数。
(-2)+0=-2
⑵减法:
减去一个数,等于加上这个数的相反数。
5-(-2)
=5+2=7
⑶乘法:
③几个不为0的数相乘,当负因数有奇数个时,积为负; 当负因数有偶数个时,积为正。
①两数相乘,同号得正,异号得负,并把绝对值相乘。
②任何数与0相乘,都得0。
(-2)×5
= -10
(-2)×(-3)
= 6
*
⑷除法:
①除以一个数等于乘以这个数的倒数。
②两数相除,同号得正,异号得负,并把绝对值相除。
(-10)÷5
= -2
(-12)÷(-3)
= 4
③0除以任何一个不为0的数,都得0。
例12 化简下列分数:
⑸乘方:
①概念:
求几个相同因数的积的运算,叫做乘方。
②求法:
乘方运算可以化为乘法运算进行:
③符号法则:
正数的任何次幂都是正数。
负数的奇数次幂是负数,偶数次幂是正数。
0的任何次幂都是0。
例13 计算:
=9
=-8
=-9
负数和分数的乘方书写时,一定要把整个负数和分数用小括号括起来。
*
⑹有理数混合运算:
①注意运算顺序
ⅰ先算乘方,再算乘除,最后算加减;
ⅱ同级运算,按照从左至右的顺序进行;
ⅲ如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
②巧用运算律
ⅰ加法交换律和结合律
Ⅱ正负数分别结合相加;
Ⅰ互为相反数结合相加;
Ⅲ能凑整数的数相结合;
Ⅳ同分母或易于通分的分数相结合
ⅱ乘法分配律
Ⅰ正用分配律:a(b+c)=ab+ac;
Ⅱ反用分配律:ab+ac=a(b+c);
例14 计算:
谢 谢 大 家
*
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
*
1、有理数的概念及其分类
整数和分数统称为有理数。
⑴概念:
⑵分类:
有理数
整数
分数
正整数
负整数
0
负分数
正分数
有理数
正有理数
负有理数
正整数
负整数
0
负分数
正分数
⑶注意:
①0既不是正数,也不是负数;0是正数和负数的分界。
②0和正数统称为非负数;0和正整数统称为自然数。
③我们现在所学的数除了 外都是有理数;
我们现在所学的小数都属于分数。
按定义分类
按性质分类
④能约分成整数的数不能算做分数。如:
*
例1把下列各数填在相应的括号里:
整数集{ …}
负数集{ …}
非负整数集{ …}
负分数集{ …}
有理数集{ …}
-7,
2009,
0,
-7,
-5﹪,
2009,
0,
-5﹪,
⑷正数和负数的意义:
表示现实生活中的具有相反意义的两个量
例2 某升降机上升了4m,表示为+4m,那么下降了3m,应记作 。
若规定收入为“+”,则支出-50元表示 。
-3m
收入50元
*
2、数轴
⑴概念:
规定了原点、正方向、单位长度的直线叫做数轴。
数轴三要素
⑵应用:
①任何一个有理数都可以用数轴上的点来表示。
②比较大小:数轴上两个点表示的数,右边的数总比左边数的大。
例3 画出数轴,把下列各数在数轴上表示出来,并按从小到大的顺序,用“<”连接起来
-4 -3 -2 -1 0 1 2 3 4 5 6
注意延伸
解:
0
0
-3
4
-3.5
最大的负整数是 ,最小的正整数是 。
-1
1
*
3、相反数
⑴概念:
只有符号不同的两个数称为互为相反数。
的相反数是
a
-a
⑵几何意义:
-4 -3 -2 -1 0 1 2 3 4
互为相反数的两个数在数轴上的对应点(0除外),位于原点两旁,且与原点的距离相等,即关于原点对称。
⑶符号法则:
同号得正,异号得负。
0的相反数是0。
相反数等于本身的数只有一个,是0。
注意与倒数区分
倒数:乘积是1的两个数互为倒数。
的倒数是
a
0没有倒数。
倒数等于本身的数有两个,是±1。
⑷若a和b是互为相反数,则
a + b =0,
例4 的相反数是 ,倒数是 。
例5 化简:
-(+8)= ,+(-9)= , -(-6)= , +(+5)= 。
-8
-9
6
5
*
4、绝对值
⑴概念:
在数轴上表示数a的点与原点的距离叫做数a的绝对值。
记作
⑵求法:
|a|=
a
(a>0)
0
(a=0)
-a
(a<0)
正数的绝对值是它本身
0的绝对值是0
负数的绝对值是它的相反数
绝对值等于本身的数有无数个,是非负数。
⑶性质:
①任何一个有理数的绝对值是非负数,即
|a|≥0
两个特殊的非负数:绝对值和平方数
例6 若
2
-3
②互为相反数的两个数绝对值相等。
例7 若|x|=16,则x = ____。
±16
|a – b|表示数轴上数a、b两点间的距离.
⑷应用:
例8 绝对值不大于3的整数有 __个,分别是 。
7
±3、 ±2、 ±1、0
例9 在数轴上与表示-1的点相距4个单位长度的点表示的数是 。
3、-5
*
5、有理数比较大小
⑴利用数轴:数轴上两个点表示的数,右边的数总比左边数的大。
⑵有理数比较法则:
正数大于0,负数小于0,正数大于负数;
两个负数,绝对值大的反而小。
例10 比较大小: (用“>”、“<”或“=”填空)
-3.3 0 , 6 -8 ,0 2,
<
>
<
>
6、科学记数法
⑴a整数位只有一位,即1≤a<10。
⑵正整数n=原数整数数位-1。
例11 用科学记数法表示下列各数:
⑴696000; ⑵354.87; ⑶640万。
例12 的原数是 。
7040000
*
7、准确数与近似数
⑴概念:
下列各选项中的数字是准确数的是( )
A 这本书约有20万字 B 某班学生有54人
C 我市共有200万人口 D 我国的国土面积为960万平方千米
B
⑵精确度:
①精确到哪一位;
②保留几个有效数字(从左边第一个不是0的数起,到末位数字为止,所有的数字叫做有效数字);
例13 下列有四舍五入法得到的近似数,各精确到哪一位?各有 哪几个有效数字?
⑴132.4;⑵0.0572;⑶2.50万;⑷ 。
例14 用四舍五入法,按括号中的要求把下列各数取近似数:
⑴0.34082(精确到千分位); ⑵54.973(精确到0.1); ⑶0.0692(保留两个有效数字);⑷30542(保留3个有效数字)
有效数字:从一个数的左边第一个非0数字起,到末位数字止,所有的数字都是这个数的有效数字。
简单的说:把一个数字前面的0都去掉,从第一个正整数到精确的数位止所有的都是有效数字了。
如:0.0109,前面两个0不是有效数字,后面的109均为有效数字(注意,中间的0也算)。
3.109×105(3.109乘以10的5次方)中,3 1 0 9均为有效数字,后面的10的5次方不是有效数字。
5.2×106,只有5和2是有效数字。
0.0230,前面的两个0不是有效数字,后面的230均为有效数字(后面的0也算)。
1.20 有3个有效数字。
1100.120 有7位有效数字。
*
8、有理数的运算
加法、减法、乘法、除法、乘方
⑴加法:
先确定符号,再确定绝对值。
①同号两数相加,取相同的符号,并把绝对值相加。
(-2)+(-5)
②异号两数相加,取绝对值大的数的符号,并用较大的绝对值减去较小的绝对值。
=-7
(-2)+5
= 3
③互为相反数的两个数相加得0。
(-2)+2=0
④一个数同0相加,仍得这个数。
(-2)+0=-2
⑵减法:
减去一个数,等于加上这个数的相反数。
5-(-2)
=5+2=7
⑶乘法:
③几个不为0的数相乘,当负因数有奇数个时,积为负; 当负因数有偶数个时,积为正。
①两数相乘,同号得正,异号得负,并把绝对值相乘。
②任何数与0相乘,都得0。
(-2)×5
= -10
(-2)×(-3)
= 6
*
⑷除法:
①除以一个数等于乘以这个数的倒数。
②两数相除,同号得正,异号得负,并把绝对值相除。
(-10)÷5
= -2
(-12)÷(-3)
= 4
③0除以任何一个不为0的数,都得0。
例12 化简下列分数:
⑸乘方:
①概念:
求几个相同因数的积的运算,叫做乘方。
②求法:
乘方运算可以化为乘法运算进行:
③符号法则:
正数的任何次幂都是正数。
负数的奇数次幂是负数,偶数次幂是正数。
0的任何次幂都是0。
例13 计算:
=9
=-8
=-9
负数和分数的乘方书写时,一定要把整个负数和分数用小括号括起来。
*
⑹有理数混合运算:
①注意运算顺序
ⅰ先算乘方,再算乘除,最后算加减;
ⅱ同级运算,按照从左至右的顺序进行;
ⅲ如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
②巧用运算律
ⅰ加法交换律和结合律
Ⅱ正负数分别结合相加;
Ⅰ互为相反数结合相加;
Ⅲ能凑整数的数相结合;
Ⅳ同分母或易于通分的分数相结合
ⅱ乘法分配律
Ⅰ正用分配律:a(b+c)=ab+ac;
Ⅱ反用分配律:ab+ac=a(b+c);
例14 计算:
谢 谢 大 家
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
