4.6.3 余角和补角 课件(共19张PPT)
文档属性
| 名称 | 4.6.3 余角和补角 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 922.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 07:44:02 | ||
图片预览




文档简介
(共19张PPT)
3 余角和补角
1.认识角的两种特殊关系:
互余、互补
2.掌握角的两个性质:
同角或等角的余角相等
同角或等角的补角相等
自学课本P152页思考以下问题:
1.互为余角的定义;
2.互为补角的定义;
3.互余,互补是指几个角的关系?
4.互为余角,互为补角的角与角的位置有关吗?它们是否必须有公共顶点,公共边?
5.说说互余,互补的区别和共同之处
6.如何用数学语言表述两个角互余,互补.
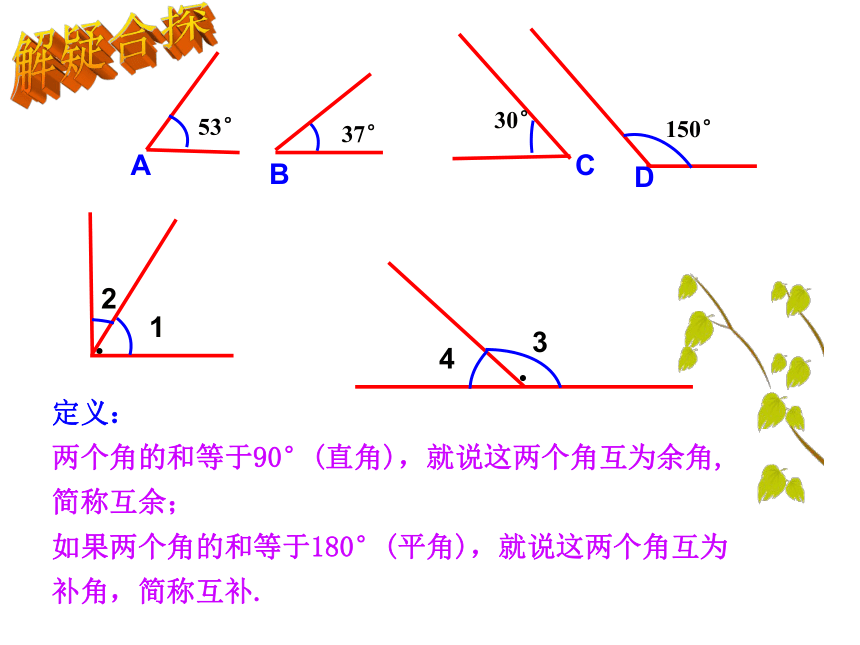
30°
150°
·
3
4
定义:
两个角的和等于90°(直角),就说这两个角互为余角,
简称互余;
如果两个角的和等于180°(平角),就说这两个角互为
补角,简称互补.
37°
53°
·
1
2
A
B
C
D
请同学们比较互补与互余的概念,说说它们的区别和
共同之处?
区别:互余是两个角的和是直角,互补是两个角的和
是平角.
相同:(1)互余和互补都是对两个角而言;
(2)不管这两个角在什么位置,只要满足两角和是
90度(180度),它们都互余(补)
(角的数量特点)
1
2
2
1
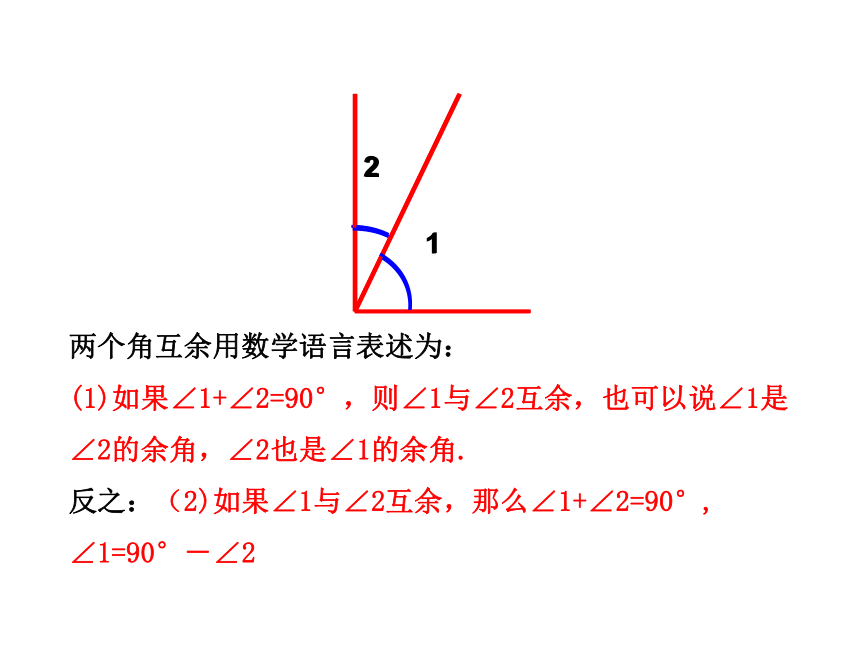
两个角互余用数学语言表述为:
(1)如果∠1+∠2=90°,则∠1与∠2互余,也可以说∠1是∠2的余角,∠2也是∠1的余角.
反之:(2)如果∠1与∠2互余,那么∠1+∠2=90°,
∠1=90°-∠2
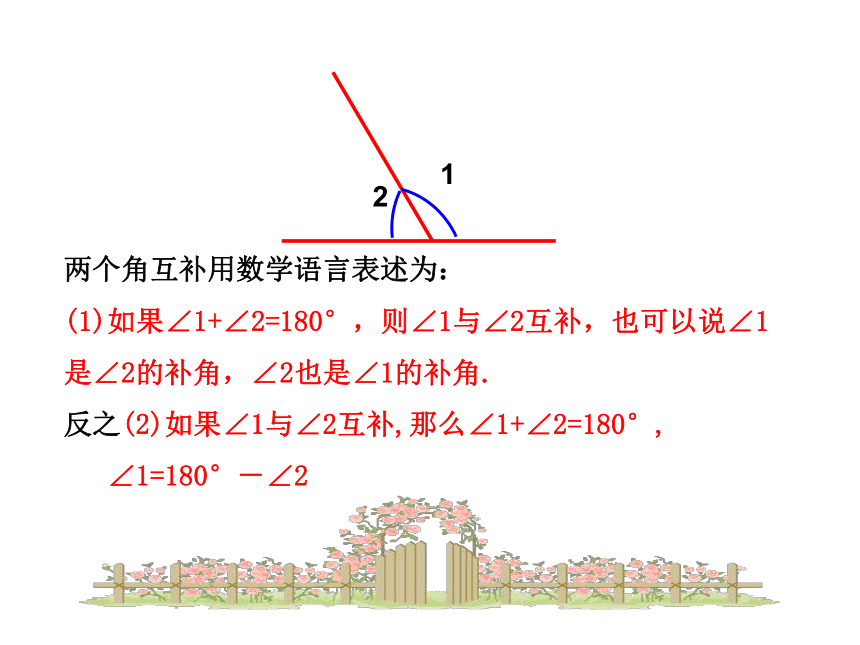
两个角互补用数学语言表述为:
(1)如果∠1+∠2=180°,则∠1与∠2互补,也可以说∠1
是∠2的补角,∠2也是∠1的补角.
反之(2)如果∠1与∠2互补,那么∠1+∠2=180°,
∠1=180°-∠2
1
2
【例1】已知∠α=50°17′,求∠α的余角和补角.
解:∠α的余角=90°-50°17'=39°43',
∠α的补角=180°-50°17'=129°43'.
【例题】
〖例2〗.已知一个角的补角等于这个角的余角的3倍,求这个角。
(3)80°的补角是 ,120°的补角是 ;
(4)45°的补角是 ,135°的补角是 ;
50°
40°
25°
55°
100°
60°
135°
45°
(1)40°的余角是 ,50°的余角是 ;
(2)65°的余角是 ,35°的余角是 ;
(5)∠α(α<90°)的余角是 ,
∠α的补角是 .
90°-∠α
180°-∠α
1.填空
【跟踪训练】
2.O是直线AB上的一点,OC是∠AOB的平分线.
看图回答: ①图中互余的角是 ,图中互补的角是 ; ②若∠AOD=53°13′,则∠DOC= ,∠BOD= .
∠AOD与∠DOC
∠AOD与∠DOB、
36°47'
126°47'
C
D
·
O
B
A
∠AOC与∠BOC
1. 直角,钝角有余角吗?
2.一个角的余角一定是锐角吗?举例说明
3.一个角的补角一定是锐角吗?举例说明
4.同角或等角余角相等,为什么
5.同角或等角补角相等,为什么
直角,钝角没有余角
一个角的余角一定是锐角
一个角的补角不一定是锐角
正确
正确
从练习(1)(2)中,同学们能得出什么结论
答:同角(或等角)的余角相等.
(1)判断,当∠1+∠2=90°,∠2+∠3=90°时,∠1=∠3.( )
(2)判断,当∠1+∠2=90°,∠3+∠4=90°,且∠2=∠3时,
则∠1 = ∠4.( )
1
2
3
4
1
2
3
答:同角(或等角)的补角相等.
正确
从练习(3)(4)中,同学们能得出什么结论
正确
(3)判断,当∠1+∠2=180°,∠2+∠3=180°时,∠1=∠3.
( )
2
O
1
3
(4)判断,当∠1+∠2=180°,∠3+∠4=180°,且∠1=∠3时,
则∠2 = ∠4 .( )
O
1
2
3
4
1. 若∠1与∠2互补,∠3+∠2=_180°则∠1与∠3的关系为( )理由是( )
②若∠1=180°-∠2,则∠1与∠2( )
若∠1+∠2=90°;∠3+∠4=90°,且∠1=∠3则∠2与∠4的关系为( )理由是( )
④60°角的余角的补角是 ____
⑤一个角是它的补角的3倍,这个角是 .
随堂练习
2.如图,在三角形ABC中,∠ACB=90,若∠1=∠B,∠A与∠2的大小关系是( )理由是( )
A
B
C
1
2
∠1=∠3
同角的补角相等
互补
∠2=∠4
等角的补角相等
150°
135°
∠A=∠2
等角的余角相等
3.(临沂·中考) 已知一个角的余角等于40°,则这个角的补角等于 ( )
(A)130° (B)140° (C)50° (D)120°
4.(佛山·中考)150°角的补角的余角是( ).
A.30°角 B. 60°角 C. 90°角 D. 150°角
.
A
B
√
╳
╳
5. 判断:
①一个角的余角一定是锐角( )
②一个角的补角一定是钝角( )
③若∠1+∠2+∠3=90°,那么∠1、∠2、∠3互为余角
( )
已知:如图,∠AOB=150°,∠AOC=∠BOD=90°,求∠COD的度数
O
D
C
B
A
1.角的两种特殊关系:
互余、互补
2.角的两个性质:
同角或等角的余角相等
同角或等角的补角相等
3 余角和补角
1.认识角的两种特殊关系:
互余、互补
2.掌握角的两个性质:
同角或等角的余角相等
同角或等角的补角相等
自学课本P152页思考以下问题:
1.互为余角的定义;
2.互为补角的定义;
3.互余,互补是指几个角的关系?
4.互为余角,互为补角的角与角的位置有关吗?它们是否必须有公共顶点,公共边?
5.说说互余,互补的区别和共同之处
6.如何用数学语言表述两个角互余,互补.
30°
150°
·
3
4
定义:
两个角的和等于90°(直角),就说这两个角互为余角,
简称互余;
如果两个角的和等于180°(平角),就说这两个角互为
补角,简称互补.
37°
53°
·
1
2
A
B
C
D
请同学们比较互补与互余的概念,说说它们的区别和
共同之处?
区别:互余是两个角的和是直角,互补是两个角的和
是平角.
相同:(1)互余和互补都是对两个角而言;
(2)不管这两个角在什么位置,只要满足两角和是
90度(180度),它们都互余(补)
(角的数量特点)
1
2
2
1
两个角互余用数学语言表述为:
(1)如果∠1+∠2=90°,则∠1与∠2互余,也可以说∠1是∠2的余角,∠2也是∠1的余角.
反之:(2)如果∠1与∠2互余,那么∠1+∠2=90°,
∠1=90°-∠2
两个角互补用数学语言表述为:
(1)如果∠1+∠2=180°,则∠1与∠2互补,也可以说∠1
是∠2的补角,∠2也是∠1的补角.
反之(2)如果∠1与∠2互补,那么∠1+∠2=180°,
∠1=180°-∠2
1
2
【例1】已知∠α=50°17′,求∠α的余角和补角.
解:∠α的余角=90°-50°17'=39°43',
∠α的补角=180°-50°17'=129°43'.
【例题】
〖例2〗.已知一个角的补角等于这个角的余角的3倍,求这个角。
(3)80°的补角是 ,120°的补角是 ;
(4)45°的补角是 ,135°的补角是 ;
50°
40°
25°
55°
100°
60°
135°
45°
(1)40°的余角是 ,50°的余角是 ;
(2)65°的余角是 ,35°的余角是 ;
(5)∠α(α<90°)的余角是 ,
∠α的补角是 .
90°-∠α
180°-∠α
1.填空
【跟踪训练】
2.O是直线AB上的一点,OC是∠AOB的平分线.
看图回答: ①图中互余的角是 ,图中互补的角是 ; ②若∠AOD=53°13′,则∠DOC= ,∠BOD= .
∠AOD与∠DOC
∠AOD与∠DOB、
36°47'
126°47'
C
D
·
O
B
A
∠AOC与∠BOC
1. 直角,钝角有余角吗?
2.一个角的余角一定是锐角吗?举例说明
3.一个角的补角一定是锐角吗?举例说明
4.同角或等角余角相等,为什么
5.同角或等角补角相等,为什么
直角,钝角没有余角
一个角的余角一定是锐角
一个角的补角不一定是锐角
正确
正确
从练习(1)(2)中,同学们能得出什么结论
答:同角(或等角)的余角相等.
(1)判断,当∠1+∠2=90°,∠2+∠3=90°时,∠1=∠3.( )
(2)判断,当∠1+∠2=90°,∠3+∠4=90°,且∠2=∠3时,
则∠1 = ∠4.( )
1
2
3
4
1
2
3
答:同角(或等角)的补角相等.
正确
从练习(3)(4)中,同学们能得出什么结论
正确
(3)判断,当∠1+∠2=180°,∠2+∠3=180°时,∠1=∠3.
( )
2
O
1
3
(4)判断,当∠1+∠2=180°,∠3+∠4=180°,且∠1=∠3时,
则∠2 = ∠4 .( )
O
1
2
3
4
1. 若∠1与∠2互补,∠3+∠2=_180°则∠1与∠3的关系为( )理由是( )
②若∠1=180°-∠2,则∠1与∠2( )
若∠1+∠2=90°;∠3+∠4=90°,且∠1=∠3则∠2与∠4的关系为( )理由是( )
④60°角的余角的补角是 ____
⑤一个角是它的补角的3倍,这个角是 .
随堂练习
2.如图,在三角形ABC中,∠ACB=90,若∠1=∠B,∠A与∠2的大小关系是( )理由是( )
A
B
C
1
2
∠1=∠3
同角的补角相等
互补
∠2=∠4
等角的补角相等
150°
135°
∠A=∠2
等角的余角相等
3.(临沂·中考) 已知一个角的余角等于40°,则这个角的补角等于 ( )
(A)130° (B)140° (C)50° (D)120°
4.(佛山·中考)150°角的补角的余角是( ).
A.30°角 B. 60°角 C. 90°角 D. 150°角
.
A
B
√
╳
╳
5. 判断:
①一个角的余角一定是锐角( )
②一个角的补角一定是钝角( )
③若∠1+∠2+∠3=90°,那么∠1、∠2、∠3互为余角
( )
已知:如图,∠AOB=150°,∠AOC=∠BOD=90°,求∠COD的度数
O
D
C
B
A
1.角的两种特殊关系:
互余、互补
2.角的两个性质:
同角或等角的余角相等
同角或等角的补角相等
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
