4.5.2 线段的长短比较 课件(共29张PPT)
文档属性
| 名称 | 4.5.2 线段的长短比较 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 08:00:31 | ||
图片预览






文档简介
(共29张PPT)
第4章 图形的初步认识
4.5.2 线段的长短比较
A
B
图1
b
图2
a
图3
O
A
图4
A
B
图5
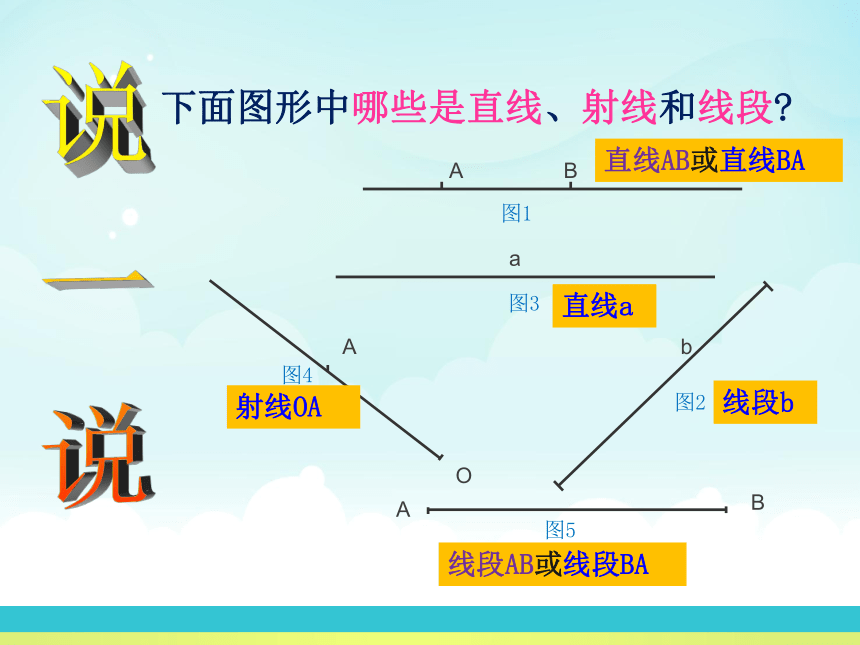
下面图形中哪些是直线、射线和线段
说一说
直线AB或直线BA
线段b
直线a
射线OA
线段AB或线段BA
线段、射线、直线的本质区别
是_____没有端点,_____只有
一个端点,_____有两个端点。
忆一忆
直线
线段
射线
直线的基本事实是:
____________________。
两点确定一条直线
线段、射线、直线中____可以
度量长度,所以只有____才可
以比较长短。
线段
线段
线段的基本事实是:
____________________。
两点之间,线段最短
1
创设情境
还记得你和同学是怎样比较个子高矮的吗 请说出你的想法
小明
小华
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
小明
小华
线段长短的比较
生活中的长短的比较
怎样比较两个同学的高矮
叠合法
度量法
2
讲授新课
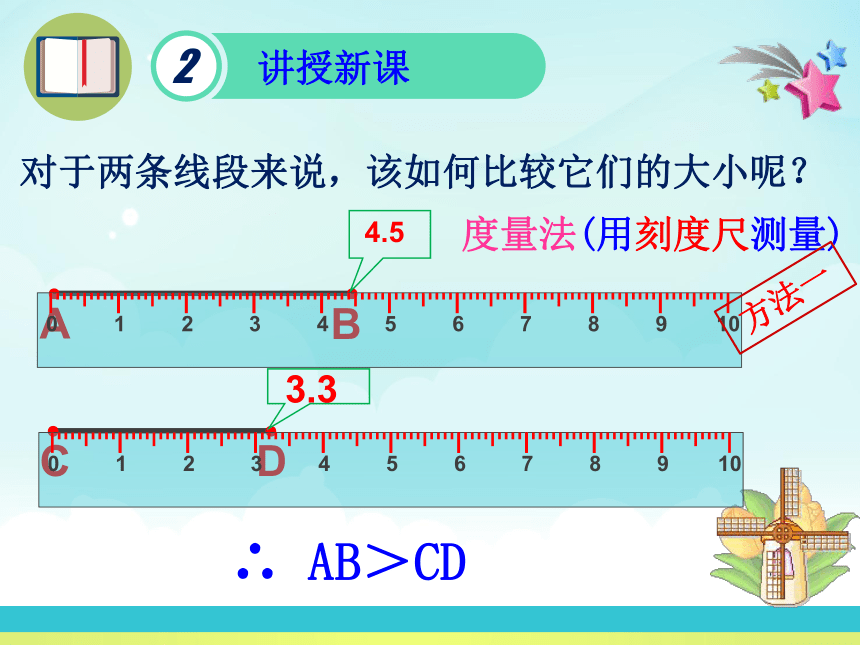
对于两条线段来说,该如何比较它们的大小呢?
●
●
A
B
●
●
C
D
4.5
1
3
2
8
7
4
9
6
5
0
10
3.3
1
3
2
8
7
4
9
6
5
0
10
∴ AB>CD
度量法(用刻度尺测量)
方法一
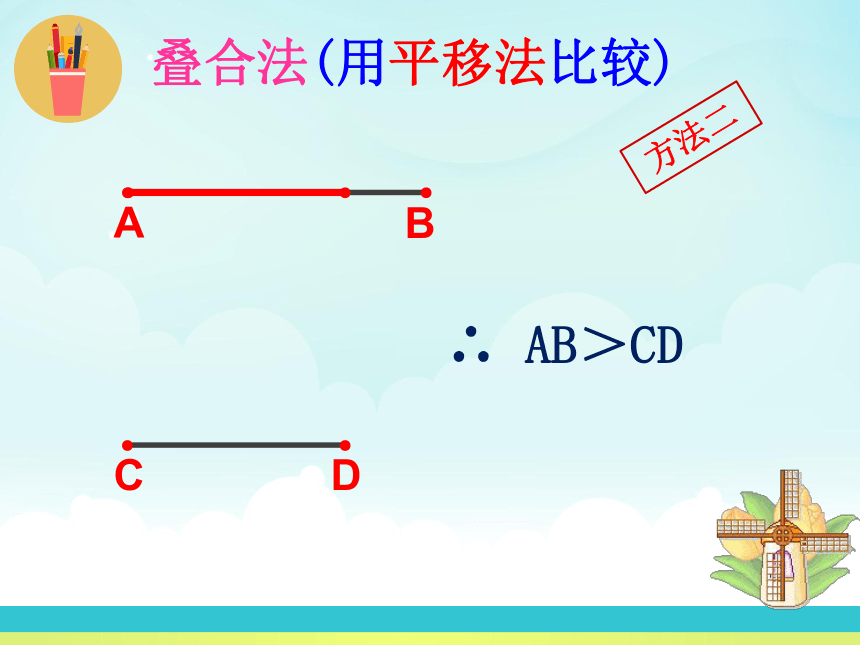
叠合法(用平移法比较)
●
●
A
B
●
●
C
D
●
●
∴ AB>CD
方法二
D
C
(1)如果点B在线段CD上,记作AB(2)如果点B在线段CD的延长线上, 记作AB>CD
(3)如果点B与点D重合,记作AB=CD
叠合法
注意:起点对齐,看终点。
A
B
A
B
A
A
B
A
D
C
A
B
C
D
1.度量法
2.叠合法
方法归纳
注意:
用度量法是从数的方面去比较大小,而叠合法是从形的方面去比较大小。
要比较两条线段的长短,你有几种方法
起点对齐
看终点
课本P143页练习第3题:
(1)
a
b
(3)
(2)
a
b
a
b
观察下列三组图形,分别比较线段a、b的长短。再用刻度尺量一下,看看你的观察结果是否正确。
归纳:比较线段长短的两种方法:
1.度量法——从“数值”的角度比较
2.叠合法——从“形”的角度比较
做一做
如图,MN为已知线段,你能用直尺和圆规准确地画一条与MN相等的线段吗
M N
3
深入探究
M N
1
3
2
8
7
4
9
6
5
0
10
方法一:用刻度尺画
M N
1
3
2
8
7
4
9
6
5
0
10
∴ 线段MN即为所求。
M N
A B
C
1、画射线AB ;
2、用圆规量出线段MN的长;
3、在射线AB上截取AC=MN,线段AC就是所要画的线段。
方法二:用圆规截取
∴ 线段AC即为所求。
1.已知线段MN,用直尺和圆规画一条线段OA,使它等于已知线段MN。
M
尺规作图注意事项:
1.作图语言要规范,要
说明作图结果;
2.保留作图痕迹。
O
P
∴ 线段OA即为所求。
画一画
A
直尺只用来画线,不用来量距离;
N
a
2.你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍。
O
P
B
∴ 线段OB即为所求求做的线段c。
画一画
A
OA+AB= ( )
OA=( ) -AB
AB=OB- ( )
根据图形回答:
OB
OB
AB
结论:
线段类同于数,彼此间可相互加减。
如图,填空:
A
B
C
D
AB+BC= ( )
AC
AD - CD=( )
AC
BC=( ) - CD
BD
AD=( ) + ( ) + ( )
AB
BC
CD
线段的和、差
按图填空
●
●
●
●
●
A
C
E
D
B
1.AB=( )+( )+( )+( )
2.AE=( )-( )-( )
3.AC+CD=( )- BD
4.CE+EB-ED=( )+( )
5.AE+( )=( )-DB
=AC+( )=AD
DB
AB
ED
DB
AB
CE
ED
AB
CD
AC
CE
DB
ED
课本P143页练习第1题
例1.已知:直线l上有A、B、C三点,且线段AB=8,
线段BC=5,求线段AC的长。
解: 分两种情况
1).当C在B的右边时,如图
2).当C在B的左边时,如图
AC=AB+BC
=8+5
=13
AC=AB-BC
=8-5
=3
A
B
C
A
B
C
试一试:
已知:直线m上有A、B、C三点,且线段AB=10cm,线段BC=4cm,求线段AC的长。
l
l
4
例题讲解
∴ 综上所述,线段AC的长为13或3。
把一条线段分成两条相等线段的点,叫做这条线段的中点。ABC如图, C是线段AB上一点,且AC=CB如图,点C是线段AB的中点,如果AB=4,那么线段AC,CB有多长呢?线段中点那么,点C是线段AB的中点。∵点C是线段AB的中点中点的性质几何语言例2:如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
∴AC=CB=
A
D
C
B
中点应用
解:∵点C是线段AB的中点
∵点D是线段BC的中点
∴CD=
∴AD=
AC+CD
思考:
此题还有没有其他解法?
练习:
1.如图,已知点C是线段AB的中点,点D是线段AC的中点,完成下列填空:
(1)AB= BC ,BC= AD
(2)BD= AD
A
B
C
D
2
2
3
2.在下图中,点C是线段AB的中点。如果AB=4cm,那么AC= ,BC= 。
2cm
4cm
A
B
C
课本P143页练习第2题
一、学习了怎样比较线段的长短。
1、度量法:
2、叠合法:起点对齐,看终点。
谈谈收获吧
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差。
三、知道线段中点的定义,会用几何符号表示线段的中点。
一看起点,二看方向,三看落点。
作业
3.课本P144页作业第3,4,5题
2.已知如图,点C是线段AD的中点,AC=4cm,BD=2cm,则
AB的长度为多少?
A
D
C
B
1.已知:直线m上有A、B、C三点,且线段AB=18cm,线段BC=14cm,求线段AC的长。(分情况计算)
谢谢欣赏
THANK YOU FOR LISTENING
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
1. ①线段AB=6厘米,点C在线段AB上,且BC=3厘米,则线段AC的长为( )
A. 3厘米 B. 9厘米
C. 3厘米或9厘米 D. 无法确定
②线段AB=6厘米,点C在直线AB上,且BC=3厘米,则线段AC的长为( )
A. 3厘米 B. 9厘米
C. 3厘米或9厘米 D.无法确定
A
C
基 础 过 关
2. 如图,B、C为线段AD上的两点,点C为线段AD的中点,AC=5cm,BD=6cm,求线段AB的长度?
A
C
B
D
解:∵ AC=5cm,C为线段AD的中点
∴ AD=2AC=10cm
∵ BD=6cm
∴ AB=AD-BD=10-4=4cm
答:线段AB的长为4cm。
基 础 过 关
3.在直线上顺次取出A、B、C三点使AB=4cm,
BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:∵ AB=4cm BC=3cm
∴ AC=AB+BC=7cm
∵ 点O是线段AC的中点
∴OC= AC = 3.5cm
∴OB= OC-BC = 3.5-3 = 0.5(cm)
答:线段OB的长为0.5cm。
基 础 过 关
第4章 图形的初步认识
4.5.2 线段的长短比较
A
B
图1
b
图2
a
图3
O
A
图4
A
B
图5
下面图形中哪些是直线、射线和线段
说一说
直线AB或直线BA
线段b
直线a
射线OA
线段AB或线段BA
线段、射线、直线的本质区别
是_____没有端点,_____只有
一个端点,_____有两个端点。
忆一忆
直线
线段
射线
直线的基本事实是:
____________________。
两点确定一条直线
线段、射线、直线中____可以
度量长度,所以只有____才可
以比较长短。
线段
线段
线段的基本事实是:
____________________。
两点之间,线段最短
1
创设情境
还记得你和同学是怎样比较个子高矮的吗 请说出你的想法
小明
小华
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
小明
小华
线段长短的比较
生活中的长短的比较
怎样比较两个同学的高矮
叠合法
度量法
2
讲授新课
对于两条线段来说,该如何比较它们的大小呢?
●
●
A
B
●
●
C
D
4.5
1
3
2
8
7
4
9
6
5
0
10
3.3
1
3
2
8
7
4
9
6
5
0
10
∴ AB>CD
度量法(用刻度尺测量)
方法一
叠合法(用平移法比较)
●
●
A
B
●
●
C
D
●
●
∴ AB>CD
方法二
D
C
(1)如果点B在线段CD上,记作AB
(3)如果点B与点D重合,记作AB=CD
叠合法
注意:起点对齐,看终点。
A
B
A
B
A
A
B
A
D
C
A
B
C
D
1.度量法
2.叠合法
方法归纳
注意:
用度量法是从数的方面去比较大小,而叠合法是从形的方面去比较大小。
要比较两条线段的长短,你有几种方法
起点对齐
看终点
课本P143页练习第3题:
(1)
a
b
(3)
(2)
a
b
a
b
观察下列三组图形,分别比较线段a、b的长短。再用刻度尺量一下,看看你的观察结果是否正确。
归纳:比较线段长短的两种方法:
1.度量法——从“数值”的角度比较
2.叠合法——从“形”的角度比较
做一做
如图,MN为已知线段,你能用直尺和圆规准确地画一条与MN相等的线段吗
M N
3
深入探究
M N
1
3
2
8
7
4
9
6
5
0
10
方法一:用刻度尺画
M N
1
3
2
8
7
4
9
6
5
0
10
∴ 线段MN即为所求。
M N
A B
C
1、画射线AB ;
2、用圆规量出线段MN的长;
3、在射线AB上截取AC=MN,线段AC就是所要画的线段。
方法二:用圆规截取
∴ 线段AC即为所求。
1.已知线段MN,用直尺和圆规画一条线段OA,使它等于已知线段MN。
M
尺规作图注意事项:
1.作图语言要规范,要
说明作图结果;
2.保留作图痕迹。
O
P
∴ 线段OA即为所求。
画一画
A
直尺只用来画线,不用来量距离;
N
a
2.你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍。
O
P
B
∴ 线段OB即为所求求做的线段c。
画一画
A
OA+AB= ( )
OA=( ) -AB
AB=OB- ( )
根据图形回答:
OB
OB
AB
结论:
线段类同于数,彼此间可相互加减。
如图,填空:
A
B
C
D
AB+BC= ( )
AC
AD - CD=( )
AC
BC=( ) - CD
BD
AD=( ) + ( ) + ( )
AB
BC
CD
线段的和、差
按图填空
●
●
●
●
●
A
C
E
D
B
1.AB=( )+( )+( )+( )
2.AE=( )-( )-( )
3.AC+CD=( )- BD
4.CE+EB-ED=( )+( )
5.AE+( )=( )-DB
=AC+( )=AD
DB
AB
ED
DB
AB
CE
ED
AB
CD
AC
CE
DB
ED
课本P143页练习第1题
例1.已知:直线l上有A、B、C三点,且线段AB=8,
线段BC=5,求线段AC的长。
解: 分两种情况
1).当C在B的右边时,如图
2).当C在B的左边时,如图
AC=AB+BC
=8+5
=13
AC=AB-BC
=8-5
=3
A
B
C
A
B
C
试一试:
已知:直线m上有A、B、C三点,且线段AB=10cm,线段BC=4cm,求线段AC的长。
l
l
4
例题讲解
∴ 综上所述,线段AC的长为13或3。
把一条线段分成两条相等线段的点,叫做这条线段的中点。ABC如图, C是线段AB上一点,且AC=CB如图,点C是线段AB的中点,如果AB=4,那么线段AC,CB有多长呢?线段中点那么,点C是线段AB的中点。∵点C是线段AB的中点中点的性质几何语言例2:如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
∴AC=CB=
A
D
C
B
中点应用
解:∵点C是线段AB的中点
∵点D是线段BC的中点
∴CD=
∴AD=
AC+CD
思考:
此题还有没有其他解法?
练习:
1.如图,已知点C是线段AB的中点,点D是线段AC的中点,完成下列填空:
(1)AB= BC ,BC= AD
(2)BD= AD
A
B
C
D
2
2
3
2.在下图中,点C是线段AB的中点。如果AB=4cm,那么AC= ,BC= 。
2cm
4cm
A
B
C
课本P143页练习第2题
一、学习了怎样比较线段的长短。
1、度量法:
2、叠合法:起点对齐,看终点。
谈谈收获吧
二、尺规作图
1、用尺规法画一条线段等于已知线段;
2、用尺规法画已知线段的和与差。
三、知道线段中点的定义,会用几何符号表示线段的中点。
一看起点,二看方向,三看落点。
作业
3.课本P144页作业第3,4,5题
2.已知如图,点C是线段AD的中点,AC=4cm,BD=2cm,则
AB的长度为多少?
A
D
C
B
1.已知:直线m上有A、B、C三点,且线段AB=18cm,线段BC=14cm,求线段AC的长。(分情况计算)
谢谢欣赏
THANK YOU FOR LISTENING
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
1. ①线段AB=6厘米,点C在线段AB上,且BC=3厘米,则线段AC的长为( )
A. 3厘米 B. 9厘米
C. 3厘米或9厘米 D. 无法确定
②线段AB=6厘米,点C在直线AB上,且BC=3厘米,则线段AC的长为( )
A. 3厘米 B. 9厘米
C. 3厘米或9厘米 D.无法确定
A
C
基 础 过 关
2. 如图,B、C为线段AD上的两点,点C为线段AD的中点,AC=5cm,BD=6cm,求线段AB的长度?
A
C
B
D
解:∵ AC=5cm,C为线段AD的中点
∴ AD=2AC=10cm
∵ BD=6cm
∴ AB=AD-BD=10-4=4cm
答:线段AB的长为4cm。
基 础 过 关
3.在直线上顺次取出A、B、C三点使AB=4cm,
BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:∵ AB=4cm BC=3cm
∴ AC=AB+BC=7cm
∵ 点O是线段AC的中点
∴OC= AC = 3.5cm
∴OB= OC-BC = 3.5-3 = 0.5(cm)
答:线段OB的长为0.5cm。
基 础 过 关
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
