5.2.2 平行线的判定 课件(共17张PPT)
文档属性
| 名称 | 5.2.2 平行线的判定 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 08:22:19 | ||
图片预览




文档简介
(共17张PPT)
*
*
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
*
一.在同一平面内,两条直线之间有几种位置关系呢?
特殊相交:垂直
1.相交
2.平行
回 顾:
二.判定两条直线平行的方法有哪些
1.根据定义:在同一平面内,不相交的两条直线叫平行线。
同学们可以想一想:
除以上两种方法以外,是否还有其它方法呢?
2.平行线公理推论:如果两条直线都和第三条直线平行,那么这两条直线也平行。
·
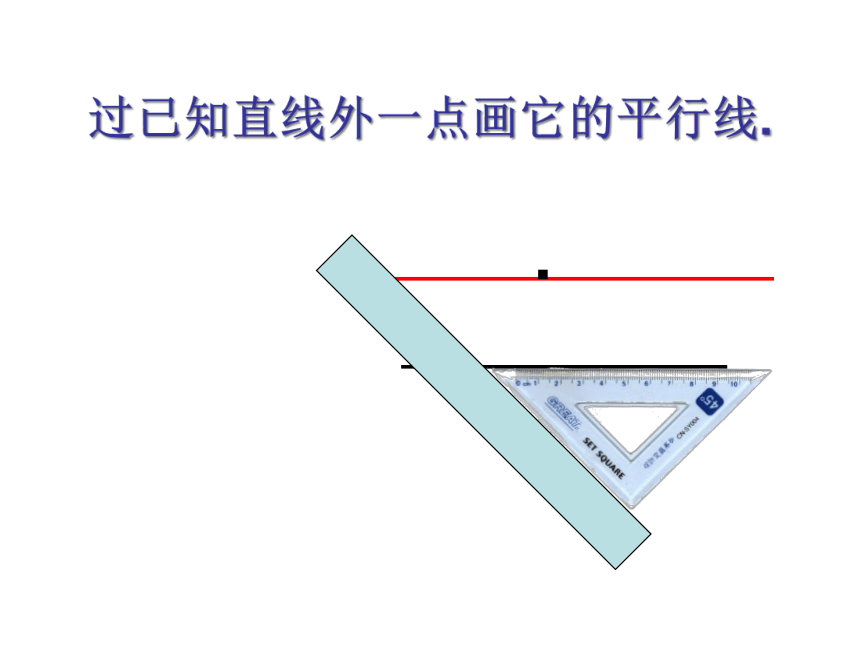
过已知直线外一点画它的平行线.
1
A
2
1
2
B
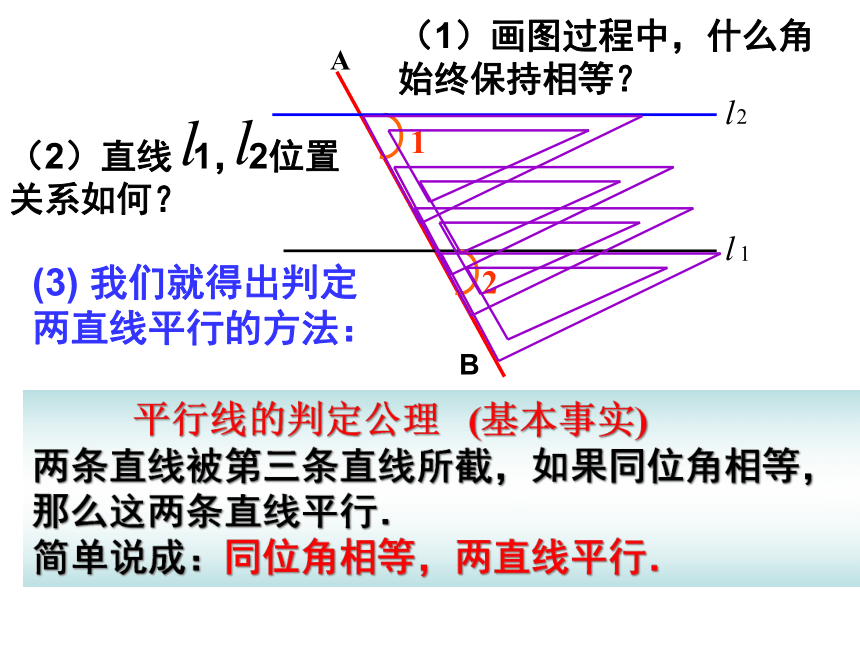
(1)画图过程中,什么角始终保持相等?
(2)直线 1,2位置
关系如何?
(3) 我们就得出判定两直线平行的方法:
平行线的判定公理 (基本事实)
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行.
简单说成:同位角相等,两直线平行.
*
画图并回答问题:
过直线l外一点P画直线l 的平行线,
1.三角尺紧靠直尺的边和直线l 所成的角在平移前的位置和
平移后的位置构成了一对_ _____角,其大小_ _____。
2.只要保持___ __相等,画出的直线就平行于已知直线。
3.怎样才能构成同位角?
4.由上面的画图与问题,你能否用一句话来概括?
同位
始终不变
同位角
两条直线被第三条直线所截
同位角相等,二直线平行
*
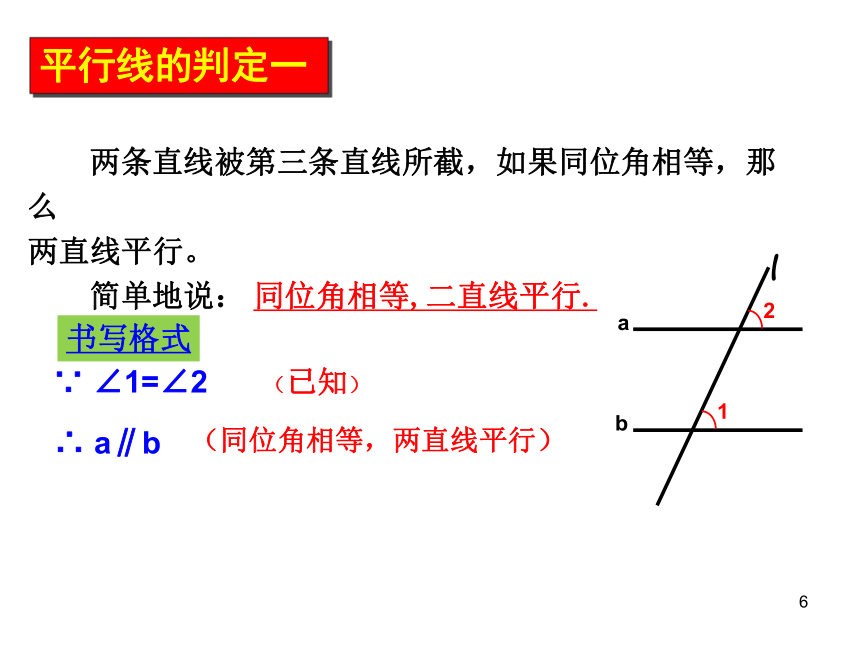
平行线的判定一
两条直线被第三条直线所截,如果同位角相等,那么
两直线平行。
简单地说: 同位角相等,二直线平行.
∵ ∠1=∠2
∴ a∥b
书写格式
a
b
l
2
1
(已知)
(同位角相等,两直线平行)
*
4
1
2
3
A
B
C
E
F
D
5
H
G
如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
想一想
*
大家来探索!
①如图:如果∠1=∠2,那么a与b平行吗?
a
b
l
1
2
3
∵ ∠1=∠2
∠3=∠2
∴ ∠1=∠3
∴ a∥b
(已知)
(同位角相等,两直线平行)
(对顶角相等)
(等量代换)
平行线的判定二
两条直线被第三条直线所截,如果内错角相等,那么两直线平行。
简单地说:内错角相等,二直线平行.
∵ ∠1=∠2
∴ a∥b
书写格式
(已知)
(内错角相等,两直线平行)
*
例1:如图,直线a、b 被直线l所截,已知∠1=115°,
∠2=115°,直线a、b 平行吗 为什么
a
b
l
1
2
解:a与b平行
理由如下:
∵∠1= 115°,∠2=115°
∴∠1= ∠2
∴a//b
(已知)
(等量代换)
(内错角相等,两直线平行)
100°
1.如图,∠1=100°,∠2=100°,a∥b吗?为什么
2.如图,若∠3=100°,∠4=__时,a∥b。
1
2
a
b
3
4
a
b
练习:
∠1与∠2不是内错角
*
继续探索!
② 如图: 如果∠1+∠2=180o, 那么a与b平行吗?
a
b
l
1
2
3
∵ ∠1+∠2=180o
∴ ∠2=∠3
∴ a∥b
(已知)
(同位角相等,两直线平行)
(邻补角互补)
(等量代换)
∠1+∠3=180o
(同角的补角相等)
平行线的判定三
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。
简单地说:同旁内角互补,二直线平行.
∵ ∠1 +∠2=180o
∴ a∥b
书写格式
(已知)
(同旁内角互补,两直线平行)
*
A
C
1
4
2
3
5
8
6
7
B
D
练习:
① ∵ ∠2 =___(已知)
∴ ___∥___( )
② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )
③∵ ∠4 +___=180o(已知)
∴ ___∥___( )
∠6
AB
CD
AB
CD
AB
CD
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
∠5
*
例2.如图,直线a、b被直线c所截,若∠1+∠2=180°,那么直线a与直线b平行吗?为什么?
解:∵∠1+∠2=180°
∠1+∠3=180°
∴∠2=∠3
∴a//b
(已知)
(互补的定义)
(同角的补角相等)
(内错角相等,两直线平行)
例3.已知:∠1=75o ,∠2 =105o.问:AB与CD平行吗? 为什么?
A
C
1
4
2
3
B
D
5
解:∵∠1+∠3=180°
∠1=75°
∴∠3= 105°
∵∠2=105°
∴∠3=∠2
∴a//b
(已知)
(等式性质)
(已知)
(等量代换)
(同位角相等,两直线平行)
(邻补角定义)
*
例4:如图,在四边形ABCD中,已知∠B=60°,∠C=120°.
AB与CD平行吗?AD与BC平行吗?
A
B
C
D
解:直线AB与CD平行.
理由如下:
∵∠B=60°,∠C=120°( )
∴∠B+C=180°( )
∴AB//CD( )
根据题目条件无法判定AD与BC平行。
已知
等式的性质
同旁内角互补,两直线平行
*
做一做.
1
3
5
4
2
C
F
E
A
D
B
① ∵ ∠1 =_____(已知)
∴ AB∥CE9( )
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )
∠3
∠3
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
课本P174页练习第1,2题
*
思考:如图,在同一平面内,直线CD、EF均与直线 AB垂
直,D、F为垂足,试判断CD与EF是否平行。
A
B
C
D
E
F
1
2
解:∵CD⊥AB
EF⊥AB
∴∠1= ∠2=90°
∴CD∥EF
由此可以得出什么结论?
结论:
在同一平面内,垂直于同一条直线的两条直线平行.
(已知)
(已知)
(垂直定义)
(同位角相等,两直线平行)
*
小结:识别平行线的方法:
1、平行线的定义:在同一平面内不相交得两条直线。
3、同位角相等,两直线平行;
4、内错角相等,两直线平行;
5、同旁内角互补,两直线平行;
6、垂直于同一条直线的两条直线互相平行;
2、平行于同一条直线的两条直线互相平行。
*
作 业
1.如图1,∠C=57°,当∠ABE= 时,就能使BE∥CD.
2.如图2 , ∠1=120°,∠2=60°.问a与b平行吗
图1
图2
A
B
E
C
D
1
2
a
b
3
c
3.课本P179页习题第1,2,3题
*
*
义务教育课程标准试验教科书 七年级 上册
华东师范大学出版社
*
一.在同一平面内,两条直线之间有几种位置关系呢?
特殊相交:垂直
1.相交
2.平行
回 顾:
二.判定两条直线平行的方法有哪些
1.根据定义:在同一平面内,不相交的两条直线叫平行线。
同学们可以想一想:
除以上两种方法以外,是否还有其它方法呢?
2.平行线公理推论:如果两条直线都和第三条直线平行,那么这两条直线也平行。
·
过已知直线外一点画它的平行线.
1
A
2
1
2
B
(1)画图过程中,什么角始终保持相等?
(2)直线 1,2位置
关系如何?
(3) 我们就得出判定两直线平行的方法:
平行线的判定公理 (基本事实)
两条直线被第三条直线所截,如果同位角相等,
那么这两条直线平行.
简单说成:同位角相等,两直线平行.
*
画图并回答问题:
过直线l外一点P画直线l 的平行线,
1.三角尺紧靠直尺的边和直线l 所成的角在平移前的位置和
平移后的位置构成了一对_ _____角,其大小_ _____。
2.只要保持___ __相等,画出的直线就平行于已知直线。
3.怎样才能构成同位角?
4.由上面的画图与问题,你能否用一句话来概括?
同位
始终不变
同位角
两条直线被第三条直线所截
同位角相等,二直线平行
*
平行线的判定一
两条直线被第三条直线所截,如果同位角相等,那么
两直线平行。
简单地说: 同位角相等,二直线平行.
∵ ∠1=∠2
∴ a∥b
书写格式
a
b
l
2
1
(已知)
(同位角相等,两直线平行)
*
4
1
2
3
A
B
C
E
F
D
5
H
G
如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
想一想
*
大家来探索!
①如图:如果∠1=∠2,那么a与b平行吗?
a
b
l
1
2
3
∵ ∠1=∠2
∠3=∠2
∴ ∠1=∠3
∴ a∥b
(已知)
(同位角相等,两直线平行)
(对顶角相等)
(等量代换)
平行线的判定二
两条直线被第三条直线所截,如果内错角相等,那么两直线平行。
简单地说:内错角相等,二直线平行.
∵ ∠1=∠2
∴ a∥b
书写格式
(已知)
(内错角相等,两直线平行)
*
例1:如图,直线a、b 被直线l所截,已知∠1=115°,
∠2=115°,直线a、b 平行吗 为什么
a
b
l
1
2
解:a与b平行
理由如下:
∵∠1= 115°,∠2=115°
∴∠1= ∠2
∴a//b
(已知)
(等量代换)
(内错角相等,两直线平行)
100°
1.如图,∠1=100°,∠2=100°,a∥b吗?为什么
2.如图,若∠3=100°,∠4=__时,a∥b。
1
2
a
b
3
4
a
b
练习:
∠1与∠2不是内错角
*
继续探索!
② 如图: 如果∠1+∠2=180o, 那么a与b平行吗?
a
b
l
1
2
3
∵ ∠1+∠2=180o
∴ ∠2=∠3
∴ a∥b
(已知)
(同位角相等,两直线平行)
(邻补角互补)
(等量代换)
∠1+∠3=180o
(同角的补角相等)
平行线的判定三
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。
简单地说:同旁内角互补,二直线平行.
∵ ∠1 +∠2=180o
∴ a∥b
书写格式
(已知)
(同旁内角互补,两直线平行)
*
A
C
1
4
2
3
5
8
6
7
B
D
练习:
① ∵ ∠2 =___(已知)
∴ ___∥___( )
② ∵ ∠3 = ∠5(已知)
∴ ___∥___( )
③∵ ∠4 +___=180o(已知)
∴ ___∥___( )
∠6
AB
CD
AB
CD
AB
CD
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
∠5
*
例2.如图,直线a、b被直线c所截,若∠1+∠2=180°,那么直线a与直线b平行吗?为什么?
解:∵∠1+∠2=180°
∠1+∠3=180°
∴∠2=∠3
∴a//b
(已知)
(互补的定义)
(同角的补角相等)
(内错角相等,两直线平行)
例3.已知:∠1=75o ,∠2 =105o.问:AB与CD平行吗? 为什么?
A
C
1
4
2
3
B
D
5
解:∵∠1+∠3=180°
∠1=75°
∴∠3= 105°
∵∠2=105°
∴∠3=∠2
∴a//b
(已知)
(等式性质)
(已知)
(等量代换)
(同位角相等,两直线平行)
(邻补角定义)
*
例4:如图,在四边形ABCD中,已知∠B=60°,∠C=120°.
AB与CD平行吗?AD与BC平行吗?
A
B
C
D
解:直线AB与CD平行.
理由如下:
∵∠B=60°,∠C=120°( )
∴∠B+C=180°( )
∴AB//CD( )
根据题目条件无法判定AD与BC平行。
已知
等式的性质
同旁内角互补,两直线平行
*
做一做.
1
3
5
4
2
C
F
E
A
D
B
① ∵ ∠1 =_____(已知)
∴ AB∥CE9( )
② ∵ ∠1 +_____=180o(已知)
∴ CD∥BF( )
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____( )
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )
∠3
∠3
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
课本P174页练习第1,2题
*
思考:如图,在同一平面内,直线CD、EF均与直线 AB垂
直,D、F为垂足,试判断CD与EF是否平行。
A
B
C
D
E
F
1
2
解:∵CD⊥AB
EF⊥AB
∴∠1= ∠2=90°
∴CD∥EF
由此可以得出什么结论?
结论:
在同一平面内,垂直于同一条直线的两条直线平行.
(已知)
(已知)
(垂直定义)
(同位角相等,两直线平行)
*
小结:识别平行线的方法:
1、平行线的定义:在同一平面内不相交得两条直线。
3、同位角相等,两直线平行;
4、内错角相等,两直线平行;
5、同旁内角互补,两直线平行;
6、垂直于同一条直线的两条直线互相平行;
2、平行于同一条直线的两条直线互相平行。
*
作 业
1.如图1,∠C=57°,当∠ABE= 时,就能使BE∥CD.
2.如图2 , ∠1=120°,∠2=60°.问a与b平行吗
图1
图2
A
B
E
C
D
1
2
a
b
3
c
3.课本P179页习题第1,2,3题
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
