第5章 相交线与平行线复习 课件(共29张PPT)
文档属性
| 名称 | 第5章 相交线与平行线复习 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 300.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-25 08:19:58 | ||
图片预览






文档简介
(共29张PPT)
相交线与平行线
(复习课)
平昌**中学初一年级
年 月 日
知识回顾
A
B
C
D
1
2
3
4
两直线相交 邻补角 对顶角
分类
判定方法(特点)
性质
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
1、顶点相同,
2、有一条公共边,另一边互为反向延线
1、顶点相同,
2、角的两边互为反向延长线
邻补角互补
对顶角相等
相交线
A
B
C
D
C
D
1
O
垂直
判定
性质
两条直线相交时四个交角中一个角是直角
几何语言:∵∠1=90。 ∴AB⊥CD
若直线AB与CD垂直,垂足为O,那么,∠1=90°
几何语言:∵AB⊥CD ∴ ∠1=90。
两直线垂直
A
B
C
D
1
2
3
4
C
D
E
F
1
2
3
4
5
6
7
8
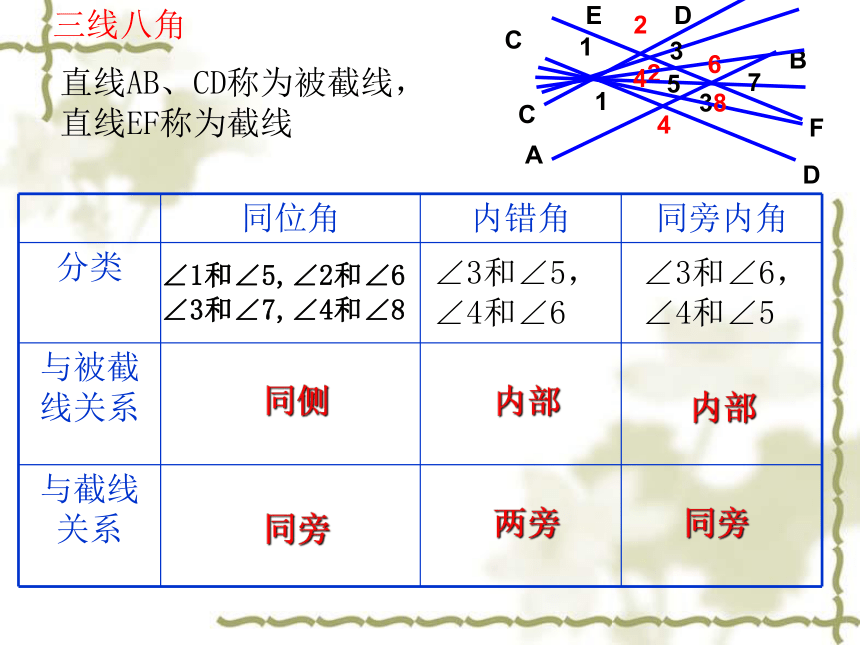
直线AB、CD称为被截线,直线EF称为截线
同位角 内错角 同旁内角
分类
与被截线关系
与截线关系
∠1和∠5,∠2和∠6 ∠3和∠7,∠4和∠8
∠3和∠5,∠4和∠6
∠3和∠6,∠4和∠5
同侧
同旁
内部
同旁
两旁
内部
三线八角
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角 内错角 同旁内角
判定方法
性质
同位角相等,两直线平行
∵∠1=∠5 ∴AB∥CD
内错角相等,两直线平行
∵∠3= ∠ 5 ∴AB∥CD
∵∠3+∠6=180 ° ∴AB∥CD
同旁内角互补,两直线平行
两直线平行,同位角相等
∵AB∥CD ∴ ∠1=∠5
两直线平行,内错角相等
两直线平行, 同旁内角互补
∵ AB∥CD ∴ ∠3= ∠5
∵ AB∥CD ∴∠3+∠6=180 °
平行线
知识应用
E
D
C
B
A
(已知)
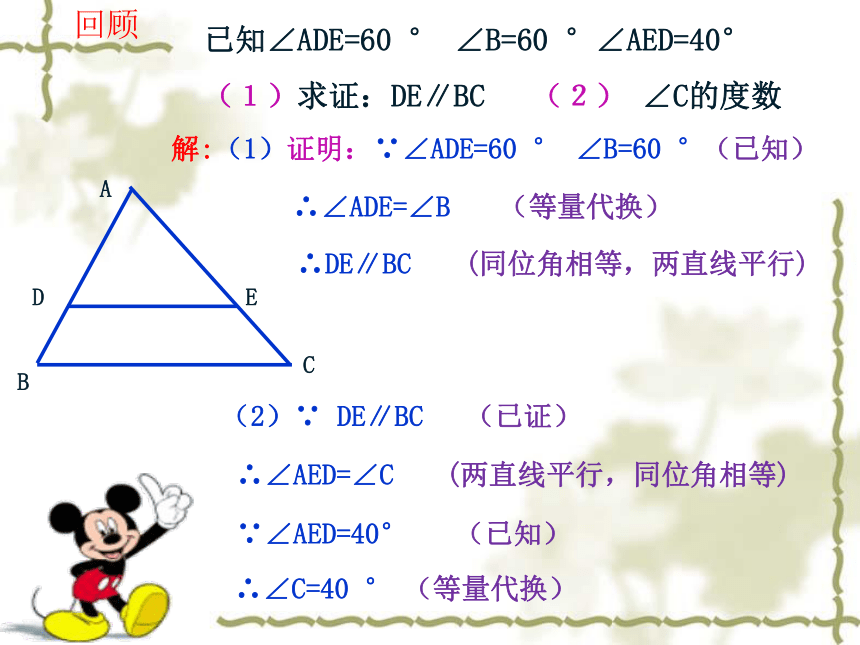
解:(1)证明:∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
已知∠ADE=60 ° ∠B=60 °∠AED=40°
(1)求证:DE∥BC (2) ∠C的度数
回顾
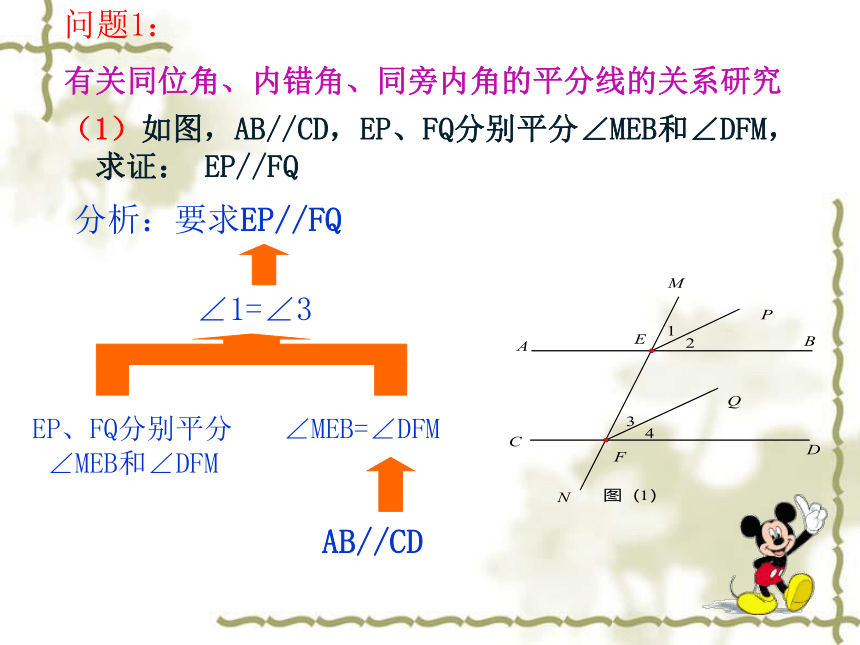
有关同位角、内错角、同旁内角的平分线的关系研究
(1)如图,AB//CD,EP、FQ分别平分∠MEB和∠DFM,求证: EP//FQ
EP、FQ分别平分∠MEB和∠DFM
∠MEB=∠DFM
分析:要求EP//FQ
∠1=∠3
AB//CD
问题1:
(2)如图,AB//CD,EP、FQ分别平分∠AEN和∠DFM,问直线EP与FQ存在什么位置关系?说明你的理由
解:∵ AB//CD( )
∴ ∠AEN=∠DFM ( )
∵ EP、FQ分别平分∠AEN和∠DFM ( )
∴ ∠1=∠ 3( )
∴ EP // FQ( )
已知
两直线平行,内错角相等
已知
角平分线定义
等量代换
内错角相等,两直线平行
∴ ∠1= ∠AEN , ∠ 3= ∠DFM ( )
(3)如图,AB//CD,EQ、FQ分别平分∠BEN和∠DFM,问直线EQ与FQ存在什么位置关系?说明理由
解:∵ AB//CD( )
已知
∴ ∠BEN+∠DFM=180。( )
两直线平行,同旁内角互补
∵ EQ、FQ分别平分∠BEN和∠DFM ( )
已知
角平分线定义
等量代换
∴ ∠ Q=180。-(∠1+∠ 3 )=90。( )
三角形内角和180。
∴ ∠1= ∠BEN , ∠ 3= ∠DFM ( )
∴ ∠1+∠ 3= (∠BEN+∠DFM)=90。( )
∴ EQ ⊥ FQ( )
垂直定义
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
图(1)
F
解:过点P作直线PF平行直线AB
1
2
∵AB∥CD ∴ AB∥CD ∥PF
∴∠A+∠1=180。 ∠2+∠C=180 。 ∴∠A+∠1+ ∠2+∠C =360 。
∵∠APC=∠1 + ∠2 ∴∠A+ ∠APC +∠C =360 。
探索发现:
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明。
图(2)
F
解:过点P作直线PF平行直线AB
∵AB∥CD, ∴ AB∥CD ∥PF
∴∠A=∠1,∠2=∠C
∵∠APC=∠1 + ∠2 ∴ ∠APC =∠A + ∠C
1
2
探索发现:
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明。
图(3)
F
图(4)
F
∠A= ∠P +∠C
∠C= ∠P +∠A
探索发现:
A
B
C
D
E
M
N
P
Q
T
小明现在在做一个工艺插件如图3,遇到一个问题,需要大家帮忙,小明已经量得插件的∠D=60 ,∠E= 122 ,要使∠B为多少度时,AB∥CD。
图3
A
B
C
D
E
F
F
练习
有一个与地面成30°角的斜坡,如图②,现要在斜坡上竖一电线杆,当电线杆与斜坡成的∠ 1= °时,电线杆与地面垂直。
1
图②
30°
练习
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结——
例1:如图,三条直线AB,CD,EF相交于O,且CD⊥EF,∠AOE=70 ,若OG平分∠BOF。
求:∠DOG的度数。
典型例题
解:∵ CD⊥EF(已知)
∴ ∠DOF=90 (垂直的定义)
∵ ∠AOE=70 (已知)
∴ ∠BOF=∠AOE=70 (对顶角相等)
∵ OG平分∠BOF,(已知)
∴ ∠FOG= ∠BOF=35 (角的平分线定义)
∴ ∠DOG=∠DOF-∠FOG
=90 -35 =55
例2:如图所示,直线a、b被c、d所截,且c⊥a,c⊥b.∠1与∠2的相等吗?说明理由。
典型例题
解:∠1与∠2 的度数相等。理由如下:
∵ c⊥a c⊥b(已知)
∴ ∠3=∠4=90 (垂直的定义)
∴ a//b(同位角相等,两直线平行)
∴ ∠5=∠2(两直线平行,同位角相等)
∵ ∠5=∠1(对顶角相等)
∴ ∠2=∠1(等量代换)
d
c
a
b
C
∟
理由:垂线段最短
例3:如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
典型例题
∠1和∠2不是同位角,
练习1:如图中的∠1和∠2是同位角吗 为什么
1
2
1
2
因为∠1和∠2无一边共线。
∠1和∠2是同位角,
因为∠1和∠2有一边共线、同向且不共定点。
随堂练习
A
C
B
D
E
1
2
答:∠EAC
答:∠DAB
答:∠BAC ∠BAE ∠2
2)∠1与哪个角是同旁内角?
3)∠2与哪个角是内错角
1)∠1与哪个角是内错角?
练习2:如图,回答一下问题:
随堂练习
证明: ∵ ∠DAC= ∠ACB (已知)
A
B
C
D
E
F
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
练习3:已知 ∠DAC= ∠ACB, ∠D+∠DFE=180°,
求证:EF//BC
随堂练习
证明:∵∠1+∠2=180°(已知)
4
1
2
3
A
B
C
E
F
D
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
∴∠3+∠4=180°
(等量代换)
∴ AB//CD
练习4:如图 已知:∠1+∠2=180°,
求证:AB∥CD。
随堂练习
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴ AB ∥ CD
(内错角相等,两直线平行)
练习5:如图,已知:AC∥DE,∠1=∠2,
试证明:AB∥CD。
随堂练习
站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
躺在火车上睡觉的旅客
C
练习6: 在以下生活现象中,不是平移现象的是( )
随堂练习
本章的推理是一种演绎推理,通过这样的推理,我们可以完全确信最后结论的正确,体现了数学的严谨性。
在小学我们已经学过相交线和平行线。当时我们只是通过观察,体会相交线与平行线的一些属性。本章在小学学习的基础上,深入学习相交线与平行线,并通过说理的方法从生活中一些基本的事实出发进行推导。
“推理”是数学的一种基本思想,通过推理,我们可以深入理解所研究的对象之间的逻辑关系,而且可以用数学语言清晰地表达这种关系。
相交线
对顶角相等
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与已知直线垂直
平行线
同位角相等,两直线平行
平行线的判定
平行线的性质
两直线平行,同旁内角互补
相交线与平行线
同旁内角互补,两直线平行
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
谢 谢 大 家
相交线与平行线
(复习课)
平昌**中学初一年级
年 月 日
知识回顾
A
B
C
D
1
2
3
4
两直线相交 邻补角 对顶角
分类
判定方法(特点)
性质
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
1、顶点相同,
2、有一条公共边,另一边互为反向延线
1、顶点相同,
2、角的两边互为反向延长线
邻补角互补
对顶角相等
相交线
A
B
C
D
C
D
1
O
垂直
判定
性质
两条直线相交时四个交角中一个角是直角
几何语言:∵∠1=90。 ∴AB⊥CD
若直线AB与CD垂直,垂足为O,那么,∠1=90°
几何语言:∵AB⊥CD ∴ ∠1=90。
两直线垂直
A
B
C
D
1
2
3
4
C
D
E
F
1
2
3
4
5
6
7
8
直线AB、CD称为被截线,直线EF称为截线
同位角 内错角 同旁内角
分类
与被截线关系
与截线关系
∠1和∠5,∠2和∠6 ∠3和∠7,∠4和∠8
∠3和∠5,∠4和∠6
∠3和∠6,∠4和∠5
同侧
同旁
内部
同旁
两旁
内部
三线八角
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角 内错角 同旁内角
判定方法
性质
同位角相等,两直线平行
∵∠1=∠5 ∴AB∥CD
内错角相等,两直线平行
∵∠3= ∠ 5 ∴AB∥CD
∵∠3+∠6=180 ° ∴AB∥CD
同旁内角互补,两直线平行
两直线平行,同位角相等
∵AB∥CD ∴ ∠1=∠5
两直线平行,内错角相等
两直线平行, 同旁内角互补
∵ AB∥CD ∴ ∠3= ∠5
∵ AB∥CD ∴∠3+∠6=180 °
平行线
知识应用
E
D
C
B
A
(已知)
解:(1)证明:∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
已知∠ADE=60 ° ∠B=60 °∠AED=40°
(1)求证:DE∥BC (2) ∠C的度数
回顾
有关同位角、内错角、同旁内角的平分线的关系研究
(1)如图,AB//CD,EP、FQ分别平分∠MEB和∠DFM,求证: EP//FQ
EP、FQ分别平分∠MEB和∠DFM
∠MEB=∠DFM
分析:要求EP//FQ
∠1=∠3
AB//CD
问题1:
(2)如图,AB//CD,EP、FQ分别平分∠AEN和∠DFM,问直线EP与FQ存在什么位置关系?说明你的理由
解:∵ AB//CD( )
∴ ∠AEN=∠DFM ( )
∵ EP、FQ分别平分∠AEN和∠DFM ( )
∴ ∠1=∠ 3( )
∴ EP // FQ( )
已知
两直线平行,内错角相等
已知
角平分线定义
等量代换
内错角相等,两直线平行
∴ ∠1= ∠AEN , ∠ 3= ∠DFM ( )
(3)如图,AB//CD,EQ、FQ分别平分∠BEN和∠DFM,问直线EQ与FQ存在什么位置关系?说明理由
解:∵ AB//CD( )
已知
∴ ∠BEN+∠DFM=180。( )
两直线平行,同旁内角互补
∵ EQ、FQ分别平分∠BEN和∠DFM ( )
已知
角平分线定义
等量代换
∴ ∠ Q=180。-(∠1+∠ 3 )=90。( )
三角形内角和180。
∴ ∠1= ∠BEN , ∠ 3= ∠DFM ( )
∴ ∠1+∠ 3= (∠BEN+∠DFM)=90。( )
∴ EQ ⊥ FQ( )
垂直定义
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.
图(1)
F
解:过点P作直线PF平行直线AB
1
2
∵AB∥CD ∴ AB∥CD ∥PF
∴∠A+∠1=180。 ∠2+∠C=180 。 ∴∠A+∠1+ ∠2+∠C =360 。
∵∠APC=∠1 + ∠2 ∴∠A+ ∠APC +∠C =360 。
探索发现:
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明。
图(2)
F
解:过点P作直线PF平行直线AB
∵AB∥CD, ∴ AB∥CD ∥PF
∴∠A=∠1,∠2=∠C
∵∠APC=∠1 + ∠2 ∴ ∠APC =∠A + ∠C
1
2
探索发现:
如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明。
图(3)
F
图(4)
F
∠A= ∠P +∠C
∠C= ∠P +∠A
探索发现:
A
B
C
D
E
M
N
P
Q
T
小明现在在做一个工艺插件如图3,遇到一个问题,需要大家帮忙,小明已经量得插件的∠D=60 ,∠E= 122 ,要使∠B为多少度时,AB∥CD。
图3
A
B
C
D
E
F
F
练习
有一个与地面成30°角的斜坡,如图②,现要在斜坡上竖一电线杆,当电线杆与斜坡成的∠ 1= °时,电线杆与地面垂直。
1
图②
30°
练习
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结——
例1:如图,三条直线AB,CD,EF相交于O,且CD⊥EF,∠AOE=70 ,若OG平分∠BOF。
求:∠DOG的度数。
典型例题
解:∵ CD⊥EF(已知)
∴ ∠DOF=90 (垂直的定义)
∵ ∠AOE=70 (已知)
∴ ∠BOF=∠AOE=70 (对顶角相等)
∵ OG平分∠BOF,(已知)
∴ ∠FOG= ∠BOF=35 (角的平分线定义)
∴ ∠DOG=∠DOF-∠FOG
=90 -35 =55
例2:如图所示,直线a、b被c、d所截,且c⊥a,c⊥b.∠1与∠2的相等吗?说明理由。
典型例题
解:∠1与∠2 的度数相等。理由如下:
∵ c⊥a c⊥b(已知)
∴ ∠3=∠4=90 (垂直的定义)
∴ a//b(同位角相等,两直线平行)
∴ ∠5=∠2(两直线平行,同位角相等)
∵ ∠5=∠1(对顶角相等)
∴ ∠2=∠1(等量代换)
d
c
a
b
C
∟
理由:垂线段最短
例3:如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
典型例题
∠1和∠2不是同位角,
练习1:如图中的∠1和∠2是同位角吗 为什么
1
2
1
2
因为∠1和∠2无一边共线。
∠1和∠2是同位角,
因为∠1和∠2有一边共线、同向且不共定点。
随堂练习
A
C
B
D
E
1
2
答:∠EAC
答:∠DAB
答:∠BAC ∠BAE ∠2
2)∠1与哪个角是同旁内角?
3)∠2与哪个角是内错角
1)∠1与哪个角是内错角?
练习2:如图,回答一下问题:
随堂练习
证明: ∵ ∠DAC= ∠ACB (已知)
A
B
C
D
E
F
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
练习3:已知 ∠DAC= ∠ACB, ∠D+∠DFE=180°,
求证:EF//BC
随堂练习
证明:∵∠1+∠2=180°(已知)
4
1
2
3
A
B
C
E
F
D
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
∴∠3+∠4=180°
(等量代换)
∴ AB//CD
练习4:如图 已知:∠1+∠2=180°,
求证:AB∥CD。
随堂练习
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴ AB ∥ CD
(内错角相等,两直线平行)
练习5:如图,已知:AC∥DE,∠1=∠2,
试证明:AB∥CD。
随堂练习
站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
躺在火车上睡觉的旅客
C
练习6: 在以下生活现象中,不是平移现象的是( )
随堂练习
本章的推理是一种演绎推理,通过这样的推理,我们可以完全确信最后结论的正确,体现了数学的严谨性。
在小学我们已经学过相交线和平行线。当时我们只是通过观察,体会相交线与平行线的一些属性。本章在小学学习的基础上,深入学习相交线与平行线,并通过说理的方法从生活中一些基本的事实出发进行推导。
“推理”是数学的一种基本思想,通过推理,我们可以深入理解所研究的对象之间的逻辑关系,而且可以用数学语言清晰地表达这种关系。
相交线
对顶角相等
过一点有且只有一条直线与已知直线垂直
过直线外一点有且只有一条直线与已知直线垂直
平行线
同位角相等,两直线平行
平行线的判定
平行线的性质
两直线平行,同旁内角互补
相交线与平行线
同旁内角互补,两直线平行
内错角相等,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
谢 谢 大 家
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
