2022-2023学年鲁教版(五四学制)七年级数学下册《第8章平行线的有关证明》期末综合复习训练题(含解析)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)七年级数学下册《第8章平行线的有关证明》期末综合复习训练题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 488.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 10:14:21 | ||
图片预览


文档简介
2022-2023学年鲁教版(五四学制)七年级数学下册《第8章平行线的有关证明》
期末综合复习训练题(附答案)
一、单选题
1.下列命题中,是真命题的是( )
A.相等的角是对顶角 B.在同一平面内,不相交的两条线段平行
C.一个角的余角比它的补角小90° D.过一点有且只有一条直线与已知直线平行
2.在第届全国中学生物理竞赛决赛中,华师一物理竞赛团队有位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,说:是,说:是,说:是,说:说错了,说:不是我.教练说:你们中只有一人说对了,那么第一名是( )
A.B B.C C.D D.E
3.如图,下列说法错误的是( )
A.如果∠AED=∠C,则 DE//BC
B.如果∠1=∠2,则 BD//EF
C.如果AB//EF,则∠FEC=∠A
D.如果∠ABC+∠BDE=180°,则AB//EF
4.如图,直线直线分别交于点A、C两点,过点A作交直线b于点B,若,则的度数是( )
A. B. C. D.
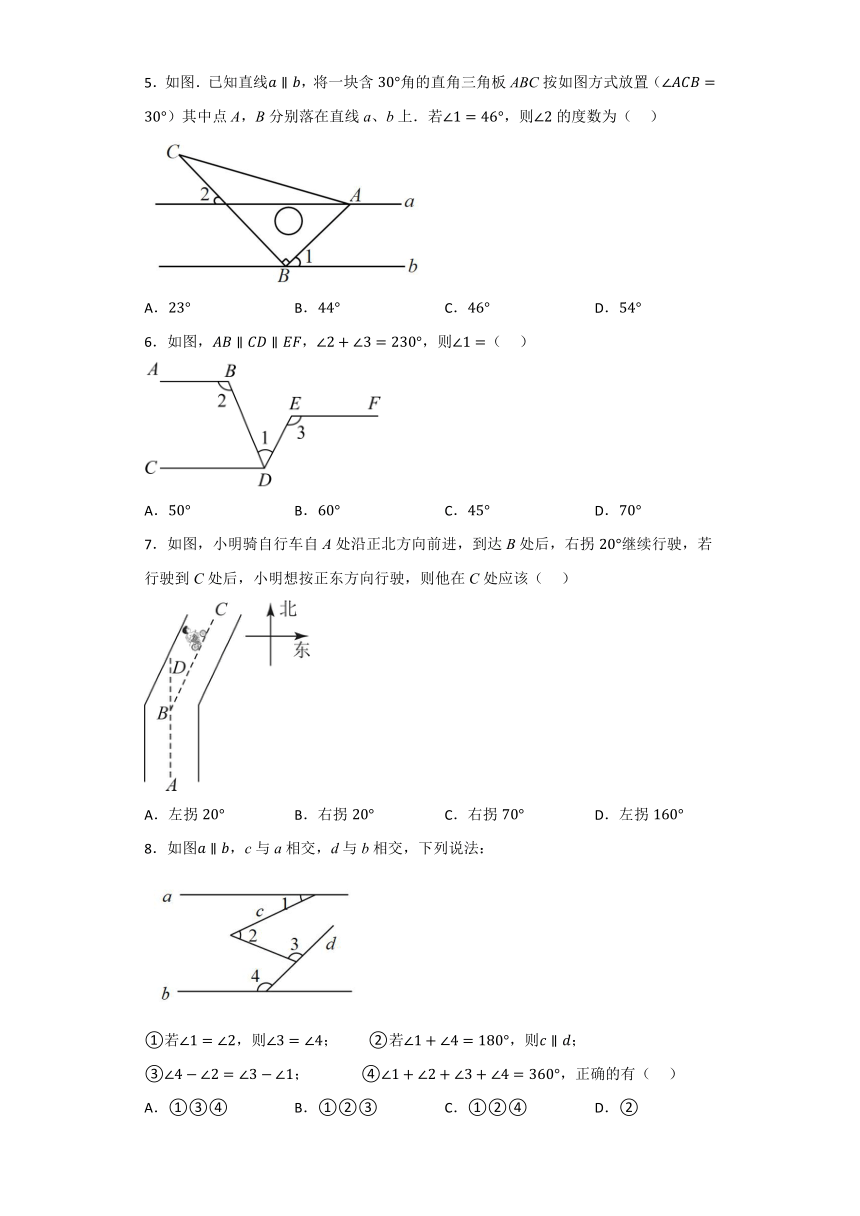
5.如图.已知直线,将一块含角的直角三角板ABC按如图方式放置()其中点A,B分别落在直线a、b上.若,则的度数为( )
A. B. C. D.
6.如图,,,则( )
A. B. C. D.
7.如图,小明骑自行车自A处沿正北方向前进,到达B处后,右拐继续行驶,若行驶到C处后,小明想按正东方向行驶,则他在C处应该( )
A.左拐 B.右拐 C.右拐 D.左拐
8.如图,c与a相交,d与b相交,下列说法:
①若,则; ②若,则;
③; ④,正确的有( )
A.①③④ B.①②③ C.①②④ D.②
二、填空题
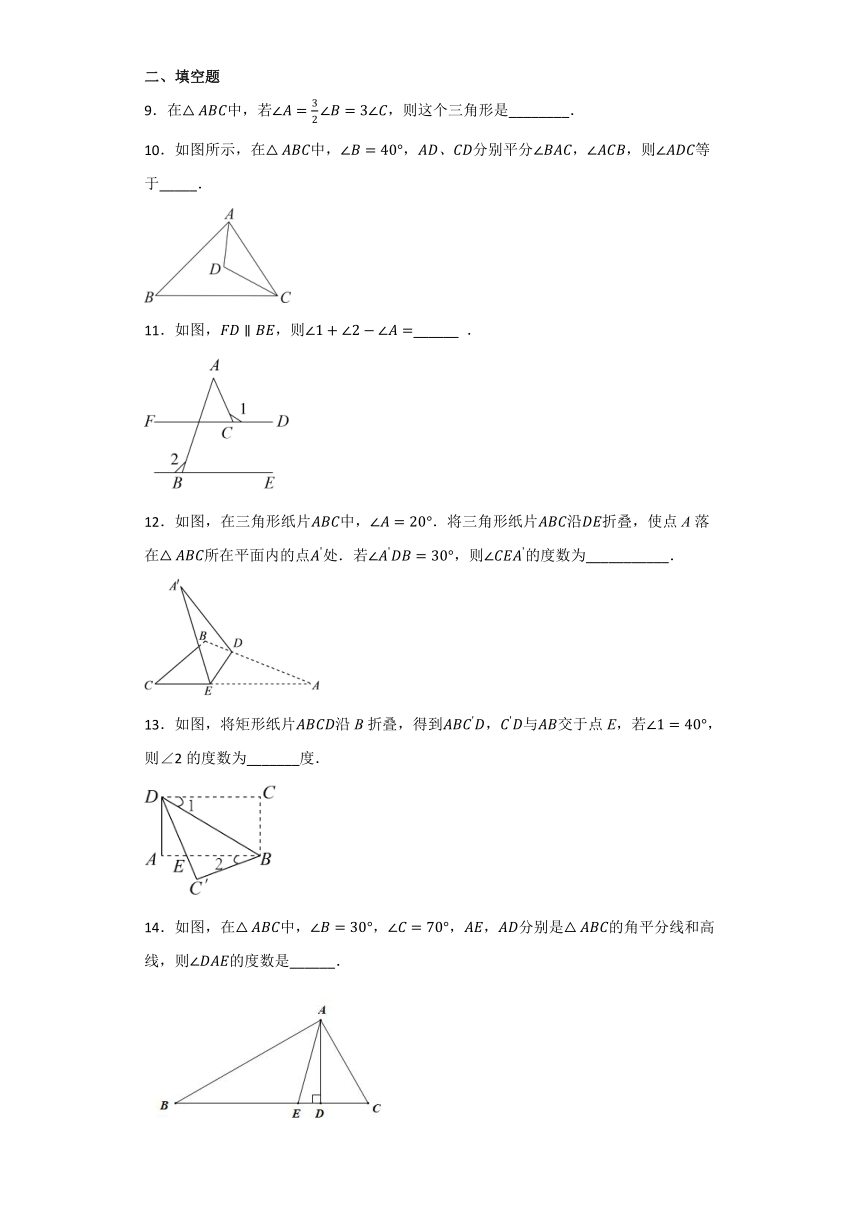
9.在中,若,则这个三角形是________.
10.如图所示,在中,,、分别平分,,则等于_____.
11.如图,,则______ .
12.如图,在三角形纸片中,.将三角形纸片沿折叠,使点A落在所在平面内的点处.若,则的度数为___________.
13.如图,将矩形纸片沿B折叠,得到,与交于点E,若,则∠2的度数为_______度.
14.如图,在中,,,,分别是的角平分线和高线,则的度数是______.
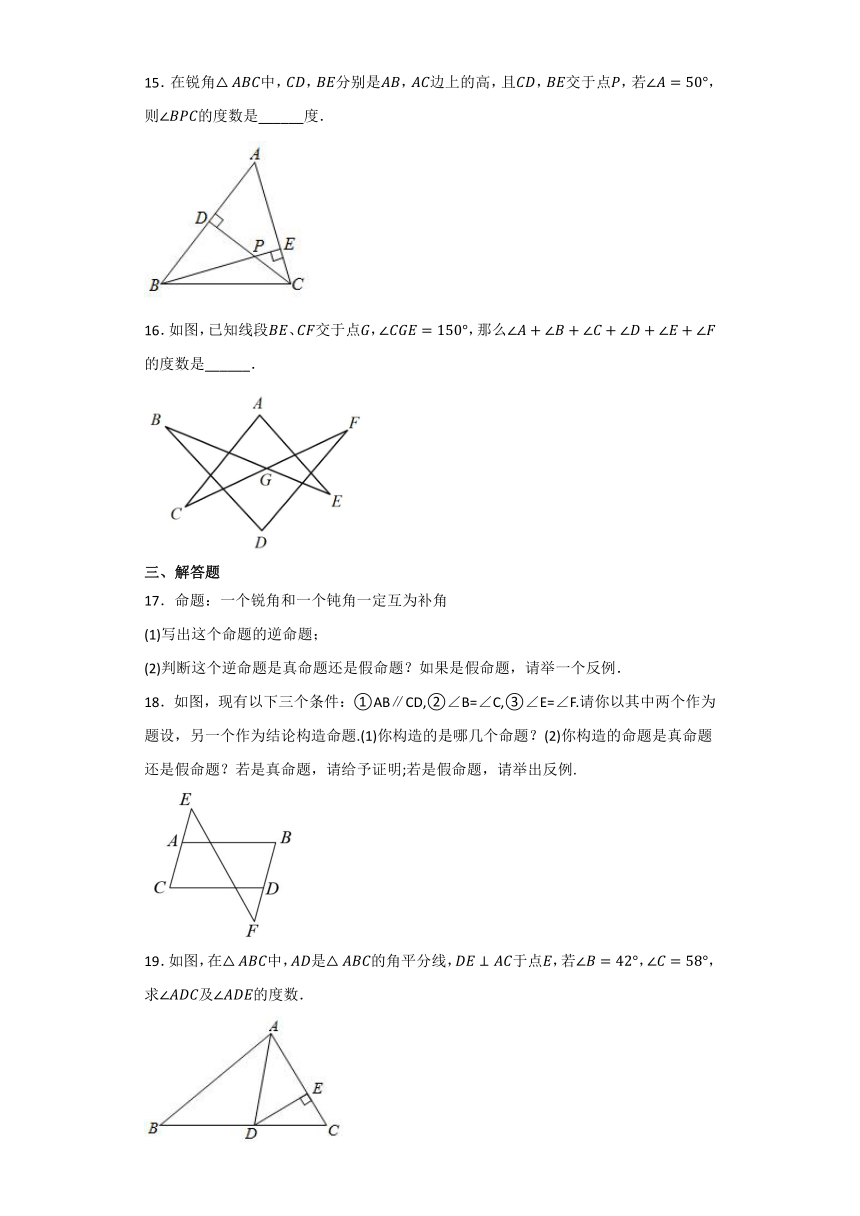
15.在锐角中,,分别是,边上的高,且,交于点,若,则的度数是______度.
16.如图,已知线段、交于点,,那么的度数是______.
三、解答题
17.命题:一个锐角和一个钝角一定互为补角
(1)写出这个命题的逆命题;
(2)判断这个逆命题是真命题还是假命题?如果是假命题,请举一个反例.
18.如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例.
19.如图,在中,是的角平分线,于点,若,,求及的度数.
20.如图,,.
(1)试说明:;
(2)如果平分,求.
21.在中,,平分,F为射线上一点(不与点E重合),且于D.
(1)如果点F与点A重合,且,,如图1,求的度数;
(2)如果点F在线段上(不与点A重合),如图2,求证:;
(3)如果点F在外部,如图3,此时与的数量关系是否发生变化?请说明理由.
22.如图1,已知两条直线被直线所截,分别交于点E,点F,平分交于点M,且.
(1)判断直线与直线是否平行,并说明理由;
(2)如图2,点G是射线上一动点(不与点M,F重合),平分交于点H,过点H作于点N,设.
①当点G在点F的右侧时,若,求的度数;
②当点G在运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明.
参考答案
1.解:A、相等的角不一定是对顶角,故此选项不符合题意;
B、在同一平面内,不相交的两条直线平行,两条线段不一定平行,故此选项不符合题意;
C、设一个角为x,则其余角为,其补角为,
∵,
∴此选项符合题意;
D、过直线外一点有且只有一条直线与已知直线平行,故此选项不符合题意;
故选C.
2.解:说:是,说:说错了,教练说:你们中只有一人说对了,
∴和的说法只能一真一假,不能同真,也不能同假;
∴和,说得都是假话,
∴只有说对了,
故选:.
3.解:A、∠AED=∠C,则 DE//BC,故原选项正确,不符合题意;
B、∠1=∠2,则 BD//EF,故原选项正确,不符合题意;
C、AB//EF,则∠FEC=∠A,故原选项正确,不符合题意;
D、∠ABC+∠BDE=180°,则BC//DE,故原选项错误,符合题意.
故选:D.
4.解:
如图,
∵,
∴,
∵,
∴,
∴.
故选:C
5.解:如图,
∵,
∴.
∵,
∴.
故选B.
6.解:∵,
∴,,
∴,
∵,
∴,
∴.
故选:A
7.解:过点B作于点B,过点C作,并标记角,如图所示.
∵,
∴.
∵,
∴.
∴若小明想按正东方向行驶,则他在C处应该右拐70°,故选C.
8.解:如图所示,
若,则,则,故该选项正确;
若,由可得, ,则,则,故该选项正确;
由可得,,由得:,则,故该说法正确;
由③得,只有时,,故该说法错误;
故选:B.
9.解:∵
∴ ,
又∵ ,
∴ ,
解得:,
∴这个三角形是直角三角形.
故答案为:直角三角形.
10.解:∵在中,,
∴,
∵、分别平分,,
∴,
∴.
故答案为:.
11.解:,
,,
,
.
故答案为:.
12.解:根据折叠,可得,
,
,
,
,
,
,
,
故答案为:.
13.解:在矩形中,,,
∴,
∵,
∴,
由折叠可知:,
∴,
∴.
故答案为:10.
14.解:∵,,
∴.
∵是的平分线,
∴.
在中,,,
∴,
∴.
故答案为:.
15.解:∵,分别是,边上的高,
∴,
∴,
∴.
故答案为:.
16.解:如图:
∵,
,
∴;
故答案为:.
17.解:(1)原命题中,条件为“一个锐角和一个钝角”,结论为“这两个角一定互为补角”,将条件与结论互换,得到逆命题,即“互补的两个角一定是一个锐角,一个钝角”.
(2)∵互补的两个角可以都为直角,
∴“互补的两个角一定是一个锐角,一个钝角”是假命题.
反例是“两个角都是直角”.
18.解:(1)由①②得到③;由①③得到②;由②③得到①,
(2)∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
所以由①②得到③为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
所以由①③得到②为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
所以由②③得到①为真命题.
19.解:,,
,
平分,
,
,
,
,
.
20.(1)解:∵在中,,,
∴,
∵,
∴.
(2)解:∵,平分,
∴,
∵,
∴,
21.(1)解:∵,,,
∴,,
∵平分,
∴,
∴;
(2)证明:∵,
∴,
∵平分,
∴,
在中
,
∵,
∴;
(3)解:不发生变化,理由如下,
∵,
∴,
∵平分,
∴,
在中
,
∴,
∵,
∴.
22.(1)解:结论:.
理由:如图1中,
∵平分交于点M,
∴,
∵.
∴,
∴.
(2)解:①如图2中,
∵,
∴,
∵,
∴.
∴,
∵平分,
∴,
∵,
∴,
∴,则,
∵,
∴;
②猜想:或
理由:(1)当点G在F的右侧时,
∵,
∴,
∴,
∵,
∴,
∵,∴,
∴.
(2)当点G在F的左侧时,
∵,
∴,
∵平分,平分,
∵,
∴,
∵,
∴,
∴.
综上所述,或.
期末综合复习训练题(附答案)
一、单选题
1.下列命题中,是真命题的是( )
A.相等的角是对顶角 B.在同一平面内,不相交的两条线段平行
C.一个角的余角比它的补角小90° D.过一点有且只有一条直线与已知直线平行
2.在第届全国中学生物理竞赛决赛中,华师一物理竞赛团队有位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,说:是,说:是,说:是,说:说错了,说:不是我.教练说:你们中只有一人说对了,那么第一名是( )
A.B B.C C.D D.E
3.如图,下列说法错误的是( )
A.如果∠AED=∠C,则 DE//BC
B.如果∠1=∠2,则 BD//EF
C.如果AB//EF,则∠FEC=∠A
D.如果∠ABC+∠BDE=180°,则AB//EF
4.如图,直线直线分别交于点A、C两点,过点A作交直线b于点B,若,则的度数是( )
A. B. C. D.
5.如图.已知直线,将一块含角的直角三角板ABC按如图方式放置()其中点A,B分别落在直线a、b上.若,则的度数为( )
A. B. C. D.
6.如图,,,则( )
A. B. C. D.
7.如图,小明骑自行车自A处沿正北方向前进,到达B处后,右拐继续行驶,若行驶到C处后,小明想按正东方向行驶,则他在C处应该( )
A.左拐 B.右拐 C.右拐 D.左拐
8.如图,c与a相交,d与b相交,下列说法:
①若,则; ②若,则;
③; ④,正确的有( )
A.①③④ B.①②③ C.①②④ D.②
二、填空题
9.在中,若,则这个三角形是________.
10.如图所示,在中,,、分别平分,,则等于_____.
11.如图,,则______ .
12.如图,在三角形纸片中,.将三角形纸片沿折叠,使点A落在所在平面内的点处.若,则的度数为___________.
13.如图,将矩形纸片沿B折叠,得到,与交于点E,若,则∠2的度数为_______度.
14.如图,在中,,,,分别是的角平分线和高线,则的度数是______.
15.在锐角中,,分别是,边上的高,且,交于点,若,则的度数是______度.
16.如图,已知线段、交于点,,那么的度数是______.
三、解答题
17.命题:一个锐角和一个钝角一定互为补角
(1)写出这个命题的逆命题;
(2)判断这个逆命题是真命题还是假命题?如果是假命题,请举一个反例.
18.如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.(1)你构造的是哪几个命题?(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例.
19.如图,在中,是的角平分线,于点,若,,求及的度数.
20.如图,,.
(1)试说明:;
(2)如果平分,求.
21.在中,,平分,F为射线上一点(不与点E重合),且于D.
(1)如果点F与点A重合,且,,如图1,求的度数;
(2)如果点F在线段上(不与点A重合),如图2,求证:;
(3)如果点F在外部,如图3,此时与的数量关系是否发生变化?请说明理由.
22.如图1,已知两条直线被直线所截,分别交于点E,点F,平分交于点M,且.
(1)判断直线与直线是否平行,并说明理由;
(2)如图2,点G是射线上一动点(不与点M,F重合),平分交于点H,过点H作于点N,设.
①当点G在点F的右侧时,若,求的度数;
②当点G在运动过程中,和之间有怎样的数量关系?请写出你的猜想,并加以证明.
参考答案
1.解:A、相等的角不一定是对顶角,故此选项不符合题意;
B、在同一平面内,不相交的两条直线平行,两条线段不一定平行,故此选项不符合题意;
C、设一个角为x,则其余角为,其补角为,
∵,
∴此选项符合题意;
D、过直线外一点有且只有一条直线与已知直线平行,故此选项不符合题意;
故选C.
2.解:说:是,说:说错了,教练说:你们中只有一人说对了,
∴和的说法只能一真一假,不能同真,也不能同假;
∴和,说得都是假话,
∴只有说对了,
故选:.
3.解:A、∠AED=∠C,则 DE//BC,故原选项正确,不符合题意;
B、∠1=∠2,则 BD//EF,故原选项正确,不符合题意;
C、AB//EF,则∠FEC=∠A,故原选项正确,不符合题意;
D、∠ABC+∠BDE=180°,则BC//DE,故原选项错误,符合题意.
故选:D.
4.解:
如图,
∵,
∴,
∵,
∴,
∴.
故选:C
5.解:如图,
∵,
∴.
∵,
∴.
故选B.
6.解:∵,
∴,,
∴,
∵,
∴,
∴.
故选:A
7.解:过点B作于点B,过点C作,并标记角,如图所示.
∵,
∴.
∵,
∴.
∴若小明想按正东方向行驶,则他在C处应该右拐70°,故选C.
8.解:如图所示,
若,则,则,故该选项正确;
若,由可得, ,则,则,故该选项正确;
由可得,,由得:,则,故该说法正确;
由③得,只有时,,故该说法错误;
故选:B.
9.解:∵
∴ ,
又∵ ,
∴ ,
解得:,
∴这个三角形是直角三角形.
故答案为:直角三角形.
10.解:∵在中,,
∴,
∵、分别平分,,
∴,
∴.
故答案为:.
11.解:,
,,
,
.
故答案为:.
12.解:根据折叠,可得,
,
,
,
,
,
,
,
故答案为:.
13.解:在矩形中,,,
∴,
∵,
∴,
由折叠可知:,
∴,
∴.
故答案为:10.
14.解:∵,,
∴.
∵是的平分线,
∴.
在中,,,
∴,
∴.
故答案为:.
15.解:∵,分别是,边上的高,
∴,
∴,
∴.
故答案为:.
16.解:如图:
∵,
,
∴;
故答案为:.
17.解:(1)原命题中,条件为“一个锐角和一个钝角”,结论为“这两个角一定互为补角”,将条件与结论互换,得到逆命题,即“互补的两个角一定是一个锐角,一个钝角”.
(2)∵互补的两个角可以都为直角,
∴“互补的两个角一定是一个锐角,一个钝角”是假命题.
反例是“两个角都是直角”.
18.解:(1)由①②得到③;由①③得到②;由②③得到①,
(2)∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
所以由①②得到③为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
所以由①③得到②为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
所以由②③得到①为真命题.
19.解:,,
,
平分,
,
,
,
,
.
20.(1)解:∵在中,,,
∴,
∵,
∴.
(2)解:∵,平分,
∴,
∵,
∴,
21.(1)解:∵,,,
∴,,
∵平分,
∴,
∴;
(2)证明:∵,
∴,
∵平分,
∴,
在中
,
∵,
∴;
(3)解:不发生变化,理由如下,
∵,
∴,
∵平分,
∴,
在中
,
∴,
∵,
∴.
22.(1)解:结论:.
理由:如图1中,
∵平分交于点M,
∴,
∵.
∴,
∴.
(2)解:①如图2中,
∵,
∴,
∵,
∴.
∴,
∵平分,
∴,
∵,
∴,
∴,则,
∵,
∴;
②猜想:或
理由:(1)当点G在F的右侧时,
∵,
∴,
∴,
∵,
∴,
∵,∴,
∴.
(2)当点G在F的左侧时,
∵,
∴,
∵平分,平分,
∵,
∴,
∵,
∴,
∴.
综上所述,或.
同课章节目录
