2022-2023学年鲁教版(五四学制)七年级数学下册《第10章三角形的有关证明》期末综合复习训练题(含解析)
文档属性
| 名称 | 2022-2023学年鲁教版(五四学制)七年级数学下册《第10章三角形的有关证明》期末综合复习训练题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 536.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 10:24:25 | ||
图片预览


文档简介
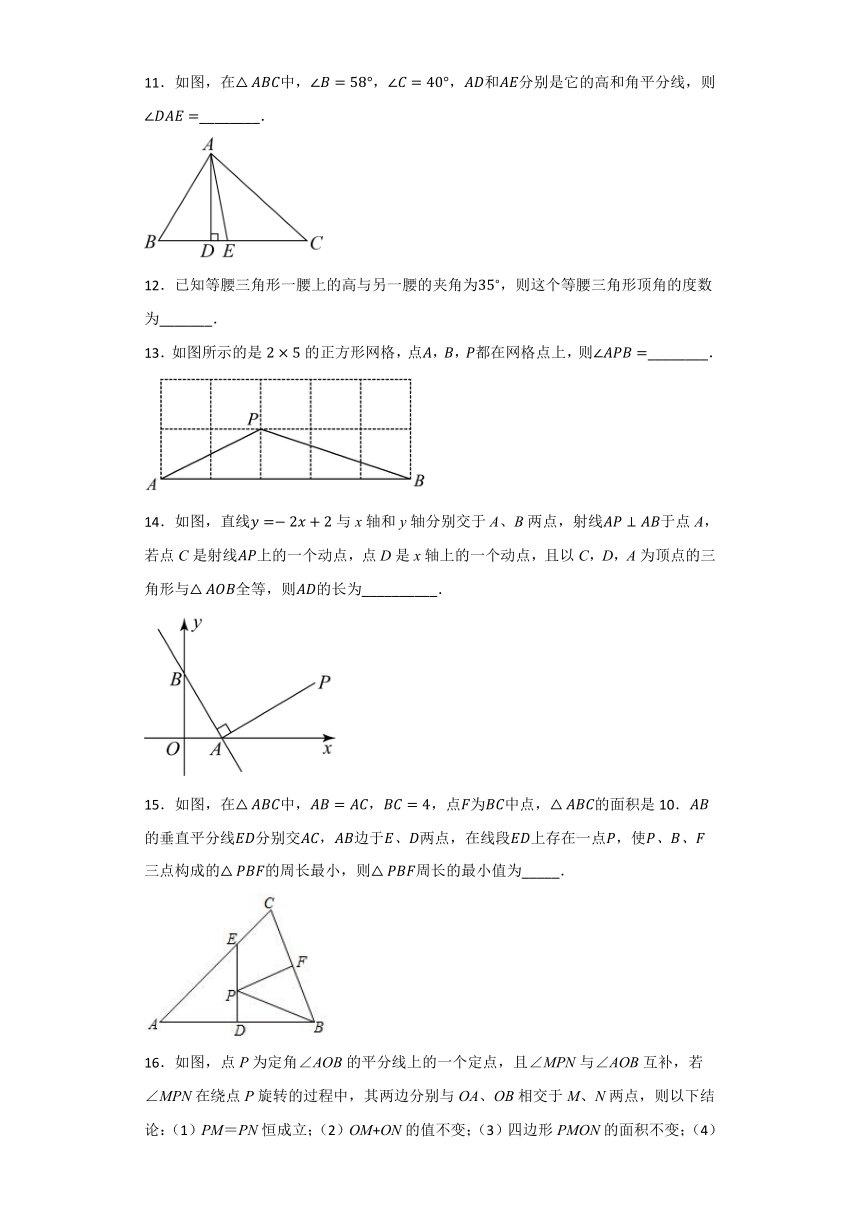
2022-2023学年鲁教版(五四学制)七年级数学下册《第10章三角形的有关证明》
期末综合复习训练题(附答案)
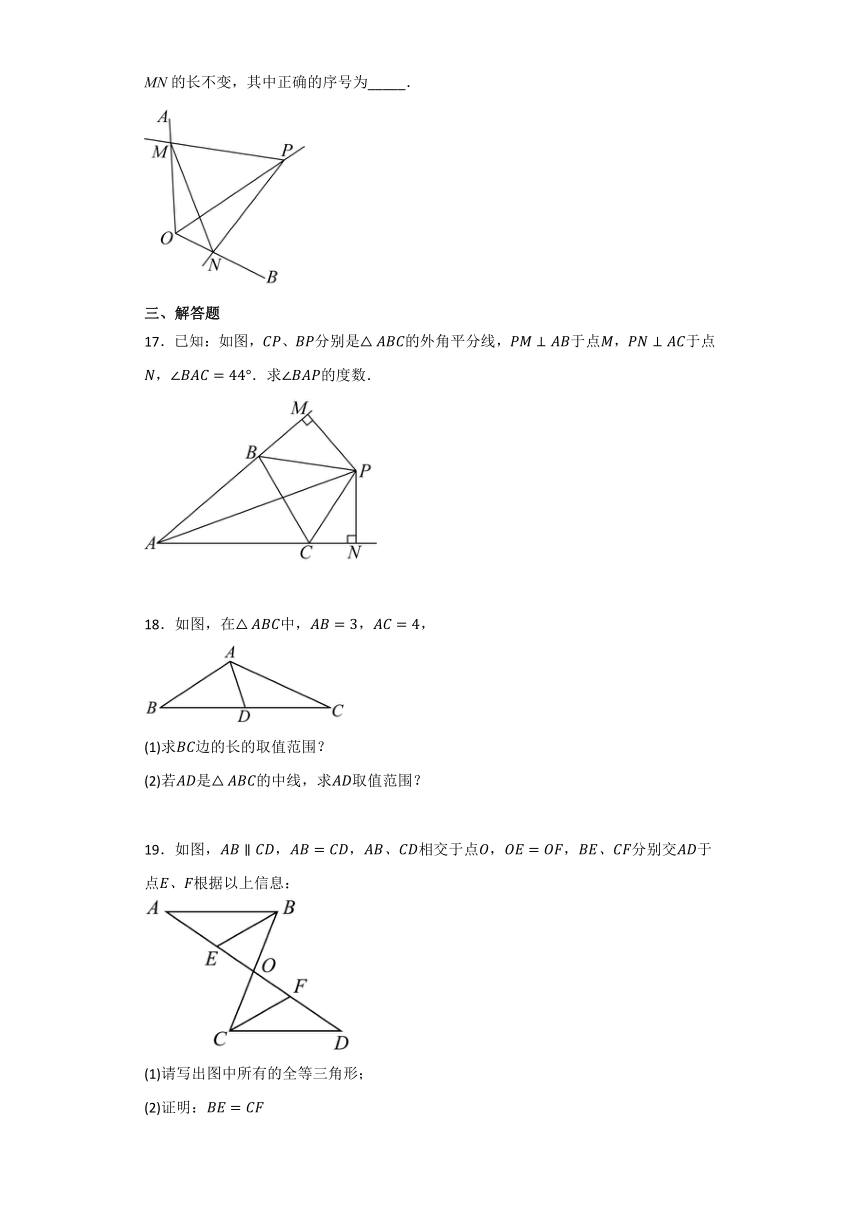
一、单选题
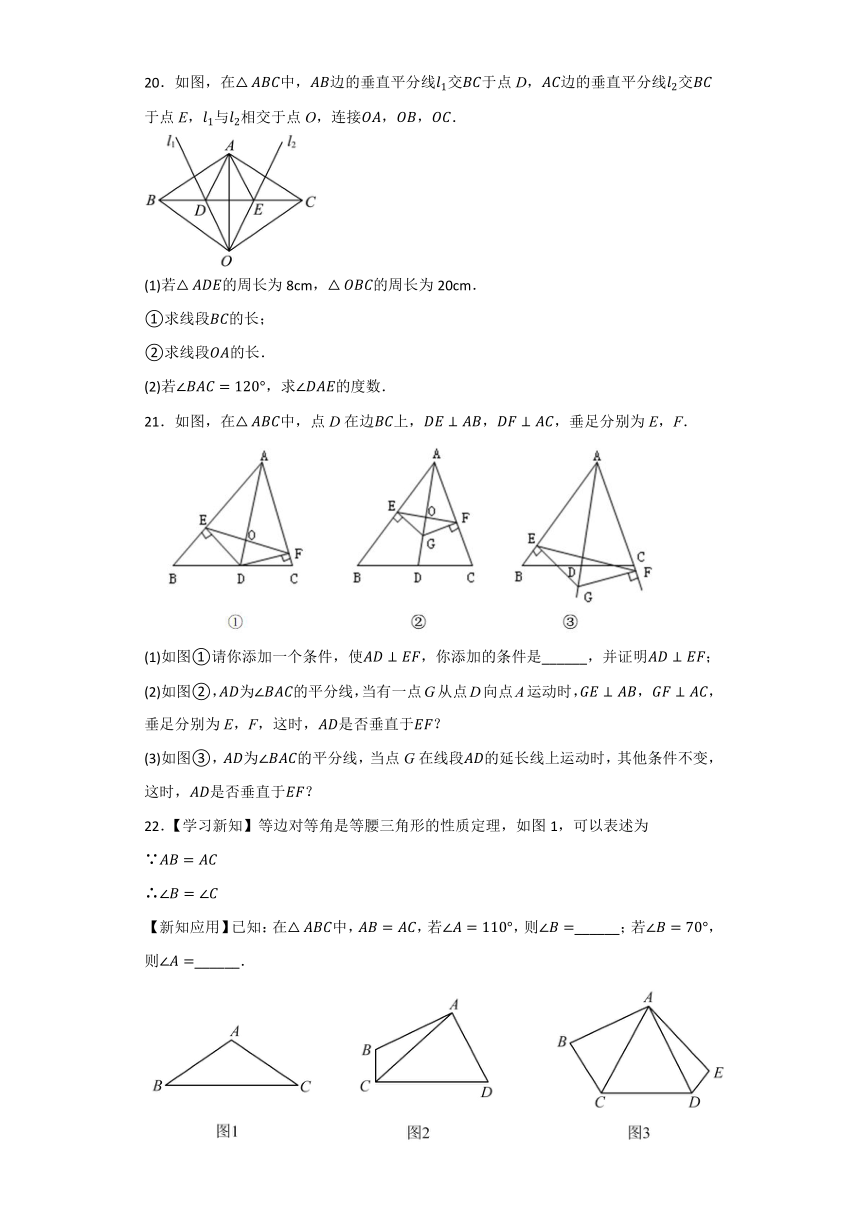
1.若等腰三角形的两边长分别为3和6,则该三角形的周长可能是( )
A.11 B.12 C.15 D.12或15
2.下列说法中,正确的是( )
A.周长相等的两个直角三角形全等 B.周长相等的两个钝角三角形全等
C.周长相等的两个等腰三角形全等 D.周长相等的两个等边三角形全等
3.用反证法证明“三角形中最多有一个直角或钝角”,第一步应假设( )
A.三角形中至少有一个直角或钝角 B.三角形中至少有两个直角或钝角
C.三角形中没有直角或钝角 D.三角形中三个角都是直角或钝角
4.如图,中,,的垂直平分线分别交、于D、E,若,则等于( )
A.1 B. C. D.
5.如图,中,,点在上,,若,则的度数是( )
A. B. C. D.
6.如图,,.点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为.当与全等时,的值是( )
A.2 B.1或 C.2或 D.1或2
7.如图,在中,平分,平分,点是、的垂直平分线的交点,连接、,若,则的大小为( )
A. B. C. D.
8.如图,,的平分线相交于,过点作,交于,交于,那么下列结论中:①;②;③;④的周长,其中正确的有几个( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,D在上,E在上,且,补充一个条件______后,可用“”判断.
10.如图,已知,,,以、两点为圆心,大于的长为半径画圆弧,两弧相交于点M,N,连接与相交于点D,则的周长为_________.
11.如图,在中,,,和分别是它的高和角平分线,则________.
12.已知等腰三角形一腰上的高与另一腰的夹角为,则这个等腰三角形顶角的度数为_______.
13.如图所示的是的正方形网格,点,,都在网格点上,则________.
14.如图,直线与x轴和y轴分别交于A、B两点,射线于点A,若点C是射线上的一个动点,点D是x轴上的一个动点,且以C,D,A为顶点的三角形与全等,则的长为__________.
15.如图,在中,,点为中点,的面积是10.的垂直平分线分别交边于两点,在线段上存在一点,使三点构成的的周长最小,则周长的最小值为_____.
16.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的序号为_____.
三、解答题
17.已知:如图,、分别是的外角平分线,于点,于点,.求的度数.
18.如图,在中,,
(1)求边的长的取值范围?
(2)若是的中线,求取值范围?
19.如图,,,相交于点,,分别交于点根据以上信息:
(1)请写出图中所有的全等三角形;
(2)证明:
20.如图,在中,边的垂直平分线交于点D,边的垂直平分线交于点E,与相交于点O,连接.
(1)若的周长为8cm,的周长为20cm.
①求线段的长;
②求线段的长.
(2)若,求的度数.
21.如图,在中,点D在边上,,垂足分别为E,F.
(1)如图①请你添加一个条件,使,你添加的条件是______,并证明;
(2)如图②,为的平分线,当有一点G从点D向点A运动时,,垂足分别为E,F,这时,是否垂直于?
(3)如图③,为的平分线,当点G在线段的延长线上运动时,其他条件不变,这时,是否垂直于?
22.【学习新知】等边对等角是等腰三角形的性质定理,如图1,可以表述为
∵
∴
【新知应用】已知:在中,,若,则______;若,则______.
【尝试探究】如图2,四边形中,,,若连接,则平分.
某数学小组成员通过观察、实验,提出以下想法:延长到点,使得,连接,利用三角形全等的判定和等腰三角形的性质可以证明.请你参考他们的想法,写出完整的证明过程.
【拓展应用】借助上一问的尝试,继续探究:如图3所示,在五边形中,,,,连接,平分吗 请说明理由.
参考答案
1.解:等腰三角形的两边长分别为3和6,
当腰为3,底为6时,,不能构成三角形;
当腰为6,底为3时,能构成三角形,周长为,
故选:C.
2.解:周长相等的两个直角三角形不一定全等,故A选项不符合题意;
周长相等的两个钝角三角形不一定全等,故B选项不符合题意;
周长相等的两个等腰三角形不一定全等,故C选项不符合题意;
周长相等的两个等边三角形,三边对应相等,根据SSS可证这两个等边三角形全等,故D选项符合题意,
故选:D;
3.解:用反证法证明“三角形中最多有一个直角或钝角”,
第一步应假设三角形中至少有两个直角或钝角,
故选:B.
4.解:∵的垂直平分线分别交、于D、E,
∴,
∴,
∴,
∴,
∴,
∴;
故选D.
5.解: ,,,
,
,
,
,
,
故选:B.
6.解:由题意知,,,,
与全等,分两种情况求解:
①当时,,即,解得;
②当时,,即,解得,,即,解得;
综上所述,的值是1或,
故选:B.
7.解:连接并延长至D,如图,
∵点O是、的垂直平分线的交点,
∴,
∴,
∵是的一个外角,
∴,
同理,,
∴,
∴,
∴,
∵平分,平分,
∴,,
∴,
∴,
故选:C.
8.解:,
,,
中,与的平分线交于点,
,,
,,
,,
即和都是等腰三角形;
故①正确;
不一定等于,
不一定等于,
与不一定相等,
与不一定相等,故②错误.
在中,和的平分线相交于点,
,
,
;故③正确;
的周长为:;
故④正确;
故选:C.
9.解:∵,,
∴若用“”判断,可补充的条件是或;
故答案为:或.
10.解:由题意得是的垂直平分线,
,
,
的周长.
故答案为:11.
11.解:∵,,
∴,
∵是三角形的角平分线,
∴,
∵是三角形的高,
∴,
∴,
∴,
故答案为:.
12.解:如图,
,,
.
,
.
如图,,,
.
,
,
.
综上所述,这个等腰三角形顶角的度数为或.
故答案为:或
13.解:延长至,连接,
,
,
,即,
是等腰直角三角形,
,
∴,
故答案为:.
14.解:∵直线与x轴和y轴分别交与A、B两点,
当时,即,
解得:.
当时,,
∴.
∴.
∴.
∵,点C在射线上,
∴,即.
∵,
∴.
若以C、D、A为顶点的三角形与全等,则或,即或.
如图1所示,
当时,;
如图2所示,
当时,.
综上所述,的长为2或.
故答案为:2或.
15.解:是线段的垂直平分线,
与关于对称,
如图所示,连接,交于点,
,
,
周长,
当三点共线时,的周长最小,为的长,
为边的中点,,,
,,
,
,
周长,
周长的最小值为7,
故答案为:7.
16.解:如图作于E,于F.
∵,
∴,
∵,
∴,
∴,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在Rt△POE和Rt△POF中,
,
∴Rt△POE≌Rt△POF,
∴OE=OF,
在△PEM和△PFN中,
∴△PEM≌△PFN,
∴EM=NF,PM=PN,故(1)正确,
∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故(3)正确,
∵,故(2)正确,
∵M,N的位置变化,∴MN的长度是变化的,故(4)错误.
故答案为:(1)(2)(3)
17.解:作于点D,如图所示,
∵是的外角平分线,,,
∴,
同理,
∴,又,,
∴平分,
∵,
∴.
18.(1)解:由三角形的三边关系可知:,
∵,
∴;
(2)解:延长至E,使,连接,
在中,∵,
∴,
∴,
由三角形的三边关系:,
∴,
∴.
19.(1)解:∵,
∴,
∵,
∴,
∴,
∵,,
∴;
∵,
∴,
∴;
(2)证明:由(1)得,
∴.
20.解:(1)①∵是边的垂直平分线,
∴,
∵是边的垂直平分线,
∴,
∴;
②∵是边的垂直平分线,
∴,
∵是边的垂直平分线,
∴,
∵,
∴;
(2),
,
,
,
.
21.(1)解:答案不唯一,如平分,
证明如下:
∵平分,
∴,
∵
∴
又,
∴,
∴
∴垂直于,即;
(2) ,理由如下:
∵平分,
∴,
∵
∴
又,
∴,
∴
∴垂直于,即;
(3) ,理由如下:
∵平分,
∴,
∵
∴
又,
∴,
∴
∴垂直于,即.
22.解:新知应用:
∵,
∴,
若,则;
若,则,
∴;
故答案是;
尝试探究:
证明:如图,延长到点,使得,连接,
∵,
又∵,
∴,
∵在和中,
,
∴,
∴,,
又∵,
∴,
∴,
即平分;
拓展应用:
证明:连接,延长到,使,连接,
∵,,
∴
∵在和中,
,
∴,
∴,,
又∵,,
∴
在和中,
,
∴,
∴,
∴,
即平分;
期末综合复习训练题(附答案)
一、单选题
1.若等腰三角形的两边长分别为3和6,则该三角形的周长可能是( )
A.11 B.12 C.15 D.12或15
2.下列说法中,正确的是( )
A.周长相等的两个直角三角形全等 B.周长相等的两个钝角三角形全等
C.周长相等的两个等腰三角形全等 D.周长相等的两个等边三角形全等
3.用反证法证明“三角形中最多有一个直角或钝角”,第一步应假设( )
A.三角形中至少有一个直角或钝角 B.三角形中至少有两个直角或钝角
C.三角形中没有直角或钝角 D.三角形中三个角都是直角或钝角
4.如图,中,,的垂直平分线分别交、于D、E,若,则等于( )
A.1 B. C. D.
5.如图,中,,点在上,,若,则的度数是( )
A. B. C. D.
6.如图,,.点在线段上以的速度由点向点运动,同时,点在线段上以的速度由点向点运动,它们运动的时间为.当与全等时,的值是( )
A.2 B.1或 C.2或 D.1或2
7.如图,在中,平分,平分,点是、的垂直平分线的交点,连接、,若,则的大小为( )
A. B. C. D.
8.如图,,的平分线相交于,过点作,交于,交于,那么下列结论中:①;②;③;④的周长,其中正确的有几个( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,D在上,E在上,且,补充一个条件______后,可用“”判断.
10.如图,已知,,,以、两点为圆心,大于的长为半径画圆弧,两弧相交于点M,N,连接与相交于点D,则的周长为_________.
11.如图,在中,,,和分别是它的高和角平分线,则________.
12.已知等腰三角形一腰上的高与另一腰的夹角为,则这个等腰三角形顶角的度数为_______.
13.如图所示的是的正方形网格,点,,都在网格点上,则________.
14.如图,直线与x轴和y轴分别交于A、B两点,射线于点A,若点C是射线上的一个动点,点D是x轴上的一个动点,且以C,D,A为顶点的三角形与全等,则的长为__________.
15.如图,在中,,点为中点,的面积是10.的垂直平分线分别交边于两点,在线段上存在一点,使三点构成的的周长最小,则周长的最小值为_____.
16.如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的序号为_____.
三、解答题
17.已知:如图,、分别是的外角平分线,于点,于点,.求的度数.
18.如图,在中,,
(1)求边的长的取值范围?
(2)若是的中线,求取值范围?
19.如图,,,相交于点,,分别交于点根据以上信息:
(1)请写出图中所有的全等三角形;
(2)证明:
20.如图,在中,边的垂直平分线交于点D,边的垂直平分线交于点E,与相交于点O,连接.
(1)若的周长为8cm,的周长为20cm.
①求线段的长;
②求线段的长.
(2)若,求的度数.
21.如图,在中,点D在边上,,垂足分别为E,F.
(1)如图①请你添加一个条件,使,你添加的条件是______,并证明;
(2)如图②,为的平分线,当有一点G从点D向点A运动时,,垂足分别为E,F,这时,是否垂直于?
(3)如图③,为的平分线,当点G在线段的延长线上运动时,其他条件不变,这时,是否垂直于?
22.【学习新知】等边对等角是等腰三角形的性质定理,如图1,可以表述为
∵
∴
【新知应用】已知:在中,,若,则______;若,则______.
【尝试探究】如图2,四边形中,,,若连接,则平分.
某数学小组成员通过观察、实验,提出以下想法:延长到点,使得,连接,利用三角形全等的判定和等腰三角形的性质可以证明.请你参考他们的想法,写出完整的证明过程.
【拓展应用】借助上一问的尝试,继续探究:如图3所示,在五边形中,,,,连接,平分吗 请说明理由.
参考答案
1.解:等腰三角形的两边长分别为3和6,
当腰为3,底为6时,,不能构成三角形;
当腰为6,底为3时,能构成三角形,周长为,
故选:C.
2.解:周长相等的两个直角三角形不一定全等,故A选项不符合题意;
周长相等的两个钝角三角形不一定全等,故B选项不符合题意;
周长相等的两个等腰三角形不一定全等,故C选项不符合题意;
周长相等的两个等边三角形,三边对应相等,根据SSS可证这两个等边三角形全等,故D选项符合题意,
故选:D;
3.解:用反证法证明“三角形中最多有一个直角或钝角”,
第一步应假设三角形中至少有两个直角或钝角,
故选:B.
4.解:∵的垂直平分线分别交、于D、E,
∴,
∴,
∴,
∴,
∴,
∴;
故选D.
5.解: ,,,
,
,
,
,
,
故选:B.
6.解:由题意知,,,,
与全等,分两种情况求解:
①当时,,即,解得;
②当时,,即,解得,,即,解得;
综上所述,的值是1或,
故选:B.
7.解:连接并延长至D,如图,
∵点O是、的垂直平分线的交点,
∴,
∴,
∵是的一个外角,
∴,
同理,,
∴,
∴,
∴,
∵平分,平分,
∴,,
∴,
∴,
故选:C.
8.解:,
,,
中,与的平分线交于点,
,,
,,
,,
即和都是等腰三角形;
故①正确;
不一定等于,
不一定等于,
与不一定相等,
与不一定相等,故②错误.
在中,和的平分线相交于点,
,
,
;故③正确;
的周长为:;
故④正确;
故选:C.
9.解:∵,,
∴若用“”判断,可补充的条件是或;
故答案为:或.
10.解:由题意得是的垂直平分线,
,
,
的周长.
故答案为:11.
11.解:∵,,
∴,
∵是三角形的角平分线,
∴,
∵是三角形的高,
∴,
∴,
∴,
故答案为:.
12.解:如图,
,,
.
,
.
如图,,,
.
,
,
.
综上所述,这个等腰三角形顶角的度数为或.
故答案为:或
13.解:延长至,连接,
,
,
,即,
是等腰直角三角形,
,
∴,
故答案为:.
14.解:∵直线与x轴和y轴分别交与A、B两点,
当时,即,
解得:.
当时,,
∴.
∴.
∴.
∵,点C在射线上,
∴,即.
∵,
∴.
若以C、D、A为顶点的三角形与全等,则或,即或.
如图1所示,
当时,;
如图2所示,
当时,.
综上所述,的长为2或.
故答案为:2或.
15.解:是线段的垂直平分线,
与关于对称,
如图所示,连接,交于点,
,
,
周长,
当三点共线时,的周长最小,为的长,
为边的中点,,,
,,
,
,
周长,
周长的最小值为7,
故答案为:7.
16.解:如图作于E,于F.
∵,
∴,
∵,
∴,
∴,
∵OP平分∠AOB,PE⊥OA于E,PF⊥OB于F,
∴PE=PF,
在Rt△POE和Rt△POF中,
,
∴Rt△POE≌Rt△POF,
∴OE=OF,
在△PEM和△PFN中,
∴△PEM≌△PFN,
∴EM=NF,PM=PN,故(1)正确,
∴S△PEM=S△PNF,
∴S四边形PMON=S四边形PEOF=定值,故(3)正确,
∵,故(2)正确,
∵M,N的位置变化,∴MN的长度是变化的,故(4)错误.
故答案为:(1)(2)(3)
17.解:作于点D,如图所示,
∵是的外角平分线,,,
∴,
同理,
∴,又,,
∴平分,
∵,
∴.
18.(1)解:由三角形的三边关系可知:,
∵,
∴;
(2)解:延长至E,使,连接,
在中,∵,
∴,
∴,
由三角形的三边关系:,
∴,
∴.
19.(1)解:∵,
∴,
∵,
∴,
∴,
∵,,
∴;
∵,
∴,
∴;
(2)证明:由(1)得,
∴.
20.解:(1)①∵是边的垂直平分线,
∴,
∵是边的垂直平分线,
∴,
∴;
②∵是边的垂直平分线,
∴,
∵是边的垂直平分线,
∴,
∵,
∴;
(2),
,
,
,
.
21.(1)解:答案不唯一,如平分,
证明如下:
∵平分,
∴,
∵
∴
又,
∴,
∴
∴垂直于,即;
(2) ,理由如下:
∵平分,
∴,
∵
∴
又,
∴,
∴
∴垂直于,即;
(3) ,理由如下:
∵平分,
∴,
∵
∴
又,
∴,
∴
∴垂直于,即.
22.解:新知应用:
∵,
∴,
若,则;
若,则,
∴;
故答案是;
尝试探究:
证明:如图,延长到点,使得,连接,
∵,
又∵,
∴,
∵在和中,
,
∴,
∴,,
又∵,
∴,
∴,
即平分;
拓展应用:
证明:连接,延长到,使,连接,
∵,,
∴
∵在和中,
,
∴,
∴,,
又∵,,
∴
在和中,
,
∴,
∴,
∴,
即平分;
同课章节目录
