2023年中考数学三轮冲刺专题复习测试卷:二次函数的实际应用与几何问题(含答案)
文档属性
| 名称 | 2023年中考数学三轮冲刺专题复习测试卷:二次函数的实际应用与几何问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 385.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 10:39:50 | ||
图片预览


文档简介
2023年中考数学三轮冲刺专题复习测试卷:二次函数的实际应用与几何问题
一、单选题(共12题;共24分)
1.如图所示,将一根长 m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系 B.一次函数关系
C.二次函数关系 D.反比例函数关系
2.用一段 米长的铁丝在平地上围成一个长方形,求长方形的面积 (平方米)和长方形的一边的长 (米)的关系式为( )
A. B. C. D.
3.抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②﹣1<m<2;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为.其中正确的个数是( )
A.1 B.2 C.3 D.4
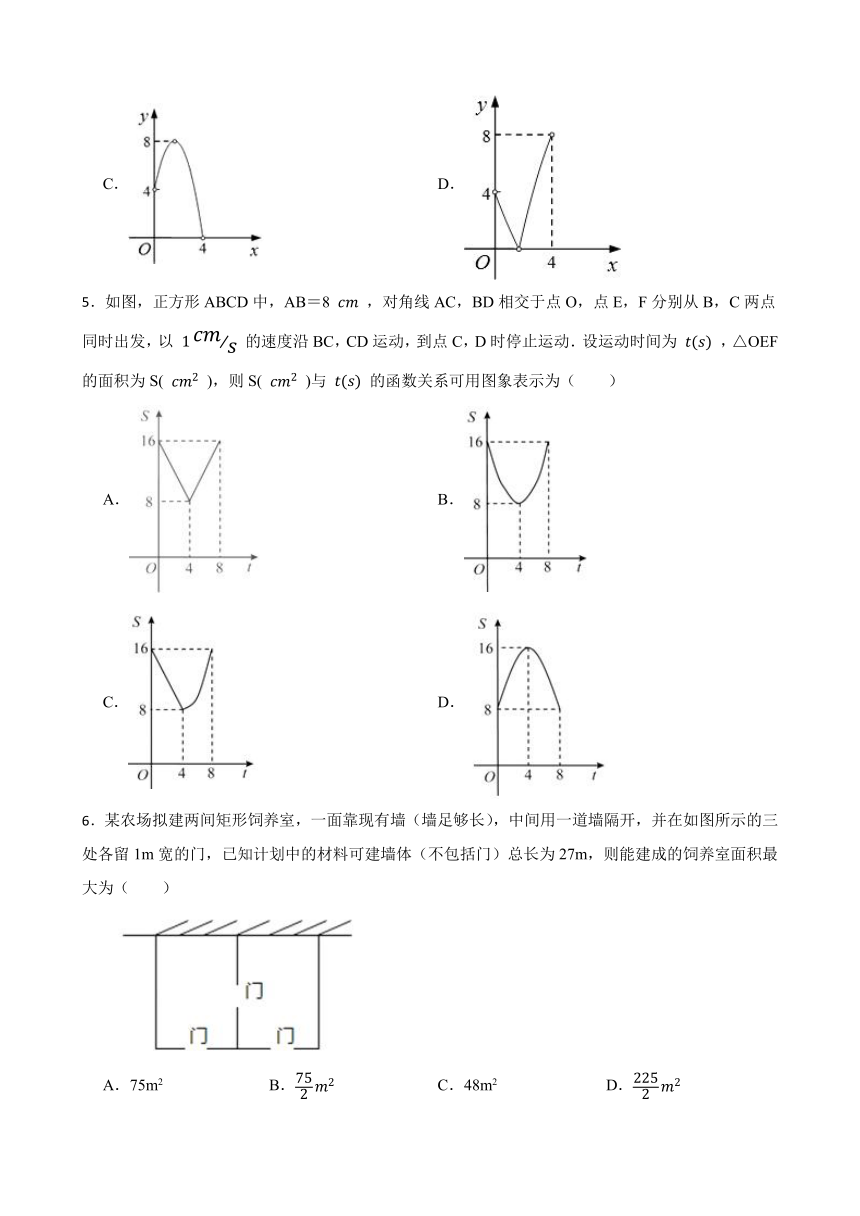
4.如图,半圆O的半径OA=4,P是OA延长线上一点,线段OP的垂直平分线分别交OP、半圆O于B、C两点,射线PC交半圆O于点D.设PA=x,CD=y,则能表示y与x的函数关系的图象是( )
A. B.
C. D.
5.如图,正方形ABCD中,AB=8 ,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以 的速度沿BC,CD运动,到点C,D时停止运动.设运动时间为 ,△OEF的面积为S( ),则S( )与 的函数关系可用图象表示为( )
A. B.
C. D.
6.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
A.75m2 B. C.48m2 D.
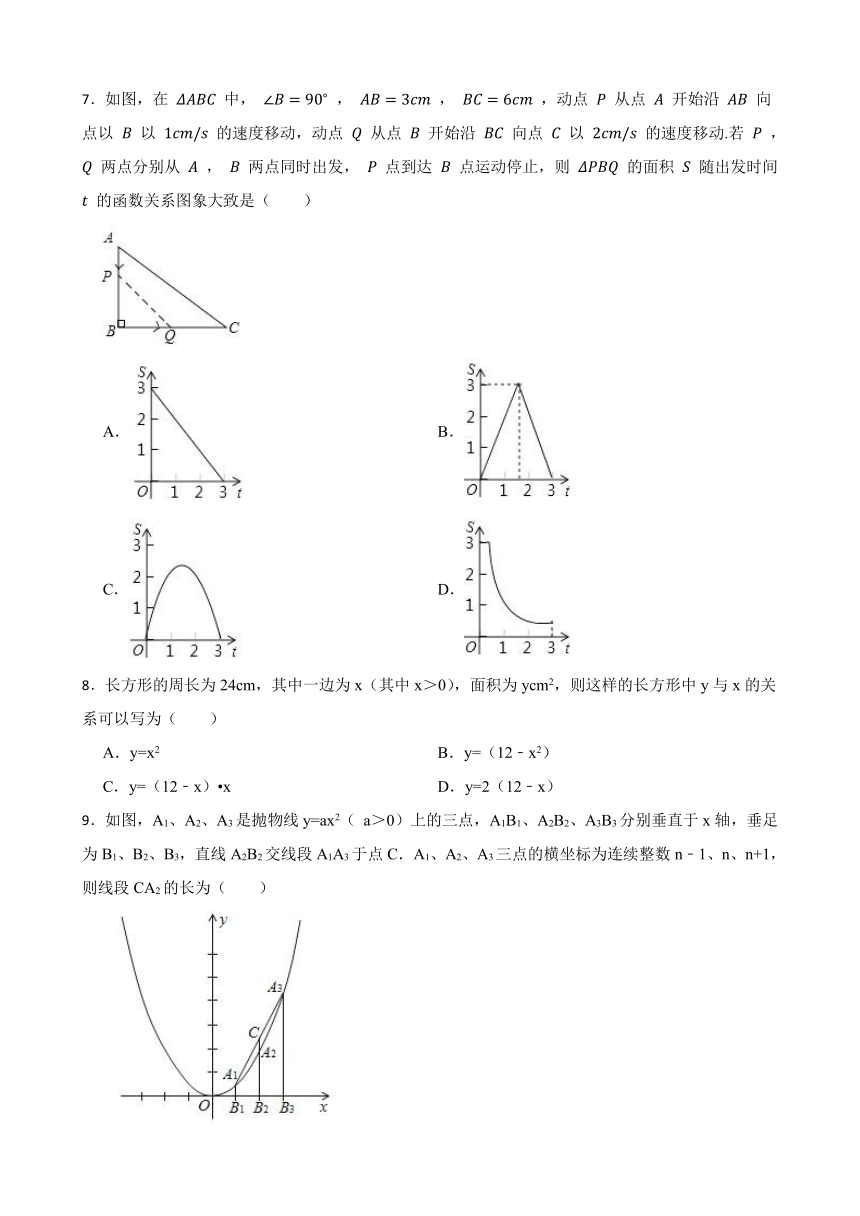
7.如图,在 中, , , ,动点 从点 开始沿 向点以 以 的速度移动,动点 从点 开始沿 向点 以 的速度移动.若 , 两点分别从 , 两点同时出发, 点到达 点运动停止,则 的面积 随出发时间 的函数关系图象大致是( )
A. B.
C. D.
8.长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=(12﹣x2)
C.y=(12﹣x) x D.y=2(12﹣x)
9.如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.A1、A2、A3三点的横坐标为连续整数n﹣1、n、n+1,则线段CA2的长为( )
A.a B.2a C.n D.n-1
10.在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,若a+b=5,则Rt△ABC的面积S关于边长c的函数关系式为( )
A.S= B.S= C.S= D.S=
11.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。设饲养室长为x(m),占地面积为y(m ),则y关于x的函数表达式是( )
A.y=-x +50x B.y= x +24x
C.y= x2+25x D.y= x2+26x
12.如图,抛物线y=﹣x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则 的值是( )
A. B. C. D.
二、填空题(共6题;共6分)
13.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的两处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为28m,则能建成的饲养室面积最大为 m2.
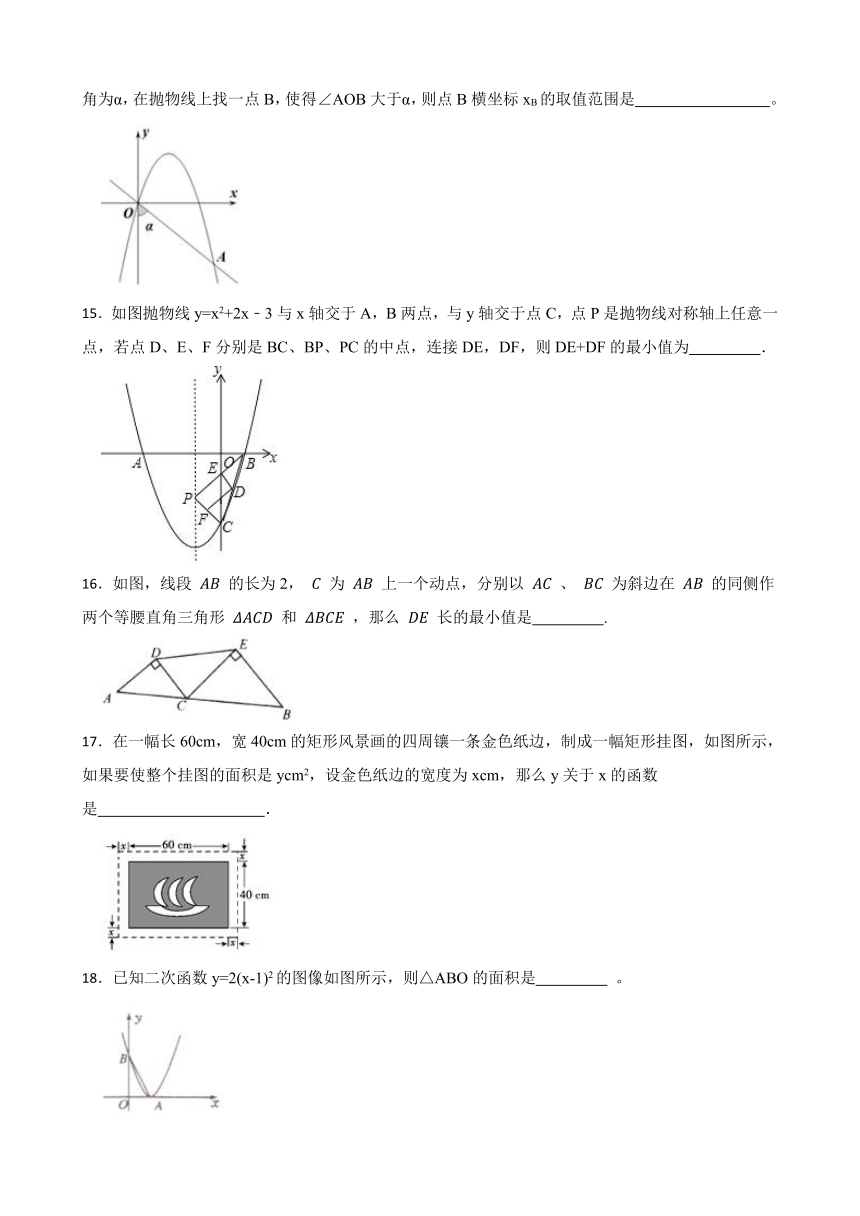
14.如图,点A在抛物线y= x2+3x上且横坐标为5,作直线OA,设直线OA与y轴负半轴的夹角为α,在抛物线上找一点B,使得∠AOB大于α,则点B横坐标xB的取值范围是 。
15.如图抛物线y=x2+2x﹣3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
16.如图,线段 的长为2, 为 上一个动点,分别以 、 为斜边在 的同侧作两个等腰直角三角形 和 ,那么 长的最小值是 .
17.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是ycm2,设金色纸边的宽度为xcm,那么y关于x的函数是 .
18.已知二次函数y=2(x-1)2的图像如图所示,则△ABO的面积是 。
三、综合题(共6题;共72分)
19.如图,抛物线y = x2 - bx + 3与x轴相交于点A,B,且过点C(4,3)
(1)求b的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P’,当四边形AP’PB为平行四边形时,求平移后抛物线的解析式
20.中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,下图是某跳台滑雪场地的截面示意图.平台长1米(即),平台距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系.已知滑道对应的函数为.运动员(看成点)在方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为l米,经实验表明:.
(1)求滑道对应的函数表达式;
(2)当时,通过计算判断运动员此时是否已落在滑道上;
(3)在某一次的试跳中,运动员甲从A处飞出,飞出的路径近似看作函数图象的一部分,根据实践可知,若运动员在飞行的过程中,存在飞行的高度与跳台滑道的垂直距离在米的范围内即可成功,请你通过计算说明该运动员此次试跳是否能成功.
21.小张准备进行如下实验操作:把一根长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形.
(1)要使这两个正方形的面积之和等于13cm2则这两个正方形的边长是多少?
(2)小张认为,这两个正方形的面积之和不可能等于11cm2你认为他的说法正确吗?请说明理由.
22.如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和木栏围成一个矩形花园 ,其中 ,已知矩形花园的一边靠墙,另三边一共用了50米木栏.
(1)若 ,所围成的矩形花园的面积为92平方米,求所利用旧墙 的长.
(2)求矩形花园 面积的最大值.
23.如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.
(1)当a=﹣1时,抛物线顶点D的坐标为 ,OE= ;
(2)OE的长是否与a值有关,说明你的理由;
(3)设∠DEO=β,45°≤β≤60°,求a的取值范围;
(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m的函数解析式及自变量m的取值范围.
24.如图,利用一面墙(墙的长度为12m),用22m长的篱笆,围成一个矩形场地.
(1)当BC是多少米时,场地的面积最大?
(2)若场地的面积为48m2,求BC的长.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】A
11.【答案】D
12.【答案】D
13.【答案】75
14.【答案】0<xB<
15.【答案】
16.【答案】1
17.【答案】y=(60+2x)(40+2x)
18.【答案】1
19.【答案】(1)解:∵ y = x2 - bx + 3,
∴3=42-4b+3,
解得:b=4,
∴y=x2 - 4x + 3
=(x-2)2-1,
∴P(2,-1);
(2)解:当y=0时,x2 - 4x + 3=0,
解得x1=1, x2=3,
∴AB=3-1=2,
∵ 四边形AP’PB为平行四边形 ,
∴PP'=AB=2,
∴P(0,-1),
∴抛物线的解析式为:y=x2-1.
20.【答案】(1)解:将代入得,,
∴,
∴;
(2)解:当时,,
∴,即,
当时,,
∴运动员没有落在滑道上;
(3)解:设飞行的高度与跳台滑道的垂直距离为,
∴
,
∵,
∴当时,存在飞行的高度与跳台滑道的垂直距离在米的范围内,
∴该运动员此次试跳能成功.
21.【答案】(1)解:设其中一个正方形的边长为xcm,则另一个正方形的边长为(5-x)cm,
依题意列方程得x2+(5-x)2=13,
整理得:x2-5x+6=0,
(x-2)(x-3)=0,
解方程得x1=2,x2=3,
因此这两个正方形的边长分别是2cm、3cm;
(2)解:两个正方形的面积之和不可能等于11cm2.理由:
设两个正方形的面积和为ycm2,则
y=x2+(5-x)2=2(x )2+ ,
∵a=2>0,
∴当x= 时,y的最小值=12.5>11,
∴两个正方形的面积之和不可能等于11cm2.
22.【答案】(1)解:设 ,则 ,且 ,
∴ ,
∵ ,
∴ ,即 ,解得:
又∵ ,
,即 的长为 ;
(2)解:由(1)可知: 且 ,
即: ,
∴当 且 时, ;
当 时, 时, .
23.【答案】(1)(﹣1,4);3
(2)解:结论:OE的长与a值无关.
理由:∵y=ax2+2ax﹣3a,
∴C(0,﹣3a),D(﹣1,﹣4a),
∴直线CD的解析式为y=ax﹣3a,
当y=0时,x=3,
∴E(3,0),
∴OE=3,
∴OE的长与a值无关
(3)解:当β=45°时,OC=OE=3,
∴﹣3a=3,
∴a=﹣1,
当β=60°时,在Rt△OCE中,OC= OE=3 ,
∴﹣3a=3 ,
∴a=﹣ ,
∴45°≤β≤60°,a的取值范围为﹣ ≤a≤﹣1
(4)解:如图,作PM⊥对称轴于M,PN⊥AB于N.
∵PD=PE,∠PMD=∠PNE=90°,∠DPE=∠MPN=90°,
∴∠DPM=∠EPN,
∴△DPM≌△EPN,
∴PM=PN,PM=EN,
∵D(﹣1,﹣4a),E(3,0),
∴EN=4+n=3﹣m,
∴n=﹣m﹣1,
当顶点D在对称轴上时,P(1,﹣2),此时m的值1,
∵抛物线的顶点在第二象限,
∴m<1.
∴n=﹣m﹣1(m<1)
24.【答案】(1)解:设BC=x米,场地的面积为y平方米,
由题意得,y=x =﹣ 2+11x=﹣ (x﹣11)2+60.5,
所以当BC=11米时,场地是面积最大是60.5平方米;
(2)解:当y=48时,
﹣ 2+11x=48,
解得x=6或16(舍),
答:BC的长是6米.
一、单选题(共12题;共24分)
1.如图所示,将一根长 m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A.正比例函数关系 B.一次函数关系
C.二次函数关系 D.反比例函数关系
2.用一段 米长的铁丝在平地上围成一个长方形,求长方形的面积 (平方米)和长方形的一边的长 (米)的关系式为( )
A. B. C. D.
3.抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②﹣1<m<2;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为.其中正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,半圆O的半径OA=4,P是OA延长线上一点,线段OP的垂直平分线分别交OP、半圆O于B、C两点,射线PC交半圆O于点D.设PA=x,CD=y,则能表示y与x的函数关系的图象是( )
A. B.
C. D.
5.如图,正方形ABCD中,AB=8 ,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以 的速度沿BC,CD运动,到点C,D时停止运动.设运动时间为 ,△OEF的面积为S( ),则S( )与 的函数关系可用图象表示为( )
A. B.
C. D.
6.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为( )
A.75m2 B. C.48m2 D.
7.如图,在 中, , , ,动点 从点 开始沿 向点以 以 的速度移动,动点 从点 开始沿 向点 以 的速度移动.若 , 两点分别从 , 两点同时出发, 点到达 点运动停止,则 的面积 随出发时间 的函数关系图象大致是( )
A. B.
C. D.
8.长方形的周长为24cm,其中一边为x(其中x>0),面积为ycm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=(12﹣x2)
C.y=(12﹣x) x D.y=2(12﹣x)
9.如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.A1、A2、A3三点的横坐标为连续整数n﹣1、n、n+1,则线段CA2的长为( )
A.a B.2a C.n D.n-1
10.在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,若a+b=5,则Rt△ABC的面积S关于边长c的函数关系式为( )
A.S= B.S= C.S= D.S=
11.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门。已知计划中的建筑材料可建围墙(不包括门)的总长度为50m。设饲养室长为x(m),占地面积为y(m ),则y关于x的函数表达式是( )
A.y=-x +50x B.y= x +24x
C.y= x2+25x D.y= x2+26x
12.如图,抛物线y=﹣x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则 的值是( )
A. B. C. D.
二、填空题(共6题;共6分)
13.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的两处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为28m,则能建成的饲养室面积最大为 m2.
14.如图,点A在抛物线y= x2+3x上且横坐标为5,作直线OA,设直线OA与y轴负半轴的夹角为α,在抛物线上找一点B,使得∠AOB大于α,则点B横坐标xB的取值范围是 。
15.如图抛物线y=x2+2x﹣3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
16.如图,线段 的长为2, 为 上一个动点,分别以 、 为斜边在 的同侧作两个等腰直角三角形 和 ,那么 长的最小值是 .
17.在一幅长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是ycm2,设金色纸边的宽度为xcm,那么y关于x的函数是 .
18.已知二次函数y=2(x-1)2的图像如图所示,则△ABO的面积是 。
三、综合题(共6题;共72分)
19.如图,抛物线y = x2 - bx + 3与x轴相交于点A,B,且过点C(4,3)
(1)求b的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P’,当四边形AP’PB为平行四边形时,求平移后抛物线的解析式
20.中国在2022年北京冬奥会上向全世界展示了“胸怀大局,自信开放,迎难而上,追求卓越,共创未来”的北京冬奥精神.跳台滑雪是北京冬奥会的比赛项目之一,下图是某跳台滑雪场地的截面示意图.平台长1米(即),平台距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系.已知滑道对应的函数为.运动员(看成点)在方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为l米,经实验表明:.
(1)求滑道对应的函数表达式;
(2)当时,通过计算判断运动员此时是否已落在滑道上;
(3)在某一次的试跳中,运动员甲从A处飞出,飞出的路径近似看作函数图象的一部分,根据实践可知,若运动员在飞行的过程中,存在飞行的高度与跳台滑道的垂直距离在米的范围内即可成功,请你通过计算说明该运动员此次试跳是否能成功.
21.小张准备进行如下实验操作:把一根长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形.
(1)要使这两个正方形的面积之和等于13cm2则这两个正方形的边长是多少?
(2)小张认为,这两个正方形的面积之和不可能等于11cm2你认为他的说法正确吗?请说明理由.
22.如图,在足够大的空地上有一段长为 米的旧墙 ,某人利用旧墙和木栏围成一个矩形花园 ,其中 ,已知矩形花园的一边靠墙,另三边一共用了50米木栏.
(1)若 ,所围成的矩形花园的面积为92平方米,求所利用旧墙 的长.
(2)求矩形花园 面积的最大值.
23.如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A,B两点,与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.
(1)当a=﹣1时,抛物线顶点D的坐标为 ,OE= ;
(2)OE的长是否与a值有关,说明你的理由;
(3)设∠DEO=β,45°≤β≤60°,求a的取值范围;
(4)以DE为斜边,在直线DE的左下方作等腰直角三角形PDE.设P(m,n),直接写出n关于m的函数解析式及自变量m的取值范围.
24.如图,利用一面墙(墙的长度为12m),用22m长的篱笆,围成一个矩形场地.
(1)当BC是多少米时,场地的面积最大?
(2)若场地的面积为48m2,求BC的长.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】A
11.【答案】D
12.【答案】D
13.【答案】75
14.【答案】0<xB<
15.【答案】
16.【答案】1
17.【答案】y=(60+2x)(40+2x)
18.【答案】1
19.【答案】(1)解:∵ y = x2 - bx + 3,
∴3=42-4b+3,
解得:b=4,
∴y=x2 - 4x + 3
=(x-2)2-1,
∴P(2,-1);
(2)解:当y=0时,x2 - 4x + 3=0,
解得x1=1, x2=3,
∴AB=3-1=2,
∵ 四边形AP’PB为平行四边形 ,
∴PP'=AB=2,
∴P(0,-1),
∴抛物线的解析式为:y=x2-1.
20.【答案】(1)解:将代入得,,
∴,
∴;
(2)解:当时,,
∴,即,
当时,,
∴运动员没有落在滑道上;
(3)解:设飞行的高度与跳台滑道的垂直距离为,
∴
,
∵,
∴当时,存在飞行的高度与跳台滑道的垂直距离在米的范围内,
∴该运动员此次试跳能成功.
21.【答案】(1)解:设其中一个正方形的边长为xcm,则另一个正方形的边长为(5-x)cm,
依题意列方程得x2+(5-x)2=13,
整理得:x2-5x+6=0,
(x-2)(x-3)=0,
解方程得x1=2,x2=3,
因此这两个正方形的边长分别是2cm、3cm;
(2)解:两个正方形的面积之和不可能等于11cm2.理由:
设两个正方形的面积和为ycm2,则
y=x2+(5-x)2=2(x )2+ ,
∵a=2>0,
∴当x= 时,y的最小值=12.5>11,
∴两个正方形的面积之和不可能等于11cm2.
22.【答案】(1)解:设 ,则 ,且 ,
∴ ,
∵ ,
∴ ,即 ,解得:
又∵ ,
,即 的长为 ;
(2)解:由(1)可知: 且 ,
即: ,
∴当 且 时, ;
当 时, 时, .
23.【答案】(1)(﹣1,4);3
(2)解:结论:OE的长与a值无关.
理由:∵y=ax2+2ax﹣3a,
∴C(0,﹣3a),D(﹣1,﹣4a),
∴直线CD的解析式为y=ax﹣3a,
当y=0时,x=3,
∴E(3,0),
∴OE=3,
∴OE的长与a值无关
(3)解:当β=45°时,OC=OE=3,
∴﹣3a=3,
∴a=﹣1,
当β=60°时,在Rt△OCE中,OC= OE=3 ,
∴﹣3a=3 ,
∴a=﹣ ,
∴45°≤β≤60°,a的取值范围为﹣ ≤a≤﹣1
(4)解:如图,作PM⊥对称轴于M,PN⊥AB于N.
∵PD=PE,∠PMD=∠PNE=90°,∠DPE=∠MPN=90°,
∴∠DPM=∠EPN,
∴△DPM≌△EPN,
∴PM=PN,PM=EN,
∵D(﹣1,﹣4a),E(3,0),
∴EN=4+n=3﹣m,
∴n=﹣m﹣1,
当顶点D在对称轴上时,P(1,﹣2),此时m的值1,
∵抛物线的顶点在第二象限,
∴m<1.
∴n=﹣m﹣1(m<1)
24.【答案】(1)解:设BC=x米,场地的面积为y平方米,
由题意得,y=x =﹣ 2+11x=﹣ (x﹣11)2+60.5,
所以当BC=11米时,场地是面积最大是60.5平方米;
(2)解:当y=48时,
﹣ 2+11x=48,
解得x=6或16(舍),
答:BC的长是6米.
同课章节目录
