湖北省黄石市黄石港区2022-2023学年九年级下学期6月月考数学试题(无答案)
文档属性
| 名称 | 湖北省黄石市黄石港区2022-2023学年九年级下学期6月月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 405.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-22 22:32:59 | ||
图片预览

文档简介
九年级数学模拟试卷
满分:120分 时间:120分钟
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.若a-|a|=-20,则实数a在数轴上的对应点一定在( )
A.原点左侧 B.原点或原点左侧 C.原点右侧 D.原点或原点右侧
2.如图是四届冬奥会会标的一部分,其中是轴对称图形的是( )
A. B. C. D.
3.如图是由几个小立方块所搭成的几何体从上面所看到的,小正方形中的数字表示在该方块的个数,则从左边看到的这个几何体的形状图为( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.函数中自变量x的取值范围是( )
A.x≥-2 B.x>-2 C.x>-2且x≠-1 D.x≥-2且x≠-1
6.为激励青少年爱读书、读好书、善读书,某校积极开展全员阅读活动.小吴为了了解本班同学一月的课外阅读量,随机选取班上部分同学进行调查,并将调查结果绘制成折线统计图(如图)下列说法中,正确的是( )
A.随机选取了14名同学 B.中位数是2本 C.众数是4本 D.平均数是2.4本
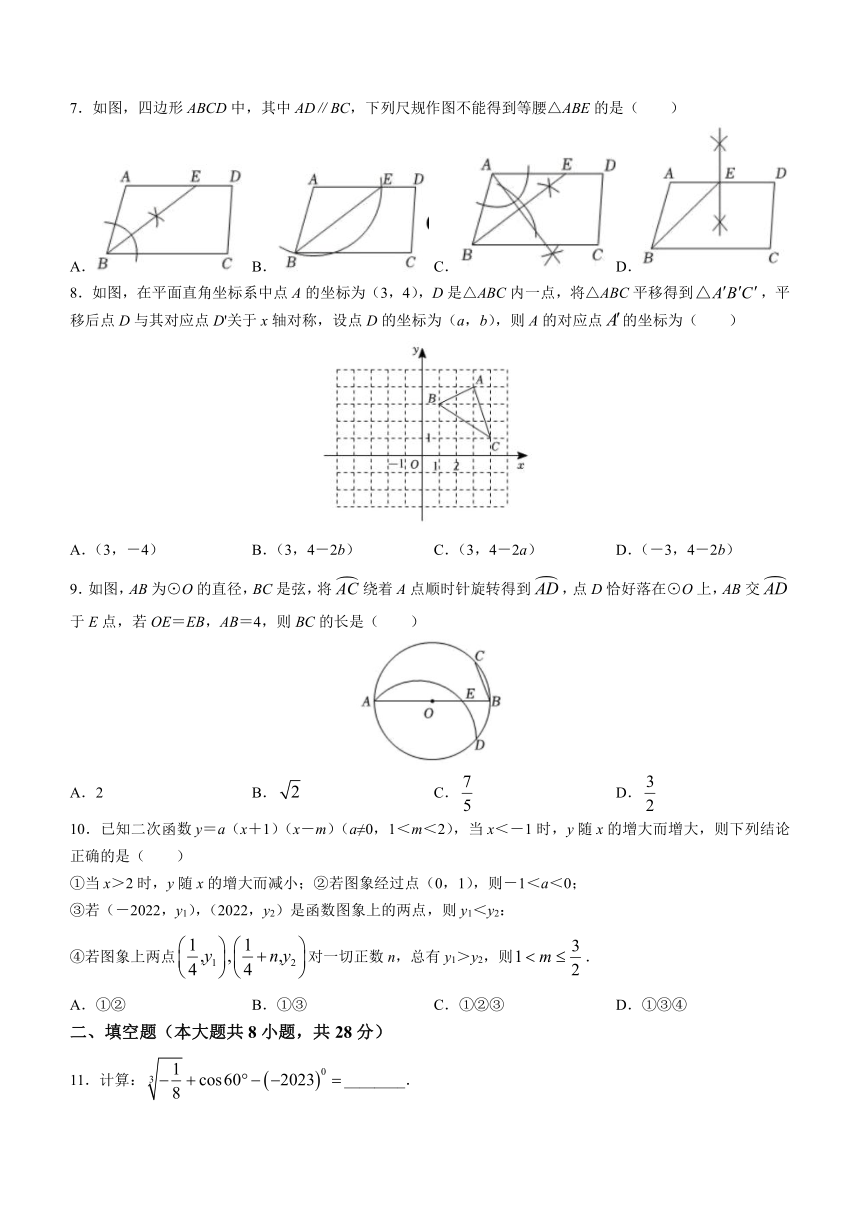
7.如图,四边形ABCD中,其中AD∥BC,下列尺规作图不能得到等腰△ABE的是( )
A. B. C. D.
8.如图,在平面直角坐标系中点A的坐标为(3,4),D是△ABC内一点,将△ABC平移得到,平移后点D与其对应点D'关于x轴对称,设点D的坐标为(a,b),则A的对应点的坐标为( )
A.(3,-4) B.(3,4-2b) C.(3,4-2a) D.(-3,4-2b)
9.如图,AB为⊙O的直径,BC是弦,将绕着A点顺时针旋转得到,点D恰好落在⊙O上,AB交于E点,若OE=EB,AB=4,则BC的长是( )
A.2 B. C. D.
10.已知二次函数y=a(x+1)(x-m)(a≠0,1<m<2),当x<-1时,y随x的增大而增大,则下列结论正确的是( )
①当x>2时,y随x的增大而减小;②若图象经过点(0,1),则-1<a<0;
③若(-2022,y1),(2022,y2)是函数图象上的两点,则y1<y2:
④若图象上两点对一切正数n,总有y1>y2,则.
A.①② B.①③ C.①②③ D.①③④
二、填空题(本大题共8小题,共28分)
11.计算:________.
12.因式分解:2ax2-4axy+2ay2=________.
13.文化和旅游部3日公布:2023年“五一”假期全国国内旅游出游合计约274000000人次,274000000用科学记数法表示是________.
14.如图,扇形纸片AOB的半径为4,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为________.
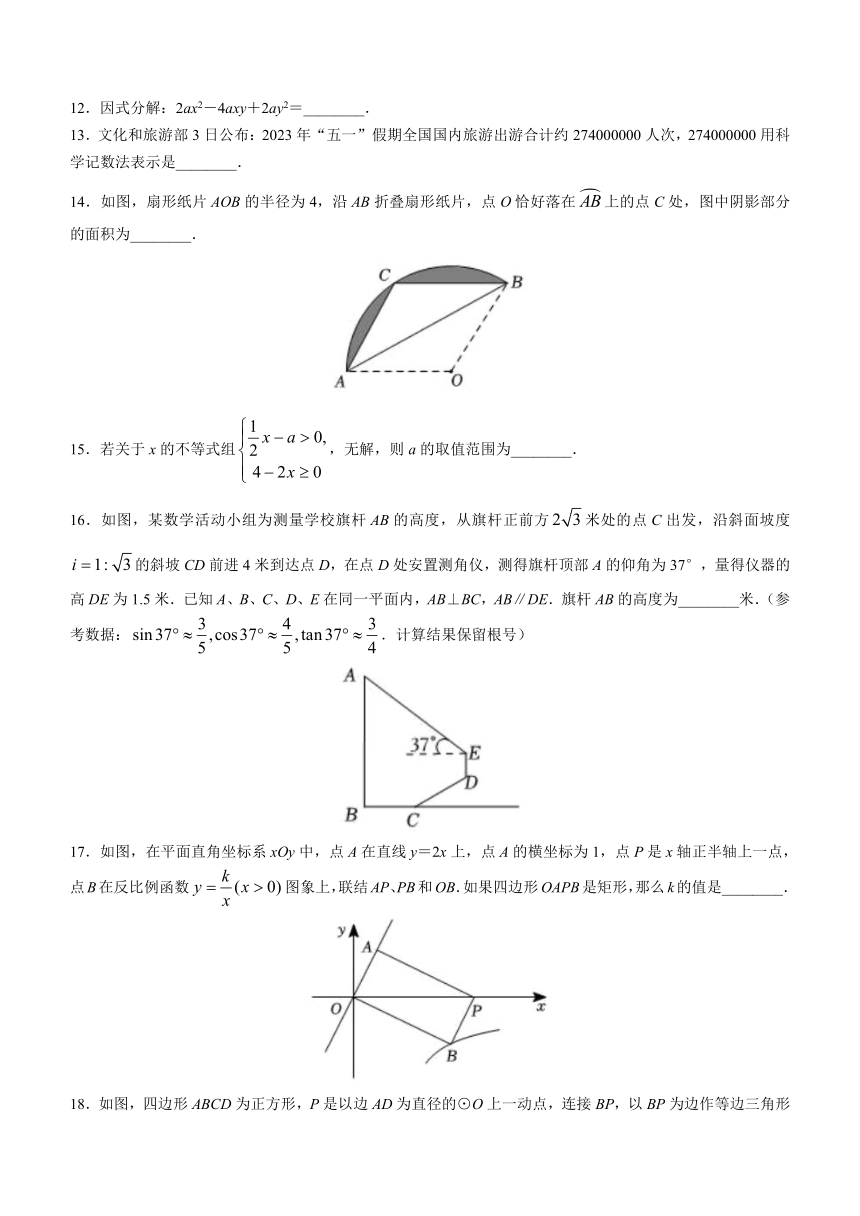
15.若关于x的不等式组,无解,则a的取值范围为________.
16.如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方米处的点C出发,沿斜面坡度的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.旗杆AB的高度为________米.(参考数据:.计算结果保留根号)
17.如图,在平面直角坐标系xOy中,点A在直线y=2x上,点A的横坐标为1,点P是x轴正半轴上一点,点B在反比例函数图象上,联结AP、PB和OB.如果四边形OAPB是矩形,那么k的值是________.
18.如图,四边形ABCD为正方形,P是以边AD为直径的⊙O上一动点,连接BP,以BP为边作等边三角形BPQ,连接OQ,若AB=2,则线段OQ的最大值为________.
三、解答题(本大题共7小题,共62分。解答应写出文字说明,证明过程或演算步骤)
19.(本小题7分)请你先化简,再从-2,2,中选择一个合适的数代入求值.
20.(本小题8.0分)如图,AD,BC交于点E,AC=BD,∠C=∠D=90°.
(1)求证:△ACE≌△BDE;
(2)若∠CAE=26°,求∠ABC的度数.
21.(本小题8分)为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2<t<3,C:3<t<4,D:t>4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取________人,条形统计图中的m=________;
(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
22.(本小题8分)阅读材料,解答问题:材料1为了解方程(x2)2-13x2+36=0,如果我们把x2看作一个整体,然后设y=x2,则原方程可化为y2-13y+36=0,经过运算,原方程的解为,.我们把以上这种解决问题的方法通常叫做换元法.
材料2 已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:(1)直接应用:解方程:x4-x2-6=0.
(2)间接应用:已知实数m,n满足:m2-7m+2=0,n2-7n+2=0,求的值.
(3)拓展应用:已知实数x,y满足:,求的值.
23.(本小题9分)一大型商场经营某种品牌商品,该商品的进价为每件30元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件) 40 50 60
y(件) 10000 9500 9000
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于150元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于150元/件时,每销售一件商品便向某慈善机构捐赠m元(10≤m≤60),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请求出m的取值范围.
24.(本小题10分)如图,AB为⊙O的直径,C、D为圆上两点,∠ABD=2∠BAC,CE⊥BD于点.
(1)求证:E是⊙O的切线;
(2)若C=3,D=7,求线段E的长:
(3)在(2)的条件下,求cos∠DCA的值.
25.如图,已知抛物线交x轴于A(-3,0),B(4,0)两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.
(1)求抛物线的表达式;
(2)连接OP,BP,若,求点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.
满分:120分 时间:120分钟
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1.若a-|a|=-20,则实数a在数轴上的对应点一定在( )
A.原点左侧 B.原点或原点左侧 C.原点右侧 D.原点或原点右侧
2.如图是四届冬奥会会标的一部分,其中是轴对称图形的是( )
A. B. C. D.
3.如图是由几个小立方块所搭成的几何体从上面所看到的,小正方形中的数字表示在该方块的个数,则从左边看到的这个几何体的形状图为( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.函数中自变量x的取值范围是( )
A.x≥-2 B.x>-2 C.x>-2且x≠-1 D.x≥-2且x≠-1
6.为激励青少年爱读书、读好书、善读书,某校积极开展全员阅读活动.小吴为了了解本班同学一月的课外阅读量,随机选取班上部分同学进行调查,并将调查结果绘制成折线统计图(如图)下列说法中,正确的是( )
A.随机选取了14名同学 B.中位数是2本 C.众数是4本 D.平均数是2.4本
7.如图,四边形ABCD中,其中AD∥BC,下列尺规作图不能得到等腰△ABE的是( )
A. B. C. D.
8.如图,在平面直角坐标系中点A的坐标为(3,4),D是△ABC内一点,将△ABC平移得到,平移后点D与其对应点D'关于x轴对称,设点D的坐标为(a,b),则A的对应点的坐标为( )
A.(3,-4) B.(3,4-2b) C.(3,4-2a) D.(-3,4-2b)
9.如图,AB为⊙O的直径,BC是弦,将绕着A点顺时针旋转得到,点D恰好落在⊙O上,AB交于E点,若OE=EB,AB=4,则BC的长是( )
A.2 B. C. D.
10.已知二次函数y=a(x+1)(x-m)(a≠0,1<m<2),当x<-1时,y随x的增大而增大,则下列结论正确的是( )
①当x>2时,y随x的增大而减小;②若图象经过点(0,1),则-1<a<0;
③若(-2022,y1),(2022,y2)是函数图象上的两点,则y1<y2:
④若图象上两点对一切正数n,总有y1>y2,则.
A.①② B.①③ C.①②③ D.①③④
二、填空题(本大题共8小题,共28分)
11.计算:________.
12.因式分解:2ax2-4axy+2ay2=________.
13.文化和旅游部3日公布:2023年“五一”假期全国国内旅游出游合计约274000000人次,274000000用科学记数法表示是________.
14.如图,扇形纸片AOB的半径为4,沿AB折叠扇形纸片,点O恰好落在上的点C处,图中阴影部分的面积为________.
15.若关于x的不等式组,无解,则a的取值范围为________.
16.如图,某数学活动小组为测量学校旗杆AB的高度,从旗杆正前方米处的点C出发,沿斜面坡度的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.旗杆AB的高度为________米.(参考数据:.计算结果保留根号)
17.如图,在平面直角坐标系xOy中,点A在直线y=2x上,点A的横坐标为1,点P是x轴正半轴上一点,点B在反比例函数图象上,联结AP、PB和OB.如果四边形OAPB是矩形,那么k的值是________.
18.如图,四边形ABCD为正方形,P是以边AD为直径的⊙O上一动点,连接BP,以BP为边作等边三角形BPQ,连接OQ,若AB=2,则线段OQ的最大值为________.
三、解答题(本大题共7小题,共62分。解答应写出文字说明,证明过程或演算步骤)
19.(本小题7分)请你先化简,再从-2,2,中选择一个合适的数代入求值.
20.(本小题8.0分)如图,AD,BC交于点E,AC=BD,∠C=∠D=90°.
(1)求证:△ACE≌△BDE;
(2)若∠CAE=26°,求∠ABC的度数.
21.(本小题8分)为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2<t<3,C:3<t<4,D:t>4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取________人,条形统计图中的m=________;
(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
22.(本小题8分)阅读材料,解答问题:材料1为了解方程(x2)2-13x2+36=0,如果我们把x2看作一个整体,然后设y=x2,则原方程可化为y2-13y+36=0,经过运算,原方程的解为,.我们把以上这种解决问题的方法通常叫做换元法.
材料2 已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,显然m,n是方程x2-x-1=0的两个不相等的实数根,由韦达定理可知m+n=1,mn=-1.
根据上述材料,解决以下问题:(1)直接应用:解方程:x4-x2-6=0.
(2)间接应用:已知实数m,n满足:m2-7m+2=0,n2-7n+2=0,求的值.
(3)拓展应用:已知实数x,y满足:,求的值.
23.(本小题9分)一大型商场经营某种品牌商品,该商品的进价为每件30元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元/件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:
x(元/件) 40 50 60
y(件) 10000 9500 9000
(1)求y与x的函数关系式(不求自变量的取值范围);
(2)在销售过程中要求销售单价不低于成本价,且不高于150元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?
(3)抗疫期间,该商场这种商品售价不大于150元/件时,每销售一件商品便向某慈善机构捐赠m元(10≤m≤60),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请求出m的取值范围.
24.(本小题10分)如图,AB为⊙O的直径,C、D为圆上两点,∠ABD=2∠BAC,CE⊥BD于点.
(1)求证:E是⊙O的切线;
(2)若C=3,D=7,求线段E的长:
(3)在(2)的条件下,求cos∠DCA的值.
25.如图,已知抛物线交x轴于A(-3,0),B(4,0)两点,交y轴于点C,点P是抛物线上一点,连接AC、BC.
(1)求抛物线的表达式;
(2)连接OP,BP,若,求点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使得∠QBA=75°?若存在,直接写出点Q的坐标;若不存在,请说明理由.
同课章节目录
