冀教版数学九年级下册 29.2 直线与圆的位置关系 教案
文档属性
| 名称 | 冀教版数学九年级下册 29.2 直线与圆的位置关系 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 660.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-21 00:00:00 | ||
图片预览



文档简介
课题:冀教版九年级下册
《29.2.直线与圆的位置关系》教学设计
一、教材分析:
1、 教材的地位和作用
圆的有关性质,被广泛地应用于工农业生产、交通运输等方面,所涉及的数学知识较为广泛;学好本章内容,能提高解题的综合能力。而本节的内容紧接点与圆的位置关系,它体现了运动的观点,是研究有关性质的基础,也为后面学习圆与圆的位置关系及高中继续学习几何知识作铺垫。
2、 教学目标
1、理解直线和圆相交、相切、相离等概念;
2、理解直线和圆相交、相切、相离的判定方法和性质.
3、 教学重、难点
重点:理解直线与圆的相交、相离、相切三种位置关系;
难点:学生能根据圆心到直线的距离d与圆的半径r之间的数量关系,揭示直线与圆的位置关系;直线与圆的三种位置关系判定方法的运用。
教学软件:
希沃白板5,geogebra动态几何软件,班级优化大师、希沃授课助手
四、教学过程
(一)回顾复习、引入新课
1、教师借助希沃白板5,随机拖动点A,学生回顾上节课的内容点与圆的位置关系。教师提问:若将点改为直线,那么直线与圆的位置关系又如何?引入新课。
2.播放海上日出这一自然景观的视频,
教师提问:从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
你发现这个自然现象反映出直线和圆的公共点个数有几种情况?
小组活动1:合作探究用圆规和直尺将这几种情况在学案中画出来
教师借助班级优化大师选择学生,利用希沃授课助手拍照上传,展示学生的探究成果,教师点评加分。
(通过直观画面展示问题情景,学生大胆猜想,激发学生学习兴趣,营造探索问题的氛围。)
(二)自学指导,探索新知
探究1 借助希沃白板5展示以下内容:
小组活动2:阅读课本内容,并用双色笔对重要内容做上记号,根据学案模板自学,完成三种情况的定义
填空:
位置关系: 位置关系: 位置关系:
公共点个数: 公共点个数: 公共点个数:
共同点名称: 共同点名称: 共同点名称:
直线名称: 直线名称: 直线名称:
利用班优抽取一个小组,小徐选派三个代表,分别对三种位置关系进行定义。
教师进行点评并总结:圆与直线的位置关系可用公共点的个数进行判定(定义法),反之由点到直线的位置关系可知公共点的个数,教师进行板书:
希沃白板5课堂活动知识配对:用定义判断直线和圆的位置关系
生活中的3个例子分别是:相交、相离、相切
(通过课堂活动同时让学生体会到数学知识无处不在,应用数学无处不有。符合“数学教学应从生活经验出发”的新课程标准要求。)
探究2
教师提问:上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?我们曾经用数量关系来判别点和圆的位置关系。类似地,能否用数量关系来判别直线与圆的位置关系呢?
师生一起回顾点到直线的距离这一知识点
小组活动3根据圆心到直线的距离d与半径r之间的数量关系是否能揭示直线和圆的位置关系是相交、相切、相离?
小组成员进行交流互动,并完成学案上的填空任务:
通过测量自己前面所画的圆的半径 r与该圆圆心到直线的距离d,并比较d与 r的大小关系
d= r = d= r= d= r =
d r d r d r
教师利用班级优化大师选派一个组的两个代表上希沃白板5的利用克隆功能拖出三个圆,用白板中的三角尺功能进行测量,比较圆心到直线的距离d与半径r的大小关系。
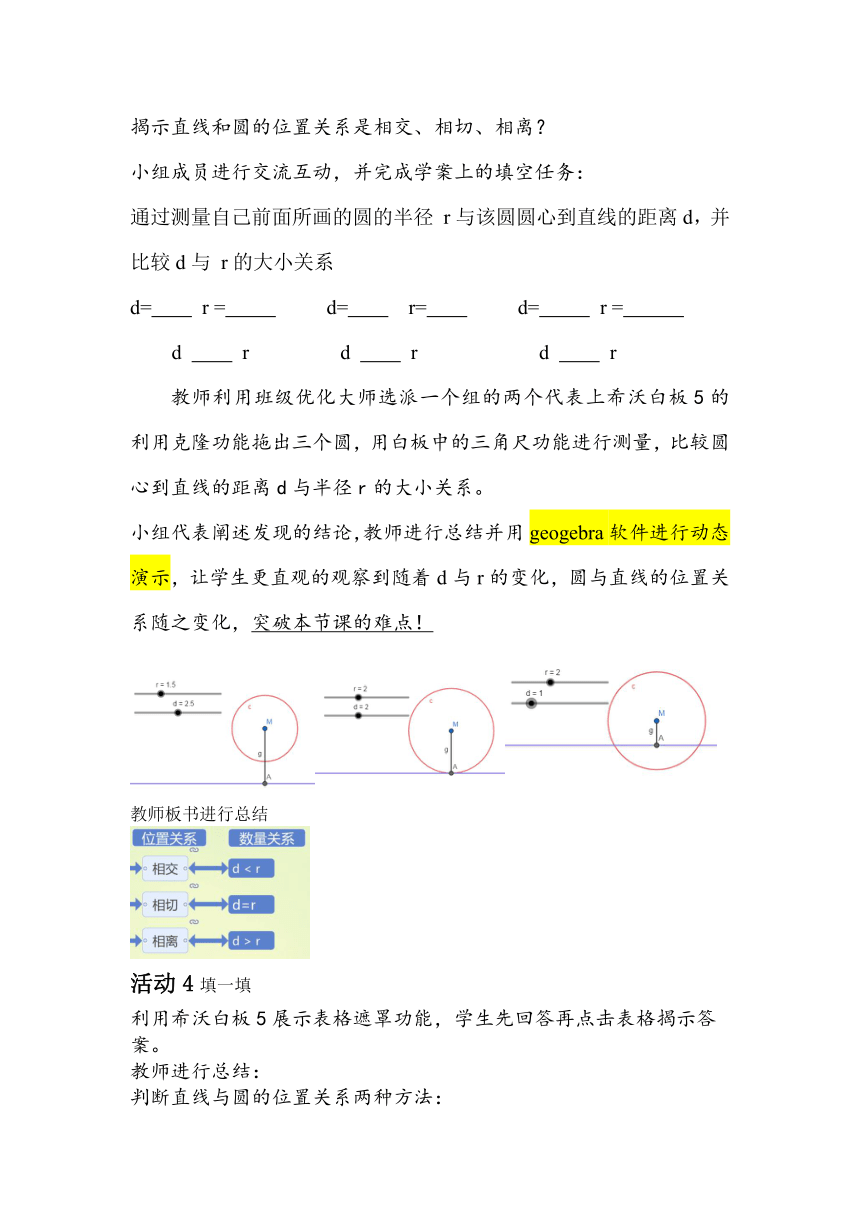
小组代表阐述发现的结论,教师进行总结并用geogebra软件进行动态演示,让学生更直观的观察到随着d与r的变化,圆与直线的位置关系随之变化,突破本节课的难点!
教师板书进行总结
活动4填一填
利用希沃白板5展示表格遮罩功能,学生先回答再点击表格揭示答案。
教师进行总结:
判断直线与圆的位置关系两种方法:
定义法(公共点的个数)
d与r的数量关系法
总结:位置关系、数量关系、公共点的个数这三者可知一推二
(三)小试牛刀
练习1 已知圆的直径为13cm,设直线和圆心的距离为d :
1)若d=4.5cm ,则直线与圆 , 直线与圆有 个公共点.
2)若d=6.5cm ,则直线与圆 , 直线与圆有 个公共点.
3)若d= 8 cm ,则直线与圆 , 直线与圆有 个公共点.
练习2 已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交, 则 .
游戏PK:利用希沃白板5中分组竞争这一课堂活动环节活跃课堂氛围,巩固位置关系等价于d、r的数量关系是什么
(四)巩固提高
例1:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
r=2cm;
r=2.4cm
r=3cm.
小组活动3完成变式训练
变式:在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,
以C为圆心,r为半径作圆。
①当r满足 时,直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
④当r满足 时, 线段AB与⊙C只有一个公共点。
先学生小组合作探究,之后教师借助geogebra软件进行动态演示,帮助学生理解在r在什么取值范围内圆与直线的位置关系是相交、相离、相切。
(四)小结新知,画龙点睛
1. 直线与圆有三种位置关系: 相离 、 相切 、 相交 。
2.识别直线和圆的位置关系的方法:
数学思想:
教案设计说明:
(1)本节课的设计体现了“学会学习,为终身学习作准备”的理念,让学生在“数学活动”中获得学习的方法、能力和数学的思想,同时获得对数学学习的积极情感。
(2)教师是教学工作的服务者,教师的责任是为学生的发展创造一个和谐、开放、富有情趣的学习新知识的探究氛围。本课引用海上日出这一美伦美奂的景色,营造了探索问题的氛围;例题和提高练习的选用,让学生体会到数学知识无处不在,应用数学无处不有,让学生感受到“生活处处不数学”,从而在生活中主动发觉问题加以解决,达到“乐学”的目的;把实际问题与数学知识紧密联系,逐步渗透数学建模的思想方法,让学生掌握到更多的技能技巧。
(3)课前设问,呈现本课知识目标。课前的3个设问,直奔主题,学生对本课应掌握的知识一目了然,重点分明。
(4)变式训练,把学生置于创新思维的深入培养过程之中。众所周知,实施素质教育的突破口是创新教育,要培养学生的创新能力,就要有让学生进行创新思维的问题,而变式训练就是让学生展开创新思维的主阵地。教师在教学活动中应努力的去挖掘教材,有意识的去训练学生的思维,从而使学生逐渐形成良好的个性思维品质和良好的数学学习习惯。
没有公共点
一个公共点
两个公共点
l
O
l
O
A
l
O
A
B
d
r
d
r
d
r
d >r
d =r
d <r
直线 l 和⊙O 相离
直线 l 和⊙O 相切
直线 l 和⊙O 相交
《29.2.直线与圆的位置关系》教学设计
一、教材分析:
1、 教材的地位和作用
圆的有关性质,被广泛地应用于工农业生产、交通运输等方面,所涉及的数学知识较为广泛;学好本章内容,能提高解题的综合能力。而本节的内容紧接点与圆的位置关系,它体现了运动的观点,是研究有关性质的基础,也为后面学习圆与圆的位置关系及高中继续学习几何知识作铺垫。
2、 教学目标
1、理解直线和圆相交、相切、相离等概念;
2、理解直线和圆相交、相切、相离的判定方法和性质.
3、 教学重、难点
重点:理解直线与圆的相交、相离、相切三种位置关系;
难点:学生能根据圆心到直线的距离d与圆的半径r之间的数量关系,揭示直线与圆的位置关系;直线与圆的三种位置关系判定方法的运用。
教学软件:
希沃白板5,geogebra动态几何软件,班级优化大师、希沃授课助手
四、教学过程
(一)回顾复习、引入新课
1、教师借助希沃白板5,随机拖动点A,学生回顾上节课的内容点与圆的位置关系。教师提问:若将点改为直线,那么直线与圆的位置关系又如何?引入新课。
2.播放海上日出这一自然景观的视频,
教师提问:从海上日出这种自然现象中可以抽象出哪些基本的几何图形呢?
你发现这个自然现象反映出直线和圆的公共点个数有几种情况?
小组活动1:合作探究用圆规和直尺将这几种情况在学案中画出来
教师借助班级优化大师选择学生,利用希沃授课助手拍照上传,展示学生的探究成果,教师点评加分。
(通过直观画面展示问题情景,学生大胆猜想,激发学生学习兴趣,营造探索问题的氛围。)
(二)自学指导,探索新知
探究1 借助希沃白板5展示以下内容:
小组活动2:阅读课本内容,并用双色笔对重要内容做上记号,根据学案模板自学,完成三种情况的定义
填空:
位置关系: 位置关系: 位置关系:
公共点个数: 公共点个数: 公共点个数:
共同点名称: 共同点名称: 共同点名称:
直线名称: 直线名称: 直线名称:
利用班优抽取一个小组,小徐选派三个代表,分别对三种位置关系进行定义。
教师进行点评并总结:圆与直线的位置关系可用公共点的个数进行判定(定义法),反之由点到直线的位置关系可知公共点的个数,教师进行板书:
希沃白板5课堂活动知识配对:用定义判断直线和圆的位置关系
生活中的3个例子分别是:相交、相离、相切
(通过课堂活动同时让学生体会到数学知识无处不在,应用数学无处不有。符合“数学教学应从生活经验出发”的新课程标准要求。)
探究2
教师提问:上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?我们曾经用数量关系来判别点和圆的位置关系。类似地,能否用数量关系来判别直线与圆的位置关系呢?
师生一起回顾点到直线的距离这一知识点
小组活动3根据圆心到直线的距离d与半径r之间的数量关系是否能揭示直线和圆的位置关系是相交、相切、相离?
小组成员进行交流互动,并完成学案上的填空任务:
通过测量自己前面所画的圆的半径 r与该圆圆心到直线的距离d,并比较d与 r的大小关系
d= r = d= r= d= r =
d r d r d r
教师利用班级优化大师选派一个组的两个代表上希沃白板5的利用克隆功能拖出三个圆,用白板中的三角尺功能进行测量,比较圆心到直线的距离d与半径r的大小关系。
小组代表阐述发现的结论,教师进行总结并用geogebra软件进行动态演示,让学生更直观的观察到随着d与r的变化,圆与直线的位置关系随之变化,突破本节课的难点!
教师板书进行总结
活动4填一填
利用希沃白板5展示表格遮罩功能,学生先回答再点击表格揭示答案。
教师进行总结:
判断直线与圆的位置关系两种方法:
定义法(公共点的个数)
d与r的数量关系法
总结:位置关系、数量关系、公共点的个数这三者可知一推二
(三)小试牛刀
练习1 已知圆的直径为13cm,设直线和圆心的距离为d :
1)若d=4.5cm ,则直线与圆 , 直线与圆有 个公共点.
2)若d=6.5cm ,则直线与圆 , 直线与圆有 个公共点.
3)若d= 8 cm ,则直线与圆 , 直线与圆有 个公共点.
练习2 已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交, 则 .
游戏PK:利用希沃白板5中分组竞争这一课堂活动环节活跃课堂氛围,巩固位置关系等价于d、r的数量关系是什么
(四)巩固提高
例1:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
r=2cm;
r=2.4cm
r=3cm.
小组活动3完成变式训练
变式:在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm,
以C为圆心,r为半径作圆。
①当r满足 时,直线AB与⊙C相离。
②当r满足 时,直线AB与⊙C相切。
③当r满足 时,直线AB与⊙C相交。
④当r满足 时, 线段AB与⊙C只有一个公共点。
先学生小组合作探究,之后教师借助geogebra软件进行动态演示,帮助学生理解在r在什么取值范围内圆与直线的位置关系是相交、相离、相切。
(四)小结新知,画龙点睛
1. 直线与圆有三种位置关系: 相离 、 相切 、 相交 。
2.识别直线和圆的位置关系的方法:
数学思想:
教案设计说明:
(1)本节课的设计体现了“学会学习,为终身学习作准备”的理念,让学生在“数学活动”中获得学习的方法、能力和数学的思想,同时获得对数学学习的积极情感。
(2)教师是教学工作的服务者,教师的责任是为学生的发展创造一个和谐、开放、富有情趣的学习新知识的探究氛围。本课引用海上日出这一美伦美奂的景色,营造了探索问题的氛围;例题和提高练习的选用,让学生体会到数学知识无处不在,应用数学无处不有,让学生感受到“生活处处不数学”,从而在生活中主动发觉问题加以解决,达到“乐学”的目的;把实际问题与数学知识紧密联系,逐步渗透数学建模的思想方法,让学生掌握到更多的技能技巧。
(3)课前设问,呈现本课知识目标。课前的3个设问,直奔主题,学生对本课应掌握的知识一目了然,重点分明。
(4)变式训练,把学生置于创新思维的深入培养过程之中。众所周知,实施素质教育的突破口是创新教育,要培养学生的创新能力,就要有让学生进行创新思维的问题,而变式训练就是让学生展开创新思维的主阵地。教师在教学活动中应努力的去挖掘教材,有意识的去训练学生的思维,从而使学生逐渐形成良好的个性思维品质和良好的数学学习习惯。
没有公共点
一个公共点
两个公共点
l
O
l
O
A
l
O
A
B
d
r
d
r
d
r
d >r
d =r
d <r
直线 l 和⊙O 相离
直线 l 和⊙O 相切
直线 l 和⊙O 相交
