2022-2023学年湘教版八年级下册数学期末复习试卷(无答案)
文档属性
| 名称 | 2022-2023学年湘教版八年级下册数学期末复习试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 216.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-23 00:21:25 | ||
图片预览

文档简介
湘教版八年级下数学期末复习试卷
一、选择题
1. 对于任意的矩形,下列说法一定正确的是( )
A. 对角线垂直且相等 B. 四边都互相垂直
C. 四个角都相等 D. 是轴对称图形,但不是中心对称图形
2. 在平面直角坐标系中,点向右平移个单位长度,得到点,则点的坐标为( )
A. B. C. D.
3. 函数是关于的一次函数,则,的值为( )
A. , B. , C. , D. ,
4. 某校有名学生参加体育测试,其成绩在分之间的有人,则在分之间的频率是( )
A. B. C. D.
5. 将直线向上平移个单位长度后,所得的直线的解析式为( )
A. B. C. D.
6. 下列说法中,正确的有( )
都含有的两个直角三角形一定全等;
都含有的两个等腰三角形一定全等;
底边相等的两个等腰三角形一定全等;
边长都为的两个等边三角形一定全等;
如果两个等腰三角形的腰长相等,且一腰上的高与另一腰的夹角也恰好相等,那么这两个等腰三角形全等.
A. 个 B. 个 C. 个 D. 个
7. 如图,是中的平分线,,交于点,,交于点,若,,则的面积是( )
A. B. C. D.
8. 如图,已知菱形的边长为,点是对角线上的一动点,且,则的最小值是( )
A.
B.
C.
D.
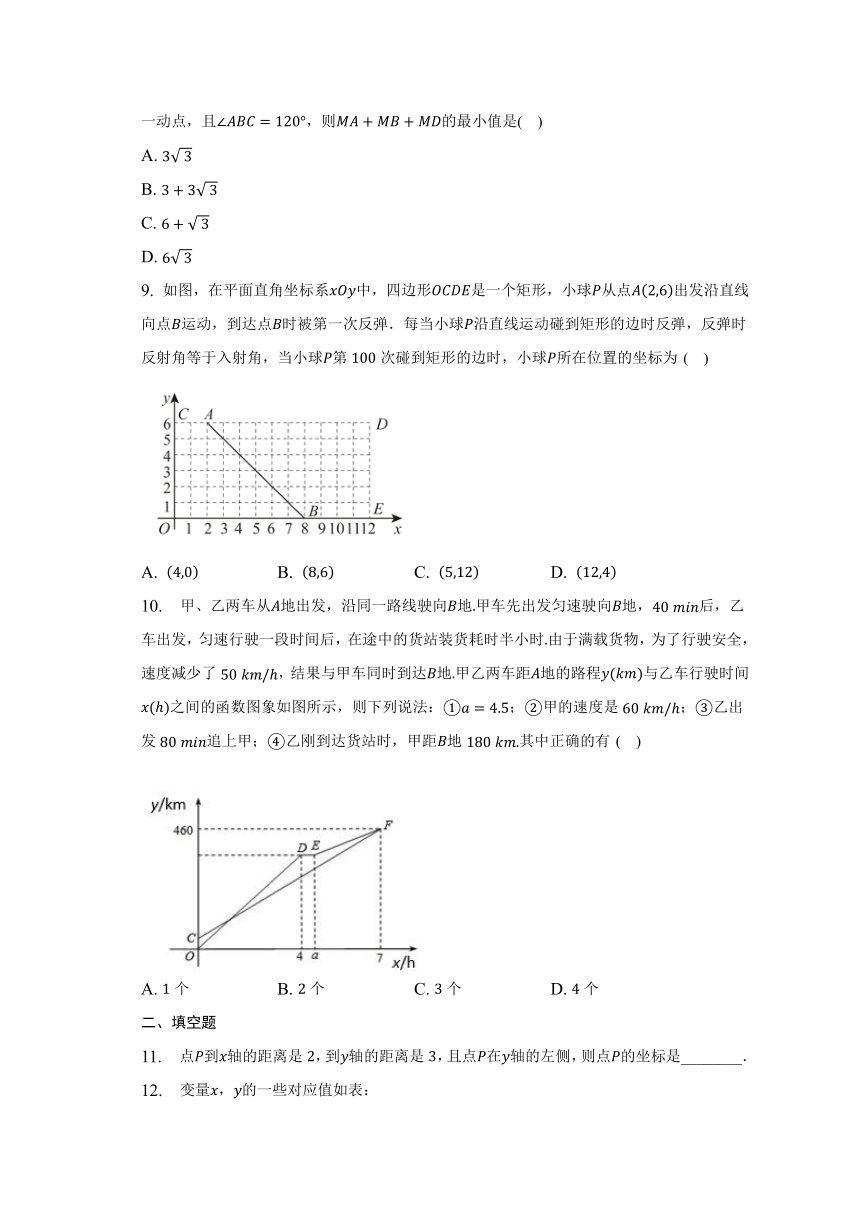
9. 如图,在平面直角坐标系中,四边形是一个矩形,小球从点出发沿直线向点运动,到达点时被第一次反弹.每当小球沿直线运动碰到矩形的边时反弹,反弹时反射角等于入射角,当小球第次碰到矩形的边时,小球所在位置的坐标为( )
A. B. C. D.
10. 甲、乙两车从地出发,沿同一路线驶向地甲车先出发匀速驶向地,后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时由于满载货物,为了行驶安全,速度减少了,结果与甲车同时到达地甲乙两车距地的路程与乙车行驶时间之间的函数图象如图所示,则下列说法:;甲的速度是;乙出发追上甲;乙刚到达货站时,甲距地其中正确的有( )
A. 个 B. 个 C. 个 D. 个
二、填空题
11. 点到轴的距离是,到轴的距离是,且点在轴的左侧,则点的坐标是________.
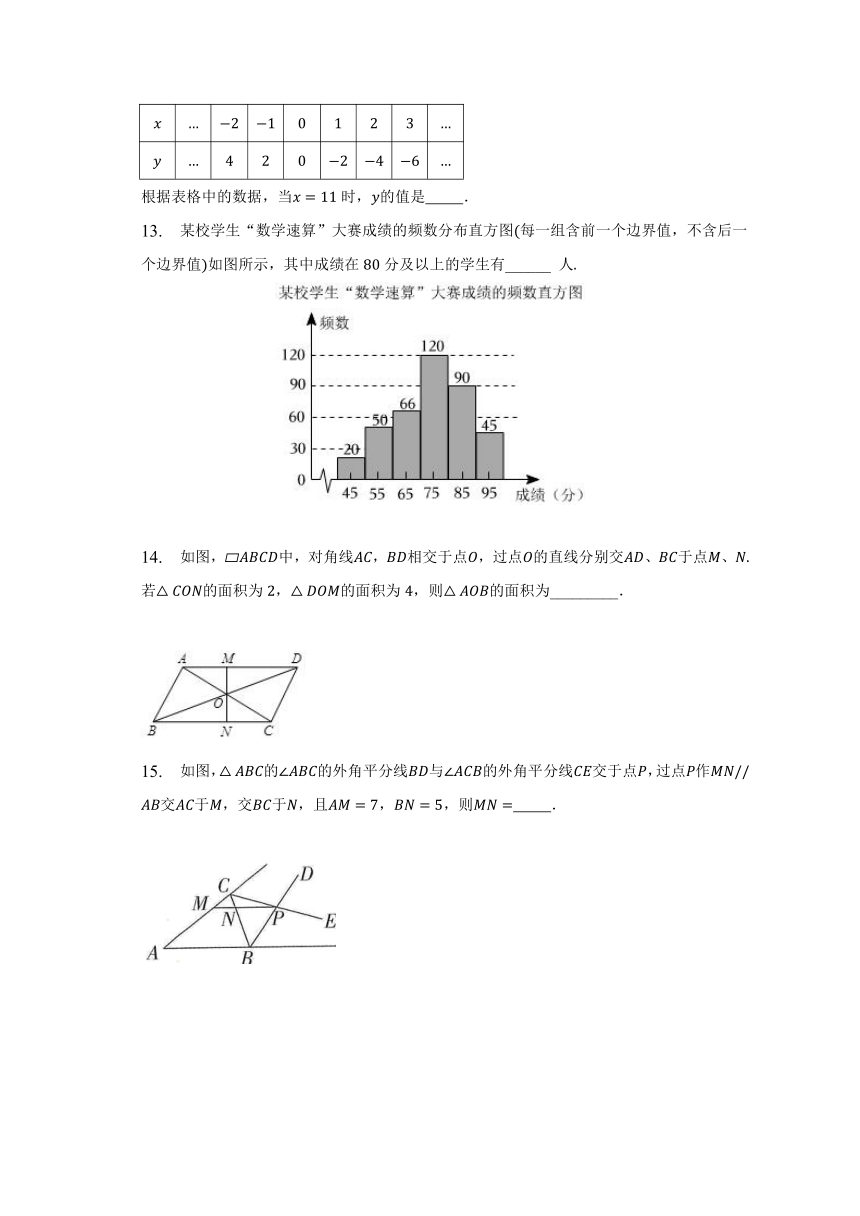
12. 变量,的一些对应值如表:
根据表格中的数据,当时,的值是 .
13. 某校学生“数学速算”大赛成绩的频数分布直方图每一组含前一个边界值,不含后一个边界值如图所示,其中成绩在分及以上的学生有______ 人
14. 如图,中,对角线,相交于点,过点的直线分别交、于点、若的面积为,的面积为,则的面积为_________.
15. 如图,的的外角平分线与的外角平分线交于点,过点作交于,交于,且,,则 .
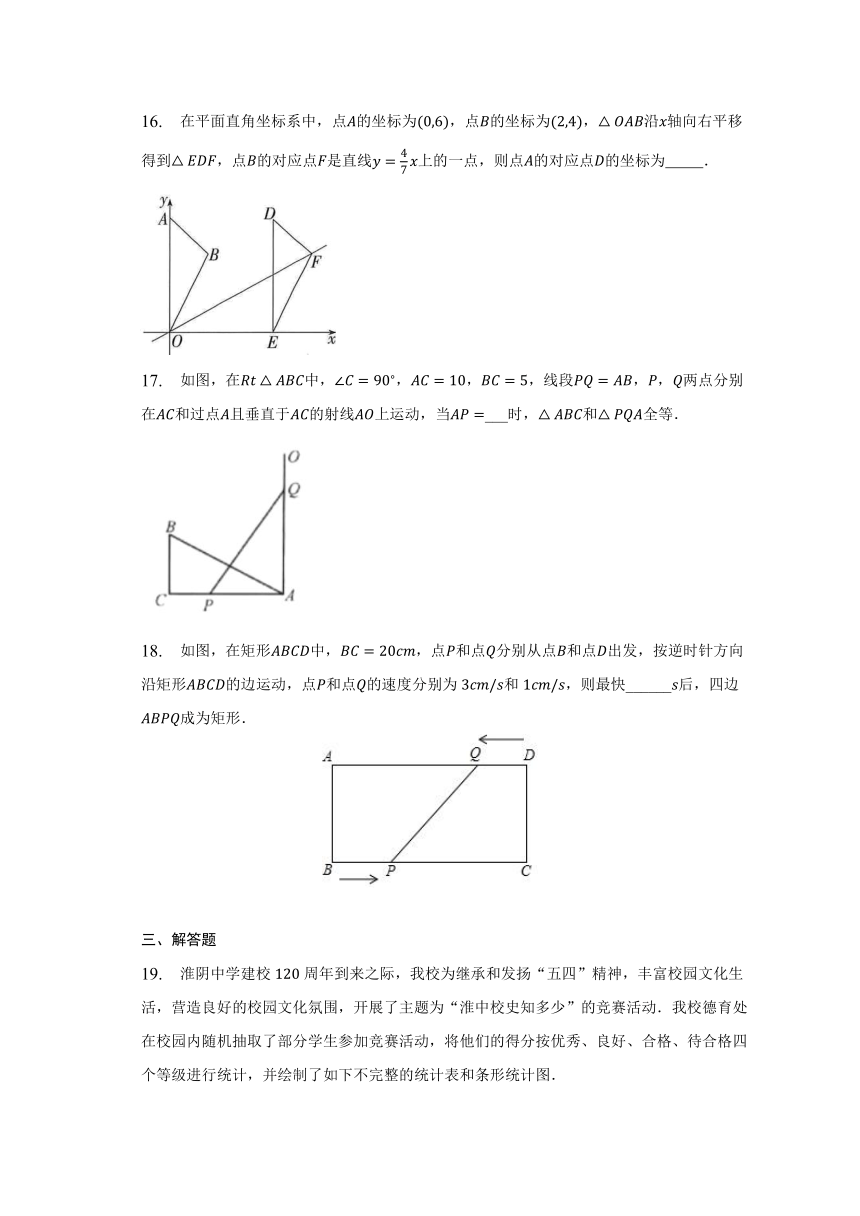
16. 在平面直角坐标系中,点的坐标为,点的坐标为,沿轴向右平移得到,点的对应点是直线上的一点,则点的对应点的坐标为 .
17. 如图,在中,,,,线段,,两点分别在和过点且垂直于的射线上运动,当___时,和全等.
18. 如图,在矩形中,,点和点分别从点和点出发,按逆时针方向沿矩形的边运动,点和点的速度分别为和,则最快______后,四边成为矩形.
三、解答题
19. 淮阴中学建校周年到来之际,我校为继承和发扬“五四”精神,丰富校园文化生活,营造良好的校园文化氛围,开展了主题为“淮中校史知多少”的竞赛活动.我校德育处在校园内随机抽取了部分学生参加竞赛活动,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 频数 频率
优秀
良好
合格
待合格
本次调查随机抽取了______名学生;表中______,______.
补全条形统计图.
若全校共有名学生,请你估计该校掌握校史知识得分等级为“良好”的学生共有多少人.
20. 如图,在平面直角坐标系中,三角形三个顶点的坐标分别为,,.
将三角形向右平移个单位长度,再向上平移个单位长度,得到三角形,其中点,,分别为点,,的对应点.
请在所给坐标系中画出三角形,并直接写出点的坐标;
若边上一点经过上述平移后的对应点为,用含,的式子表示点的坐标;直接写出结果即可
求三角形的面积.
21. 已知:一次函数的图象与轴交于点,与轴交于点.
求一次函数的解析式;
若直线上的有一点,且,求点的坐标.
22. 如图,在四边形中,,,是上一点,交于,连接.
证明:;
若,试证明四边形 是菱形;
在的条件下,试确定 点的位置,使得,并说明理由.
23.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售经了解,每个乙种粽子的进价比每个甲种粽子的进价多元,用元购进甲种粽子的个数与用元购进乙种粽子的个数相同.
甲、乙两种粽子每个的进价分别是多少元?
该超市计划购进这两种粽子共个两种都有,其中甲种粽子的个数不低于乙种粽子个数的倍,若甲、乙两种粽子的售价分别为元个、元个,设购进甲种粽子个,两种粽子全部售完时获得的利润为元.
求与的函数关系式,并求出的取值范围;
超市应如何进货才能获得最大利润,最大利润是多少元?
24. 如图,中,点是边上一个动点,过作直线设交的平分线于点,交的外角平分线于点.
求证:;
若,,求的长;
当点在边上运动到什么位置时,四边形是矩形?并说明理由.
25.
阅读理解.
利用旋转变换解决数学问题是一种常用的方法如图,点是等边三角形内一点,,,,求的度数.
为利用已知条件,不妨把绕点顺时针旋转得到,连接利用这种变换可以求的度数,请写出推理过程.
类比迁移如图,点是等腰内一点,,,,,求的度数.
一、选择题
1. 对于任意的矩形,下列说法一定正确的是( )
A. 对角线垂直且相等 B. 四边都互相垂直
C. 四个角都相等 D. 是轴对称图形,但不是中心对称图形
2. 在平面直角坐标系中,点向右平移个单位长度,得到点,则点的坐标为( )
A. B. C. D.
3. 函数是关于的一次函数,则,的值为( )
A. , B. , C. , D. ,
4. 某校有名学生参加体育测试,其成绩在分之间的有人,则在分之间的频率是( )
A. B. C. D.
5. 将直线向上平移个单位长度后,所得的直线的解析式为( )
A. B. C. D.
6. 下列说法中,正确的有( )
都含有的两个直角三角形一定全等;
都含有的两个等腰三角形一定全等;
底边相等的两个等腰三角形一定全等;
边长都为的两个等边三角形一定全等;
如果两个等腰三角形的腰长相等,且一腰上的高与另一腰的夹角也恰好相等,那么这两个等腰三角形全等.
A. 个 B. 个 C. 个 D. 个
7. 如图,是中的平分线,,交于点,,交于点,若,,则的面积是( )
A. B. C. D.
8. 如图,已知菱形的边长为,点是对角线上的一动点,且,则的最小值是( )
A.
B.
C.
D.
9. 如图,在平面直角坐标系中,四边形是一个矩形,小球从点出发沿直线向点运动,到达点时被第一次反弹.每当小球沿直线运动碰到矩形的边时反弹,反弹时反射角等于入射角,当小球第次碰到矩形的边时,小球所在位置的坐标为( )
A. B. C. D.
10. 甲、乙两车从地出发,沿同一路线驶向地甲车先出发匀速驶向地,后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时由于满载货物,为了行驶安全,速度减少了,结果与甲车同时到达地甲乙两车距地的路程与乙车行驶时间之间的函数图象如图所示,则下列说法:;甲的速度是;乙出发追上甲;乙刚到达货站时,甲距地其中正确的有( )
A. 个 B. 个 C. 个 D. 个
二、填空题
11. 点到轴的距离是,到轴的距离是,且点在轴的左侧,则点的坐标是________.
12. 变量,的一些对应值如表:
根据表格中的数据,当时,的值是 .
13. 某校学生“数学速算”大赛成绩的频数分布直方图每一组含前一个边界值,不含后一个边界值如图所示,其中成绩在分及以上的学生有______ 人
14. 如图,中,对角线,相交于点,过点的直线分别交、于点、若的面积为,的面积为,则的面积为_________.
15. 如图,的的外角平分线与的外角平分线交于点,过点作交于,交于,且,,则 .
16. 在平面直角坐标系中,点的坐标为,点的坐标为,沿轴向右平移得到,点的对应点是直线上的一点,则点的对应点的坐标为 .
17. 如图,在中,,,,线段,,两点分别在和过点且垂直于的射线上运动,当___时,和全等.
18. 如图,在矩形中,,点和点分别从点和点出发,按逆时针方向沿矩形的边运动,点和点的速度分别为和,则最快______后,四边成为矩形.
三、解答题
19. 淮阴中学建校周年到来之际,我校为继承和发扬“五四”精神,丰富校园文化生活,营造良好的校园文化氛围,开展了主题为“淮中校史知多少”的竞赛活动.我校德育处在校园内随机抽取了部分学生参加竞赛活动,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 频数 频率
优秀
良好
合格
待合格
本次调查随机抽取了______名学生;表中______,______.
补全条形统计图.
若全校共有名学生,请你估计该校掌握校史知识得分等级为“良好”的学生共有多少人.
20. 如图,在平面直角坐标系中,三角形三个顶点的坐标分别为,,.
将三角形向右平移个单位长度,再向上平移个单位长度,得到三角形,其中点,,分别为点,,的对应点.
请在所给坐标系中画出三角形,并直接写出点的坐标;
若边上一点经过上述平移后的对应点为,用含,的式子表示点的坐标;直接写出结果即可
求三角形的面积.
21. 已知:一次函数的图象与轴交于点,与轴交于点.
求一次函数的解析式;
若直线上的有一点,且,求点的坐标.
22. 如图,在四边形中,,,是上一点,交于,连接.
证明:;
若,试证明四边形 是菱形;
在的条件下,试确定 点的位置,使得,并说明理由.
23.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售经了解,每个乙种粽子的进价比每个甲种粽子的进价多元,用元购进甲种粽子的个数与用元购进乙种粽子的个数相同.
甲、乙两种粽子每个的进价分别是多少元?
该超市计划购进这两种粽子共个两种都有,其中甲种粽子的个数不低于乙种粽子个数的倍,若甲、乙两种粽子的售价分别为元个、元个,设购进甲种粽子个,两种粽子全部售完时获得的利润为元.
求与的函数关系式,并求出的取值范围;
超市应如何进货才能获得最大利润,最大利润是多少元?
24. 如图,中,点是边上一个动点,过作直线设交的平分线于点,交的外角平分线于点.
求证:;
若,,求的长;
当点在边上运动到什么位置时,四边形是矩形?并说明理由.
25.
阅读理解.
利用旋转变换解决数学问题是一种常用的方法如图,点是等边三角形内一点,,,,求的度数.
为利用已知条件,不妨把绕点顺时针旋转得到,连接利用这种变换可以求的度数,请写出推理过程.
类比迁移如图,点是等腰内一点,,,,,求的度数.
同课章节目录
